Study on compressing principle of the fresh municipal solid waste

2.1. Duncan-Chang $\mathit{E}-\mathit{\mu }$ constitutive model

Until now, domestic and international scholars proposed countless soil constitutive models, and the Duncan-Chang model is one of them. In the conventional triaxial test, the axial stress ${\sigma }_1$ is applied when the ${\sigma }_3$ is unchanged. At this time, the stress increment is applied in only one direction, and the stress increments of the other directions are unchanged. The Duncan-Chang model starts from this point [8]. The model is a nonlinear elastic model based on the incremental generalized Hooke’s law. It can reflect the nonlinearity of the stress-strain relationship with only 8 parameters, and every parameter has clear physical meaning, so it’s easy to grasp. It can be determined by static triaxial test, and is easy to be used in numerical calculation, therefore, it has been used widely [9, 10].

Fig. 1The relation between σ1-σ3 and ε1

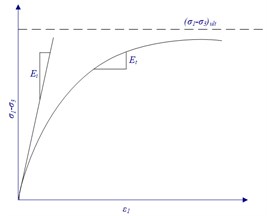
Fig. 2The relation of ε1 and ε3

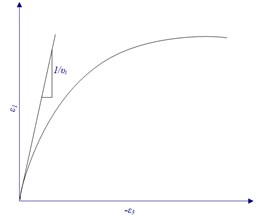
The relationship between ${\sigma }_1-{\sigma }_3$ and axial strain ${\epsilon }_1$ can be represented with a hyperbola, as shown in Fig. 1. The relationship between axial strain ${\epsilon }_1$ and the confined strain ${\epsilon }_3$ can also be represented with a hyperbola, as shown in Fig. 2.

The tangent elastic modulus $E_t$ at any stress $\left({\sigma }_1,{\sigma }_3\right)$ is shown in Eq. (1) [8]:

where, initial tangent elastic modulus $E_i=K{p}_a({\sigma }_3/p_a{)}^n$; $K$ is coefficient of elastic modulus; $n$ is exponent of elastic modulus; $p_a$ is atmospheric pressure; ${\sigma }_3$ is minor principal stress or confining pressure; $c$ is cohesion; $\phi$ is internal friction angle; $R_f$ is damage ratio.

The tangent Poisson’s ratio ${\mu }_t$ at any stress (${\sigma }_1$, ${\sigma }_3$) is shown in Eq. (2):

where, initial Poisson’s ratio ${\mu }_i=G-F\lg ({\sigma }_3/p_a)$, $G$, $F$ and $D$ are the undetermined parameters of the initial Poisson’s ratio.

To summarize, the eight parameters of Duncan-Chang constitutive model are cohesion $c$, internal friction angle $\phi$, damage ratio $R_f$, elastic modulus coefficient $K$, elastic modulus exponent $n$, undetermined parameter of the tangent Poisson’s ratio $G$, $F$ and $D\text{.}$ The Duncan-Chang constitutive model parameters are generally obtained through triaxial tests. But maintaining confining pressure ${\sigma }_3$ in triaxial test device is very difficult and needs lot of auxiliary devices. Meanwhile, almost all scales of triaxial test devices are small, and they are not suitable to conduct garbage compression test due to uneven composition. It’s difficult and costly to develop large scale triaxial test devices. Zhang [5] proposed a simplified calculation method, in which Duncan-Chang model can be put out by the results of direct shearing test and the axial direction compression test.

2.2. Direct shear test

The direct shear test is a common method for determining the shear strength in soil mechanics. The shear stress at the horizontal plane failure can be obtained from horizontal shear force to the samples under different vertical pressures. And cohesion $c$, internal friction angle $\phi$ can be calculated further according to the Coulomb strength theory. According to Zhang’s suggestion [5], we used the slow shear test of the direct shear test, and cohesion $c$, internal friction angle $\phi$ were taken as the parameters of the Duncan-Chang model when the shear strain reached 10 %. The relation between normal stress$\mathrm{}\sigma$ and shear stress ${\tau }_f$ is shown in Coulomb equation Eq. (3):

Taking the shear stress ${\tau }_f$ as ordinate and the normal stress$\mathrm{}\sigma$ as abscissa, the relationship between the shear stress and the normal stress is plotted in Fig. 3. The intercept of the line on the ordinate is cohesion $c$ and the inclination of the line is the internal friction angle $\phi$, as shown in Fig. 3.

Fig. 3Principle of direct shear test

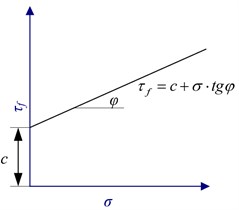
Fig. 4Direct shear test device: a – upper bucket; b – middle bucket; c – lower bucket; d – upper bucket support; e – lower bucket support; f – horizontal slide; g – horizontal slide support; h – horizontal actuator; i – vertical actuator; j – vertical cylinder fixed frame; k – sewage tank

A large-scale test device was needed, so inner diameter of the test device was set to 500 mm. The container of traditional direct shear device is generally composed of two parts, one shear surface, which needs to overcome the friction of the sample and the weight of the counterweight. In order to improve the accuracy of the shear test, the container we designed was divided into three parts: upper, middle and lower parts. The shear force is applied to the middle part to achieve the shear of the sample. The upper and lower buckets were fixed completely, while the middle bucket was connected to the horizontal hydraulic actuator through the horizontal slides. Vertical pressure was provided by the vertical hydraulic actuator and horizontal shear is provided by the horizontal actuator. The fresh MSW has a large water content, and a large amount of sewage was continuously discharged during the compression process. So some holes with diameter of 5 mm were arranged at the bottom of the lower bucket for the sewage discharge to sewage tank. The special direct shear device is shown in Fig. 4.

2.3. Confined compression test device

Take the logarithm of initial elastic modulus $E_i$ on both sides:

Taking $\lg (E_i/p_a)$ as ordinate and $\lg ({\sigma }_3/p_a)$ as abscissa, the line is plotted as Fig. 5(a). Then the intercept is $\lg K$ and the slope is the elastic modulus exponent $n$. This is the method to determine Duncan-Chang model parameters $K$ and $n$ with the triaxial test. According to the initial Poisson’s ratio ${\mu }_i$, taking ${\mu }_i$ as ordinate and $\lg ({\sigma }_3/p_a)$ as abscissa, the line is plotted as shown in Fig. 5(b). Then the intercept is $G$ and the slope is $F$. This is the method to determine Duncan-Chang model parameters $G$ and $F$ with the triaxial test.

Fig. 5Principle of confined compression test

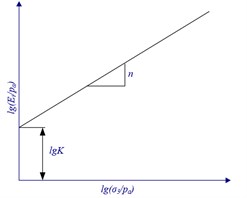
a) The relation between$\mathrm{}\lg (E_i/p_a)$ and $\lg ({\sigma }_3/p_a)$

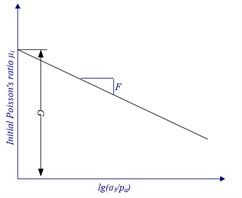
b) the relation between$\mathrm{}{\mu }_i$ and $\lg ({\sigma }_3/p_a)$

Fig. 6Confined compression test device

a) Overall view of the confined test device

b) Strain gauges on outer surface of thin-walled bucket

Confined compression test device was reformed on the basis of the direct shear test device. The upper bucket, middle bucket and lower bucket were kept aligned vertically, and the horizontal actuator was locked. Another thin wall bucket with inner diameter of 476 mm, height of 500 mm and thickness of 2 mm was laid in bucket to conduct the confined compression test, as shown in Fig. 6(a). Seven rows and eight columns of strain gauges were arranged on outer surface of thin wall bucket, and their direction is the circumferential tangential direction, as shown in Fig. 6(b). In the compression process, V402EX wireless dynamic strain test system was used to monitor the microstrain value ${\epsilon }_{\phi }$ of each strain gauge, so that the circumferential tangential stress ${\sigma }_{\phi }$ can be obtained as shown in Eq. (5):

where, $E$ is the elastic modulus of the thin-walled bucket.

Since the wall thickness is much smaller than the radius, the relationship between the circumferential stress ${\sigma }_{\phi }$ and the internal pressure ${\sigma }_3$ of the thin-walled bucket can be obtained according to the elastic mechanics equation Eq. (6):

where, $R$ and $t$ are inner diameter and wall thickness of the thin-walled bucket.

Therefore, the confining pressure ${\sigma }_3$ can be derived as Eq. (7):

In this way, the confining pressure ${\sigma }_3$ of the garbage can be derived by the microstrain values ${\epsilon }_{\phi }$ of these strain gauges.

3.1. Direct shear test data and confined compression test data

The direct shear test data was processed according to Eq. (3), and the points of normal compression stress$\mathrm{}\sigma$ and shear stress ${\tau }_f$ are plotted shown in Fig. 3. The straight line was fitted to obtain the internal friction angle $\phi$ and the cohesion $c$.

The confined test data were processed according to Eq. 4, and the elastic modulus coefficient $K$ and exponent$\mathrm{}n$ were obtained by linear fitting as shown in Fig. 5(a). According to Eq. (4), the data of confined compression test were processed and the coefficient $G$ and $F$ were obtained by linear fitting, as shown in Fig. 5(b).

3.2. The final Duncan-Chang constitutive model parameters

According to Feng’s research [11], the damage ratio $R_f$ of garbage increases with the axial strain. Meanwhile, it is recommended to take $\epsilon =$ 10 % as damage standard of the garbage, and take the damage ratio $R_f=$ 0.55 without triaxial test data. The final Duncan-Chang constitutive model parameters of the fresh MSW were taken the average, as shown in Table 1.

4.1. Model of confined compression test

Based on the Duncan-Chang constitutive model of fresh MSW obtained in the previous article, simulation of garbage compression test was conducted with ANSYS. But all FEA software lacks Duncan-Chang constitutive model, so further development is achieved with the APDL language on ANSYS platform. The material properties of every element are constantly changing in Duncan-Chang constitutive model. According to Duncan-Chang model, the material properties used in the next step need to be calculated with the current stress state.

Simulation of the confined compression test was conducted based on the Duncan-Chang constitutive model in Section 3.2. The inner diameter and height of the thin wall bucket are 476 mm and 500 mm respectively. Axisymmetric model was adopted, and a forced displacement was applied on upper boundary of model, as shown in Fig. 7. Because the stress of garbage is uniform everywhere in the whole model, the garbage can simply be set as one material instead of extracting stress from each element, recalculating its elastic modulus, Poisson's ratio and updating material properties. Therefore, simulation of the confined compression test becomes very simple at this time.

4.2. Analysis results

Analysis terminated due to element excessive distortion, and the final result is shown in Fig. 8, in which the maximum deformation only reached 181 mm. The average pressure curve with the forced displacement of the garbage is shown in Fig. 9. Meanwhile, the average pressure curve with the forced displacement of five tests of the fourth batch is shown in Fig. 9. As shown in the figure, the resistance of the garbage was weak at the early compression stage, and after that, the resistance has sharply increased. The elastic modulus of the garbage changed with average pressure, as shown in Fig. 10.

Fig. 7Test model of waste compression

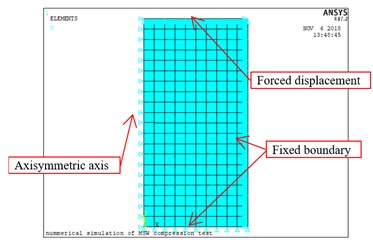
Fig. 8Deformation of last step

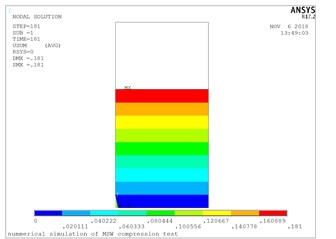
Fig. 9The average pressure along the displacement curve of five tests of the fourth batch and simulation

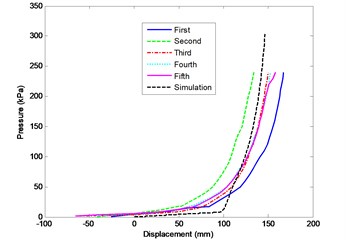
Fig. 10The elastic modulus of the garbage changes with pressure

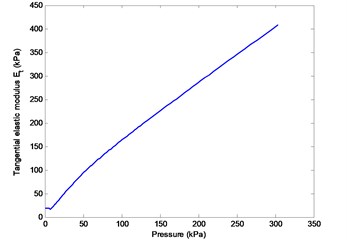
Firstly, geometric nonlinearity and contact nonlinearity were involved. Secondly, it is necessary to extract the principal stress of each element after each loadstep and recalculate and update the elastic modulus and Poisson's ratio according to the Duncan-Chang model. Thirdly, the garbage itself has a large deformation, and it may lead to element malformation and even negative volume, which results in the termination of the calculation. Generally, it is difficult to simulate the whole garbage compression process according to the Duncan-Chang model.