Self-synchronisation of vibration exciters of a biharmonic vibration drive

1. Introduction

As a rule, the efficiency of technological processes increases significantly when using biharmonic laws of vibration of the working body. In such vibrating machines, an inertial four-shaft vibrator with rotors connected by a gear transmission is mainly used as a drive. Such vibrators, in particular, are used in the construction of vibrating conveyors and concentration tables [1, 2]. The latter, according to [1], are quite successfully used in the mining industry. However, kinematic forced synchronisation has a number of significant drawbacks [2].

The problem of self-synchronisation of mechanical vibration exciters remains relevant for vibration engineering. At present, it is quite well studied. The theory and methods for calculating vibration machines with self-synchronising exciters are given in detail in [2, 3]. The vast majority of the results obtained relate to the so-called simple self-synchronisation, when the rotors rotate with the same average angular velocity. The self-synchronisation of vibration exciters rotating at multiple speeds was considered in [2, 4, 5]. In [6], it is demonstrated that self-synchronisation can be used to create vibration machines in which the law of oscillations of the operating part can be changed during operation. In the paper [7], the self-synchronization of four non-ideal exciters is considered via numerical simulation. The investigation result is [8] a verified mathematical model of a vibrating sieve with two self-synchronizing vibration exciters. The paper [9] found that alternate starting of motors can be effective in improving the start-up of vibrating machines with self-synchronising exciters. Paper [10] is devoted to the synthesis of the design parameters of a biharmonic vibrator according to the specified characteristics. In [11], the process of excitation of dual-frequency vibration of a vibrating screen was investigated by computer simulation. In [12], it is shown that self-synchronisation is the vibration capture of the rotation of vibration exciters by the vibrations of a supporting body; that practical problems of self-synchronisation can be solved by the method of studying vibration capture. In the study [13], a vibrating system with five rigid frames driven by four vibrators is proposed to study its synchronization, stability, and self-balance characteristics. Among the recent works devoted to these issues, we note articles [14-17]. In [2], the problem of self-synchronisation of biharmonic vibration exciters on a soft vibration-isolated solid body that oscillates in a plane manner was solved, but a number of important applied issues were left unaddressed. This paper is devoted to the unexplored issues of self-synchronisation of biharmonic drive exciters.

The objective of the study is to demonstrate the practical possibility of self-synchronization of two identical biharmonic vibration exciters installed on a soft vibration-isolated solid body.

2. Dynamic model and equations of motion of the system

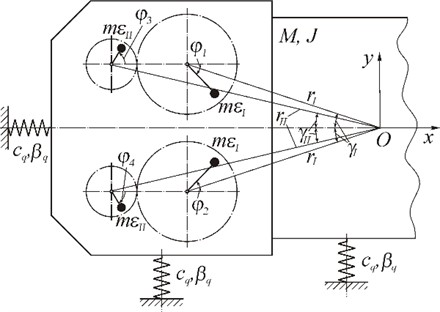
Two unbalanced biharmonic vibration exciters are mounted on a solid body that oscillates in a plane (Fig. 1). The exciters are nominally identical. Each of them consists of two monoharmonic vibration exciters connected by a kinematic (in particular, gear) transmission. The transmission ratio is 1:2. The planes of the exciters are parallel. Vibration exciters with the main rotation frequency are driven by independent asynchronous electric motors rotating in opposite directions. The motion of the system is described by the system of equations [2]:

where:

and $M$, $J$, $q_j=x,y,\phi$ – mass, moment of inertia and generalised coordinates of the supporting body; ${\phi }_s$, $m{\epsilon }_s$ – angles of rotation and static moments of the vibration exciters; $r_s$ – distance from the vibration exciter axis to the centre of gravity $O$; $\beta$ – phase shift angle between vibration exciters rotating at multiple frequencies; $I_{\mathrm{\Sigma }i}$ – reduced moments of inertia of the vibration exciters; $c_q$, ${\beta }_q$ – stiffness and viscous friction coefficients of elastic-damping elements; $L_i\left({\dot{\phi }}_i\right)$ – torque of the electric motor (static characteristic); $R_{\mathrm{\Sigma }i}\left({\dot{\phi }}_i\right)$ – reduced moment of rotational resistance forces (caused mainly by friction in bearings); ${\sigma }_{kt}=\pm 1$ depending on the type of kinematic transmission (for a gear transmission ${\sigma }_{kt}=-1$), $g$ – is the gravitational acceleration.

Fig. 1Diagram of a biharmonic vibration drive

3. Basic equations of vibration mechanics and their analysis

Solutions of Eqs. (1) will be sought by method of direct separation of motions in the form: ${\phi }_i={\sigma }_i[\omega t+{\alpha }_i\left(t\right)+{\psi }_i\left(t,\omega t\right)]$, $q_j=q_j\left(t,\omega t\right)$, where ${\sigma }_i=\pm 1$ – depending on the direction of rotation of the vibration exciter; $\omega$ – the frequency of synchronous rotation; ${\alpha }_i$ – slow, and ${\psi }_i$, $q_j$ – fast $2\pi$ – periodic in terms of $\tau =\omega t$ components, with their average values equal to zero; we also assume that ${\dot{\alpha }}_i\ll \omega$. Following the method used [3, 4], we arrive at the equations of slow and fast motions of the vibration exciters:

where $V_i=⟨{\mathrm{\Psi }}_i⟩$ is the vibration torque, characterizing the vibration connection between vibration exciters. This torque, when the proper conditions are met, leads to self-synchronization.

Note that the angular brackets $⟨⟩$ indicate averaging over $\tau$, while the functions contained in them are calculated at ${\phi }_i={\sigma }_i(\omega t+{\alpha }_i)$; momentum differences $L_i\left({\dot{\phi }}_i\right)-R_{\mathrm{\Sigma }i}\left({\dot{\phi }}_i\right)$, as in [2], are linearised near the synchronous frequency $\omega$; $k_i$ – damping coefficients.

For the case of a soft vibration-isolated supporting body ($c_q\approx 0$), the expression for $V_i$ is obtained as:

where $V_{1\mathrm{m}\mathrm{a}\mathrm{x}}=(m{\epsilon }_I{r}_I\omega {)}^2/2J$, $V_{2\mathrm{m}\mathrm{a}\mathrm{x}}=(m{\epsilon }_{II}{r}_{II}2\omega {)}^2/2J$ are the moduli of partial vibration torques; ${\alpha }_{12}={\alpha }_1-{\alpha }_2$.

Partial vibration torques $V_{j\omega }$ characterise the dynamic coupling between vibration exciters with the same rotational frequencies; the dynamic coupling between vibration exciters with multiple frequencies appears when considering the following approximation. The corresponding vibration torques are relatively insignificant and have no practical interest.

It should be noted that in the case when the exciters with multiple frequencies rotate in the same direction (connected, for example, by a tooth-and-belt transmission), the expression for the vibration torque also takes the form Eq. (3). Consequently, the results below will also hold for these two cases.

Let’s limit ourselves to the case of positive partial frequencies ${\omega }_i$ that do not differ much from each other. From Eq. (3), we obtain the equation for determining the phase shift and frequency in possible synchronous movements (${\alpha }_{12}=const$):

Let the partial velocities of the main vibration exciters be the same. Let us consider the practically important case of synphase rotation of the exciters (${\alpha }_{12}^{\mathrm{*}}=0$). The synphase rotation corresponds to translational biharmonic oscillations of the supporting body along the axis $Ox$. The condition of stability of this mode is reduced to the inequality $d{V}_i/d{\alpha }_i<0$ or $\frac{{\left(m{\epsilon }_I{r}_I\omega \right)}^2}{2J}\left[1+16{\left(\frac{m{\epsilon }_{II}{r}_{II}}{m{\epsilon }_I{r}_I}\right)}^2\right]>0$. This condition is easy to obtain if we use the methodology for studying the vibration capture of the rotation of an unbalanced rotor [12] or if we take into account that the integral stability criterion is valid in the case under consideration [3]. It is important that for a practically interesting resonant case, the synphase mode is stable for any combination of system parameters; that when the condition $m{\epsilon }_I{r}_I>4m{\epsilon }_{II}{r}_{II}$ is met, the mode ${\alpha }_{12}^{*}=0$ will be the only stable mode. According to technological recommendations, usually, $m{\epsilon }_{II}=m{\epsilon }_I/4$. Consequently, the above condition takes the form $r_I>r_{II}$. Thus, for the emergence of the exactly synphase mode of motion, the axes of the vibration exciters with the main rotation frequency should be more distant from the centre of mass of the supporting body than the axes of the “fast” ones. Of course, for a stronger dynamic coupling between the vibration exciters, the distances $r_i$ should be as large as possible, and the torque of inertia of the supporting body should be smaller. However, according to the equations of fast movements of the exciters Eq. (2), an increase in the vibration torque leads to an increase in the speed fluctuations of the exciters.

The condition for the existence of the synphase mode ${\alpha }_{12}^{*}=0$ can be represented as:

or if $m{\epsilon }_{II}=m{\epsilon }_I/4$, $r_{II}\approx r_{II}$:

where $k_{12}=k_1{k}_2/\left(k_1+k_2\right)$.

Thus, it can be stated that, as in the case of monoharmonic exciters, the self-synchronisation of biharmonic exciters will necessarily be established if their partial velocities are sufficiently close and the power of the motors is not overestimated. Condition Eq. (5) is not “stricter” than the well-known condition for the existence of synphase motion of two exciters rotating in opposite directions and mounted on a supporting body with three degrees of freedom [2]. It is known that vibration machines with such a dynamic scheme are widely used in practice.

The coefficient of vibration coupling [2] between biharmonic vibration exciters can be given as follows: $k_{\omega }=\mathrm{1,3}{V}_{1\mathrm{m}\mathrm{a}\mathrm{x}}/L_n$ (case $m{\epsilon }_{II}=m{\epsilon }_I/4$, $r_{II}\approx r_{II}$), $L_n$ – rated torque of the electric motor. Comparing this coefficient with $k_{\omega }$, the one for the above-mentioned scheme [2], we can expect a sufficiently high stability of the synphase rotation of biharmonic exciters. Stable operation of the biharmonic drive in the mode of vibratory maintenance of rotation can also be expected (this mode is effective in the case of electric motors underloaded in steady-state mode). A condition for the possibility of such a mode is the inequality $R_{\mathrm{\Sigma }i}\left(\omega \right)<V_{i\mathrm{m}\mathrm{a}\mathrm{x}}(1+\mathrm{c}\mathrm{o}\mathrm{s}{\alpha }_{12})$.

Note that, according to [2], [18], the expression for the vibration torque in the case of “stuck” motor speed in the resonance zone (the most loaded mode of work) can be given as [3]: $V_i\approx m{\epsilon }_I{\omega }_s^2{A}_x\mathrm{s}\mathrm{i}\mathrm{n}{\gamma }_x/2$, where ${\omega }_s$ is the frequency of “stuck”; $A_x$ is the amplitude of oscillations of the supporting body along the axis $Ox$; ${\gamma }_x$ is the phase shift between the forcing force of the vibration exciter with the fundamental frequency and the oscillations. Hence, the use of biharmonic vibration exciters does not lead to an increase in motor load in the resonance zone (while generating higher vibration intensity compared to monoharmonic exciters).

It should also be noted that the results obtained for the case of the drive of “fast” vibration exciters from independent engines do not differ qualitatively from those given.

4. The computer simulation results

The numerical integration of Eqs. (1) was performed using the dynamic model of an induction motor [18] with the following basic parameters: $M=$108 kg, $J=$1,2 kg⋅m²; ${\beta }_q=$135 kg/s; $c_q=$3,5×10⁴ N/m; $m{\epsilon }_I=$ 0,44 kg⋅m; $I_{\mathrm{\Sigma }i}=$0,008 kg⋅m²; $r_I=$0,76 m; $r_{II}=$0,51 m; ${\gamma }_I=$0,13 rad; ${\gamma }_{II}=$0,11 rad; motors $P_N=$0,18 kW, ${\omega }_s=$157 rad/s.

The simulation results indicate the possibility of stable synphase rotation of biharmonic vibration exciters. The mode is established despite a given small (up to 3 %) difference in the parameters of the vibration exciters and motors, as well as under different initial conditions and system parameters (in particular, ${\phi }_{10}={\phi }_{20}=$0 and 1,57 rad; $\beta =$0 and 1,1 rad; $g=$ 0 and 9,81 m/s²). Self-synchronisation is evidenced by the constancy of the phase difference between the vibration exciters (Fig. 2), the equality of their average speeds, and the repeatability of the trajectory of the centre of mass of the supporting body in the steady-state mode (Fig. 3). When one of the motors ($t=$1,9 s) was turned off, the mode of vibration support of rotation was established (Fig. 2(a)). At the same time, when the condition $r_I<r_{II}$ was met, only the antiphase rotation of the vibration exciters was established (Fig. 2(b); Fig. 3(b)).

It should be noted that the installation of the main and “fast” vibration exciters in antiphase (according to Eq. (3) self-synchronization does not depend on the angle $\beta$) allows to improve the start of the vibration drive, facilitating the initial rise of disbalances, and as a result, the passage of resonance.

Fig. 2Graphs of the difference in phase shift between vibration exciters

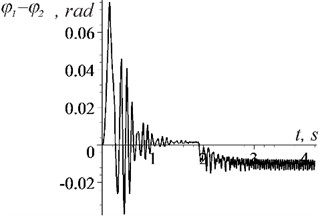
a) Synphase rotation of biharmonic vibration exciters

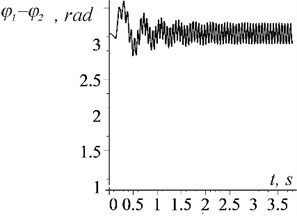
b) Antiphase rotation of biharmonic vibration exciters

Fig. 3Trajectories of the centre of mass of the supporting body

а) $r_I>r_{II}$

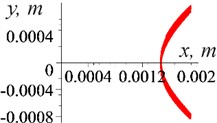
b)$r_I<r_{II}$

5. Conclusions

It is demonstrated that this dynamic scheme provides the possibility of using the phenomenon of self-synchronization of vibration exciters no worse than the scheme with two self-synchronizing unbalanced vibration exciters, widely used at present. At the same time, vibration exciters with multiple speeds can rotate both in the same and opposite directions. For the occurrence of the synphase mode, the axes of the vibration exciters with the main rotation frequency should be more distant from the centre of mass of the supporting body than the axes of the “fast” ones.

The use of self-synchronisation of biharmonic vibration exciters reduces the disadvantages of kinematic synchronisation; expands the possibilities of the drive layout (in particular, allows to reduce the dimensions). In addition, it becomes possible to operate the biharmonic drive in the mode of vibration support of rotation of one of the vibration exciters.