Linear free vibration analysis of rectangular Mindlin plates using coupled displacement field method

1. Introduction

Vibration analysis of plates is an important aspect in the design point of view as the machine parts and air crafts and all mechanical and civil engineering equipment is made up of plates, beams and columns. when these structures subjected to severe loading, deflections may occur in the structures which leads to failure of the structure. To avoid such conditions one must be aware of the natural frequency of the structures. Some of the authors have done research on vibrations of plates with different methods of approach for the past four decades are listed as follows.

Cheung Y. K. and Zhou D., a static Timoshenko beam functions is developed as the admissible functions for the free vibration analysis of Mindlin plates with uniform elastic (translational/rotational) edge constraints by the use of Rayleigh-Ritz method.

Dawe D. J and Roufaeil O. L., applied the Rayleigh-Ritzo method to the prediction of the natural frequencies of the square plates. this analysis is based on the use of Mindlin plate theory vibrations of Mindlin plates by using Ray Leigh-Ritz method.

Eftekhari S. A. and Jafari A. A. analysed the vibrations of plates using High accuracy mixed finite element-Ritz formulation with general boundary conditions. A high order accurate mixed finite element-Ritz method is introduced and developed to study the vibration problem of plates with general boundary conditions. The finite element method (FEM) with higher order interpolation functions is first used to discretize the spatial partial derivatives with respect to a coordinate direction of the plate.

Ferreira A. J. M. studied the Free Vibrations of Timosheko Beams and Mindlin Plates by Radial Basis Functions. A study of free vibration of Timoshenko beams and Mindlin plates is presented whereby the analysis is based on the radial basis function method. Various approaches for computing eigenvalues using radial basis functions are also discussed together with the numerical results for various thickness-to-length ratios.

Han J. B. and Liew K. M., did Static analysis of Mindlin plates using the differential Quadrature element method(DQEM) which is used to solve linear and nonlinear differential equations based on global basis functions.

Kanaka Raju K, et al. studied the effect of non-linearity on the free flexural vibrations of moderately thick rectangular plates. effect of geometric nonlinearity on the free flexural vibrations of moderately thick rectangular plates is studied in this paper. Finite element formulation is employed to obtain the non-linear to linear period ratios for some rectangular plates. A conforming finite element of rectangular shape wherein the effects of shear deformation and rotatory inertia are included, is developed and used for the analysis. Results are presented for both simply supported and clamped boundary conditions.

Lee J. M. and Kim K. C., presented Mindlin Plate Characteristic Functions for the Vibration Analysis of Rectangular Isotropic Thick Plates. An iterative Kantorovich method is presented for the vibration analysis of rectangular isotropic thick plates [Mindlin plate characteristic functions are derived in general forms by the Kantorovich method initially starting with Timoshenko beam functions consistent with the boundary conditions of the plate.

Ma Y. Q. and Ang K. K. studied the Free vibration of Mindlin plates based on the relative displacement plate element. The governing equations of motion of Mindlin plates are reformulated using relative displacement concept rather than the rotational degrees of freedom, which has a good property of representation of the rotary inertia effect. Secondly, based on these formulations, the corresponding stiffness matrix and mass matrix are derived using isoparametric concept and assumed strain method, respectively. the natural frequencies of a circular plate are computed

Roufaeil O. L. and Dawe D. J., described finite strip method for the vibration analysis of rectangular Mindlin plates. A finite strip analysis of vibration of rectangular Mindlin plates with general boundary conditions is described in this method.

Sadrnejad S. A., Saedi Daryan A. and Ziaei M. derived the Vibration Equations of Thick Rectangular Plates Using Mindlin Plate Theory. lateral vibration of thick rectangular plates was studied on the basis of Mindlin plate theory. The exact characteristic equations for a plate which is single supported in two opposite edges are available in the literature. S-C-S-F boundary condition which covers all possible situations is selected in this study.

Sakiyama T. and Matsuda H. studied the Free Vibration of Rectangular Mindlin Plate with Mixed Boundary Conditions by a numerical method in which solutions for differential equations are obtained and converting them in to integral equations to get numerical solutions.

Xiang Y., Lai S. K., Zhou L., used DSC-element method for free vibration analysis of rectangular Mindlin plates. A novel DSC-element method is proposed to investigate the free vibration of moderately thick plates based on the well-known Mindlin first-order shear deformation plate theory. The development of the present approach not only employs the concept of finite element method, but also implements the discrete singular convolution (DSC) delta type wavelet kernel for the transverse vibration analysis. This numerical algorithm is allowed dividing the domain of Mindlin plates into a number of small discrete rectangular elements.

Yufeng Xing and Bo Liu, derived Characteristic Equations and Closed-Form Solutions for Free Vibrations of Rectangular Mindlin Plates. The direct separation of variables is used to obtain the closed-form solutions for the free vibrations of rectangular Mindlin plates. Three different characteristic equations are derived by using three different methods. It is found that the deflection can be expressed by means of the four characteristic roots and the two rotations should be expressed by all the six characteristic roots, which is the particularity of Mindlin plate theory.

Zhou D., a static Timoshenko beam functions is developed as the admissible functions for the free vibration analysis of Mindlin plates with uniform elastic (translational/rotational) edge constraints by the use of Rayleigh-Ritz method.

In the present Coupled displacement field method a rotational displacements are assumed (such that they must satisfy the boundary conditions) in two directions i.e. along length and width, transverse displacements are calculated by substituting the assumed rotational displacements in the coupling equation (which is derived from static equilibrium equation) after finding the transverse displacement $w$, total kinetic energy of plate and total strain energy of the plate are calculated and by applying minimization of potential energy (Lagranzian) principle, non-dimensional fundamental frequency parameter is found.

2. Coupled displacement field method (CDF)

In the current investigation the main objective is to find out the linear fundamental frequency of free un-damped vibration of plates. A simple and efficient coupled displacement field method is developed to study the free vibration behavior of the moderately thick rectangular plates. A single term trigonometric admissible displacement field is assumed for one of the variables. Making use of the coupling equation, the spatial variation for the lateral displacement field is derived in terms of the total rotations.

The coupled displacement field method makes the energy formulation to contain half the number of unknown independent coefficients, in the case of a rectangular plate, contrary to the conventional Rayleigh-Ritz method. The lesser number of undetermined coefficients significantly simplifies the vibration problem. The expressions for the linear fundamental frequency parameter for the all edges simply supported moderately thick rectangular plates are derived.

2.1. Linear vibrations of all edges simply supported rectangular plate

The detailed procedure for the CDF method is discussed in this section for the case of evaluating the fundamental linear frequency parameter of a uniform simply supported moderately thick rectangular plate for which the exact vibration mode shape (for shear flexible plate) for the transverse displacement w is well known. In the CDF method the admissible functions for ${\theta }_x$ and ${\theta }_y$ are assumed in the functional form, noting the similarity between $\partial w/\partial x$, ${\theta }_x$ and $\partial w/\partial y$, ${\theta }_y$ and satisfy the boundary conditions and symmetric conditions for the fundamental mode as:

1

${\theta }_x=\alpha \frac{\pi }{a}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi x}{a}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi y}{b},$

2

${\theta }_y=\alpha \frac{\pi }{b}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi x}{a}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi y}{b},$

3

$\frac{dw}{dx}=-{\theta }_x+\frac{h^2}{3.5}\left[\frac{{\partial }^2{\theta }_x}{\partial x^2}+\nu \frac{{\partial }^2{\theta }_y}{\partial y\partial x}\right]+\frac{h^2}{10}\left[\frac{{\partial }^2{\theta }_x}{\partial y^2}+\frac{{\partial }^2{\theta }_y}{\partial y\partial x}\right],$

4

$\frac{dw}{dy}=-{\theta }_y+\frac{h^2}{3.5}\left[\frac{{\partial }^2{\theta }_y}{\partial y^2}+\nu \frac{{\partial }^2{\theta }_x}{\partial y\partial x}\right]+\frac{h^2}{10}\left[\frac{{\partial }^2{\theta }_y}{\partial x^2}+\frac{{\partial }^2{\theta }_x}{\partial y\partial x}\right].$

Fig. 1Rectangular plate (a/b= 2) of length “a”, width “b” and thickness “h”

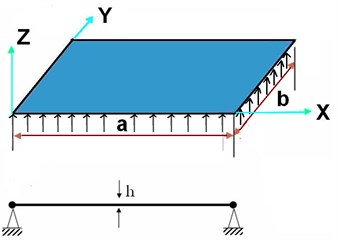
Fig. 2All edges simply supported rectangular plate

Substituting Eqs. (1) and (2) in Eqs. (3) and (4) and after simplification and substituting $a/b=$ 2 as:

5

$\frac{dw}{dx}=-\alpha \frac{\pi x}{2b}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi x}{2b}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi y}{b}\left(1+3.5246{\left(\frac{h}{b}\right)}^2\right),$

6

$\frac{dw}{dy}=-\alpha \frac{\pi x}{2b}\mathrm{c}\mathrm{o}\mathrm{s}\frac{\pi x}{2b}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi y}{b}\left(1+3.5246{\left(\frac{h}{b}\right)}^2\right).$

Integration of Eq. (5) and after evaluation of the constant of integration:

7

$w=-\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi x}{2b}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi y}{b}\left[\left(1+3.5246{\left(\frac{h}{b}\right)}^2\right)\alpha \right].$

2.2. Total Strain energy ($\mathit{U}$) developed in the plate:

2.2.1. The strain energy stored due to bending moment in the plate

If a plate is bent by uniformly distributed bending moments $M_x$ and $M_y$ so that a moment, see below figure, so that $xz$ and $yz$ planes are the principle planes of the deflection surface of the plate, the strain energy stored in the element is obtained by calculating the work done by the moments $M_{x}dy$ and $M_{y}dx$ on the element during the bending of the plate.

2.2.2. The strain energy stored due to transverse shear force

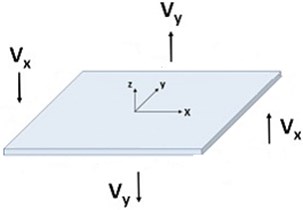
The transverse shear force $V_x$ is acting on the $xy$ plane may cause the displacement in the plate which will lead to strain energy.

The total strain energy is the combination of the strain energies due to bending moment and transverse shear force in the plate.

Total strain energy = Strain energy due to bending moment + Strain energy due to transverse shear force:

8

$U=\frac{D}{2}\underset{0}{\overset{a}{\int }}\underset{0}{\overset{b}{\int }}‍\left\{{\left(\frac{\partial {\theta }_x}{\partial x}\right)}^2+{\left(\frac{\partial {\theta }_y}{\partial y}\right)}^2+2\nu \frac{\partial {\theta }_x}{\partial x}\frac{\partial {\theta }_y}{\partial y}+2\left(1-\nu \right)\frac{\partial {\theta }_x}{\partial y}\frac{\partial {\theta }_y}{\partial x}\right\}dxdy$
$+\frac{kGh}{2}\underset{0}{\overset{a}{\int }}\underset{0}{\overset{b}{\int }}‍\left\{{\left(\frac{dw}{dx}+{\theta }_x\right)}^2+{\left(\frac{dw}{dy}+{\theta }_y\right)}^2\right\}dxdy,$

where $k$ is shear correction factor is 5/6 and $\nu$ is Poisson’s ratio is 0.3.

Substituting Eqs. (1) and (2) and Eqs. (5) and (6) in Eq. (8) and after simplification as:

9

$U=\frac{D{\pi }^4}{4b^2}\left\{\left(1.5625+5.5071{\left(\frac{h}{b}\right)}^2\right){\alpha }^2\right\}.$

Fig. 3Bending moment in the plate

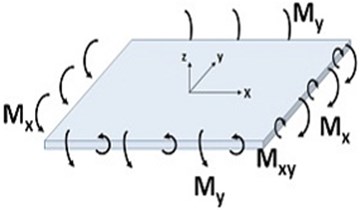
Fig. 4Transverse shear force in the plate

2.2.3. Total kinetic energy ($\mathit{T}$)

The kinetic energy in the plate is the combination of the KE due to transverse displacement and KE due to rotations. The plate displaced through a distance of $w$ will give the kinetic energy given as:

10

$T=\frac{\rho h{w}_L^2}{2}\underset{0}{\overset{a}{\int }}\underset{0}{\overset{b}{\int }}{w}^{2}dxdy.$

Similarly, for the rotations ${\theta }_x$ and ${\theta }_y$, the kinetic energy developed in the plate will be:

11

$T=\frac{\rho h{w}_L^2}{2}\underset{0}{\overset{a}{\int }}\underset{0}{\overset{b}{\int }}\left[\frac{h^2}{12}\left({\theta }_x^2+{\theta }_y^2\right)\right]dxdy.$

Therefore, the expression for kinetic energy of plate is given as:

12

$T=\frac{\rho h{w}_L^2}{2}\underset{0}{\overset{a}{\int }}\underset{0}{\overset{b}{\int }}\left[w^2+\frac{h^2}{12}\left({\theta }_x^2+{\theta }_y^2\right)\right]dxdy.$

Substituting Eqs. (1) and (2) and Eq. (7) in Eq. (12) and after simplification:

13

$T=\rho h{\omega }_L^2{b}^2\left\{\left(0.25+2.0191{\left(\frac{h}{b}\right)}^2+3.1055{\left(\frac{h}{b}\right)}^4\right){\alpha }^2\right\}.$

By minimizing the Lagrangian with respect to undetermined coefficient $\alpha$:

14

$\frac{\partial \left(U-T\right)}{\partial \alpha }=0.$

The fundamental frequency parameter will be:

15

$\lambda =\frac{\rho h{\omega }_L^2{b}^4}{D}=\frac{\frac{25{\pi }^4}{16}\left(1+3.5246{\left(\frac{h}{b}\right)}^2\right)}{1+8.0764{\left(\frac{h}{b}\right)}^2+12.422{\left(\frac{h}{b}\right)}^4}.$

3. Numerical results and discussion

The concept of Coupled displacement field method is used to determine the fundamental frequencies of rectangular thick plates with most practically used simply supported boundary condition. The numerical results are obtained in terms of fundamental frequency parameter ($\lambda$) and thickness to width ration $\left(h/b\right)$.

Table 1 shows the variation of fundamental frequency parameter values with variation of thickness to width ratio. trigonometric admissible function. For the sake of comparison and validation of the proposed method, the results obtained by present coupled displacement method are compared with Kanaka Raju K. et al. are also included in this table. The value obtained for non-dimensional fundamental frequency parameter for the given rectangular thick plate beam is exactly matching with the Reference values.

4. Conclusions

In this paper the coupled displacement method is used to evaluate the vibration behavior of rectangular Mindlin plates with simply supported beam boundary condition. This method is having very less complexity when compared to other energy method like Rayleigh-Ritz method. The coupled displacement field method makes the energy formulation to contain half the number of unknown independent coefficients, in the case of a rectangular plate, contrary to the conventional Rayleigh-Ritz method. The lesser number of undetermined coefficients significantly simplifies the vibration problem. The expressions for the linear fundamental frequency parameter values for the all edges simply supported thick rectangular plates are derived. The numerical results obtained from the present formulation are in very good agreement with those obtained from the existing Literature.