Bluff body flow at different Reynolds numbers based on Lattice-Boltzmann method

1. Introduction

The flow around a bluff body [1] exists widely in the field of construction, transportation and other research because the fluid will produce a large range of separation on the surface of bluff body and form a broad wake with vortex shedding phenomenon, which makes it complex to simulate the turbulent field around bluff body with a simple geometric boundary [2]. In recent years, the lattice Boltzmann method has become a new numerical simulation method, which is suitable for simulating the flow around bluff body. The key of lattice Boltzmann method is to determine the fluid motion distribution function and boundary conditions.

The solution of viscous fluid is not only related to the boundary conditions, but also to the Reynolds number. The smaller the Reynolds number is, the more significant the influence of viscous force is. While the bigger the Reynolds number is, the more significant the influence of inertia force is. When Reynolds number [3, 4] is small, viscous effects are important in the whole flow field. On the contrary, when Reynolds number is high, the effect of fluid viscosity on the flow around a body is important only in the wake of the boundary layer and the rear end of the object. When inertia force and viscous force play an important role in the flow, in order to make the two flow fields with similar geometric satisfy the similar dynamic conditions, the equal Reynolds number of the model and the object must be guaranteed. Therefore, in this paper, we simulate flow around a square cylinder at different Reynolds numbers based on lattice Boltzmann method and demonstrate that BGK-LBM is suitable for flow simulation around bluff body with small Reynolds number.

2. Reynolds number

In 1883, Reynolds observed the flow of fluid in a circular tube [5]. Then firstly he pointed out that the flow pattern was related to three factors including the diameter of the tube, the viscosity of the fluid and the density of the fluid. Reynolds number ($Re$) indicates the similarity criterion of the viscous effect in fluid mechanics $f_i\left(x+c_i\mathrm{\Delta }t,t+\mathrm{\Delta }t\right)-f_i\left(x,t\right)=-\left[f_i\left(x,t\right)-f_i^{eq}\left(x,t\right)\right]/\tau$,

where $\tau$ and $c_i$ are fluid density and kinematic viscosity coefficient respectively, $f_i$ and $f_i^{eq}$ are characteristic velocity and characteristic length of flow field respectively. Re is physically expressed as the ratio of inertia force and viscous force. As for outflow problem, $f_i$ and $f_i^{eq}$ are decided on stream velocity far ahead and main dimensions of objects. But as for inner flow problem, they are determined by the average velocity and the diameter of the tube. When the $Re$ of two geometrically similar flow field is equal, the ratio of the inertia force and viscous force is equal.

When Re is small, the effect of viscous force on the flow field is larger than that of inertia force. The disturbance of flow velocity in flow field will decrease due to viscous force resulting that the fluid flow is stable in the form of laminar flow. Conversely, when $Re$ is high [6], the effect of inertia force on the flow field is larger than that of viscous force. And the fluid flow is somehow unstable. The micro change of the flow velocity is easy to develop and strengthen. It’s also easy to form a disordered and irregular turbulent flow field.

3. The Lattice Boltzmann method

The Lattice Boltzmann method [7-9] (LBM) is one of the most important achievements in recent 20 years of computational fluid mechanics and different from the traditional numerical methods [6] for fluid calculation and modeling method describing the movement of the molecule. LBM regards the fluid as discrete system composed of a large number of mesoscopic particle. According to the movement characteristics of the particle, a simplified LB equation is established to calculate the evolution of particle distribution function.

LBE [11] is an integro-partial differential equation, so one of the difficulties in solving LBE is the complexity of the collision integral. In order to simplify the solving process, a collision function model with a simple operator instead of collision was proposed by Bhatnagar, Gross and Krook in 1954. LBE is a special discrete form of Boltzmann-BGK equation including discrete velocity, discrete time and space discretization.

The lattice Boltzmann evolution equation of the single relaxation time is:

where $\tau$, $c_i$, $f_i$, $f_i^{eq}$ are the relaxation factor, discrete velocity, particle distribution function and equilibrium distribution function respectively.

In 1992, professors including Qian proposed the model DnQb [11] n and b refer to space dimension and discrete velocity respectively) and the equilibrium distribution function is:

where $c_s$ is sound velocity of the grid and ${\omega }_i$ is weight coefficient. The two parameters decide that the rage of lattices depends on the selecting of $c_i$in discrete velocity model.

In this paper, we adopted D2Q9 model (shown as Fig. 1).

Fig. 1D2Q9 model

$\left(\mathrm{0,0}\right)c$, $i=0$:

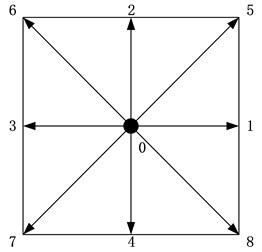
Weight coefficient and sound velocity of lattices are as follows:

In the formula, $c=\mathrm{\Delta }x/\mathrm{\Delta }t$is velocity of grid. $\mathrm{\Delta }x$ and $\mathrm{\Delta }t$ are grid length and time step respectively.

The macroscopic velocity and momentum of fluid are:

The relationship between the fluid viscosity coefficient and the relaxation factor of the model is:

Generally, the calculation process of LBE is as follows:

(1) Initialize the distribution function:

(2) Perform collision at $t$:

(3) Perform migration:

(4) Calculate macroscopic thermodynamic quantities:

Repeat steps (2)-(4) until the terminal conditions are met.

In LBM, the accurate simulation of boundary conditions [12-14] is an important and crucial problem, because the boundary conditions are not easy to determine, which needs to confirm the distribution function of the boundary. At present, the types of boundary of LBM can be divided into heuristic schemes, dynamic schemes and interpolation/extrapolation schemes. According to the type of boundary condition, it also can be divided into the velocity boundary and the pressure boundary. Additionally, there are some special artificial boundaries, such as the entrance, exit, infinity, symmetry, etc.

4. Flow simulation around a square cylinder at different Reynolds number

The solution of viscous fluid is not only related to the boundary conditions, but also to $Re$. We choose a rectangle with 400 meters’ length and 45 meters’ width as the computational domain. We suppose the wind velocity is 5 m/s and the Reynolds number is 20. We chose the standard rebounded scheme as the surface free slip boundary and dealt with the flow inlet velocity boundary and the exit constant pressure boundary by the non-equilibrium rebounded scheme. As follows, we selected different $Re$ to simulate the flow.

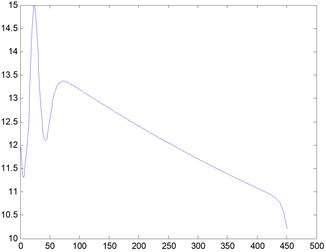
1) $Re=$ 20. The barrier is a rectangular cylinder [15] of 5 m×5 m placed at 20 meters’ away from the entrance. When the Reynolds number is 20, we obtain the streamline, three-dimensional graph and curve graph of maximum speed in a line by use of the MATLAB after 40000 steps of the calculation, as shown in Figs. 2-4.

Fig. 2Streamline, Re= 20

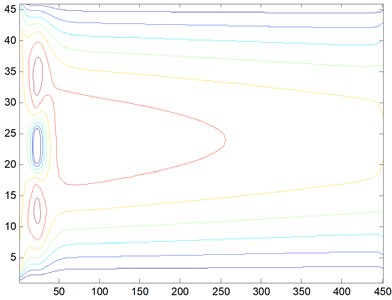
Fig. 33D graph, Re= 20

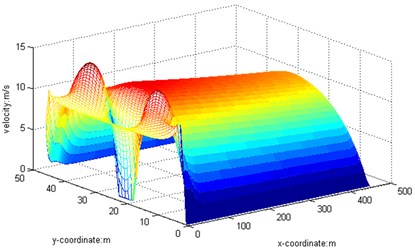
Fig. 4Curve graph, Re= 20

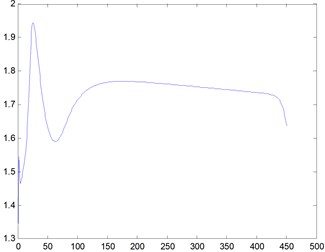
2) $Re=$ 100. The barrier is a rectangular cylinderof 5 m×5 m placed at 20 meters’ away from the entrance. When the Reynolds number is 100, we obtain the streamline, three-dimensional graph and curve graph of maximum speed in a line by use of the MATLAB after 40000 steps of the calculation, as shown in Figs. 5-7.

Fig. 5Streamline, Re= 100

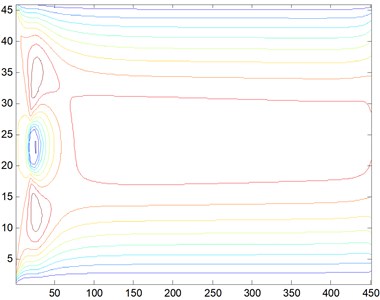
Fig. 63D graph, Re= 100

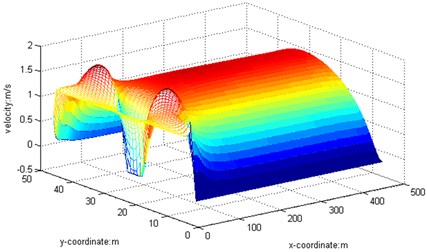
Fig. 7Curve graph, Re= 100

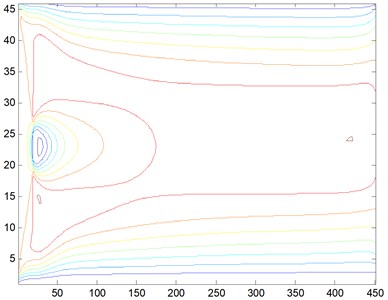
3) $Re=$500. The barrier is a rectangular cylinderof 5 m×5 m placed at 20 meters’ away from the entrance. When the Reynolds number is 500, we obtain the streamline, three-dimensional graph and curve graph of maximum speed in a line by use of the MATLAB after 40000 steps of the calculation, as shown in Figs. 8-10.

Fig. 8Streamline, Re= 500

4) $Re=$1000. The barrier is a rectangular cylinderof 5 m×5 m placed at 20 meters’ away from the entrance. When the Reynolds number is 1000, we obtain the streamline, three-dimensional graph and curve graph of maximum speed in a line by use of the MATLAB after 40000 steps of the calculation, as shown in Figs. 11-13.

Fig. 93D graph, Re= 500

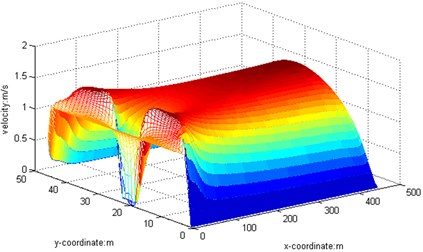
Fig. 10Curve graph, Re= 500

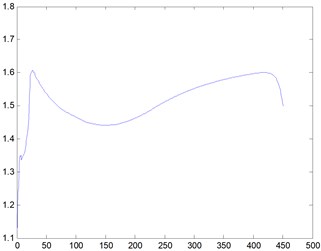
Fig. 11Streamline, Re= 1000

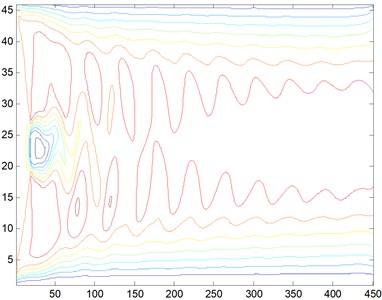
Fig. 123D graph, Re= 1000

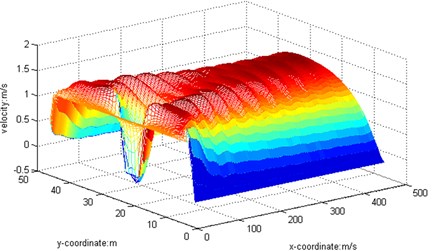
Fig. 13Curve graph, Re= 1000

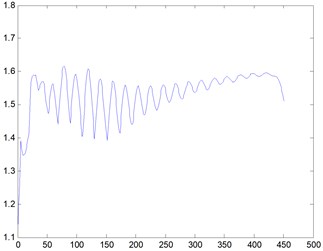
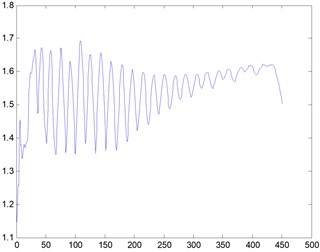
5) $Re=$2000. The barrier is a rectangular cylinderof 5 m×5 m placed at 20 meters’ away from the entrance. When the Reynolds number is 2000, we obtain the streamline, three-dimensional graph and curve graph of maximum speed in a line by use of the MATLAB after 40000 steps of the calculation, as shown in Figs. 14-16.

We can see from the flow around the wake that the variation of the flow field is obvious, and it will gradually tend to be stable after the obstacles. According to Figs. 2-16, we can see that when Re is small, the air velocity of the flow field around the obstacle is larger and it will gradually tend to be stable after the obstacle. However, when Re reaches 1000, apart from big ups and downs of air velocity around the obstacle, the air velocity in flow field after the obstacle is still showing a wave of instability.

Fig. 14Streamline, Re= 2000

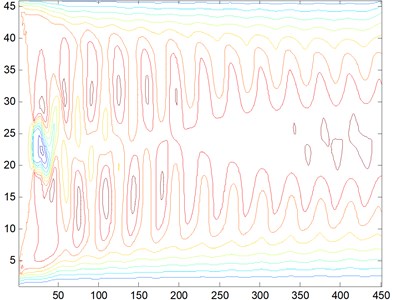
Fig. 153D graph, Re= 2000

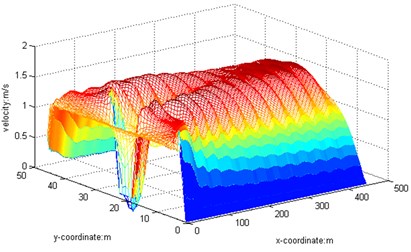
Fig. 16Curve graph, Re= 2000

5. Conclusion

The flow around a bluff body is a classical problem in the field of fluid mechanics. Due to the accuracy of the existing numerical simulation method is low, in this paper; we put forward a numerical simulation method with high accuracy and good stability based on molecular dynamic theory. By using MATLAB to compile calculation program, we carried out the numerical simulation of flow around a square cylinder at different Re and we obtain the streamline, three-dimensional graph and curve graph of maximum speed in a line to study the characteristics of flow around a bluff body. Through the analysis, the following conclusions are drawn: under the conditions of small Re, the variation of flow field around the bluff body is more obvious and it will gradually tend to be stable, which is consistent with the actual theory. With the increase of Re, the air velocity in flow field after the obstacle is still showing a wave of instability. Therefore, BGK-LBM is suitable for the flow simulation of bluff body under small Reynolds numbers.