Numerical simulation of vortex induced vibrations on a circular cylinder at different Reynold’s number

1. Introduction

The flow past circular cylinder is gaining attention of researchers due to its primitive significance in the engineering applications. Steady flow past a circular cylinder gives the various flow regimes at different Reynolds numbers and coefficient of drag rely upon the Reynolds number [1].

In his research, Xiong elaborates that Vortex induced vibrations generates when a structure is placed normally to the direction of flow in a Newtonian fluid so that it can fluctuate due to separation in vortices shedding and both natural and shedding frequency becomes equal [2].

Vortex shedding can successfully lead to separation of delay, drag reduction, and reduction of vibration and noise. There are many features which results from the interactions between the external disturbance, and the flow around the circular cylinder.

Vortex shedding is an oscillating flow of a fluid like air, and water around the bluff bodies at Reynold’s number based on the characteristic length of the body. On the bluff bodies, the flow separation takes place to causes the pressure difference on different surface of the body. The vortices detach from the body periodically producing the Von-Karman street. Results computed from the experimental studies are most reliable, but due to the cost limitations, nowadays numerical methods are more preferred as they also provide reliable, and acceptable results [3].

Fluid passing through the model separates the flow at one or more than one sharp corner and makes the contours and as the Reynolds number increases the substantial difficulties starts occurring [4].

By using laminar separation bubble, and turbulent model, an increase in a Reynolds number we found that there is a rapid reduction in drag force and increases in lift force [5].

By doing experiment on a circular cylinder the investigation of vortex induced vibrations with Low damping ratio gives the idea that there is a change in velocity [6].

To do the computational simulation first order SAS-SST turbulent model has been used on a 2-D cylinder near different wake regions and found that shape of mean velocity is related to fluctuation in velocities [7].

In this paper, we consider the case of flow past a circular cylinder at different Reynolds number. Our research work includes the computational work. The simulations carried out for 2-D Circular Cylinder only. Thus, the present work deals with the lift and drag coefficient in comparison to increase in Reynolds number.

2. Governing equations

Two major governing equations for 2-D incompressible turbulent laminar flow we have used.

Continuity equation is given in Eq. (1):

Navier stokes equations are given in Eq. (2) and Eq. (3).

For $X$-direction component:

For $Y$-direction component:

where $\rho$ is the density, $U$ is the free stream velocity, $p$ is the pressure, $\mu$ is the dynamic viscosity of fluid, $u$ and $v$ are the velocities in $x$ and $y$ directions respectively.

3. 3.Computational domain and meshing

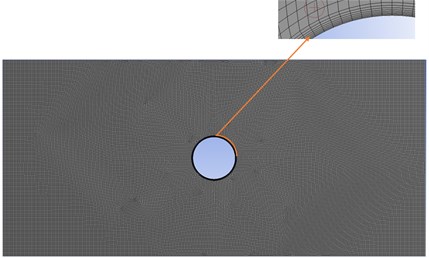
The numerical computation of drag and lift coefficient for different Reynold’s number is studied using Ansys Fluent 19.1. The 2-D cylinder of diameter 5 mm is formed and computational domain is created around it having dimensions of 150 mm×70 mm. The fluid domain with boundary conditions is given in Fig. 1. The inlet is assigned as velocity inlet and outlet is having atmospheric pressure i.e. 101325 Pa and all other walls are having no slip condition. The structured 2-D quadrilateral mesh is used for the domain and inflation layers are formed around the cylinder. The mesh with inflation layers is shown in Fig. 2.

The steady pressure-based solver is used to study the aerodynamic effects around the cylinder. The turbulence model used is standard $k$-$\epsilon$ and SIMPLE scheme is used for pressure and velocity coupling with second order upwind for momentum.

Fig. 1Domain around the cylinder

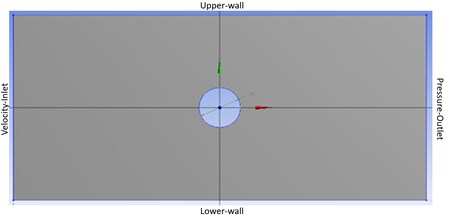
Fig. 2Meshing around the cylinder with inflation layers

4. Results and discussion

The numerical simulation around cylinder is carried out by varying the velocity at inlet to get different Reynold’s number and to analyze the change in lift, drag and pressure coefficient with respect to $Re$. Table 1 shows the drag coefficient and lift coefficient values for different Reynold’s number. The plot for the averaged $C_d$ and $C_l$ along the increasing $Re$ is shown in Fig. 3 and Fig. 4 respectively. It is observed that the drag coefficient decreases on increasing the $Re$ while lift coefficient increases up to $Re=$ 10⁴ and drops for higher $Re$.

Fig. 3Coeffcient of drag vs Reynold’s number

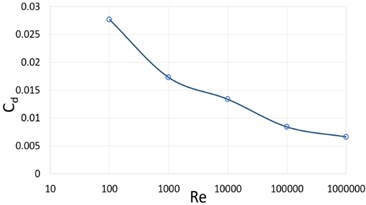
Fig. 4Coeffcient of lift vs Reynold’s number

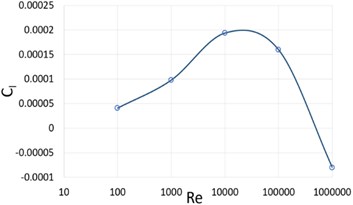
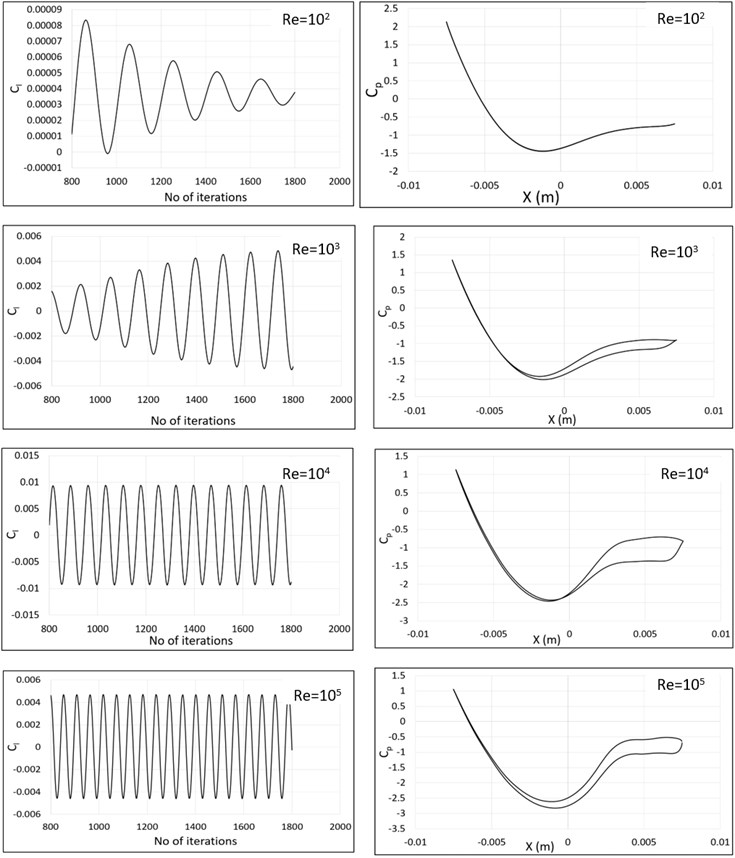
Fig. 5 represents the coefficient of lift and pressure distribution on fixed cylinder for at $Re=$10² ,10³ ,10⁴ and 10⁵. The $C_l$ is plotted for the iteration ranging from 800 to 1800. The $C_l$ value increasing as $Re$ increases till 10⁴ while decreases for further higher values which can be seen from the graph. The value of pressure coefficient is having overlapped curve for at $Re=$10² and the difference between pressure distribution increases along the increasing $Re$.

Fig. 5The lift coefficient and pressure coefficient distribution along the fixed cylinder wall at different Reynold’s number

The vorticity contour is plotted in Fig. 6 to check the wake pattern on the cylinder for increasing $Re$. The range of vortex shedding is kept from –10⁴ to 10⁴. The oscillations around the cylinder increases with Reynold’s number forming von Karman street around the cylinder. It can be seen that separate shear layers are rolling on the upper and lower wall of fixed cylinder. The red color in the vorticity contour represents the clockwise rotation while blue color represents the counterclockwise rotation of vortices.

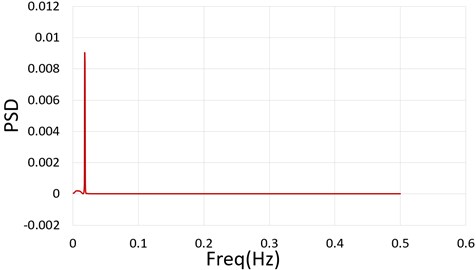
To understand the oscillations around the cylinder due to formation of vortex shedding the power spectral density of the lift coefficient is determined using Fast Fourier Transformation. The maximum frequency for the $Re=$ 10⁵ using FFT is 0.018 Hz. Fig. 7 represents the power spectral distribution for the same.

Fig. 6Velocity contours at different Reynolds numbers

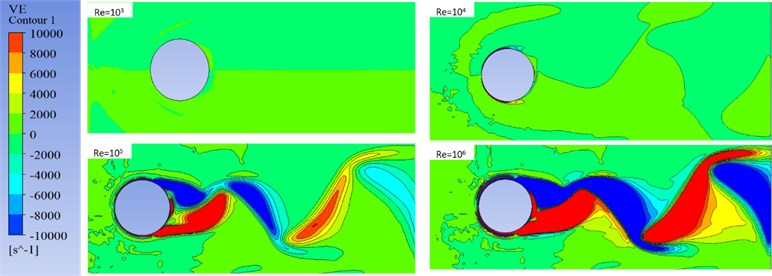
Fig. 7Power spectral distribution vs frequency

5. Conclusions

In this paper the numerical computation for the lift and drag coefficient with increasing number of Reynold’s number is represented. The drag coefficient reduces with the increasing $Re$ and lift coefficient increases up to Reynold’s number 10⁴. Similarly, the pressure difference on the fixed cylinder increases with the increasing Reynold’s number. The vorticity contour and power spectral distribution of lift coefficient is also presented in the results and discussion section.