Numerical analysis of underwater flow past columnar projectile with different cross-sections at high Reynolds numbers

2.1. Description of the test case and models

Hypothesis: Actually, the projectile is moving in the underwater trajectory, and the water fluid medium is stationary. In this paper, to study the flow around the projectile, the projectile is stationary and the water medium fluid is given the relative velocity $u_0$. As shown in Fig. 1, based on quantities of simulation explorations and the Refs. [4-17], the calculation flow field and the relative position of the cylinder are established. The coordinate origin is located at the outer circle center of the cross-section. The excircle diameter of these cross-sections both are $D=$100 mm. Initially, the direction of flow velocity $u_0$ is in the positive direction of the $x$-axis. Also, the velocity component of the fluid in the $x$-axis direction is defined as $u_x$, and the velocity component in the $y$-axis is $u_y$. The flow field is 40$D$×16$D$, and the upstream flow area is 8$D$×16$D$. In order to observe the morphology of the vortex shedding, downstream flow area is 32$D$×16$D$. The distance from the origin to the upper and lower boundaries is 8$D$, so that the influence of the upper and lower wall boundary on the calculation results can be ignored.

Fig. 1The sketch map of flow field in numerical simulation

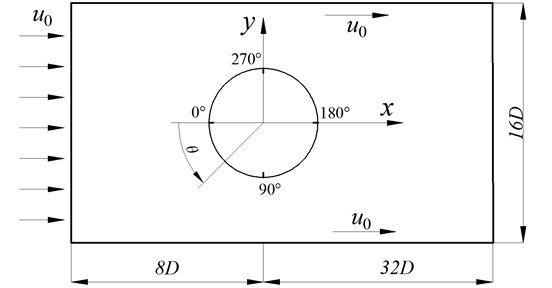
Fig. 2Relative position of prisms in flow field

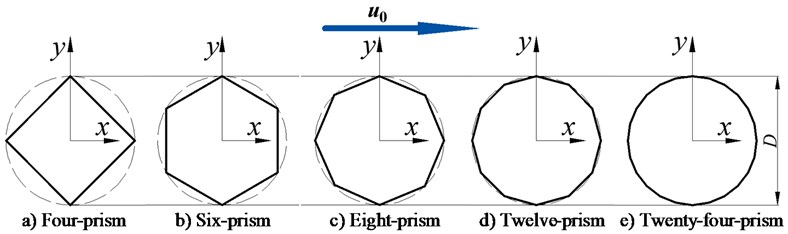
The direction of flow velocity $u_0$ and the position relations of the four-prism, six-prism, eight-prism, twelve-prism, twenty-four-prism and circular cylinder are shown in Figs. 1 and 2. In order to make the feature length of each projectile equal, the position of the projectile in the flow field is shown in Fig. 2. So that it is convenient to analyze the variation of the lift coefficient and drag coefficient of the projectile with different cross-section shapes.

According to the underwater trajectory of the projectile, the simulation test schemes are shown in Table 1. By changing the flow velocity and the shape of the cross-section, this paper studies the characteristics of the underwater flow field and the change rules of the lift and drag coefficient and the Strouhal number.

2.2. Grid division and turbulence model

The Kármán vortex is caused by the complex turbulent flows around the boundary layer of the cylinder, so the result of numerical simulation is directly affected by the quality of mesh. As shown in Fig. 3, the four-prism calculation flow field is divided into seven regions, and the flow field of six-prism, eight-prism and cylinder are divided into nine regions. In order to reduce the number of grids and accelerate the calculation speed, the grid density from the center of the area 4 or area 5 to the surrounding gradually reduces. As shown in Fig. 3(b), the O-type topological structure, which increases the density of grids around the projectile, is used to accurately observe the boundary layer of the complex flow and vortex shedding patterns, and the scale factor is 0.26. According to mesh-independent test results and the grid scale in the Ref. [5], the thickness of the first layer mesh of is 0.00001 m in the near-wall region, and the grid expansion factor in the radial direction (geometrical series) is 1.07 to assure high resolution grid in the boundary layer.

Fig. 3Topology structure of flow field mesh for projectile with different cross-sections

a) Topology structure of flow field mesh for four-prism

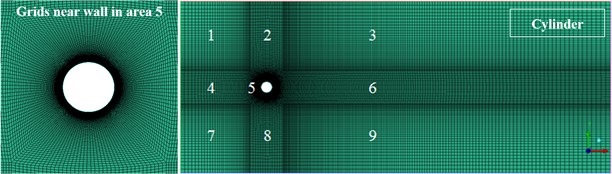
b) Topology structure of flow field mesh for circular cylinder

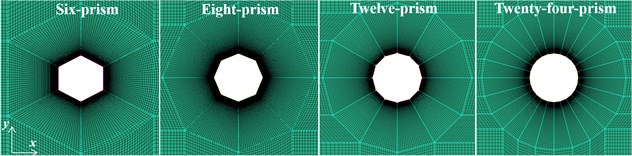
c) Grids near wall in area 5 for six-prism, eight-prism, twelve-prism and twenty-four-prism

In this paper, the Reynolds number (2.5×10⁵ $\le Re\le$2×10⁷) of circular cylinder flow is very high in the underwater ballistic. Usually, the Large Eddy Simulation (LES) model is used to simulate circular cylinder flow at high Reynolds number, but Large Eddy Simulation requires the computational grid is divided into the inertial temperament scale within the calculated time, and with the Reynolds number increasing, the number of grids increases in a geometric multiple [6]. And according to the research results of the Ref. [5], the two-dimensional RANS model is difficult to predict the unsteady flow around the cylinder. In 1997, Spalart [13] proposed DES. This method can not only play the small amount calculation of RANS in the boundary layer, but also can simulate the large scale separation turbulent flow in the region far away from the surface layer. So, in this paper, the S-A method of DES is used to simulate circular cylinder flow at the high Reynolds number.

According to the water medium compressibility, the velocity inlet boundary is used in entrance. The outflow is used in export. In order to reduce the influence of the wall on the velocity of the flow field, the upper and lower walls adopt the sliding wall, and the sliding velocity is consistent with the inlet velocity $u_0$. No slip surface is used in the surface of the columnar projectile. In the near wall, if the distinguishable LES mesh is used, a large number of grids are needed. Therefore, a method [24] similar to turbulent viscous model is adopted to deal with near wall mesh, and according to the reference, the near-wall scale $Y^{+}$ is maintained in 0.5-16, as shown in Fig. 4. The SIMPLEC algorithm is adopted to solve the pressure velocity coupling, the momentum is second order upwind scheme, the pressure equation is second order accuracy, and the second order implicit scheme is adopted in the transient scheme. The fluid medium is water medium, the density $\rho =$998.2 kg/m³, the dynamic viscosity $\nu =$1.003×10^-3 kg/(m·s). The Reynolds number $Re=\rho uD/\nu$.

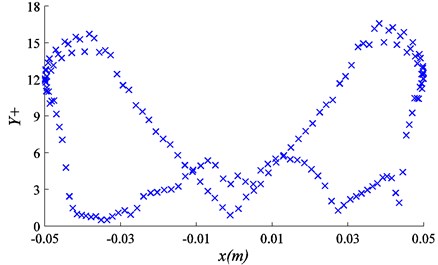
Fig. 4Y+ value on circular cylinder surface

2.3. Numerical verification

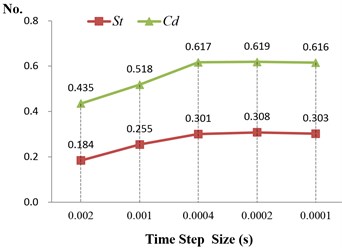
Studying the numerical calculation of circular cylinder flow, the calculation time step size $\mathrm{\Delta }t$ and mesh accuracy have direct influence on the simulation results. It is necessary to carry out the sensitivity tests of time step size and grids number, that is, a lot of simulation tests need to be done until the main parameters of the simulation results are not changed with the time step size and grids number. According to the experimental results in the Ref. [1], Kármán vortex can be established at $Re=$5×10⁶, and the main hydrodynamic parameters have smaller change rate near $Re=$5×10⁶, which is suitable for the sensitivity tests in this case. So, the flow velocity $u_0$ of circular cylinder flow is 50 m/s in the sensitivity tests of time step size and grids number. In each calculate time step size, the flow distance of the fluid is limited from $D$ to $D$/20. In numerical calculation of the sensitivity tests, the selected time step size is 0.002, 0.001, 0.0004, 0.0002 and 0.0001.

The numerical simulation results of sensitivity tests for time step sizes are shown in Fig. 5(a). The average drag coefficient $C_d$ and Strouhal number are defined as $C_d$ and $St$ respectively. The $St$ number and average drag coefficient $C_d$ increases with the decrease of time step size. When the time step size is less than or equal to 0.0004, the $St$ number and the average drag coefficient $C_d$ will not change with the change of time step size. When the time step size is 0.0004, the average drag coefficient $C_d$ is closest to the experimental value in the Ref. [1] than the others time step sizes. At the calculation time step size 0.0004, the flowing distance of the fluid is the 1/5$D$, where $D$ is the characteristic length. Combining the selection criterion of time step in the Ref. [14, 15], the calculation time step size satisfies a condition: $\mathrm{\Delta }t\times u_0\le D/5$ in the following simulation.

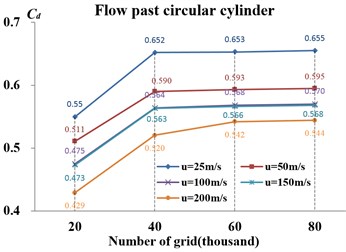
The sensitivity tests of grids number for flow past circular cylinder at 25 m/s-200 m/s are shown in Fig. 5(b). The total grid count from 20 thousand to 80 thousand is used to verify the independence of grids number. The results show that the convergence is presented, when the mesh number is more than 60 thousand in the working condition which $u_0=$200 m/s, $Re=$1.99×10⁷. The other working conditions can meet the requirement of precision when the number of grids is greater than 40 thousand. And, the total number of grids in each working condition is situated between 60 thousand and 66 thousand in the following simulation.

Fig. 5Sensitivity test of time step size and number of grid for St and Cd

a)

b)

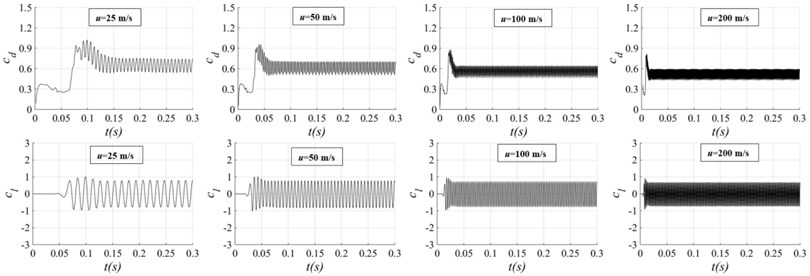
Fig. 6, respectively, is the time histories of the drag coefficient $c_d$ and the lift coefficient $c_l$ for circular cylinder flow with different flow velocity. In the scheme H1, the $c_d$ and $c_l$ are both periodic fluctuation after flowing 0.15 s, and the fluctuation frequency of $c_d$ is two times of the $c_l$. And the fluctuation frequency of $c_l$ is correspond to the vortex shedding frequency. The periodicity of the $c_l$ is better than the $c_d$, so the FFT algorithm is used to carry out the discrete Fourier transform of the lift coefficient curve, which can be used to determine the $St$ number related to vortex shedding. Because the amplitude fluctuation of the drag coefficient $c_d$ is larger in time-histories, the average drag coefficient $c_d$ is calculated after 0.15 seconds. In other working conditions, the drag coefficient $c_d$ and the lift coefficient $c_l$ have similar fluctuation characteristics, and the fluctuation frequency increases with the increase of flow velocity.

Fig. 6Time histories of the drag coefficient and lift coefficient with different flow velocity

In Fig. 7, the 2D DES results are compared with published 3D DES results [16] and experimental data [2] about $C_p$ in the turbulent separation flow ($Re=$3.0×10⁶ and $Re=$3.6×10⁶). At $Re=$3.0×10⁶, The separation point of 2D DES is very close to the 3D DES results, but the curvature of the $C_p$ is bigger than the 3D DES. At $Re=$3.6×10⁶, The separation of 2D DES occurs a little later than the experimental data. The crest of the 2D DES is smaller than the experimental data and 3D DES. The base pressure of the 2D DES fall between the experimental data and the 3D DES. These differences between the present work and the published data are in agreement with the two-dimensional LES simulation results [9], which are mainly caused by the difference in the fluid medium. The ability to sustain three-dimensionality in a 2D geometry is also confirmed by Travin A. [16] and Ong M. C. [17] at $Re=$1×10⁶, $Re=$2×10⁶, $Re=$3×10⁶, $Re=$3.6×10⁶. So, that hybrid methods (2D DES) can be used to the predict turbulent separation flow in underwater engineering.

Fig. 7Comparison with published 3D simulation and experimental data for the Cp

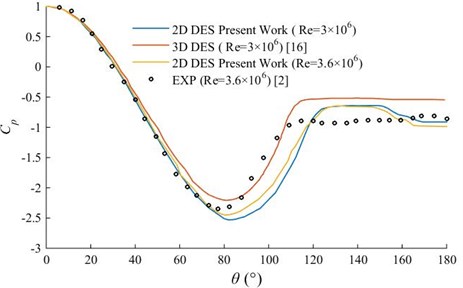
Table 2 is a comparison of present simulation results with published experimental and numerical data. When the flow velocity is 25 m/s, the average drag coefficient obtained in this paper and the Ref. [10] is larger than the experimental data [1]. The Strouhal number obtained in this paper is close to the Ref. [10], but is not in conformity with the experimental results in the Ref. [1]. When the flow velocity is 50 m/s and 100 m/s, the average drag coefficient and Strouhal number are both slightly larger than the experimental value in the Ref. [1], and are closer to the experimental values than the simulation results in the Ref. [10]. When the flow velocity is 150 m/s and 200 m/s and the Reynolds number $Re>$1.0×10⁷, the relevant experimental and simulation data are not found. According to the research of the Ref. [9], when the fluid medium is water, there is a negative pressure suction effect, so the resistance coefficient is greater than the experimental value. Thus, this is consistent with the simulation results in this paper.

3.1. The analysis of flow field characteristic

The vorticity map of circular cylinder flow with different flow velocity is shown in Fig. 8. The unit of coordinates is m. From the figure, it can be seen that when the flow velocity is in 25 m/s-200 m/s, the regular vortex forms in downstream tail flow region. With the flow velocity increasing, the propagation distance of the regular vortex increases, and the scale of the vortex in the y-axis direction increases first and then decreases. Because the size of vortex increases and the distance along the flow direction becomes smaller, the interaction between adjacent vortices increases, resulting in the shape of vortices gradually changing from a regular circle to a “P” vortex. When the vortex flows a certain distance, the ratio between the distances of transverse and flow direction is no longer satisfied by $h/l=$0.28 [1], and the vortex is no longer in regular and stable order.

The vorticity map of circular prism flow with different section shapes is shown in Fig. 9. From the figure, all flow around columnar projectile can form a relatively regular vortex street. The equilibrium distances of the vortices vary from one another. In the same distance of flow direction, the number of vortices arranged in equilibrium is positively related to the number of section edges, and coincides with the variation law of $St$ Number. For four-prism, the size of vortex street is the largest in the $y$-axis. The vortex shape of 24-prism is closest to the vortex of circular cylinder. And with the number of edges increasing, the size of the vortex street decrease. The scale of six-prism vortex in the $y$-axis direction is smaller than the four-prism, and the propagation distance of the regular vortex in the $x$-axis direction is less than the eight-prism. For 4-prism, 6-prism, the shape of vortices is circle, but for 8-prism, 12-prism and 24-prism, the shape of vortices is changed to a “P” vortex.

Fig. 8The Z vorticity of cylinder with different u0

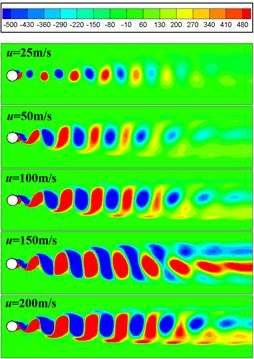
Fig. 9The Z vorticity of different column projectile

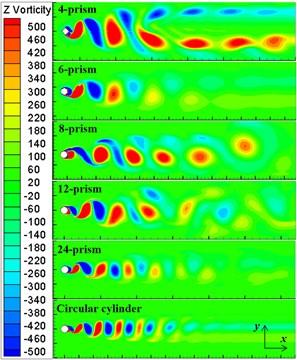
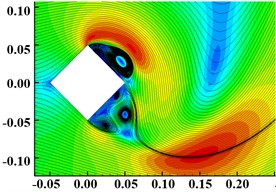
Fig. 10The Velocity and Streamline of prism with different section shapes

a) Four-prism

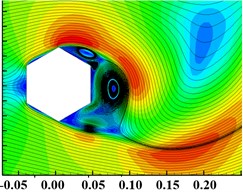
b) Six-prism

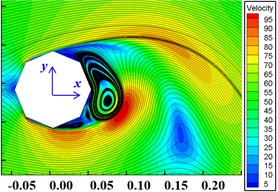
c) Eight-prism

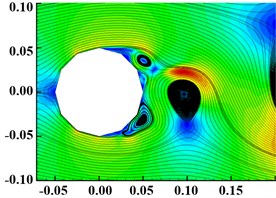
d) Twelve-prism

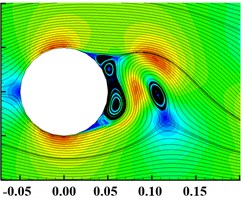
e) Twenty-four-prism

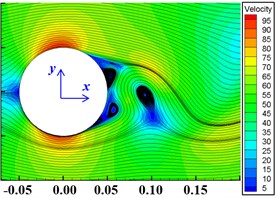
f) Circular cylinder

As shown in Fig. 10, the interior angle of quadrilateral is smallest, and the recirculation zone is the largest after the vortex separation point. When the fluid passes through the four-prism, the greater lateral velocity is obtained, so that the separation of positive and negative vortices is fastest, and the vortex scale is the largest, leading to the increase of pressure difference resistance. With the increase of the number of section edges and the interior angle, the recirculation zone and the size of vortex decrease. And, the vortex size of the twenty-four-prism is almost equal to the circular cylinder.

The distribution of the mean steady-state pressure coefficient $C_p$ along the column surface is shown in Fig. 11. The $C_p=2\left(P-P_0\right)/\rho u^2$, where $P$ is the monitoring pressure, and $P_0$ is the reference pressure. The reference pressure is zero in this paper. The statistical value of $C_p$ is the average of the pressure coefficient. It is shown from the diagram that the steady pressure coefficient shows good symmetry in the upper and lower surfaces of the cylindrical projectile. With the decrease of the number of section edges, the symmetry of $C_p$ circumferential distribution becomes worse. The stagnation point $C_p$ at the inflow is 1, and the pressure system decreases as the flow rate is resumed. The $C_p$ of 4-prism, 6-prism, 8-prism, 12-prism and 24-prism has multiple local minimum values at the polygon vertices of the cross section. The global minimum values of $C_p$ for 4-prism, 6-prism 8-prism, 12-prism and 24-prism are located at ${\theta }_4=$181.9°, ${\theta }_6=$150.0°, ${\theta }_8=$47.0°, ${\theta }_{12}=$60.0° and ${\theta }_{24}=$75.0°. The global minimum values of $C_p$ for cylindrical are at ${\theta }_{C1}=$83.5° and ${\theta }_{C2}=$275.4°. Subsequently, the pressure rises, and a relatively uniform low pressure zone is formed at the back of the projectile. And the less the number of edges of the column cross section, the smaller the pressure value in the low pressure zone.

Fig. 11Cp distribution on column surface

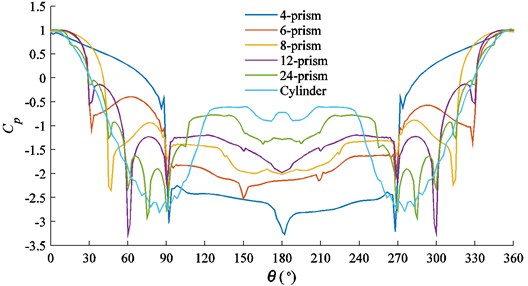
Fig. 12Mean velocity ux distribution along the axis y= 0

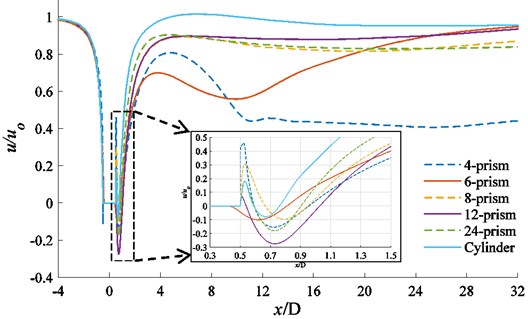
The mean velocity $u_x$ distribution along the central axis $y=$0 is shown in Fig. 12. When the fluid passes through the projectile body, the reflux velocity reaches the global maximum at $l_4/D=$0.218; $l_6/D=$0.191; $l_8/D=$0.292; $l_{12}/D=$0.225; $l_{24}/D=$0.221 and $l_C/D=$0.170 from the back of each columnar projectile. The global maximum reflux velocity of each prism is $u_4/u_0=$–0.155; $u_6/u_0=$ –0.100; $u_8/u_0=$ –0.095; $u_{12}/u_0=$–0.274; $u_{24}/u_0=$–0.179; $u_C/u_0=$ –0.077, and then the velocity distribution is gradually recovered. The length of reflux area for each prism is $L_4/D=$0.35; $L_6/D=$ 0.36; $L_8/D=$ 0.27; $L_{12}/D=$ 0.48; $L_{24}/D=$ 0.31; $L_C/D=$0.16.

The distributions of mean velocity $u_x$ at different positions behind each column are shown in Fig. 13. According to the diagram, in the near wake region of the column, the velocity range is ‘V’ in the $x$-axis direction. At $x/d=$0, with the number of edges increasing, the amplitude of the ‘V’ type of each prism increases. At $x/d=$1, with the number of edges increasing, the amplitude of the ‘V’ type of each prism increases first and then decreases. And at the others position, with the number of edges increasing, the amplitude of the ‘V’ type of each prism decreases. As the fluid moves away from the near wake region, the bottom of the ‘V’ type gradually slows down. The distribution curves of $u_x$ for eight-prism, twelve-prism, twenty-four-prism and cylinder have good symmetry about $y/D=$0. For the four-prism, the symmetry axis of the $u_x$ distribution curve shifts toward the positive direction of the $y$-axis at $y/D=$4, and the distribution curves of $u_x$ have good symmetry about $y/D=$0 at other locations. The symmetrical axis of the $u_x$ distribution curves at each position of the six-prism are shifted to the negative direction of the $y$-axis in different degrees.

Fig. 13The distributions of mean velocity ux at different positions behind each column

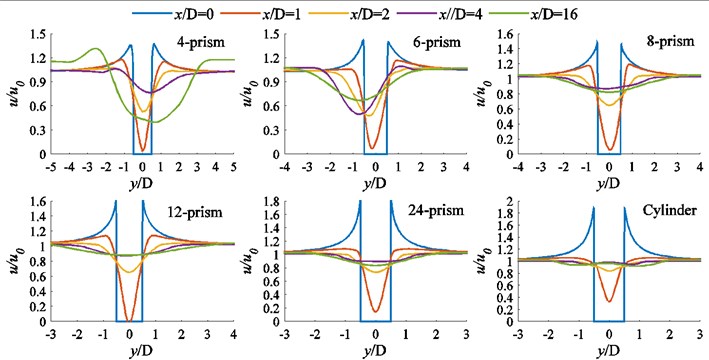
Fig. 14The distributions of mean velocity uy at different positions behind each prism

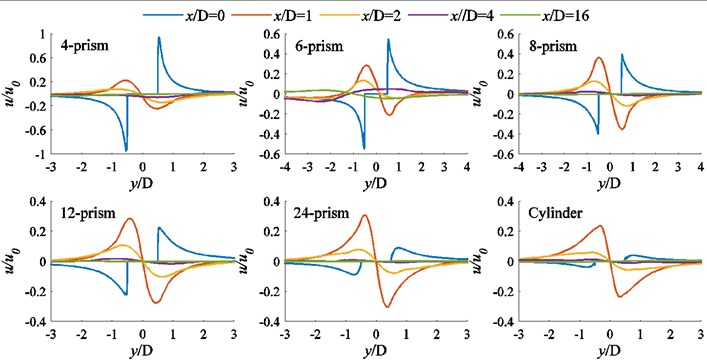
The distributions of mean velocity $u_y$ at different positions behind each prism are shown in Fig. 14. After flowing through the projectile, the fluid obtains a large lateral velocity at the $x/D=$0, $x/D=$1 and $x/D=$2 positions, and after $x/D\ge$4 the lateral velocity is almost attenuated to zero. In the $x/D=$0 position, comparing the six subplots, we can see that the lateral velocity decreases with the increase of the cross section edge number of the column. At the $x/D=$1 and $x/D=$2 positions, with the number of cross-section edges increasing, the lateral velocity of the fluid flowing through each prism increases first and then decreases.

3.2. The analysis of drag coefficient, lift coefficient and $\mathit{S}\mathit{t}$ number

Fig. 15 is the time histories of the drag coefficient $c_d$ and the lift coefficient $c_l$ for circular prism flow with different section shape. The flow velocity is 50 m/s. The flow is fully developed. After the full development of the flow field, spectrum analysis of the time histories shows that the lift coefficient and drag coefficient of the four-prism, twenty-four-prism and cylinder tend to be single periodic vibration. And the drag coefficient and lift coefficient of the six-prism tend to be multi-periodic and high amplitude vibration, that is, there is a high order harmonic component in addition to the main frequency. The drag coefficient and lift coefficient of the eight-prism and twelve-prism is poor in single periodicity.

Fig. 15Time histories of the drag coefficient and lift coefficient for different prisms

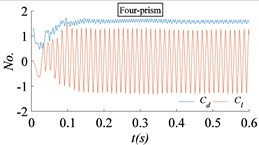
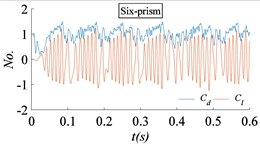
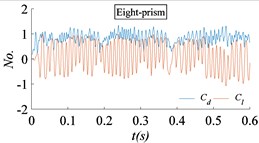
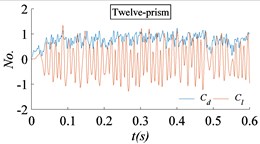
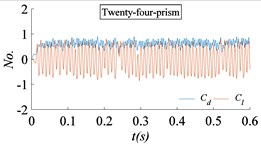
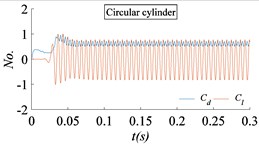
Fig. 16The power spectral density (PSD) of lift coefficient for different prisms

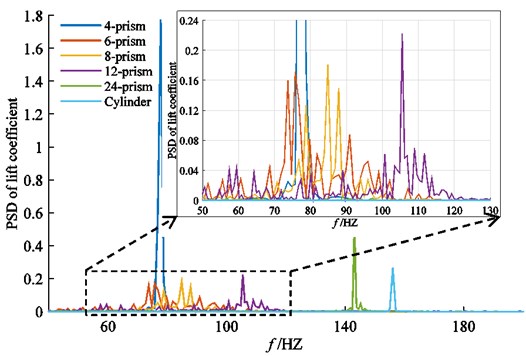
As shown in Fig. 15, the fluctuating hydrodynamics time histories of six-prism, eight-prism and twelve-prism are irregular and exhibit stochastic fluctuation characteristics. Therefore, statistical methods are needed to obtain hydrodynamics parameters such as mean value and fluctuating RMS, so power spectrum analysis is needed to obtain the frequency domain characteristics. In order to eliminate the influence of initial calculation on the calculation results, the first 1/6 part of hydrodynamics lift and drag time history is eliminated, that is, it is not involved in hydrodynamics statistical analysis and frequency domain analysis. The power spectral density analysis of the lift coefficient time history is shown in Fig. 16.

In this paper, the $f_{max}$ of global maximum peak is defined as the frequency of main vortex shedding and the corresponding $St$ is defined as the $St$ Number of main vortex shedding. As shown in Fig. 16, with the number of edges increasing, the frequency of vortex shedding is also gradually close to the circular cylinder. And the power spectra density of lift coefficients time histories for four-prism twenty-four-prism and cylinder are single peaks, respectively $f_{4max}=$77.78 Hz, $f_{24max}=$143.1 Hz $f_{Cmax}=$ 156.67 Hz. There are many obvious peaks in the power spectra density of lift coefficients time histories for six-prism, eight-prism and twelve-prism. They are $f_{61}=$73.74 Hz, $f_{62}=$90.91 Hz, $f_{6max}=$75.76 Hz; $f_{81}=$78.79 Hz, $f_{8max}=$84.85 Hz, $f_{82}=$ 87.88 Hz; $f_{121}=$ 108.9 Hz, $f_{12max}=$105.5 Hz. It can be seen that there are many frequencies of the vortex shedding for six-prism, eight-prism and twelve-prism projectile, that is, the energy of vortex shedding is not gathered at one frequency but concentrated in a frequency band. The vortex shedding frequency of six-prism and eight-prism is multiple and more dispersed than four-prism, twenty-four-prism and cylinder. Therefore, it is difficult to cause the flow induced structural vibrations for six-prism and eight-prism. Although there are multiple vortex shedding frequencies for twelve-prism, they are too concentrated. In the power spectral density of six-prism, eight-prism and twelve-prism, there are also many small peaks, which are obviously lower than those frequencies and probably also the frequency of vortex shedding. In addition, the average lift of each prism is very small, so the average lift can be treated as zero.

The average drag coefficient $C_d$ and the Strouhal number of the cylindrical projectile with different flow velocity are shown in Fig. 17. The average drag coefficient $C_d$ decreases with the increase of the Reynolds number, and the Strouhal number increases with the increase of the Reynolds number. This is consistent with the experimental results in the Ref. [1]. After $Re>$9.96×10⁶, the average drag coefficient $C_d$ decreases slowly, and the Strouhal number increases slowly. Under the premise of satisfying the shrapnel power radius, scheme H2 should be selected first in engineering design.

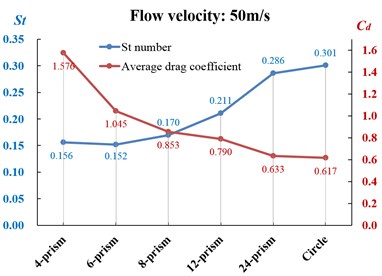
The average drag coefficient $C_d$ and the Strouhal number of the prism projectile with different cross-sections are shown in Fig. 18. With the edges number of cross-section increasing, the average drag coefficient $C_d$ decreases, and the Strouhal number increases. Combined with the vibration frequency spectrum analysis of the lift and drag coefficient in Figs. 14-15, and considering the factors such as drag reduction, the power of shrapnel and avoiding resonance, the projectile with octagon cross-section is more suitable for engineering applications.

Fig. 17Cylinder’s Cd and St with different Re

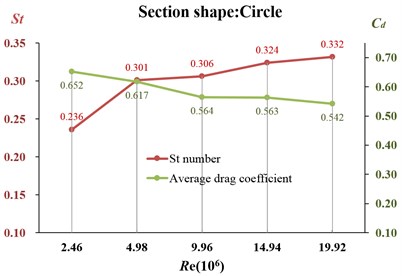
Fig. 18Cd and St with different section shape