Abstract
It was determined that a preliminary assessment of the complexity in the design stage of pre-production can help to determine the feasibility of entering new products into production, and its future costs. It is shown that the advantages of fuzzy expert systems are: the ability to parallel execution of existing rules; the multiplicity of interpretations of variables, providing superposition of states and the possibility of conflicting rules; prediction of new state of the system; description of the problem and the rules of natural language using the linguistic variables.
1. Introduction
Almost any enterprise engaged in the production of engineering products in the current market conditions is faced with the need for a rough estimate of the complexity of the product without the design process [1]. This is especially true for small-scale and individual productions. Preliminary assessment of the complexity in the design stage of pre-production can help to determine the feasibility of entering new products into production, and its future costs [2].
2. A method for constructing fuzzy decision trees
Each decision tree generates a certain set of rules. If you use the algorithm of decision trees to generate fuzzy rules, you can go to the fuzzy inference system.
The algorithm of fuzzy inference on the basis of a decision tree.
We consider the decision tree constructed as a set of fuzzy rules of the form if then is , .
Conditions corresponds of the condition to the separation the set of objects , ; means entering the value in the fuzzy interval with membership functions:
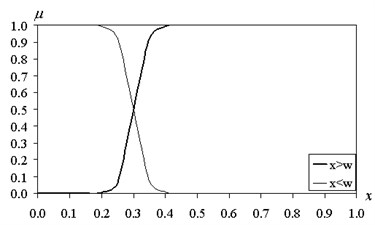
Function of accessory corresponds to a condition of , and to a condition of .
The graphs of membership functions are shown in Fig. 1 and Fig. 2.
The value characterizes the blur interval. When fuzzy interval returns to normal.
For a given vector are determined by the degree of truth for each rule: , . Degrees of truth correspond to the values of membership functions of the left sides (prerequisites):
where – the number of terms in this rule .
Fig. 1The functions of fuzzy intervals (β= 10)
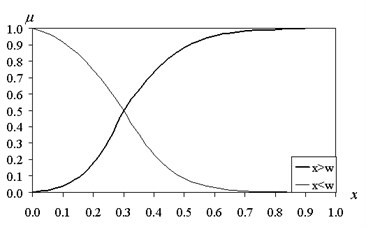
Fig. 2The functions of fuzzy intervals (β= 50)
As a result, the aggregate output signal is determined by the formula:
Coefficients ; are determined by the available training set using pseudoinversion procedure. , training samples are used for training. Under fixed rates is written , in the form of a system of linear algebraic equations:
or . If the number of equations is greater than the number of unknowns , the matrix has a rectangular shape. In this case, use pseudoinversion operation. To this end, the transposed matrix is multiplied by the left and right side of the equation . The resulting matrix equation is solved with respect to the unknown vector : , where .
The output value of the network are as follows: , .
Thus, we obtain the following algorithm for constructing a fuzzy decision tree. On a set of training data is constructed a decision tree with the classes of discrete values of the output variable. Formed rules. Sets the type of membership functions for the conditions. Calculates the degree of truth for each rule. Is determined by a set of training data weights ; . It calculates the continuous value of output variable in accordance with the fuzzy inference of Sugeno. Along with the Sugeno [6] fuzzy inference can be made on the conclusion by Mamdani [7]. In this case, stored steps 1-4 algorithm. Specifies membership function for the right side of the rules. Number of membership functions is equal to the number of classes , which divided the output variable. We have dealt with triangular membership functions. Implemented maximum composition or combination of features obtained: . By using centroid method of defuzzification is carried out and the evaluation is [3].
3. The results of the numerical experiment testing the method of fuzzy decision trees
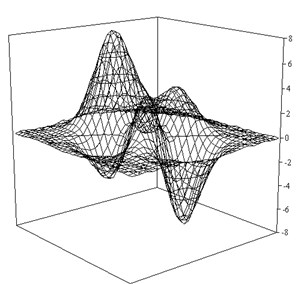
The above algorithms were tested on a test considered the function . In Fig. 3 shows the reconstructed surface of the function .
The entire sample is divided into two equal parts. Constructing a tree corresponds to 57 units, 29 of the rules, 10. The mean square error on the test sample was 2.66 %.
An even better result is achieved by increasing the number of classes to 10. The mean square error on the test sample is 0.78 % and 0.25 % of the training. This tree contains 93 rules for 5.
Fig. 3Recovery of function ψ as a result of fuzzy inference on Sugeno (K= 5)
In the tree structure and, consequently, the accuracy of the forecast is influenced by various factors [5]: the setting of membership functions ; the minimum number of elements in the set are separated by ; the ratio of the volume of training and test samples.
Fig. 4 shows the value of the mean square error recovery on the value of to 3, 3. On Fig. 4 thin lines correspond to the fuzzy inference by Sugeno (solid – test sample, open circles – training). The increase in reduces the errors in the derivation by Mamdani. There is an optimal value of the parameter 10, and is laid in the subsequent calculations for Sugeno fuzzy inference. To output on Mamdani value assumed 50. Fig. 4 also implies that the magnitude of the approximation error test function for fuzzy inference by Mamdani significantly higher (10.8 % for 50 for sample screening) than to output on Sugeno (1.9 % at 10 as the test sample).
On the complexity of the tree affects the minimum size of the shared sets . In Fig. 5 shows the number of rules that characterize the tree, the size of .
From Fig. 5 it follows that an increase in the size of leads to a simplification of the tree structure and to reduce the number of rules for any number of classes from 3 to 10. Increasing the number of classes also complicates the tree and increases the number of rules.
Since the increase in the size of the set of shared affect the structure of the tree, it was studied numerically, depending on the value of the prediction error . The results are shown in Fig. 6, 7.
With increasing numbers of error on the training sample has a tendency to increase due to the formation of mixed grades.
On the test sample with an increase in the number of classes we observed the appearance of a certain optimum value . This results in the test sample is an indicator of the quality of learning and generalizing patterns.
Fig. 4The dependence of an error recovery on parameter fuzziness interval
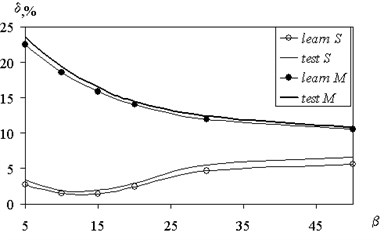
Fig. 5The dependence of number of rules on the minimum size of the divided set
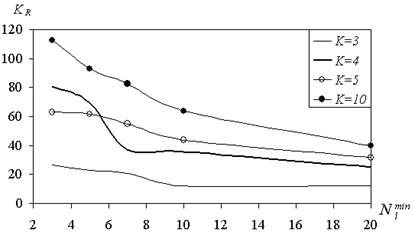
Fig. 6The dependence of the reconstruction error of the minimum separating set (training sample)
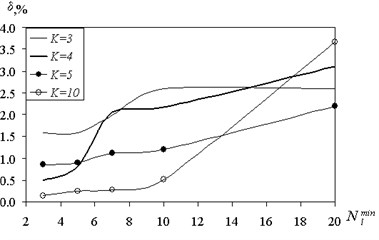
Fig. 7The dependence of the reconstruction error of the minimum separating set (the test sample)
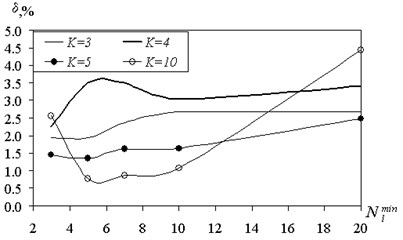
For small of the tree structure is too complex, and the ability to generalize reduced. On the training sample did not occur because there is data storage. Here, the same effect as in retraining the neural network. If the allowable size of the shared the set of substantially increased, the formation of mixed classes starts increasing forecast accuracy.
The presented results are obtained when the ratio of training and test samples 50-50. Fig. 8 shows the effect of partitioning the training set of predictive accuracy.
forecasting error was determined on the test sample. Plearn = 0.8 means that the amount of training samples is 80 % of the total amount of data, and on the test sample accounts for 20 %. Meaning Plearn = 0.25 corresponds to the situation: 25 % – training sample, 75 % – screening. Reducing the amount of data available for training, increases the error. Particularly strong increases uncertainty for large values of . According to Fig. 8 corresponds to the number of classes 5.
A suitable value prediction error of 3.25 % was obtained by reducing the volume of training sample to 10 %. Reducing the amount of training data for up to 5 % results in poor prediction quality. However, a discrete classification gives 69 % of correct partition classes. In case of the continuous output variable computation of coefficients of ; on the available training selection using the procedure of pseudo-inverse is required. For a small amount of sample matrix approaching to the square, and the ability to generalize the fuzzy tree is sharply reduced. Changing the number of rules and forecasting errors with the increasing volume of training data is shown in Fig. 9.
Number of rules is increased, improving the coverage of the rules of all the examples from the training set and the prediction error is reduced.
Compare calculated by the proposed method of fuzzy trees and the actual values of the test functions for training and screening of samples is shown in Fig. 10.
The correlation coefficient for the training sample was 0.9992 and 0.9963 for the test. The corresponding values of the mean square error was 0.53 % and 1.21 %.
Fuzzy conclusion on Mamdani does not receive the benefits in comparison with the conclusion by Sugeno in all cases except one. As noted above, for a small number of snapshots determining weighting factors using pseudoinversion operation leads to a large prediction error. Fuzzy conclusion on Mamdani by giving a more realistic value of the output variable.
Fig. 8The dependence of the reconstruction error of the minimum shared set under a different ratio of the volume of training and test samples
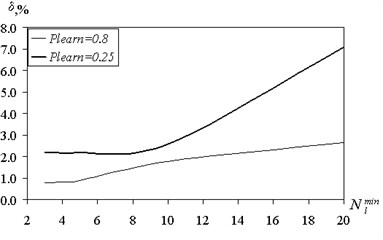
Fig. 9Influence of the volume ratio of the training and test samples to recover the error and the number of rules
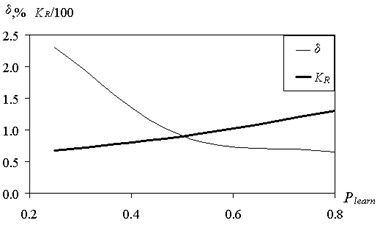
Fig. 10Comparison of the calculated method of fuzzy trees and the actual values of the test function: a) training sample, b) screening sample
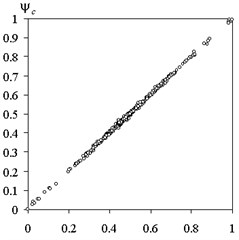
a)
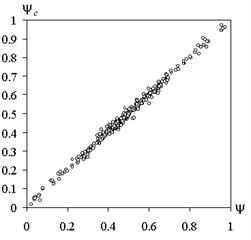
b)
An algorithm for constructing a fuzzy decision tree is characterized by a small number of settings. Actually these three parameters: index of fuzziness interval , the size of shared set and the number of classes into which the continuous values of the output variable . If the output is a discrete variable, then the value is uniquely determined. For a continuous function select value enough of the [2, 5] range. The value 10 is optimal for output by Sugeno, and 50 for fuzzy inference according to Mamdani. Setting the size of shared the set is dependent on the type of the analyzed data. If the data are characterized by high noise and the sample size is large enough, then the value 20-50. If the data is consistent 3-5. Education fuzzy tree actually does not require iterations. Construction of the tree allows a single step to determine the weights and train the system. Building a tree with the number of nodes of 500 does not take more than a 1 second on a standard PC, the definition of the weighting factors to the number of rules 120-150 requires 3-5 seconds. These computational cost significantly lower than required in the training of neural networks. The algorithm is suitable to solve both problems of classification, and approximation.
4. The addition of expert rules
If necessary, the possible involvement of experienced experts to add rules that determine some of the properties the product in question and the impact on the amount of labor input [4]. These rules have the general form: if then is , .
Now, the condition is the value of to hit one of the intervals into which the range of the broken down of . In this way, , , where – left and right boundaries of the intervals (tones). At each interval set membership function: , ; ; .
Membership functions can be set triangular, trapezoidal or in the form of a Gaussian function.
Aggregate output signal is given by Sugeno:
After adding the new rules coefficients recalculated with the calculation of a new matrix .
5. Conclusions
The advantages of fuzzy expert systems are: the ability to parallel execution of existing rules; the multiplicity of interpretations of variables, providing superposition of states and the possibility of conflicting rules; prediction of new state of the system; description of the problem and the rules of natural language using the linguistic variables.
Thus, the process of construction of adaptive fuzzy system is always reduced to the solution of a finite set of optimization problems. View optimization function depends entirely on data from the training set. Finding global extremum of this function by traditional methods of optimization is a difficult, and often impossible task. Therefore, new hybrid algorithms should be used for training the fuzzy system.
Information systems, applying the methods of fuzzy logic, provide a more stable and complete understanding of existing knowledge about a certain subject, as compared to traditional expert systems. Therefore, they are widely used in tasks of decision making under uncertainty.
References
-
Lyalin V. E. Mathematical Models and Intellectual Information Technologies for Increase in Efficiency of Production Organization. Monograph, KNTs RAS Publishing House, Murmansk-Izhevsk, 2006, p. 296.
-
Silkin A. Yu., Volovnik A. D., Lyalin V. E. Indistinct clusterization contractors at acceptance of decisions of price discrimination on the basis of formal criteria. Journal Audit and Financial Analysis, Vol. 2, 2006, p. 47-93.
-
Lyalin V. E., Serazetdinova T. I. Mathematical Modeling and Information Technologies in Economy of the Entity. Monograph, KNTs RAS Publishing House, Murmansk-Izhevsk, 2005, p. 212.
-
Vasiliev V. A., Lyalin V. E., Letchikov A. V. Mathematical models of an estimation and management of financial risks of managing subjects. Journal Audit and Financial Analysis, Vol. 3, 2006, p. 103-160.
-
Suchkova E. A., Lyalin V. E. Problems of the choice of the supplier – criteria, tools and evaluation methods. Mathematical Models and Information Technologies in Production Organization, Vol. 2, 2012, p. 39.
-
Lyalin V. E., Volovnik A. D. Mathematical modelling of investment risk by optimization of operation of business. Journal Audit and Financial Analysis, Vol. 2, 2006, p. 10-46.
-
Lebedeva T. I., Lyalin V. E. Economic-mathematical modeling of development of the region. The Deposited Manuscript No. 346-B2005 3/15/2005, 2005.
