Abstract
Embedded fault diagnosis machine for the automatic ammunition loading system real-time monitors the automatic ammunition loading system, collects the data by using sensors, analyzes the data, detects and isolates faults, or predicts the health of the system in the future. The denoising of the collected data is of great significance to effectively reveal the operation information of ammunition automatic loading system. In order to solve the problem of the traditional median filter could not be taken into account the details and the smoothness, a filtering method based on wavelet transform for automatic ammunition loading system is proposed in this paper. This method can effectively reduce the noise and improve the signal noise ratio (SNR), the signal after wavelet filter retains all the low frequency of the single axis swing, filters out the high frequency noise. It ensures the correctness of the follow-up data analysis and processing, detection, isolation of the fault or predict the health of the system.
1. Introduction
Embedded fault diagnosis machine for the automatic ammunition loading system real-time monitors the automatic ammunition loading system, collects the data by using sensors, analyzes the data, detects and isolates faults, or predicts the health of the system in the future. Fault diagnosis mainly includes signal detection, feature extraction, state diagnosis and state analysis and so on [1, 2]. The denoising of the collected data is of great significance to effectively reveal the operation information of ammunition automatic loading system. In order to solve the problem of the traditional median filter could not be taken into account the details and the smoothness, a filtering method of collecting data based on the wavelet transform for the collected data of ammunition automatic loading system is put forward in this paper, it can reduce the noise signal and improve the signal noise ratio (SNR), and provides a new idea for the application of wavelet analysis in fault diagnosis and military field.
2. Theory of wavelet filtering
2.1. Definition and characteristics of continuous wavelet transform
The continuous wavelet transform of the signal is defined as Eq. (1):
In Eq. (1):
is wavelet basis function, a is scale factor, b is translation factor.
Choosing proper mother wavelet can make and its Fourier transform have better local property, so wavelet analysis is a time-frequency analysis [3].
2.2. Basic principle
A signal model with noise is as follow:
In Eq. (3), is original signal, is noise. The signals detected in the engineering are often mixed with noise, and signal denoising is one of the classical problems in the field of signal processing. The purpose of signal denoising is to suppress the noise in the signal , reproduction signal . The traditional denoising method will raise the entropy after signals transform, and the non-stationary characteristics and correlation of the signals could not be depicted [4].
Wavelet transform has the following properties: 1) Time-frequency localization characteristics; 2) Multi resolution characteristics; 3) Solution related properties; 4) Flexibility of mother wavelet selection. 1 and 2 determine that the wavelet filtering method can remove the noise while retaining the abrupt change information of the signal [5]. After wavelet transform, the wavelet coefficients are mainly composed of the details of the noise and the signal. Therefore, wavelet filtering is to use the prior knowledge of the specific problems, according to the mechanism of signal coefficient and noise coefficient with different properties at different scales, constructing the corresponding rules, processing the coefficients of signal with noise in the wavelet domain. The purpose is to reduce or eliminate the noise coefficient completely, at the same time, to maximize the retention of the signal coefficient, to obtain the optimal estimation of the real signal.
Wavelet filter is not to smooth signal, but try to remove all the noise, retains the real signal. Filtering is the processing of wavelet coefficients in the wavelet domain. The filtering process is generally completed by three steps: 1. wavelet transform; 2. nonlinear processing the wavelet coefficients in order to filter out the noise; 3. inverse wavelet transform [6].
3. Comparison of median filtering and wavelet filtering
Embedded fault diagnosis machine for the automatic ammunition loading system using the USB-6211 data acquisition card of the National Instruments Corporate made in United States to automatically collect the data of coordinate action angular velocity of the automatic ammunition loading system. The sampling frequency is 1 kHz, and a complete single axis swing lasts for two seconds, will get 2048 data, as shown in Fig. 1.
Fig. 1Data of the coordinate action angular velocity sampled
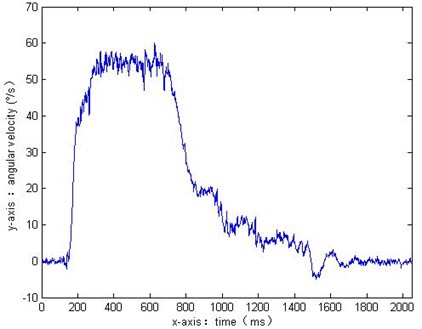
The data of coordinate action angular velocity is low frequency signal, the sampling signal contains high frequency noise. If the traditional median filter is used to smooth the signal, the value of each point is set to the value of all points in the n neighborhood. The filtering results are shown in Fig. 2 when 3.
Fig. 2The filtering results when n= 3
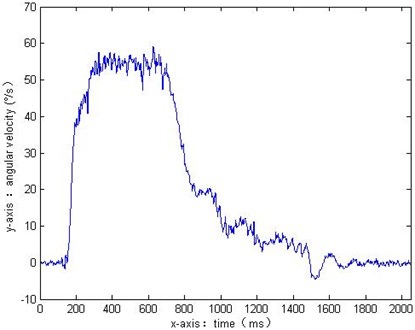
The filtering result is not ideal on smoothness, the high frequency noise is mostly reserved. If in order to smooth the signal, increase the value of , the filtering results are shown in Fig. 3 when 1024.
Fig. 3The filtering results when n= 1024
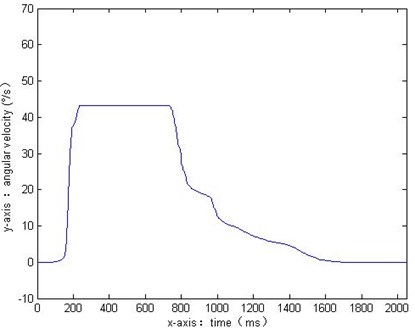
The details will be lost if excessive smoothing the signal, resulting the distortion of the signal after filtering. Therefore, the median filtering could not be taken into account the details and the smoothness, but wavelet filter can solve this problem very well. The data of coordinate action angular velocity is low frequency signal, all the high frequency part of the collected signal can be considered as noise. Therefore, the db4 wavelet is used to decompose the collected signal in 5 layers of multi scale decomposition, and keep the low frequency information only, high frequency coefficients are all set zeros. The decomposed low frequency signal is shown in Fig. 4.
It can be seen that the signal after the wavelet filter retains all the low frequency of the single axis swing of the ammunition auto loading system, filter out the high frequency noise. The signal is more smoothly than median filtering, and no distortion. Ensure the correctness of the follow-up data analysis and processing, detection, isolation of the fault or predict the health of the system.
Fig. 4The wavelet filtering results
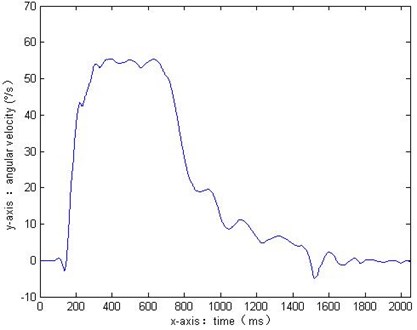
4. Conclusion
In order to solve the problem of the traditional median filter could not be taken into account the details and the smoothness, a filtering method based on wavelet transform for automatic ammunition loading system is proposed in this paper. This method can effectively reduce the noise and improve the SNR, ensure the correctness of the follow-up data analysis and processing, detection, isolation of the fault or predict the health of the system, made useful exploration for the application of wavelet analysis in fault diagnosis and military field.
References
-
Vachtsevanos George, Lewis Frank L., Roemer Michael, et al. Intelligent Fault Diagnosis and Prognosis for Engineering Systems. National Defense Industry Press, Beijing, 2013.
-
Cheng Fabin, Tang Baoping, Zhao Ling A filtering method based on optimal Morlet wavelet and its application in machine fault feature analysis. China Mechanical Engineering, Vol. 19, Issue 12, 2008, p. 1437-1441.
-
Rioul O., Vetterli M. Wavelets and signal processing. IEEE Signal Processing Magazine, Vol. 8, Issue 4, 1991, p. 14-88.
-
Wang Huiqin Wavelet Analysis and Application. Beijing University of Posts and Telecommunications Press, Beijing, 2011.
-
Vidakovic B. L., Ozoya C. B. On time-dependent wavelet denoising. IEEE Transactions on Signal Processing, Vol. 46, Issue 9, 1998, p. 2549-2551.
-
Pan Quan, Meng Jinli, Zhang Lei, et al. Wavelet filtering method and its application. Journal of Electronics and Information Technology, Vol. 29, Issue 1, 2007, p. 236-242.
