Abstract
Oversampling is used at traditional signal processing, but with the big data developing, oversampling has the disadvantages that do not meet the high-volume and high-velocity, so we apply the theory of compressed sensing to sample mechanical vibration signals with undersampling, and get the better observation matrix and reconstruction algorithm which are suitable for the vibration signal. The reconstruction error is quantified by the numerical simulation. The comparison results of the time and frequency domain before and after signal reconstruction are carried out. The simulation results show when the sampling frequency is one fifth of the traditional sampling frequency, the error of the characteristic parameters between the original signal and reconstruction signal is less than 7 % in the time domain, and the main frequency components of the reconstruction signal do not change in the frequency domain, which can meet the engineering applications.
1. Introduction
Under the background of big data, the wider signal bandwidth is, the bigger the data volume is, which put forward higher requirements for the signal processing ability and the hardware equipment. The traditional sampling method cannot satisfy the high demand of sampling rate, so the undersampling method based on compressed sensing has been widely used [1]. At present, the sparsity of one-dimensional vibration signal is poor and narrow bandwidth, so which would be less researched and applied, and the compressed sensing theory is mainly applied to two-dimensional image signal [2-4], which limits the big data acquisition in the field of mechanical applications. In this paper, we get the observation matrix and reconstruction algorithm that adapt to the vibration signal with the research on the observation matrix and reconstruction algorithm. Then, we have simulated the compressed sensing vibration signal and quantified the reconstruction error. The research is proved that the sampling method based on compressed sensing can realize the undersampling of the vibration signal. Through comparing the reconstruction errors in the time domain and difference f frequency components in the frequency domain between the reconstruction signal and original signal, it proves that the compressed sensing can be well applied to the mechanical vibration signal, which has a positive effect on the sampling, transmission and processing of the signal under big data background.
2. Compressed sensing theory
In 2004, Candes, Donoho, Romberg, Tao etc. [5] proposed a new sampling theory based on sparse signal, which is called compressed sensing (CS). It can realize the signal undersampling. CS theory turns signal sampling to information sampling, which is no longer to sample the entire signal with high-speed, but to sample parts which are carrying information at low-speed. The theory is different from the traditional Shanon/Nyquist sampling theorem, which can directly sample a few of linear observations. These observations are compressed signal, and contain all information of the original signal. Finally, the original signal can be reconstructed by an optimization algorithm.
The framework of CS theory includes three parts: sparse representation of the signal, the linear observation of the signal, and the precise reconstruction of the signal, as shown in Fig. 1.
Fig. 1Theory framework of compressed sensing

3. Sampling implementation of vibration signals based on compressed sensing
3.1. Determination of the observation matrix
The observation matrix is a mathematical tool to simulate the undersampling signal. The determination of the observation matrix is based on construction of the matrix, the numbers of observation, and the characteristics of the signal. Several common observation matrices are as follows: Gaussian random observation matrix, Bernoulli random observation matrix, Partial Hadamard observation matrix, Partial Orthogonal observation matrix, sparse random observation matrix. By studying the construction of several matrices and the numbers of observation, the Gaussian random matrix is determined as the observation matrix of the vibration signal. The reasons are as follows: Firstly, the vibration signal is a one-dimensional signal, and the simulation experiment has proved that the Gaussian random observation matrix shows a good performance in the observation process of the one-dimensional signal [6]. Secondly, Gaussian random observation matrix has been proved to meet the RIP nature [7, 8], and the experimental simulation has been proved Gaussian random observation matrix has a high reconstruction precision under OMP reconstruction algorithm. Finally, Gaussian random observation matrix is uncorrelated with most of the orthogonal Sparse basis, which is convenient for the selection of sparse basis in the reconstruction process. Compared with the Gaussian random observation matrix, the Bernoulli Stochastic observation matrix is worse on the uncorrelated with the sparse matrix; Partial Hadamard observation matrix is limited by the sampling value of , which limits its application; Partial Orthogonal observation matrix requires a higher numbers of observation; the probability of the sparse random observation matrix satisfying RIP is lower.
3.2. Determination of the reconstruction algorithm
An important part of compressed Sensing is to achieve the reconstruction of the observed signal by Using reconstruction algorithm the choice of reconstruction algorithm has a great influence on the reconstruction error.
Similar to the determination of the observation matrix, there are several common reconstruction algorithms: Matching Pursuit (MP) algorithm, Orthogonal Matching Pursuit (OMP) algorithm, Segmented Orthogonal Matching Pursuit (StOMP) algorithm. Through the research of the above algorithms, the Orthogonal Matching Pursuit algorithm is determined as vibration signal reconstruction algorithm. The reasons are as follows: compared with the MP algorithm, the efficiency of OMP algorithm is higher. Compared with the StOMP algorithm, the OMP algorithm does not need the threshold, which makes the implementation of the algorithm simpler, lower complexity the algorithm. The OMP algorithm is used in the simulation experiment of the vibration signal, which shows a good performance of reconstruction. With comparison and analysis of the above three greedy algorithms, at the same time, considering the matching degree with Gauss random observation matrix, so the OMP algorithm (OMP) is used to determine the signal reconstruction algorithm of the sampling system.
3.3. Sampling implementation and quantization error
This paper uses the stationary random test signal for simulation. The program flow chart for observing and reconstructing the vibration signal is shown in Fig. 2. Operating the procedure, the results of the signal reconstruction as shown in Fig. 3.
Fig. 2Program flow chart of system
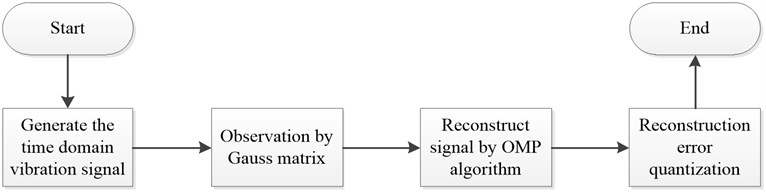
Fig. 3Comparison chart of recovery signal and original signal for stable signal
It can be seen from Fig. 3: the simulation system can reconstruct the original signal, which shows that the choice of the observation matrix and the reconstruction algorithm is correct. At the same time, it can be seen from the Fig. 3 that the reconstructed signal and the original signal are basically coincident, which shows that the system can achieve a relatively high accuracy for reconstruction.
3.4. Reconstruction error quantization
Norm-2 refers to the square root of sum of square of mode value of all elements. Namely, it refers to the distance for geometric meaning. According to the idea, construct norm-2 between the reconstructed signal and the original signal, namely, the cumulative distance between the corresponding points, so as to realize the quantization of the signal reconstruction error.
This process can be implemented by using the norm function of the MATLAB program. Run the program, the result is 1.71022.
Since the quantization error is achieved by norm-2, and norm-2 means distance, so, the closer zero the quantization error is, the smaller the reconstruction error is, and the higher the reconstruction precision is.
4. Signal contrast before and after reconstruction
4.1. Time domain comparisons
Fig. 3 is the contrast between traditional sampling and compression sensing sampling in the time domain. That is the contrast between the reconstructed signal and the original signal.
The time-domain characteristic parameters of the original signal and the reconstructed signal are compared as shown in Table 1.
It can be seen from Table 1 that the error of the time domain characteristic parameters between the original signal and the reconstructed signal is guaranteed within 7 %. The approximate accurate reconstruction of the sampled signal can be achieved.
Table 1Comparison of the time domain feature parameters between original signal and reconstruction signal
Item | Peak value / V | Mean value / V | Effective value / V |
Original signal | 1.300 | –0.0015 | 0.919 |
Reconstructed signal | 1.383 | –0.0014 | 0.978 |
Error percentage (%) | 6.385 | 6.667 | 6.420 |
4.2. Frequency domain comparison
The reconstructed signal is subjected to fast Fourier transform, which compared with the fast Fourier transform of the traditional sampling method as shown in Fig. 4 and Fig. 5.
Fig. 4Traditional sampled signal spectrum
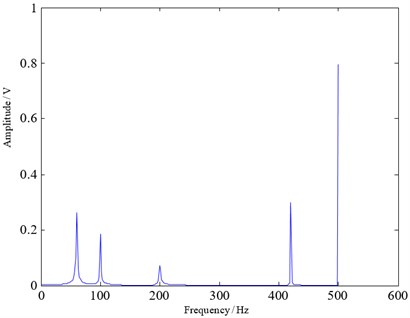
Fig. 5Reconstructed signal spectrum
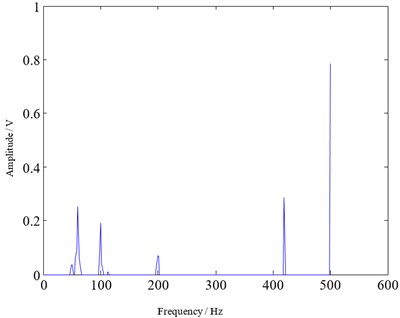
From Fig. 4 and Fig. 5, it can be seen that the frequency component and the amplitude of the reconstructed signal spectrum are basically the same as the traditional sampling signal spectrum. The difference is that, the reconstructed signal has some non-smooth and isolated narrow band in the spectrum. The reason is that the original signal is approximately sparse but not completely sparse, so there will be errors in the reconstruction process. These errors in the frequency domain on the performance are certain non-smooth and isolated narrow band. In fact, due to the need to recover a sparse signal during reconstruction, it concentrated the originally widely distributed energy on some frequency bands, causing some of the original bands been broken, many isolated points and narrow bands appear.
4.3. Comparison of traditional sampling and compressed sensing sampling
The ultimate goal of compressed sensing is to implement the undersampling, which reduces the sampling frequency. Traditional ways of classical sampling have clear a request for the sampling frequency: the sampling frequency must be two times or more than two times to the maximum frequency of the sampled signal According to the previous analysis of the traditional sampling mechanism, we can find that if the requirements do not meet, the subsequent signal reconstruction of the signal will be mixed, it named the signal distortion.
In Fig. 3, the length of the observed value is one fifth of the original signal length, which means the sampling frequency of the compressed sensing is one fifth of the traditional sampling frequency. It realizes the undersampling of signals. Through the quantization error contrast before and after the signal reconstructed in time-frequency domain, it proves that the sampling signal can make approximately accurate reconstruction.
5. Conclusions
Selecting Gaussian random observation matrix and Orthogonal Matching Pursuit algorithm (OMP) can realize approximately accurate reconstruction of the one-dimensional vibration signal. Through simulate signal compression sampling we can see that the sampling frequency of the compressed sensing signal is one fifth of the traditional sampling frequency, the characteristic parameter error between the original signal and the reconstructed signal in the time domain is less than 7 %, while the main frequency component in the frequency domain is not changed, using norm-2 to evaluate the error of reconstruction is only 1.71022, which can satisfy the engineering demand.
References
-
Candè E. J., Wakin M. B. An introduction to compressive sampling. IEEE Signal Processing Magazine, Vol. 25, Issue 2, 2008, p. 21-30.
-
Baraniuk R. G., Cevher V., Duarte M. F., et al. Model-based compressive sensing. IEEE Transactions on Information Theory, Vol. 56, Issue 4, 2010, p. 1982-2001.
-
Afonso M. V., Bioucas-Dias J. M., Figueiredo M. A. Fast image recovery using variable splitting and constrained optimization. IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society, Vol. 19, Issue 9, 2010, p. 2345-56.
-
Peng C., Wu E. X. Accelerating phase-encoded proton MR spectroscopic imaging by compressed sensing. Journal of Magnetic Resonance Imaging, Vol. 41, Issue 2, 2015, p. 487-495.
-
Candes E., Romberg J., Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, Vol. 52, Issue 2, 2006, p. 489-509.
-
Baraniuk R. G. Compressive sensing. IEEE Signal Processing Magazine, Vol. 24, Issue 4, 2007, p. 118-121.
-
Candes E., Tao T. Near optimal signal recovery from random projections: universal encoding strategies. IEEE Transactions on Information Theory, Vol. 52, Issue 12, 2006, p. 5406-5425.
-
Baraniuk R., Davenport M., Devore R., et al. A simple proof of the restricted isometry property for random matrices. Constructive Approximation, Vol. 28, Issue 28, 2015, p. 253-263.
-
Mallat S. G., Zhang Z. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing, Vol. 41, Issue 12, 1993, p. 3397-3415.
-
Tropp J. A., Gilbert A. C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory, Vol. 53, Issue 12, 2007, p. 4655-4665.
-
Donoho D. L., Tsaig Y., Drori I., et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Transactions on Information Theory, Vol. 58, Issue 2, 2006, p. 1094-1121.
