Abstract
When bearing vibration of instruments is monitored, a large number of data are produced. This requires a massive capacity of storage and high bandwidth of data transmission whereby costs and complex installation are concerned. In this study, we aim to propose an effective framework to address such the amount of bearing signals to which only meaningful information is extracted. Based on the compressed sensing (CS) theory. We proposed a reconstruction algorithm based on the multiple side information signal (RAMSI) with a purpose to effectively obtain important information from recorded bearing signals. In the process of sparse optimization, the RAMSI algorithm was implemented to solve the minimization problem with the weighting adaptive multiple side information signals. Wavelet basis and Hartley matrix were applied for the reconstruction process, for which the effective sparse optimization processing of bearing signals was able to adaptively computed. The performance of our RAMSI-based CS theory was compared with the basis pursuit (BP) which is based on the alternating direction method of multiplier (ADMM) and orthogonal matching pursuit (OMP). The error indices of the reconstruction algorithms were evaluated. This proves that the performance of the sparse optimization algorithm from our proposed framework is superior to the BP based on the ADMM and OMP algorithm. After recovering vibration signals, some strong noise caused by the incipient fault characteristic of the bearing. The complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) method was performed to extract the bearing fault component from such noise. In terms of performance, the CEEMDAN method was compared to the standard ensemble empirical mode decomposition (EEMD) method. The results show that the CEEMDAN method yields a better decomposition performance and is able to extract meaningful information of bearing fault characteristic.
1. Introduction
Long-term monitoring of rotating machinery can help early warning for safety and maintenance cost. This also guarantee for a normal operation for important machinery [1-3]. However, online monitoring of rotating machinery normally generates a large number of data, which could produce heavy loads on acquisition devices [4-6]. Therefore, methods to practically compressing data are crucial for cost-effective purpose and for an optimal control process in industrials.
The Compressed sensing (CS) theory has been widely applied to massive sampling data, which is able to break through the limitation of the Nyquist-Shannon sampling rule. The CS theory can effectively reconstruct signals with a small number of meaningful data, so as to alleviating a process of storage and transmission, which is suitable for long-term health monitoring of the rotating machinery [7-9].
The CS theory has been used in many areas, such as image and signal processing. The CS theory is combined with reconstruction algorithms for dealing with the minimum norm problem, resulting in realized reconstructed signals. Based on CS theory, the parallel FISTA algorithm is proposed for construction of vibration bearing, and Orthogonal matching pursuit (OMP) based on CS theory can be used to extract meaningful transient representation of bearing vibration signals [10, 11]. Furthermore, the k-means singular value decomposition algorithm was proposed to solves the sparse atom problem regarding the gear fault diagnosis, but there exists and issue when tackling a large number of collected signals [12, 13].
Besides, the alternating direction method of multiplier (ADMM) has shown its advantages of decomposition ability and convex optimization solution. Such method is beneficial to signal processing and statistical fields [14-16]. the ADMM also exhibits a good performance when applied to vibration signals. However, the characteristic of such signals is usually nonlinear and non-convex, so the ADMM algorithm should be improved for vibration signals [17, 18].
In order to improve quality of the recovering signals, we try to use different method, prior information theory of a signal side is introduced to satisfy the quality, which can deal with the measurement constraint. Meanwhile, signal side of prior information whereby weights are included can further improve the performance of the CS. The weights are determined by dividing the frame of the source signal into two sets with specific probability to ensure that signal recovery exists. This can also improve the reconstruction performance of sparse signals. So here, multiple prior signals method can replace the one prior signal, which can further reconstruct a spare signal, so the reconstruction algorithm with the multiple side information signal (RAMSI) based on the CS with weighing extension was proposed. The RAMSI algorithm takes advantage from the side information signals to reconstruct signals [19, 20].
In a real-world scenarios, the rotating machinery works under complex noise conditions, so it is necessary to decompose the rotating machinery fault information from such strong noise. Generally, wavelet transform (WT) has been applied to extract the fault characteristic information from the hybrid vibration signals [21]. However, the drawback of the WT is that the pre-set wavelet basis may lead WT to incompletely self-adaptive results when applied to non-stationary vibration signals. In this case, the Empirical Mode Decomposition (EMD) method is much more suitable to decompose such nonstationary signals into several intrinsic mode functions (IMF) [22]. Based on local characteristic time scale of the analyzed signals, the EMD show a strong adaptive ability for the vibration signals. However, the mode mixing is still the main drawback of the EMD method. An improved ensemble EMD (EEMD) was proposed to overcome the mode mixing issue, while decomposed IMFs represent residual noise [23]. Moreover, the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) was proposed to detect the fault diagnosis of rotating machinery from the hybrid signal.
According to the advantages of the ADMM, OMP and RAMSI approaches as described above, a new framework based on such algorithms for vibration signals analysis can make it possible. In this study, the basis pursuit (BP) based on ADMM is first described. We then introduce the RAMSI algorithm and how to apply three methods: (i) RAMSI, (ii) BP based on ADMM and OMP algorithm to vibration signals recorded from an actual operation of a bearing. The reconstruction errors were measured and discussed in the conclusions. Finally, the CEEMDAN is introduced to analyze the fault diagnosis characteristic of the bearing experiments.
2. The basis pursuit (BP) based on alternating direction method of multiplier (ADMM) algorithm
ADMM algorithm is usually utilized for a decomposition of several simple sub-problems and then solves them to obtain results. The ADMM method therefore has an advantage of solving composite problems. In order to improve the reconstruction performance of the ADMM algorithm, a small number of data points should be processed to recover important information, whereby the -norm minimum should be conversed to the -norm minimum solution. The ADMM algorithm is described as follow:
where and are described as convex functions, the vector variables , , and such functions are combined with the augmented Lagrangian, where , , and , a sparse optimal problem can be written as follows:
where , , and the augmented Lagrangian parameter . The Lagrangian minimization is derived as the basis pursuit formula for the ADMM algorithm, which has an advantage for optimizing distributed convex vectors with a number of iteration of the basis pursuit (BP). The formula is carried out into three steps as Eq. (3):
When dealing with a composite problem, the iteration mainly includes three steps: firstly and are fixed, and then minimize augmented Lagrangian with ; the second step is the same loop procedure but with the fixed values of and and the minimize augmented Lagrangian with respect to ; and the third step, is updated until the decomposition satisfies the stopping criterion.
3. The reconstruction algorithm with the multiple side information signal (RAMSI) recovery algorithm with multiple prior information
The RAMSI approach can be applied for recovering original signal from low dimensional measurement data with their prior information. When implementing the reconstruction algorithms based on the CS theory, the correlation across multiple prior information is leverage and results in an improvement quality of the sparse reconstruction. The RAMSI algorithm can overcome a shortcoming of one prior information by exploiting multiple previous information. The RAMSI method can be described as Eq. (4):
where and are diagonal matrices, the measured vector combined with the multiple prior information, is derived to be the -norm function and formulated the objective function as Eq. (5):
The objective function with multiple prior information evolves from the minimization of one prior information, whereby the minimization deals with the problem . The difference is that the computation of and the updated yield an optimal solution for the objective function for which multiple side information is applied to improve reconstruction quality. However, a decrease in correlation between the target signal and its prior information can occur which could lead to the problem of recovery degradation. Therefore, in the RAMSI approach, a multiplication of the weight parameters at each iteration is facilitated as Eq. (6):
where the th element of is defined as . When the multiple side information is fixed, it becomes crucial to choose , which affects the recovery of the original signal . Besides, when updating , different strategies should be applied to solve the constraint where is assigned. The value of is required attention when it is at a very low values. This produce a high value of which means that a strong the correlation is produced which is suitable for the recovery of the signal. Meanwhile in order to avoid function Eq. (6) breakdown when is zero, the parameter is applied to Eq. (6). If and the constraint , we can then obtain the as Eq. (7):
and the weight parameter can be written as Eq. (8):
where can be calculated from the function , and is given by:
For which Eq. (10a) and (10b) are described as follow:
and where by a boolean function is defined as follow:
Finally, the relative variation of is chosen as the stopping criteria.
Table 1Algorithm 1: The propose RAMSI algorithm
Input: , , , ,…, ; Output: ; Initialization: ; ; ; ; ; ; ; While Stopping criterion is false do ; ; ; Where is given by Eq. (9) // Updating weights. ; // Updating values for next iteration ; ; End Return |
4. Sparse optimization algorithms for bearing vibration signals
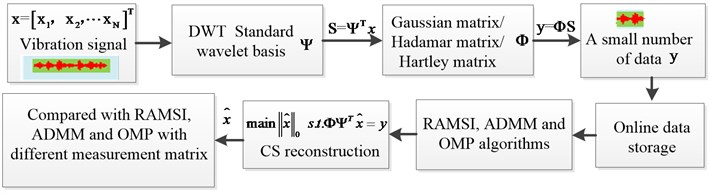
In this study, different sparse optimization algorithms are compared to each other for evaluating their performance with vibration signals recorded from bearing operations as input of the system. An effective framework is proposed to achieve sparse recovery of such vibration signals. Error analysis for indices of recovery bearing vibration signals was also examined for different sparse optimization algorithms. Based on the CS algorithm, the framework combined with the different algorithms is shown in Fig. 1.
A sparse representation, measurement and optimal reconstruction were mainly established as the procedures of the framework. Before comparing the performance among the three algorithms: the RAMSI algorithm, the OMP algorithm and the BP based on ADMM algorithm, the adaptive measurement were implemented in the framework. As sparse characteristic of the vibration signals recorded from a bearing operation is inexistent, so we were able to use the wavelet basis to process such vibration signals The three wavelet basis were selected as adaptive features for the proposed framwork. The Gaussian matrix, the Hadamar matrix and the Hartley matrix were performed to achieve a large sparse signal compression which results in a small number of data points with essential information. As the Gaussian matrix, the Hadamar matrix and the Hartley matrix indicate the incoherent characteristic of the analyzed signals. These matrices are then combined with the wavelet basis to form an adaptive measurement matrix, which also satisfy the restricted isometry property (RIP). The performance of the adaptive measurement matrix therefore was improved in terms of its accuracy. After compressing the signals, appropriate approach among the three algorithms: the RAMSI, BP base on ADMM and OMP algorithms were selected as the reconstruction algorithm. This can achieve the goal for obtaining meaningful signals with a small number of data points.
Fig. 1The proposed framework for vibration signal analysis. The framework is based on implementing the compressed sensing (CS) and RAMSI, ADMM and OMP algorithms
To validate the sparse recovering performance of the proposed framework. An examination among the three reconstruction algorithms with different measurement matrix, analyses the crucial indices were conducted. Here experimental data of the bearing signals were used as inputs of the proposed framework, the platform to generate vibration signals is described in Fig. 2. The experimental study and data collection were referred to Case Western Reserve University [3]. In this experiment, we chose the 6205-2RS JEM SKF bearings for obtaining vibration signals. The load 2.3 kW motor and the 40-mm pitch diameter of the ball group were used. The speed of the motor was set to 1750 rpm while the load was selected as 2 Hp. The vibration signals were acquired and sampled at 12 kHz.
Fig. 2The system of bearing vibration used in experiments.
To evaluate the performance of the proposed framework, 1024 data points of the recorded vibration signals were extracted. This results in sparse elements which were then compressed by both the wavelet basis and the Gaussian matrix. Optimal algorithms were then employed to reconstruct the recovering signals through the three algorithms: RAMSI, BP base on ADMM and OMP. The results from a reconstruction of different sparse optimal algorithms are indicated in Fig. 3. After reconstruction, we examined the performance of the three algorithms: RAMSI, OMP and BP based on ADMM by illustrating. the distribution diagrams of the recovering signals errors shown in Fig. 4.
From the computing of standard deviation and probability distribution of the reconstruction errors, the RAMSI algorithm shows smallest error which means the performance of the RAMSI yields the best performance among the three algorithms. After that, the specific quantitative indices were employed to evaluate the quality of the recovering precision shown in Table 2. The three performance indices: absolute mean, RMSE and SNR were computed from the results based on the RAMSI algorithms which give the values of 0.076, 0.107 and 12.740 respectively. For the BP based on ADMM algorithm, the three performance indices are 0.121, 0.156 and 9.478 respectively. Lastly, for the OMP algorithm, the three values are 0.193, 0.256 and 5.196, respectively. This proves that the sparse recovering performance of the RAMSI algorithm is the best.
Fig. 3The reconstructed signals resulting from the three sparse optimal algorithms based on Gaussian matrix: a). OMP algorithm; b) BP algorithm based on ADMM; c) RAMSI algorithm
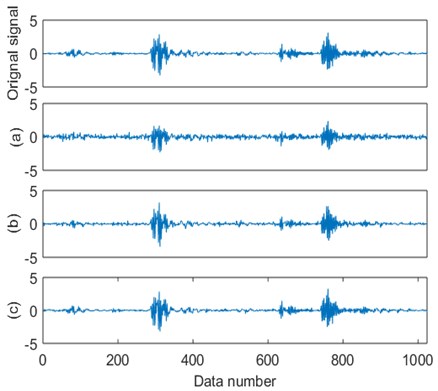
Fig. 4The errors distribution diagram based on the three different sparse optimal algorithms
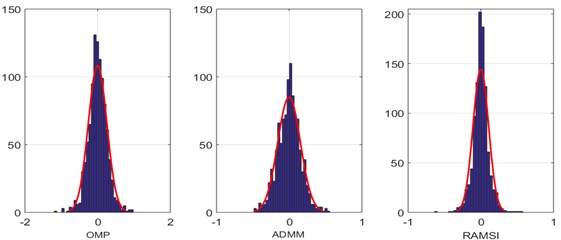
Table 2The comparison among the three algorithms: RAMSI, BP base on ADMM and OMP
Algorithm | Absolute mean | RMSE | SNR |
OMP | 0.193 | 0.256 | 5.196 |
BP | 0.121 | 0.156 | 9.478 |
RAMSI | 0.076 | 0.107 | 12.740 |
To improve the recovering performance of the RAMSI algorithm, the Gaussian matrix, the Hadamar matrix and the Hartley matrix were employed for the measurement matrix. In Fig. 5, the three measurement matrices are depicted using the 3d contour maps. We analyzed the density and stratification from the maps. When the three measurement matrices have the same number, it is found that the Hartley matrix yields the highest number of layers and sparse density. This means that the incoherence characteristics of the Hartley matrix is stronger than the Gaussian matrix and Hadamar matrix.
Furthermore, in order to evaluate the influence performance of the three measurement matrices based on the results performed by the reconstruction algorithm, the 1024 sparse data points were employed. By applying the wavelet basis, the sparse signals were then compressed using the Gaussian, Hadamar and Hartley matrices respectively. The RAMSI algorithm was then used to recover such compressed signals as illustrated in Fig. 6. After this process, the reconstructed signals were analyzed their recovering performance using the Gaussian, Hadamar and Hartley matrices, the errors of recovered signals were obtained by a distribution diagram shown in Fig. 6.
Fig. 5Three measurement matrices: a) Gaussian matrix, b) Hadamar matrix and c) Hartley matrix
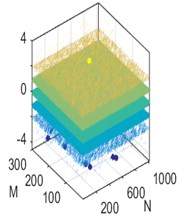
a)
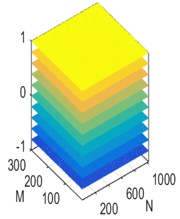
b)
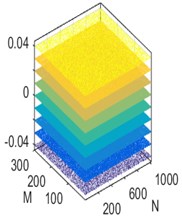
c)
Fig. 6The reconstructed bearing signals using the RAMSI based on the three measurement matrices, a) Gaussian matrix, b) Hadamar matrix and c) Hartley matrix
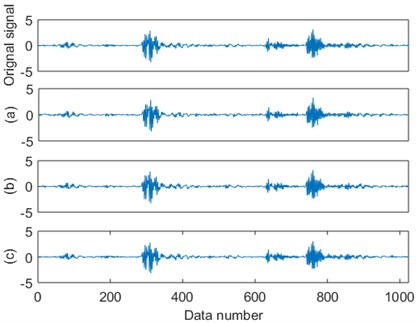
The reconstruction errors of the RAMSI approach based on different measurement matrices were evaluated through the distribution diagram. It is found that the analyzed results from each measurement matrix has influence on recovering performance of the RAMSI method. From the computed standard deviation and probability distribution, the Hartley matrix shows the smallest error. This means that the performance of Hartley matrix is better than both the Gaussian and Hadamar matrices. Besides, the specifically quantitative indices were used to assess the quality of recovering precision depicted in Table 3. The three values: absolute mean, RMSE and SNR computed computed using the Hartley matrix are 0.042, 0.059 and 17.99, respectively, while the three values computed using the Gaussian matrix are 0.076, 0.107 and 12.740, respectively and lastly the three values computed using the Hadamar matrix are 0.057, 0.079 and 15.425, respectively. This can prove that the sparse recovering performance of the RAMSI based on the Hartley matrix yields the best performance among the Gaussian and Hadamar matrices.
Table 3The comparison of recovering performance among the three matrices: Gaussian, Hadamar and Hartley
Measurement matrix | Absolute mean | RMSE | SNR |
Gaussian matrix | 0.076 | 0.107 | 12.740 |
Hamada matrix | 0.057 | 0.079 | 15.425 |
Hartley matrix | 0.042 | 0.059 | 17.990 |
Fig. 7The errors distribution diagram based on the three measurement matrices resulting from applying the RAMSI approaches to the recorded bearing signals, a) Gaussian matrix; b) Hadamar matrix and c) Hartley matrix
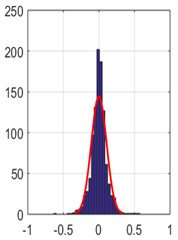
a)
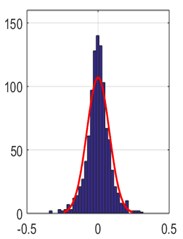
b)
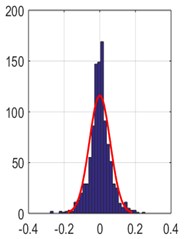
c)
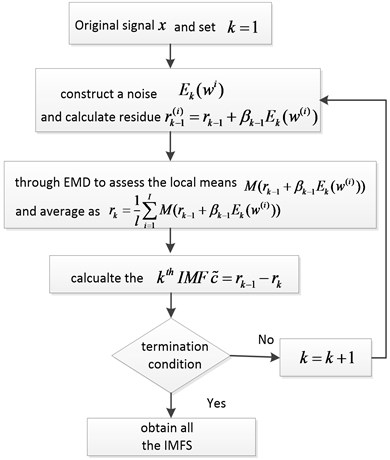
5. The CEEMDAN method
The performance of the CEEMDAN and EEMD methods was compared whereby for the CEEMDAN, the white Gaussian noise was replaced by the particular noise This particular noise was applied to extract the decomposed th IMF based on the EMD algorithm. In summary, the CEEMDAN method can be described as follows:
Step 1. Construct a particular noise and obtain , where is the original signal and is the th white noise.
Step 2. Calculate the local means for each and average all the determined local means for the first residual , and then, extract the the first IMF (for the first iteration) from .
Step 3. Calculate the second residual and the second IMF as performed in step 2.
Step 4. For the th, each number of IMF, is derived from the , where , .
Fig. 8Flow of the CEEMDAN method.
In order to demonstrate the effectiveness of the CEEMDAN method, the vibration signals were employed to examine the performance of both the EEMD and CEEMDAN methods Decomposed IMF signals and their frequency spectra were decomposed as shown in the Fig. 9 and Fig. 10.
Fig. 9a) The decomposed IMFs of the recorded vibration signal using the EEMD method, b) frequency responses of each decomposed IMF
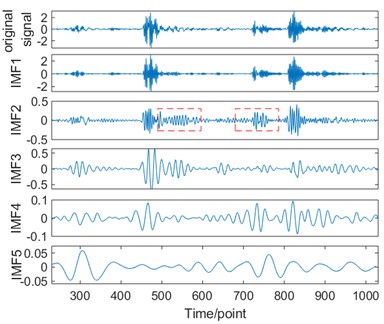
a)
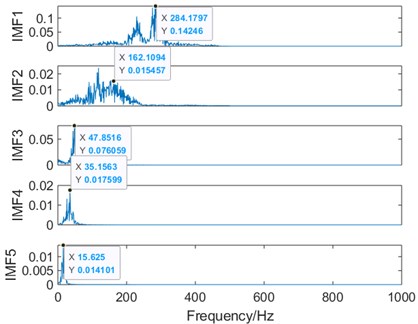
b)
Fig. 10a) The decomposed IMFs of the recorded vibration signal using the CEEMDAN method, b) frequency responses of each decomposed IMF
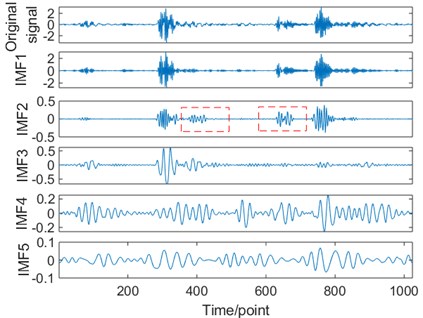
a)
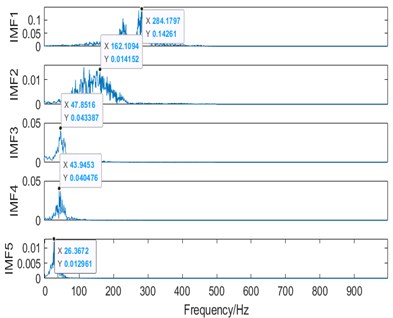
b)
For the EEMD method, the frequency spectra of the decomposed IMF#1 to IMF#3 are shown in Fig. 9(b) whereby their peak frequencies are at 284.18 Hz, 162.11 Hz, 47.85 Hz respectively.
For the CEEMDAN method, frequency spectra of the decomposed IMF#1 to IMF#3 are shown in Fig. 10(b) whereby their peak frequencies are at 284.18 Hz, 162.11 Hz, 47.85 Hz respectively. Besides, when the decomposed IMF2 signals of both algorithms in terms of frequency spectrum, it can be seen that the EEMD method was unable to reduce the residual noise, while CEEMDAN method can tackle this residual noise satisfactorily.
6. Conclusions
In this study, an adaptive hybrid model has been proposed in analysing vibration bearing for a long period of recordings. In which a large number of data are collected. Based on the compressed sensing theory and the sparse wavelet basis, we selected the Hartley matrix for compression. We then facilitated the RAMSI algorithm for reconstructing the compressed signals. The results from experiments have proved that the proposed framework yield high performance for vibration signals generated from bearing. Moreover, we have found some important facts based on implementation of our proposed framework as follows:
1) As the RAMSI has shown an advantage of exploiting the correlation and multiple prior information characteristic of the vibration signals, the framework therefore can overcome the shortcoming of one prior information and improve the quality of the recovered signals. Furthermore, compared with the BP based on ADMM and the OMP algorithms, the RAMSI algorithm has shown the minimum errors with the highest signal noise ratio (SNR). Therefore, the proposed RAMSI algorithm yields the best recovering performance.
2) In order to improve the recovering quality of the RAMSI algorithm, the Hartley matrix was selected as the measurement matrix, such matrix exhibits stronger incoherence characteristic compared to that using both the Gaussian and Hadamar matrices.
3) In terms of selecting a suitable decomposition approach, it is found that the CEEMDAN method can reduce the residual noise questions and extract the fault characteristics compared to the traditional EEMD method.
References
-
Chen B. J., Shen B. M., Chen F. F., et al. Based on integration of RSSD and wavelet transform to rolling bearing. Measurement, Vol. 131, 2019, p. 400-411.
-
Ahmed H. O. A., Wong M. L. D., Nandi A. K. Intelligent condition monitoring method for bearing faults from highly compressed measurements using sparse over-complete features. Mechanical Systems and Signal Processing, Vol. 99, 2018, p. 459-477.
-
Smith W. A., Randall R. B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mechanical Systems and Signal Processing, Vol. 64, Issue 65, 2015, p. 100-131.
-
Tu X. T., Hu Y., Li F. C., et al. Demodulated high-order synchrosqueezing transform with application to machine fault diagnosis. IEEE Transactions on Industrial Electronics, Vol. 66, Issue 4, 2019, p. 3071-3081.
-
Abedi M., Sun B., Zheng Z. A sinusoidal-hyperbolic family of transforms with potential applications in compressive sensing. IEEE Transactions on Image Processing, Vol. 28, Issue 7, 2019, p. 3571-3583.
-
Shao H. D., Jiang H. K., Zhang H. Z. Rolling bearing fault feature learning using improved convolutional deep belief network with compressed sensing. Mechanical Systems and Signal Processing, Vol. 100, 2018, p. 743-765.
-
Qiang W., Peilin Z., Chenet M., et al. Multi-task Bayesian compressive sensing for vibration signals in diesel engine health monitoring. Measurement, Vol. 136, 2019, p. 625-635.
-
Si L., Wang Z. B., Tao C., et al. A feature extraction method based on composite multi-scale permutation entropy and Laplacian score for shearer cutting state recognition. Measurement, Vol. 145, 2019, p. 84-93.
-
Luo B., Wang H. T., Liu H. Q., Li B., et al. Early fault detection of machine tools based on deep learning and dynamic identification. IEEE Transactions on Industrial Electronics, Vol. 66, Issue 1, 2019, p. 509-519.
-
Hou F. T., Chen J., Dong G. G. Weak fault feature extraction of rolling bearings based on globally optimized sparse coding and approximate SVD. Mechanical Systems and Signal Processing, Vol. 111, 2018, p. 234-250.
-
Bouchain A., Picheral J., Lahalle Blade vibration study by spectral analysis of tip-timing signals with OMP algorithm. Mechanical Systems and Signal Processing, Vol. 130, 2019, p. 108-121.
-
Lederman G., Chen S., Garrett J. H., Et At Track monitoring from the dynamic response of a passing train: A sparse approach. Mechanical Systems and Signal Processing, Vol. 90, 2017, p. 141-153.
-
Huang W. T., Sun H. J., Luo J. N., Et At Periodic feature oriented adapted dictionary free OMP for rolling element bearing incipient fault diagnosis. Mechanical Systems and Signal Processing, Vol. 126, 2019, p. 137-160.
-
Bouguezel S., Ahmad M. O., Swamy M. N. S. Binary Discrete Cosine and Hartley transforms. IEEE Transactions on Circuits and Systems I: Regular Papers, Vol. 60, Issue 4, 2013, p. 989-1002.
-
Skripnikov A., Michailidis G. Joint estimation of multiple network Granger causal models. Econometrics and Statistics, Vol. 10, 2019, p. 120-133.
-
Ramaswami S., Kawaguchi Y., Takashima R., et al. ADMM-based audio reconstruction for low-cost-sound-monitoring. 25th European Signal Processing Conference (EUSIPCO), 2017.
-
Peng G. J. Adaptive ADMM for dictionary learning in convolutional sparse representation. IEEE Transactions on Image Processing, Vol. 28, Issue 7, 2019, p. 3408-3422.
-
Zhang H., Chen X. F., Du Z. H., et al. Kurtosis based weighted sparse model with convex optimization technique for bearing fault diagnosis. Mechanical Systems and Signal Processing, Vol. 80, 2016, p. 349-376.
-
Luong H. V., Seiler J., Kaup A., et al. A reconstruction algorithm with multiple side information for distributed compression of sparse sources. Data Compression Conference (DCC), 2016.
-
Luong H. V., Deligiannis N., Seiler J. Sparse signal recovery with multiple prior information: Algorithm and measurement bounds. Signal Processing, Vol. 152, 2018, p. 417-428.
-
Lei Y. G., Liu Z. Y., Ouazri J., et al. A fault diagnosis method of rolling element bearings based on CEEMDAN. Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, Vol. 231, Issue 10, 2017, p. 1804-1815.
-
Guo T., Deng Z. M. An improved EMD method based on the multi-objective optimization and its application to fault feature extraction of rolling bearing. Applied Acoustics, Vol. 127, 2017, p. 46-62.
-
Mohanty S., Gupta K. K., Raju K. S. Vibro-acoustic fault analysis of bearing using FFT, EMD, EEMD and CEEMDAN and their implications. Advances in Machine Learning and Signal Processing. Lecture Notes in Electrical Engineering, Springer, Cham, Vol. 387, 2016.
Cited by
About this article
The research is supported by the Natural Science Foundation of Shanghai (Grant No. 19ZR1463800), the Subject of Science and Technology on Micro-system Laboratory, Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences (Grant No. 6142804190206).
