Fault diagnosis and health management of bearings in rotating equipment based on vibration analysis – a review

2.1.1.1. Mean and standard deviation

Obtained signals can be described using parameters such as standard deviation ($\sigma$) or the mean ($\mu$). Numerically, the mean value is the sum of the events divided by the number of events. [17]. The standard deviation is a tool used for measuring the dispersal in a certain signal. Mathematically, it is the variance under the square root, see Eqs. (1) and (2) [17]. For an event ($X_i$) and size of sample ($N$), $\mu$ and $\sigma$ are calculated using the following equations respectively:

2.1.1.2. RMS

RMS is concerned with the energy of the vibration signal and is suitable for the detection of deteriorating bearings, however, the initial peaks in the signal at the beginning stages of the fault cannot be detected using RMS, furthermore, RMS is not suitable for identifying the location of the fault. However, RMS is suitable for measuring the severity of the fault. It is also worth noting that RMS is not sensitive to transient changes that can last for only milliseconds.

Detection with RMS considers the increase in the value of the vibration signal against a normal operations signal. RMS is calculated as follows:

$A$ represents sample amplitudes of the vibration signal.

Seryasat et al. [18] presented a method for diagnosing bearing faults using RMS and FFT, the RMS of the vibration signal changes for different frequency bands when the fault occurs, thus the method was tested using faulty bearings at various loads and speeds whereby the RMS indicates the type of the fault.

2.1.1.3. Kurtosis

The Kurtosis technique is sensitive to impulsiveness and can detect vibration signals associated with faults in their early stages [12]. Kurtosis is calculated as follows:

where $y_i$ denotes the instant amplitude, $y^{-}$ represents the mean and $\sigma$ is the standard deviation of the data and $n$ is the length of the sample.

Spectral kurtosis analysis is used to identify the energy content of decomposed signals [19]. The main disadvantage of kurtosis is that it cannot detect the fault at the later stages. Tian et al. [20] presented a method for detection of bearing faults using spectral kurtosis with cross-correlation, they extracted features that represent faults which are combined to create an index using principal component analysis (PCA) and $k$ – nearest neighbour (KNN), their method successfully detected incipient faults and identified the location, importantly, it was able to provide a health index to track the degradation of faults. Saidi et al. [21] use a spectral kurtosis data-driven approach for health prognosis of shaft bearings, the method was validated using monotonicity and trendability and real data from a wind turbine drivetrain and it was shown that the method could detect the early failure and improve the estimation of degradation. Liao et al. [7] extract repetitive transients by using frequency domain multipoint kurtosis to diagnose bearing faults, computational accuracy was improved through redefining the kurtosis in the frequency domain.

2.1.1.4. Crest factor

The CF is defined as the ratio of peak signal value to the RMS level, this indicator is frequently used to characterize vibration data. Values of CF for healthy bearings are typically in the range of 2.5 to 3.5, increasing when a defect is present [22]. Crest factor can be calculated using Eq. (5):

Reference after name “Heng and Nor [23] performed a comparative study using statistical parameters including CF and KU applied to the sound and vibration signals from bearings to assess their relative abilities to detect defects [ 23]. Their results confirmed that statistical methods may be employed to identify the type of defect in the bearings. Moreover, their results showed that there is no significant advantage in using more advanced beta function parameters applied to the vibration signals to identify faults in rolling element bearings than KU of CF.

2.1.1.5. Peak value

Peak value is the maximum value of the wave, from the average to the highest points is a simple measurement that shows when impacts happen and is useful for low level faults. Specifically, the peak values are observed throughout discrete sequential time intervals and then analysed, the analysis involves the peak values, the spectra from the peak value time waveform and the autocorrelation coefficient [3]. Wang et al. [24] use peak-based multiscale decomposition for fault detection in rolling element bearings. Their novel peak-based approach combines envelope demodulation with multiscale decomposition and was validated by using rolling bearing element faults and it was found to enhance fault features and detection.

2.1.1.6. Energy index

As mentioned above as the magnitude of the defect or fault develops the amplitudes of the CF and KU reduce back to more normal values. The Energy Index (EI) is a technique that is used to overcome this inadequacy. Al-Balushi et al., [25] have defined the EI as: “a ratio of the root mean square of the segment of the signal (RMS segment) to the overall root mean square (RMS overall) of the same signal” [25]. They successfully applied the EI technique to detect the presence of a defect in both simulated and experimental data for a bearing. EI can be calculated using Eq. (6):

We have explored various time-domain techniques to extract signal features and make condition assessments. Several of the presented techniques are available off-the-shelf. The simplicity of these techniques means they can often be computed in real time and can identify the moment at which a change to the time series takes place.

2.1.2.1. Fourier transform (FT)

Fourier transform is used for mapping the time-domain function into the frequency-domain [30, 31]. Today, the Fast Fourier transform (FFT) is a commonly used technique to obtain the frequency-domain signal from the time-domain. However, time information is lost in the process, so that the Fourier transform (FT) cannot indicate when a particular event occurred. Such a loss can be vital when exploring the growth of faults, because transient events can be the most important element in the signal.

In an attempt to make good this deficiency, Gabor [32] portioned the signal into contiguous sections (known as windows), so the FT analysed a small section of the signal each time [32]. The time-domain signal within each window was then transformed into the frequency-domain. Note that the time window acts as a multiplying function and must be tailored mathematically so as not to introduce bogus results [33].

An important characteristic of these windows is that their final and initial values are zero, or close to zero, to avoid the time signal appearing as a sequence of rectangular step functions. Today, a wide range of such windows is readily available. The Short-Time Fourier Transform (STFT) reveals a spectrum for each window. The time interval for each of the windows is known, so the individual spectra can be combined into a 3-D map with co-ordinates: frequency, time and amplitude.

This method has two shortcomings: (i) it is not possible to simultaneously have high-quality resolution in both frequency and time-domains because of the uncertainty principle, (ii) the duration of the window is fixed, once chosen it cannot be changed, but in many signals the frequency content does change with time, requiring greater precision at some times than others, [34]. Suppose the signal to be of brief duration, clearly a short window will be chosen, however, the shorter the window is the wider the corresponding frequency band and the less the resolution of the frequency.

Wavelet analysis has attracted extensive interest as a diagnostic tool for condition monitoring of bearings. The FT is limited to presenting the time-domain signal as sine and cosine functions, however, wavelet analysis can describe a signal for the entire spectrum of interest by using wavelet functions (WFs) of different, or variable, scales.

2.1.2.2. Envelope analysis

With envelope analysis, a high pass filter is employed to remove the lower frequencies from the high-frequency part of the spectrum [35]. As a result, envelope analysis can detect peaks that usually cannot be found in the noise carpet or noise floor [35]. Envelope analysis is recognised as a well-known algorithm for bearing fault analysis and Feng et al. [36] study several envelope techniques including spectral correlation, Hilbert transform and band-pass squared rectifier which showed similar levels of accuracy. In the case of a fault, such as a spall, each time the bearing passes over the spall there is a small click, the number of clicks and the rpm provide the clicks per minute on the FFT (fast Fourier transform). Here the click would normally be visible, however, the low-frequency part of the spectrum is crowded so it is not easy to identify smaller peaks. The envelope technique overcomes this by a process of modulation which takes the click frequency away leaving the trace which is at a lower frequency from which the envelope analysis identified the defective bearing [35]. Thus, through employing envelope analysis it is possible to amplify the fault frequencies through demodulation which reveals the envelope signal [37].

Fig. 1Signal and envelope signal from local bearing fault. Source: Randall and Antoni [37]

2.3.1.1. Artificial neural network

An artificial neural network (ANN) is essentially a model with a set of interconnected relationships between inputs and desired outputs. ANNs are based on the behaviour of the neural networks that are found in the human brain. As such an ANN can be considered as a machine learning system that contains neurons that form interconnected links between inputs and outputs for processing information. It is possible to train these connections.

More specifically, the ANN involves functions which include multiplication, summation and transfer. Multiplication is carried out by neurons by assigning a weighting to the inputs and then adding them together, the sum of the weights is the inputted to transfer function. Weights are changed automatically to improve compliance of the model in relation to the data [4]. Data-driven ways for machine learning in prognostics employ numerical algorithms including neural networks [44] and a popular data-driven method is artificial neural networks.

However, ANN models are not suitable for constant and rapid fluctuations found in a system [38]. Thus, they are not suitable in this way and to improve prognosis models it is important to consider the physics of the wear evolution process where model-based approaches offer better results compared to data-driven approaches [38].

Dharmawan et al. [45] developed a fault diagnosis system for rotating machines using a combination of ANN and continuous wavelet transform (CWT). Feature extraction for the CWT involved putting the data into different types which included root mean square, kurtosis and power spectrum density as inputs for the ANN, their methods returned an accuracy for damage detection of 99.72 % [45]. Gomez et al. [46] developed an automatic condition monitoring system for detecting cracks in rotating machines, they combined ANN with Wavelets Packet transform together with Radial Basis Function which is applied to vibration signals, these additions to ANN optimised the success rate, returning close to 100 % probability of detection with 1.77 % false alarms. Beretta et al. [47] validate a method for predicting bearing faults based on an ensemble of an ANN.

2.3.1.2. Principle component analysis (PCA)

PCA analyses data using a multivariate technique to derive observations that are described by inter-correlated dependent variables [2]. PCA is essentially an algorithm that shows the data’s internal structure in a way that makes the variance in the data clear and explainable.

The use of PCA increases the accuracy of the fault diagnosis, this is where PCA identified features are used instead of the normal 13 features, where the increase in accuracy is from 88 % to 98 %. This efficiency is achieved with a limited amount of input features in comparison to using original features.

Where a dataset is multivariate and is seen as a set of coordinates that are found in a high-dimensional data space, the PCA will give the user a projection that has a lower dimension. The features of bearing defects are characteristically sensitive and may change due to different conditions, and PCA is an effective way for feature selection and it provides a way of manually choosing representative features for the purposes of classification. De Moura et al. [48] employed PCA and neural networks to investigate pre-processed signals from Detrended Fluctuation Analysis (DFA) and Rescaled-Range Analysis (RSA) in the detection of the severity of bearing faults. PCA and ANN were used for pattern recognition, however, it was determined in their study that pattern recognition from vibration analysis using PCA was inferior to that of ANN [48]. PCA models have been improved by incorporating two statistical process monitoring properties, namely, static and dynamic [49].

Mohanty and Raju [19] in averting bearing failure studied the vibration acoustics of ball bearings using a wavelet-Based Multi-Scale Principle Component Analysis with FFT. The algorithm derives the frequency range from the ball bearing operation which helps to determine the frequency of the vibration without the perplexing frequency components [19]. The main advantage that they gained from using this approach was that it allowed feature segmentation from the channels that were independent to the direction of the propagation of the bearing fault, essentially the PCA simultaneously auto-correlates and cross-correlates the signal [19]. Wang et al. [50] demonstrated a method for reliability assessment of rolling bearings using kernel principal component analysis, using this approach feature extraction is achieved using time, frequency, and time-frequency domains and it was found that using KPCA accurately reflected the performance of the degradation process.

2.3.1.3. K-nearest neighbours (k-NN)

k-NN is an algorithm that is a non-parametric way for classification or regression. Specifically, in this method, the class of an object is the output which is shown by a majority vote of the nearest $k$-neighbour. Early use of the k-NN algorithm has been used for data mining, furthermore, k-NN has also been used for distance analysis for each data sample to find out if it should belong to a certain fault class. Baraldi et al. [51] present a diagnostic system for detecting the beginning stages of fault degradation through isolation of the bearing and then classification of the defect, this system was based on a hierarchy of k-NN classifiers, the system was found to be satisfactory in diagnostic performance.

Wang et al. [52] proposed a real-time fault diagnosis system for predictive maintenance of rolling bearings using a k-NN algorithm. Their system used a pre-processed signal and feature parameter extraction thereafter training and optimisation of the fault diagnosis model and it was found that a diagnosis model that uses a k-NN algorithm was more effective than diagnosis based on other algorithms such as C.45 and CART and therefore, is suitable for predictive maintenance of rolling bearings [52].

Weighted $K$ nearest neighbour (WKNN) is a new methodology within k-NN developed by Sharma et al. [53]. It is a squared inverse feature weighting technique that improves the performance of the k-NN classifier and can optimise the computation complexity and classification accuracy [53].

Yan et al. [54] presented a hybrid intelligent fault diagnostic model for rolling bearings that combines a k-NN classifier with a stacked sparse auto-encoding network (SSAE). Their model used the advantage of the k-NN algorithm that it can deal with multi-classification problems and improve the accuracy of their model [54]. Overall, in comparison to traditional methods using deep neural networks for feature extraction avoids being overly dependent on professional knowledge and improves the accuracy of the fault classification [54].

2.3.1.4. Ensemble learning

Zhang et al. [55] predict RUL of rolling element bearings using ensemble learning which is considered to be a typical machine learning approach and has been promising in pattern recognition. However, this approach had been very rarely used for RUL and Zhang et al. [55] propose to achieve this through merging multi-piece information and then updating it dynamically.

In response to the problem of strong ambient noise interfering with the collection of bearing signals making it difficult to accurately identify faults, Liang et al. [56] presented an improved ensemble method using deep belief network (DBN), their method was shown to significantly improve the fault diagnosis.

To improve rolling bearing fault diagnosis Li et al. [57] presented an enhanced selective ensemble deep learning method. The ensemble learning was implemented using enhanced weighted voting together with class-specific thresholds and the results showed that their method was more accurate and more robust in recognising the different types of faults in comparison to other ensemble learning methods [57].

Table 1Summary of machine algorithms – classical methods – architecture, description and characteristics

Architecture	Description and characteristics
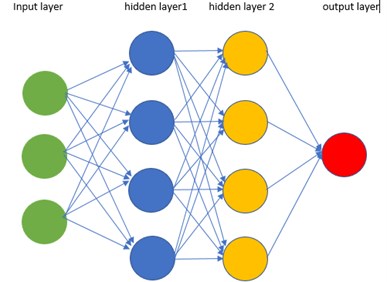	Artificial Neural Network – Based on behaviour of neural networks in human brain – Uses multiplication, summation and transfer functions Pros: – Can learn independently – Input is stored in network and not on database Cons: – Not suitable for constant and rapid fluctuations
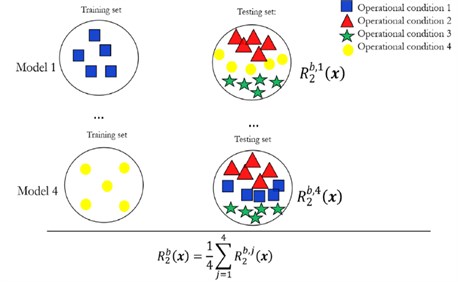Baraldi et al. [51]	K Nearest Neighbour (KNN) – Non-parametric method for classification and regression Pros: – Simple and easy to implement – Does not require offline training Sharma et al. [53]
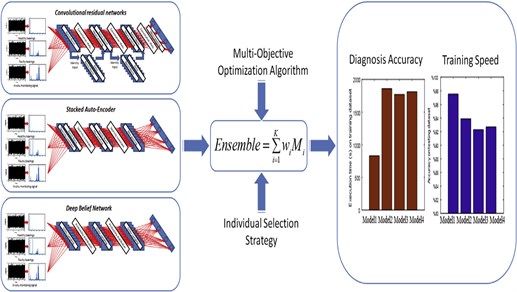Ma and Chu [58]	Ensemble learning – Uses the advantages of each member model as an ensemble strategy Pros: – Promising for pattern recognition – Accurate and robust in recognising different types of faults – More adaptable than single deep methods
Abdi and Williams [2]	Principle Component Analysis (PCA) – Multivariate technique for analysing data tables – Describes intercorrelated quantitative dependent variables – Extracts important information from tables Pros: – Variance in the data is clear and explainable – Shows internal structure of data Abdi and Williams [2]

In response to the issue of there being a broad application of technology for fault diagnosis and the associated limitation of the application of a single deep model, Ma and Chu [58] proposed an ensemble deep learning diagnosis method using multi-objective optimisation which was shown to be more adaptable in comparison to other ensemble and single deep methods. Furthermore, Xu et al. [59] recognised that most fault diagnosis methods find it difficult to learn representative features from raw data. In response to this issue, Xu et al. [59] proposed that deep learning with its ability to perform automatic feature extraction should be combined with ensemble learning, in this case, random forest (RF) ensemble learning, due to its ability to improve generalisation performance and accuracy of classifiers.

2.3.2.1. Convolutional neural network (CNN)

Convolutional neural networks are inspired by animal visual cortices and were first used for the detection of image patterns hierarchically including simple and complex features. The lower layers will have lower level features, and higher levels will detect features that are higher level, built on the lower level features.

About the architecture of CNN, the one-dimensional temporal raw data is taken from the accelerometers and are stacked in a two-dimensional vector-like image representation before a convolutional layer conducts feature extraction, thereafter, down sampling takes place in the pooling layer. This convolution and pooling combination are repeated numerous times to make the network deeper. The output from hidden layers is passed to connected layers and the output is then passed to a top classifier based on Sigmoid or Softmax for bearing fault detection.

Xu et al. [59] propose a fault diagnosis method based on CNN and random forest ensemble learning and achieved a high level of accuracy in bearing fault diagnosis and was an improvement on standard deep learning methods and traditional methods. CNN can learn features automatically from the inputted data and has the potential to overcome traditional methods [62].

Belmiloud et al. [5] use CNN as part of their method for determining RUL of rolling element bearings. Specifically, extracted features are fed into a deep CNN to construct a health indicator. Hoang and Kang [62] propose a method for bearing fault diagnosis using CNN where vibration signals are used directly as input and therefore, there is no need for feature extraction. Their method was found to be highly accurate even in noisy environments [62]. Specifically, the method transformed 1-D vibration signals into 2-D images taking advantage of CNN effectiveness in image classification [62]. The issue of noise was also addressed by Zhao et al. [39] who said that diagnosis is difficult for planetary gearboxes due to planetary noise. They propose a diagnosis method using synchrosqueezing transform (SST) and deep CNN together with envelope time-frequency representations, their method automatically recognised the planet bearing fault type and also removed interference from the time-frequency spectrum effectively avoiding misdiagnosis [39].

The problem of traditional time or frequency domain analysis, in that they cannot extract features effectively, has been addressed by Zhang et al. [63] who introduce an enhanced CNN method using short-time Fourier transform, scaled exponential linear unit and hierarchical regularisation, the results of their experimentation showed that the method had higher accuracy of fault diagnosis than other deep learning methods [63].

Liu et al. [64] solve the problem of information losses when using the fusion process through an ensemble CNN model for diagnosing bearing faults, specifically, the model used one multi-channel fusion convolutional neural network branch and two 1 dimensional CNN branches, the former extracts features from sensory data and the latter extracts from the inherent features which reduces the loss of information, overall the model was found to be more effective and robust than other models [ 64].

2.3.2.2. Auto-encoders

Autoencoders have their origins in pre-training methods used for artificial neural networks. After years of development this approach has become popular as a method of feature learning, furthermore, it has been described as being a greedy layer-wise method for pre-training.

An ANN is used to train the auto coder which is comprised of an encoder and a decoder whereby the encoder’s output is the input for the decoder. The mean square error between input and output as the loss function is taken by the ANN to generate the output through imitation of the output. Once the ANN has been trained the decoder is discarded and the encoder is retained. This means that the feature representation is the output of the encoder, and it is this that is used in the classifier in the next stage.

However, although autoencoders was an early approach, more modern and state-of-the-art approaches are more focussed on deep neural networks with many layers that employ a backpropagation algorithm [5]. Haidong et al. [65] presented a novel method for intelligent bearing fault diagnosis using ensemble learning which analyses experimental vibration signals together with a combination strategy to achieve an accurate diagnosis. The results showed the method removes the need to depend on manual feature extraction and overcomes limitations associated with deep learning models [65].

2.3.2.3. Deep belief network (DBN)

In deep learning, a deep belief network (DBN) is considered as a compilation of unsupervised networks, for example, restricted Boltzmann machines or auto-encoders, whereby the hidden layer of each sub-network acts as a visible layer which is used to train the DBN. Furthermore, for SAE the fused features are inputs into the DBN for the classification of faults.

Deutsch [61] validated deep learning prognosis methods using big data collected from bearing test rigs to determine bearing RUL predictions. One of the methods used by Deutsch [61] was the Deep Belief Network. Specifically, the DBN was trained using FFT features and upon completion of training a fine-tuning layer was added to the DBN, the results were promising as the approach added robustness to the architectures and reduced the probability of poor results [61].

Shao et al. [66] propose a novel continuous deep belief network optimised with the use of a genetic algorithm in order to adapt the characteristics of signals, the proposed method was tested using bearings and it was found to be superior in terms of accuracy and stability than traditional methods. Shen et al. [67] recognise the limitations of diagnosis mechanisms that use manual feature extraction, as a solution deep learning can learn representative features in the data without the need for much prior knowledge. Shen et al. [67] presented a new method for bearing fault analysis named hierarchical adaptive DBN optimised by using the Nesterov momentum, their model was validated using vibration signals from bearings and it was found that the method shows more satisfactory performance than conventional DBN and support vector machine [67].

2.3.2.4. Recurrent neural network (RNN)

Data in the recurrent neural network method is processed in a recurrent behaviour as opposed to a feed-forward neural network. The flow path of this goes from the hidden layer back to the flow path when it is sequentially unrolled. Because it is a sequential model it can capture and model any sequential relationship that can be found in time series or sequential data [68].

A recent approach that used deep recurrent neural network (DRNN) was proposed by Jiang et al., [69] which used stack recurrent hidden layers as well as LSTM units, furthermore, an adaptive learning rate was also used to improve training performance. This approach returned high accuracy results of 94.75 % and 96.53 % [69]. Wu et al. [70] proposed a novel approach for fault prognosis using recurrent neural network, specifically, recurrent neural network was used with the degradation sequence of equipment, again with LSTM units, and showed significant performance in RUL prediction. Xie and Zhang [71] also recognised the beneficial potential of deep network neural algorithms, LSTM and recurrent neural network and proposed a novel approach for fault prognosis using LSTM based on the vibration signal of rotating equipment, the outcomes were successful in improving machine condition monitoring and health management.

2.3.2.5. Generative adversarial network (GAN)

Goodfellow et al. [72] first proposed GAN in 2014 and is comprised of two parts which are the generator $F_G$ and the discriminator $F_D$ which compete with each other whereby $F_G$ tries to confuse $F_D$ while the latter tries to distinguish samples generated by the former. They are competing with each other to gain increased capability for imitating the original data samples and then to discriminate iteratively.

Table 2Summary of machine algorithms – deep learning-based approaches – architecture, description and characteristics

Architecture	Description and characteristics
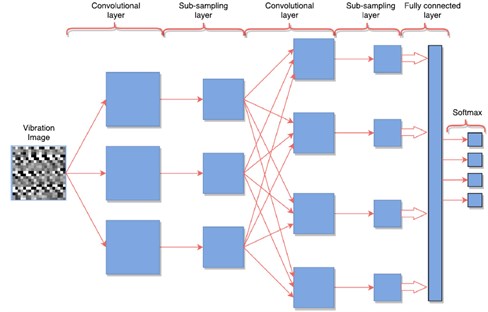Hoang and Kang [62]	Convolutional Neural Network – Based on animal visual cortices – Uses 2-D data – Has variations such as ADCNN, Lifting Net and inception net Pros: – Fewer neuron connections needed compared to normal ANN Cons: – Requires more layers to find a whole hierarchy Zhang et al. [63] – May need a large labelled dataset Zhang et al. [63]
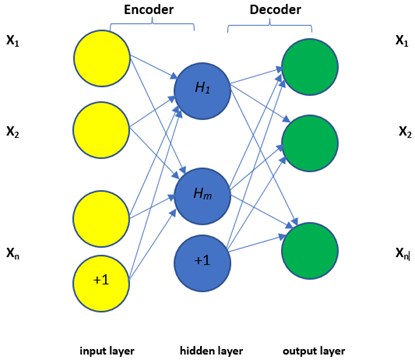	Auto Encoders – Used for feature extraction – An unsupervised learning method that reconstructs the input vector Yan et al. [54] Pros: – Does not need labelled data – Variants of autoencoders have an algorithm which is noise resilient Cons: – Requires pre-training – Training may suffer from the disappearing of errors Zhang et al. [63]
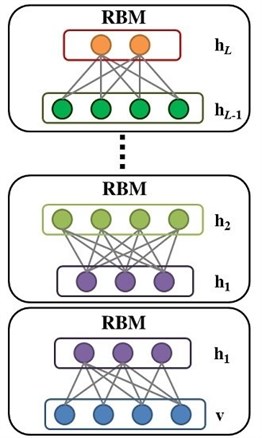Lin et al. [73]	Deep Belief Network (DBN) – Built with RBMs – each hidden layer is the visible layer for the next – Undirected connection at the top two layers – Training is supervised or unsupervised Zhang et al. [63] Pros: – Can use layer by layer learning strategy to start the network – The likelihood is maximised through tractable inferences Zhang et al. [63] Cons: – Training can be computer-intensive and expensive due to initialisation and sampling
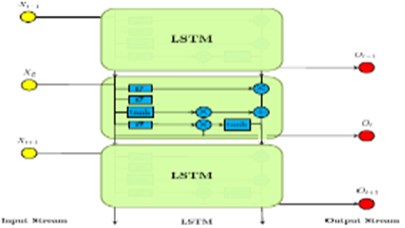Zhang et al. [68]	Recurrent Neural Network – Analyses 1-D temporal or sequential data – Used for applications where output independent on previous computation Zhang et al. [63] Pros: – Can memorise sequential events – Can model time dependencies – Can receive inputs of variable lengths Zhang et al. [63]
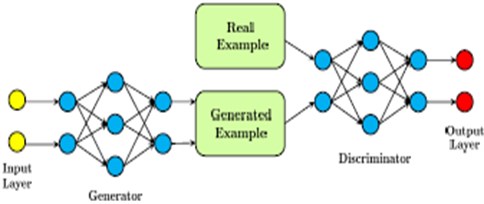Zhang et al. [68]	Generative Adversarial Network (GAN) – Uses a generator and a discriminator to generate images which imitate real photos – Augments data where labelled data is scarce Zhang et al. [63] Pros: – Does not need modification when moving to new applications – Does not have a deterministic bias Cons: – Training is unstable because requires finding Nash equilibrium – Difficult to learn how to create discrete data Zhang et al. [63]