Near-optimal pitch of a moiré grating for image hiding applications in dynamic visual cryptography

1. Introduction

Visual cryptography (VC) is a special encryption technique used to hide visual information in a way that it can be decrypted purely by the human visual system and no computational techniques are required. First introduced by Moni Naor and Adi Shamir [1] in 1994, VC is based on the division of the original image into several semi-transparent shares. Each share individually does not reveal the secret, but if all these shares are overlaid at the right position, a secret message appears [2]. Recently many advances have been done in visual cryptography: visual cryptography of gray-level and color images was introduced in [3]; probabilistic visual secret sharing scheme for grey-scale and color images was presented in [4]; letter-based VC scheme where pixels are replaced by letters in the share images was proposed in [5], sharing of multiple secrets in visual cryptography was discussed in [6]; security of visual cryptography schemes was analysed in [7-9].

Geometric moiré is a classical optical experimental technique based on analysis of visual patterns formed as a superposition of two regular gratings that geometrically interfere [10, 11]. Geometric moiré techniques can be extended to time-average geometric moiré methods. If moiré grating is formed on the surface of oscillating structure and time-averaging techniques are applied, pattern of time-averaged fringes emerges [12].

The concept of dynamic visual cryptography was first introduced in [13]. This method is based not on static superposition of shares like in VC, but on the time-averaging techniques applied for a single encoded image. The secret image is embedded into the moiré grating in such a way, that one pitch of the moiré grating is used to form the background of the secret image and a slightly different pitch of another moiré grating is used to represent the secret. Phase scrambling completely hides the secret and a naked eye cannot interpret the secret from the stationary cover image. The secret is decoded in a form of a pattern of time-averaged moiré fringe when the cover image is oscillated according to a predefined law of motion. Furthermore, the amplitude of the harmonic oscillations must be set to a preselected value in order to leak the secret. The security of the encoding and the sharpness of the decoded secret are mostly influenced by the selection of the pitches of moiré grating. Pitches of the grating representing the secret image and the background cannot differ very significantly – otherwise, encoded secret could be seen by a naked eye in a static share. At the same time, the difference between the pitches should ensure the sufficient contrast between secret and background areas in time-averaged image. This paper proposes scheme for the determination of near-optimal pitch of the moiré grating for image hiding in dynamic visual cryptography.

2. Optical background

One-dimensional harmonic moiré grating reads [10, 11]:

where $x$ is the longitudinal coordinate, $\lambda$ is the pitch of the moiré grating. The numerical value 0 of function $F\left(x\right)$ corresponds to black color, 1 – to white color, all values between 0 and 1 correspond to the appropriate greyscale levels.

Let us suppose that the moiré grating (Eq. (1)) is formed on the surface of one-dimensional non-deformable body and is harmonically oscillated around the state of equilibrium according to harmonic function: $a\cdot \mathrm{s}\mathrm{i}\mathrm{n}(\omega t+\phi )$, where $a$ is the amplitude of harmonic oscillations, $\omega$ is the frequency and $\phi$ is the phase. Then grey-scale level of moiré grating at coordinate $x$ at time moment $t$ can be expressed [12]:

Greyscale level of time-averaged geometric moiré can be obtained averaging Eq. (2) in time [12]:

where $T$ is the exposure time used for the time-averaging, $J_0$ is the zero order Bessel function of the first kind. Note, that oscillation frequency $\omega$ and phase $\phi$ have no influence on the formation of time-averaged image [11, 12]. Time-averaged image becomes continuously grey at the roots of $J_0\left(\frac{2\pi }{\lambda }a\right)$:

where $r_i$ is the $i$th root of the zero order Bessel function of the first kind.

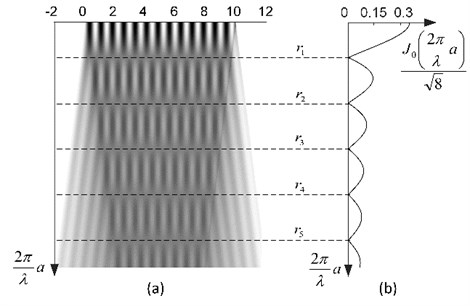
Fig. 1Time-averaged moiré at λ=0.75: a) one-dimensional time-averaged moiré in case of harmonic oscillations at increasing amplitudes a; b) standard deviation of time-averaged moiré

It can be noted, that standard deviation of time-averaged image, described by Eq. (3), is calculated as follows [14]:

Fig. 1(a) provides one-dimensional time-averaged moiré image at increasing amplitudes. It is clear that time-averaged fringes form at amplitudes corresponding to the Eq. (4). Fig. 1(b) shows the variation of the standard deviation of the time-averaged moiré at increasing amplitudes. Value of the standard deviation within the time-averaged image depends on a blur level in time-averaged moiré grating: sharp structure of the grating ensures sufficiently high standard deviation. Note that standard deviation is equal to zero at the centers of time-averaged fringes.

3. Estimation of near-optimal pitch of a moiré grating

The main idea of hiding a secret in the dynamic visual cryptography is to encode this secret image into moiré grating: one pitch of the moiré grating is used to form the background of the secret image and a slightly different pitch of another moiré grating is used to represent the secret. Let the pitch of the grating in the area of secret information be denoted ${\lambda }_s$, the pitch of the grating in the background – ${\lambda }_b$. Pitches of the grating ${\lambda }_s$ and ${\lambda }_b$ cannot differ very significantly $\left|{\lambda }_s-\mathrm{}{\lambda }_b\right|\le \epsilon$, otherwise the encoded secret could be seen by a naked eye in a static share. Simultaneously, the difference between ${\lambda }_s$ and ${\lambda }_b$ should ensure the sufficient contrast between secret and background areas in time-averaged image.

The secret information is leaked if only the cover image is oscillated harmonically. Secret appears as a uniformly grey area in time-averaged image while background contains slightly blurred pattern of the cover image.

Let the standard deviations of the secret and background areas in time-averaged image be denoted as ${\sigma }_s$ and ${\sigma }_b$ respectively. Values of ${\sigma }_s$ and ${\sigma }_b$ are calculated as [14]:

Sufficient contrast between the leaked secret and the background in the time-averaged cover image is obtained if only $\left|{\sigma }_s-\mathrm{}{\sigma }_b\right|\ge \delta$. The graphical representation of standard deviations ${\sigma }_s$ and ${\sigma }_b$ is proposed in Fig. 2.

Fig. 2Variation of standard deviations of time-averaged moiré. Thick solid line stands for standard deviation of the secret σs at λs=0.45; thin solid and thin dashed lines represent standard deviations of the background σb1 and σb2 at λb1=0.7, λb2=0.35 accordingly

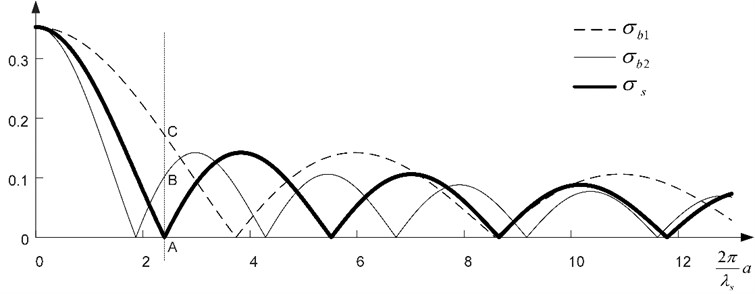
As it is mentioned in Eq. (4), the area of the secret information in time-averaged image becomes uniformly grey if only the amplitude of oscillations $a$ is equal to $a={\frac{{\lambda }_s}{2\pi }r}_i$, $i=\mathrm{1,2},\dots$. It is clear that standard deviation of uniformly grey area is equal to 0, thus ${\sigma }_s=$0 if only the amplitude of oscillations is equal to ${\frac{{\lambda }_s}{2\pi }r}_1$. Therefore, the contrast between the secret and the background depends on the value of ${\sigma }_b$ only (note that distance AC in Fig. 2 is equal to ${|\sigma }_{b1}-{\sigma }_s|={\sigma }_{b1}$ and distance AB is equal to ${|\sigma }_{b2}-{\sigma }_s|={\sigma }_{b2}$ at the point where $\frac{2\pi }{{\lambda }_s}a=r_1$).

Let us assume that the contrast of the leaked secret in time-averaged cover image is sufficient, if standard deviation ${\sigma }_b$ is equal or exceeds threshold $\delta$:

whereas amplitude of oscillation is preset to $a=\frac{\lambda }{2\pi }{r}_1$, Eq. (7) yields:

The inequality Eq. (8) is visualized in Fig. 3 when ${\lambda }_s$ is fixed. Striped intervals on the graph show the intervals of ${\lambda }_b$ for which the inequality $\left|J_0\left(\frac{{\lambda }_s}{{\lambda }_b}{r}_1\right)\right|/\sqrt{8}\ge \delta$ holds true. Zeroes of the function $J_0\left(\frac{{\lambda }_s}{{\lambda }_b}{r}_1\right)$ are located at ${\lambda }_b={\lambda }_s\frac{r_1}{r_i}$, $i=\mathrm{1,2},\dots .$

Function $J_0\left(\frac{{\lambda }_s}{{\lambda }_b}{r}_1\right)$ can be approximated by its tangent in the root surrounding if the threshold $\delta$ is relatively small. It is known, that $J_0^{\text{'}}\left(x\right)={-J}_1\left(x\right)$, where $J_1\left(x\right)$ is first order Bessel function of the first kind. Therefore, the slope of tangent line at point ${\lambda }_b={\lambda }_s$ is $k_1=J_0\text{'}\left(r_1\right)={\frac{r_1}{{\lambda }_s}J}_1\left(r_1\right)$.

Analogously the slope at point ${\lambda }_b={\lambda }_s\frac{r_1}{r_2}$ reads $k_2=J_0\text{'}\left(r_2\right)={\frac{r_2^2}{r_1{\lambda }_s}J}_1\left(r_2\right)$. Now ${\mathrm{\Delta }}_i$, $i=\mathrm{1,2},\dots$ (Fig. 3) can be approximated as ${\mathrm{\Delta }}_i=\frac{\delta }{k_i}.$

Fig. 3Visualization of the inequality J0λsλbr1/8≥δ in the interval 0.2λs;1.5λs. Thick solid line represents the variation of J0λsλbr1/8; tangents at points λs and λsr1r2 are displayed by thin lines

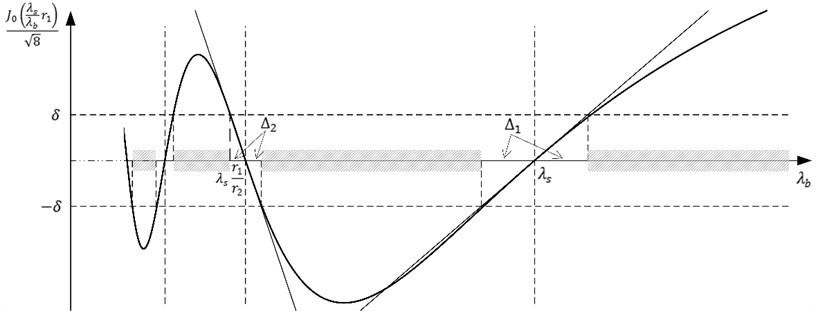
Finally, the approximate solution of inequality in Eq. (8) if $\delta$ is relatively small can be written as:

Computational solutions of inequality in Eq. (8) are presented in Fig. 4: all ${\lambda }_b$ located in the uniformly grey and striped grey areas fit the inequality at the predefined values of $\delta$. Black lines show the boundaries of the approximate solution in Eq. (9).

Fig. 4Solutions of the inequality J0λsλbr1/8≥δ: grey color indicates areas where J0λsλbr1/8≥δ, striped grey areas – where J0λsλbr1/8≤-δ, black lines corresponds to the boundaries of the approximate solution in Eq. (9)

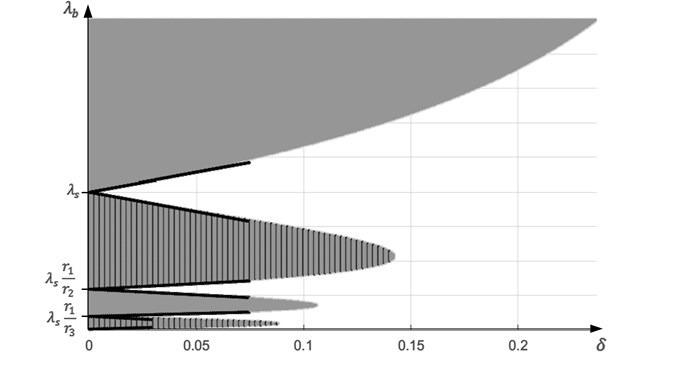
If we want to obtain sufficient predetermined contrast between secret and background areas (${\sigma }_b=\delta$), it would be optimal to choose such values ${\lambda }_b$ that lye on the contours of the grey and striped grey areas in Fig. 3, or, if $\delta$ is small, the approximate optimal solution is:

Note, that the difference between values ${\lambda }_s$ and ${\lambda }_b$ still should be small enough in order to ensure the safety of the visual encoding scheme.

4. Conclusions

The secure encryption and successful decryption of the secret information in dynamic visual cryptography is generally based on the correct determination of the moiré grating parameters. This paper proposes the graphical scheme as well as the approximate solutions for the preselection of the near optimal pitches of moiré grating. The pitch standing for the secret information should ensure uniformly grey secret area in the time-averaged image (standard deviation of the area is equal to zero). The pitch of the background should guarantee high enough standard deviation in the time-averaged background. Such near-optimal pair of the pitches of moiré grating provides sufficient contrast of the decoded image and ensures that no secret information is visible in the static cover image.