Abstract
We study stress paths that are obtained under proportional deformations within the rate-independent hypoplasticity theory of Kolymbas type describing granular materials like soil and broken rock. For a particular simplified hypoplastic constitutive model by Bauer, a closed-form solution of the corresponding system of non-linear ordinary differential equations is available. Since only negative principal stresses are relevant for the granular body, the feasibility of the solution consistent with physics is investigated in dependence of the direction of a proportional strain path and constitutive parameters of the model.
Highlights
- Explicit solution to the hypoplastic model of Kolymbas type in simplified version by Bauer is obtained in a closed form
- Mathematically confirmed that, under monotonic deformation, stress paths tend asymptotically towards an independent stress state
- Location of principal stresses in the negative octant is proved, which is a physical requirement for cohesionless granular materials
- Admissible range of the values of constitutive constants to model the asymptotic behavior of stress paths is represented in a diagram
- This study provides reasonable analytic solutions for numerical validation tests
1. Introduction
The constitutive stress-strain relation for hypoplastic granular materials like cohesionless soil or broken rock is under our consideration. The respective constitutive law is of the rate type, incrementally non-linear, and it is based on the concept of hypoplasticity proposed in 90th by Kolymbas [1]. Compared to incrementally linear constitutive equations, e.g. for hyperelastic and hypoelastic material laws, the hypoplastic constitutive equations are not differentiable at zero strain rate. This results in different stiffnesses for loading and unloading which is typical for inelastic materials. In contrast to the classical elastoplastic concept, the strain in the theory of hypoplasticity is not decomposed into the elastic and plastic parts. For modelling of soil behavior with hypoplasticity we cite [2-4], and refer to [5, 6] for other mathematical approaches. The underlying relations lie within the general context of implicit constitutive theories, see e.g. introduction in [7] and references therein.
An intrinsic property of granular materials observed in experiments is that under monotonic deformation the corresponding stress paths tends asymptotically towards a stress state, which is independent on the initial stress state [2-4]. As asymptotic states are well defined, such states are preferably qualified for the calibration of the constitutive constants. The present paper presents a novel investigation of the possible range of the values of constitutive constants to model the asymptotic behavior of stress paths under proportional deformation in hypoplasticity. Particular attention is paid on the restriction of stress states located in the negative octant of the space of principal stresses which is, from the physical point of view, a general requirement for cohesionless granular materials. Such behavior of granular materials is of practical importance for constitutive modelling not only in hypoplasticity, but, more widely, in soil mechanics and geotechnical engineering. This study also provides reasonable analytical solutions for numerical validation tests, thus it has a significant impact on efficient numerical simulations.
In the present paper, a simplified version of the hypoplastic model described in Bauer [8] and Gudehus [9] is considered. For the sake of simplicity, the pressure and density dependent properties of granular materials are omitted so that only two constitutive parameters remain in the model. Further relying on proportional strain paths, the rate model is reduced to a system of non-linear ordinary differential equations (ODE). As the result of these simplifications, the stress path is determined by the direction of a proportional strain path, by the initial stress state and the two constitutive parameters involved in the hypoplastic equation.
The main challenge in developing proper mathematical tools is the strongly non-linear character of the underlying ODE system. Following the rate-independent technique developed in [10], for the simplified hypoplastic model, the asymptotic behavior was proved in our previous work [11]. Then in [12] we constructed the solution of the corresponding non-linear problem in a closed form, and extended it to a modified model in [13]. The exact solution allows us to describe analytically the evolution of stress paths for various loading scenarios obtained from monotonic compression, extension, and isochoric deformations.
Since only negative principal stresses are relevant for the granular body, it is important to discuss the feasibility of a solution which is consistent with physics. In the present contribution, on the basis of a closed-form solution we identify the domain of the constitutive parameters which guarantee that the corresponding stress path starting from feasible initial stress state remains feasible under proportional deformation paths.
2. Theory
In the space of symmetric 3-by-3 tensors of second order, which are undersigned with the upper tilde, we assume that the strain tensor and the corresponding constant quantity are given by proportional paths with respect to the monotonic increasing parameter as:
The tensor is normalized by the Frobenius norm and determines a prescribed constant direction of the proportional strain path. Based on Eq. (1), the rate-independent hypoplastic relations take the form of the following non-linear ODE system with respect to the unknown symmetric Cauchy stress tensor (see [11-13] for more modelling issues):
where stands for the scalar product of tensors, and the trace implies . The dimensionless tensor is spanned by and the identity tensor as follows:
The initial condition for Eq. (2) prescribes the initial stress tensor at :
From a physical point of view, the constitutive parameter in Eq. (2) scales the amount of and the second constitutive parameter characterizes the shape of the conical limit stress surface or so-called critical stress state surface in the principal stress space [8]. By this we have assumed deformations for which the objective time derivative coincides with the material time derivative, that holds for example for coaxial deformations.
A closed-form solution to the initial value problem given by Eqs. (2-4) was found in [12-13]:
where the values , , and are defined as follows:
Since only negative principal stresses , , are relevant for the underlying physical model of granular solids, it is important to discuss their feasibility.
2.1. Computational simulation
We present a computational example of coaxial deformation according to Eqs. (5-6). Set the parameter values:
such that and . Eq. (3) determines the tensor:
with . For the value of the initial stress tensor we choose . Then the parameters from Eq. (6) are calculated as:
As the corresponding material behavior is coaxial, the stress tensor has zero elements outside the diagonal, thus , and from Eq. (5) we get:
In Fig. 1 (a) we show for coaxial deformation the diagonal of as a direction vector of the proportional deformation prescribed in the coordinate system , , . Then the proportional strain path from Eq. (1) forms a half-line along for . The dashed line here is the isotropic axis. Intersection of a perpendicular plane with the negative octant constitutes an equilateral triangle drawn for visualization reason. In Fig. 1(b) the diagonals of tensors , , are depicted in the coordinates , , . Starting as at marked by the cross, the stress path (marked by a solid curve) approaches the half-line along a vector as . The asymptotic behavior was investigated in our previous works [11-13]. In the present context, it is worth noting that , and for all lie in the negative octant in Fig. 1(b) (although not in Fig. 1(a)), thus implying a feasible solution consistent with physics.
Fig. 1Computational simulation example: a) orientation of the proportional strain path prescribed and b) asymptotic behavior of the corresponding stress path
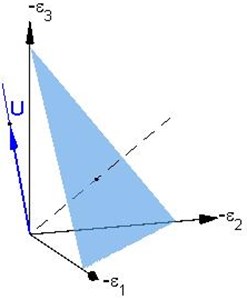
a) Principal strain space
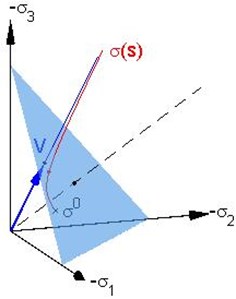
b) Principal stress space
3. Feasibility conditions
According to the analytic solution from Eqs. (5-6), the stress path lies in the hyperplane spanned by and . Therefore, we define a cone of feasible directions depending on and such that:
where , , are eigenvalues of . That means that is the set of all directions that lie in the negative octant and that can be reached by Eq. (3). On the other hand, we define a cone of feasible stresses such that:
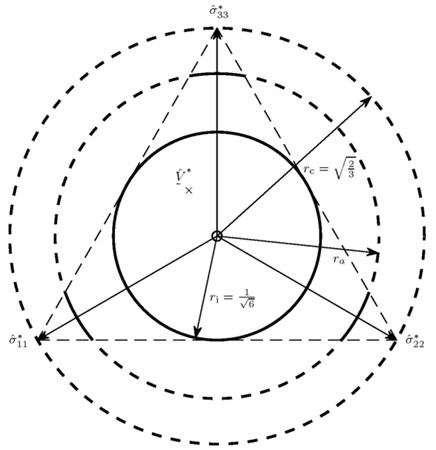
where , , imply the principal stresses corresponding to . We draw both and in the same Fig. 2.
In the space of principal stresses the apex of the cone lies in the origin of the principal stress axes. In the stress space the so-called deviator plane is defined as the plane for –1, and the intersection of this plane with the negative octant constitutes an equilateral triangle with the side length of as shown in Fig. 2. In the figure we use marks for the axes . Furthermore, the intersection of the deviator plane with a circular cone with apex at the origin and main axis perpendicular to the deviator plane is represented by a disc of some radius . We can draw the circumcircle with radius and the incircle with radius of this triangle. The intersection of the above triangle with a disc of radius forms the cone . The value of depends on , see [14].
Note that for feasible from Eq. (7). Therefore, if in Eq. (6), then (recalling that ), so that the factors in front of and in Eq. (5) are positive. Choosing both and the initial stress state thus guarantees that the whole stress path is contained in for all .
We now investigate necessary and sufficient conditions on and to ensure that .
Fig. 2Representation of the intersection of the limit cones with the deviator plane in the principal stress space
3.1. Lower boundary of admissible parameters
Let be as in (3) and let us assume that . Then is the axial projection of onto the deviator plane, which for instance is marked with the cross in Fig. 2. Let denote its distance from the center of the triangle. By definition of we have:
The norm in the numerator can be evaluated using the condition (which implies that ) as follows:
Finally, we define to be the minimal value such that:
for all such that . The maximum in Eq. (9) over all admissible values of is reached for , that is:
Hence, a sufficient condition for to belong to independently of the strain rate direction is given by Eq. (10) for , that is:
For , the condition is fulfilled only for certain values of , namely those for which according to Eq. (9). Taking into account the constraint , we rewrite Eq. (9) as:
The critical value of is such that:
that is If , then Eq. (11) holds for all . Otherwise, for , only the values:
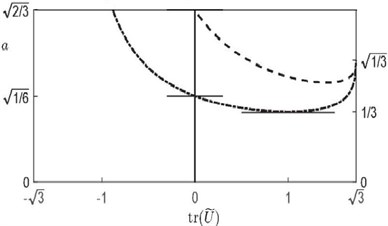
are admissible, and the lower boundary of the admissible parameter domain is represented by the dot-dashed curve in Fig. 3.
3.2. Upper boundary of admissible parameters
The question is more delicate if the pair lies above the dot-dashed line in Fig. 3. As long as in Eq. (10) is between and as in Fig. 2, the circle of radius intersects the triangle in the negative octant. In other words, some points at the distance from the center of the triangle fall out of . The points with do not belong to at all. The case of can be treated similarly as above. We replace Eq. (9) with:
still under the constraint , and obtain:
The critical value of is such that:
that is If , then Eq. (14) is never satisfied for any . Otherwise, for , only the values:
exclude the possible existence of points at the distance belonging to . The dashed curve in Fig. 3 represents the upper boundary of this parameter domain.
Fig. 3Visualization of the domain of parameters with feasibility conditions
4. Conclusions
The simplified hypoplastic constitutive Eq. (2) considered in this paper is incrementally non-linear and includes only two constitutive parameters: a stiffness parameter and a parameter related to the critical friction angle of a cohesionless granular material, which is defined for the axisymmetric triaxial compression in the limit state. Although the influence of the direction of the stress deviator on the critical stress state is neglected, i.e. the constitutive parameter is assumed to be constant, it does not mean a restriction of the general results drawn. A relevant relation between the value of parameter for the direction of the stress deviator of triaxial compression and the one for another direction can be obtained by interpolation.
For future work, we propose to study the simplified hypoplastic model under cyclic loading, when the granular solid exhibits the so-called ratchetting effects of fading and shifting hysteresis loops.
References
-
Kolymbas D. An outline of hypoplasticity. Archive of Applied Mechanics, Vol. 61, 1991, p. 143-151.
-
Gudehus G. Physical Soil Mechanics. Springer, Berlin, Heidelberg, 2011.
-
Kolymbas D., Medicus G. Genealogy of hypoplasticity and barodesy. International Journal for Numerical and Analytical Methods in Geomechanics, Vol. 40, 2016, p. 2532-2550.
-
Mašín D. Modelling of Soil Behaviour with Hypoplasticity. Springer Nature, Switzerland, 2019.
-
Annin B. D., Kovtunenko V. A., Sadovskii V. M. Variational and hemivariational inequalities in mechanics of elastoplastic, granular media, and quasibrittle cracks. Analysis, Modelling, Optimization and Numerical Techniques. Springer Proceedings in Mathematics and Statistics, Vol. 121, 2015, p. 49-56.
-
Khludnev A. M., Kovtunenko V. A. Analysis of Cracks in Solids. WIT-Press, Southampton, Boston, 2000.
-
Itou H., Kovtunenko V. A., Rajagopal K. R. Well-posedness of the problem of non-penetrating cracks in elastic bodies whose material moduli depend on the mean normal stress. International Journal of Engineering Science, Vol. 136, 2019, p. 17-25.
-
Bauer E. Calibration of a comprehensive hypoplastic model for granular materials. Soils and Foundations, Vol. 36, 1996, p. 13-26.
-
Gudehus G. A comprehensive constitutive equation for granular materials. Soils and Foundations, Vol. 36, 1996, p. 1-12.
-
Brokate M., Krejčí P. Wellposedness of kinematic hardening models in elastoplasticity. RAIRO Modélisation Mathématique et Analyse Numérique, Vol. 32, 1998, p. 177-209.
-
Kovtunenko V. A., Krejčí P., Bauer E., Siváková L., Zubkova A. V. On Lyapunov stability in hypoplasticity. Proceedings of Equadiff Conference, Bratislava, 2017, p. 107-116.
-
Bauer E., Kovtunenko V. A., Krejčí P., Krenn N., Siváková L., Zubkova A. V. On proportional deformation paths in hypoplasticity. Acta Mechanica, 2020, https://doi.org/10.1007/s00707-019-02597-3.
-
Bauer E., Kovtunenko V. A., Krejčí P., Krenn N., Siváková L., Zubkova A. V. Modified model for proportional loading and unloading hypoplastic materials. Extended Abstracts Spring 2018. Trends in Mathematics, Vol. 11, 2019, p. 201-210.
-
Bauer E. Conditions for embedding Casagrande’s critical state into hypoplasticity. Mechanics of Cohesive-Frictional Materials, Vol. 5, 2000, p. 125-148.
About this article
This work was supported by the OeAD Scientific and Technological Cooperation (WTZ CZ 01/2016 and 18/2020) financed by the Austrian Federal Ministry of Science, Research and Economy (BMWFW) and by the Czech Ministry of Education, Youth and Sports (MŠMT).
Further support by the Russian Foundation for Basic Research (RFBR) and JSPS research project 19-51-50004 (V.A.K.) and by the European Regional Development Fund, Project No. CZ.02.1.01/0.0/0.0/16_019/0000778 (P.K.) is gratefully acknowledged.
