Design and accuracy test of equatorial moment of inertia test equipment for projectile and rocket

1. Introduction

When the projectile bypasses the center of mass and rotates in a plane perpendicular to the rotation axis, the measured moment of inertia is the equatorial moment of inertia. The commonly used methods to measure the moment of inertia mainly include the compound pendulum method [1], the torsion pendulum method [2], and the three-wire pendulum method [3]. Che Ying and others designed and manufactured the instrument for measuring the moment of inertia of a small projectile [4] by using the double suspension wire torsion pendulum mechanism, which realizes the precise measurement of the moment of inertia of a small projectile, but the instrument is not suitable for the measurement of the moment of inertia of large projectile and arrow. Li Huipeng and others developed the missile moment of inertia test system based on the torsion pendulum method. Due to the use of an air-floating turntable mechanism, the measurement accuracy is less than 0.1% [5], but the manufacturing cost is high. Due to its advantages of good safety and high measurement accuracy, the torsion pendulum method has been more applied to the measurement of inertial parameters of high-tech equipment such as satellites [6] and missiles [7]. In this paper, the torsion pendulum method is used to design the polar moment of inertia test equipment for projectile and arrow, and the accuracy of the equipment is analyzed, which can meet the needs of the equatorial moment of inertia test of projectile and arrow.

2. Principle of equatorial moment of inertia measurement

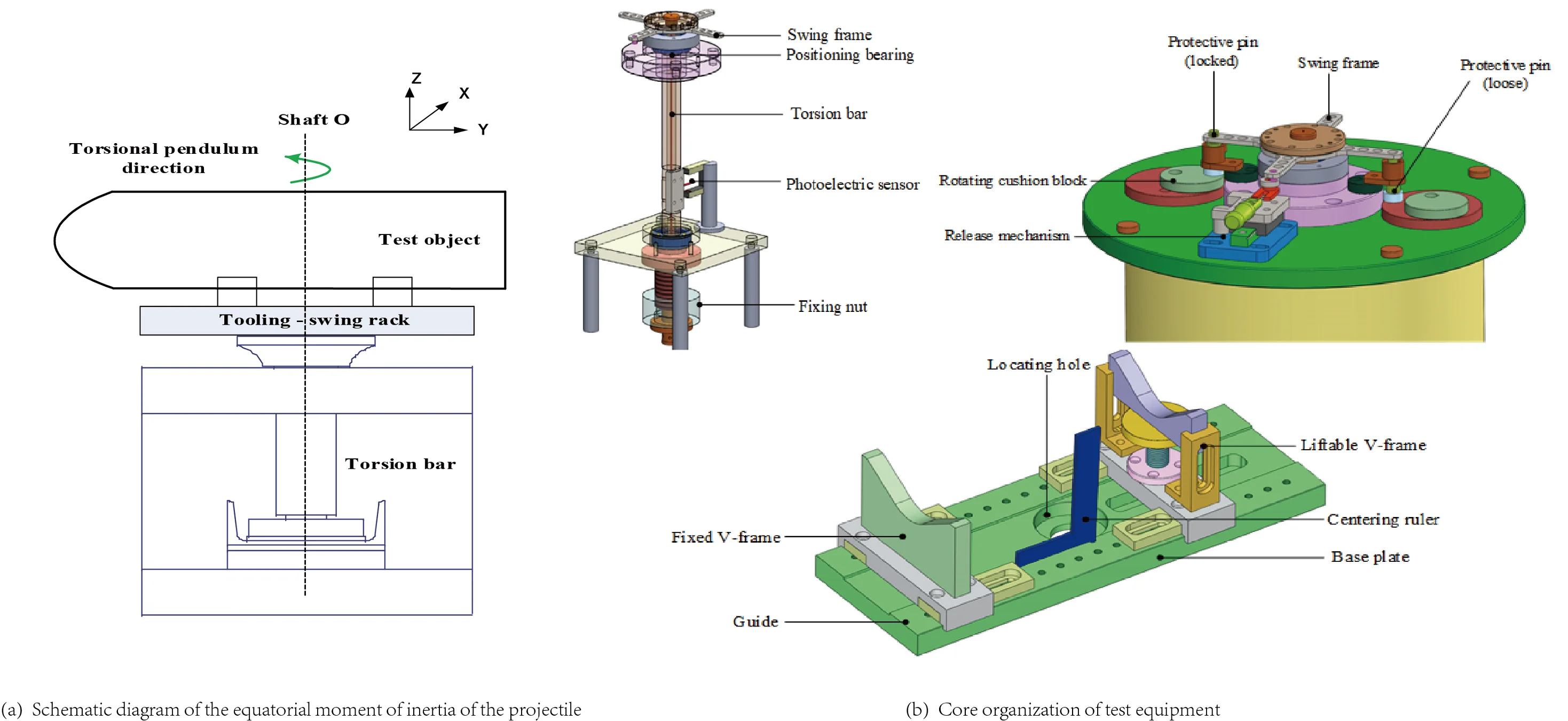
For projectiles with a large aspect ratio [8], the torsion pendulum method is mostly used to measure the equatorial moment of inertia. This method has the advantages of high accuracy and high test efficiency [9-11]. The principle of measuring the equatorial moment of inertia of large mass projectile and arrow by torsion pendulum method is shown in Fig. 1.

According to the law of rotation, the motion equation of the system is shown in Eq. (1):

Eq. (2) is a variation of Eq. (1):

where, $2n=c/J$ and $p^2=k/J$ are damping coefficient and undamped frequency respectively. When $n<p$, the solution of the differential equation can be expressed as Eq. (3):

where: $\overline{p}=\sqrt{p^2-n^2}$, $\overline{T}=2\pi /\overline{p}=2\pi /\sqrt{p^2-n^2}$. Then the moment of inertia $J$ of the projectile is calculated by measuring the damping swing period $\overline{T}$.

Fig. 1Schematic diagram of the equatorial moment of inertia of the projectile

3. Composition of measuring equipment

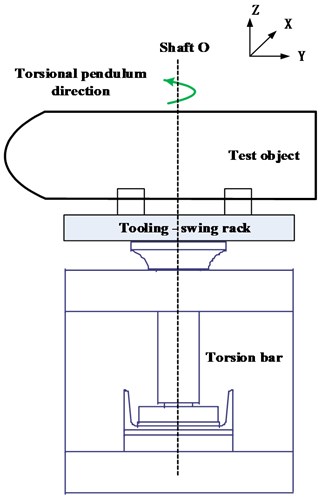
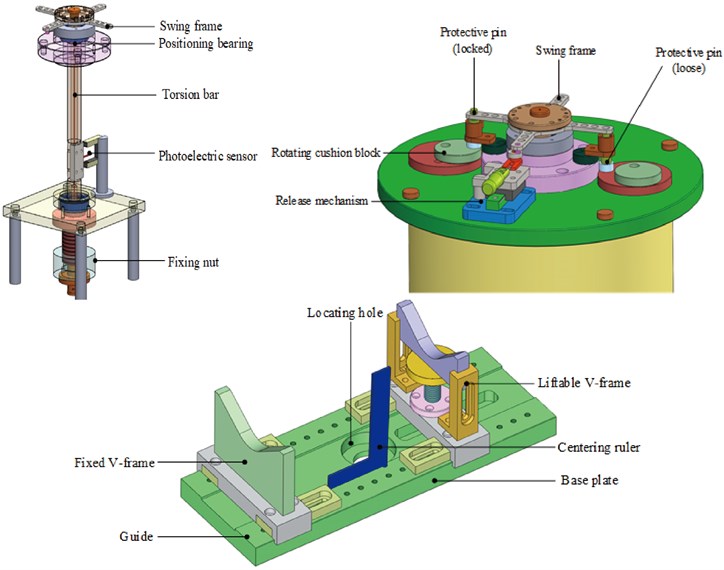
The equatorial moment of inertia measuring platform for projectile and rocket is composed of a base, torsion pendulum system, pendulum system, and test tooling. The core mechanism of the test equipment is shown in Fig. 2.

When measuring the equatorial moment of inertia, place the projectile and arrow horizontally on the tooling. After the system is stable, apply an external force and push the release handle reversely. The swing frame will twist freely. After swinging for a certain number of cycles, the computer will get the cycle value. Using the mathematical calculation model of an equatorial moment of inertia, the data are analyzed and processed by a computer, and then the equatorial moment of inertia to be measured is obtained.

4. Error analysis

4.1. Measurement error caused by damping

This measuring device belongs to an underdamped system. $n<1$, $\overline{p}=p\sqrt{1-(n^2/p^2)}$, $\overline{T}=2\pi /\overline{p}=T/\sqrt{1-(n^2/p^2)}$. It can be seen that the existence of damping causes the vibration period of the system to become larger. When $n^2/p^2=$ 0.05, the actual vibration period can be expressed as Eq. (4):

4

$\overline{T}=T\frac{1}{\sqrt{1-(n^2/p^2)}}=1.001T.$

Therefore, the relative error of equatorial moment of inertia caused by damping can be expressed as Eq. (5):

5

$\mathrm{\Delta }=\frac{\overline{T}-T}{T}\times 100\%=0.2\%.$

Fig. 2Core organization of test equipment

5. Conclusions

In this paper, the torsional pendulum method is used to measure the equatorial moment of inertia of large missiles and arrows, and the measurement principle is deeply analyzed. Based on the torsional pendulum method, an equatorial moment of inertia test equipment is designed. The equipment has the advantages of simple design and manufacture, safe and efficient structure, and can effectively measure the equatorial moment of inertia of large missiles and arrows. The causes of measurement error are analyzed, and the measurement accuracy of the equipment is verified by experiments. The maximum relative error is less than 1 %, and the relative uncertainty is 1.3926 %, which meets the requirements of expected technical indicators.