On the decisional problem based on matrix power function defined over non-commutative group

1. Introduction

A novel idea presented by W. Diffie and M. Hellman in [1] of using a pair of keys to agree on a shared secret gave birth to the branch of public-key cryptography. Since then, much research has been performed in this field and widely known cryptosystems such as RSA and many others were proposed. However, these cryptosystems mostly relied on the security of the discrete logarithm problem (DLP) defined in some multiplicative group (a version of DLP for additive groups e.g. elliptic curves can also be defined) or integer factorization problem [2]. While these problems do provide a decent challenge, due to the findings published by P. Shorr in [3] these problems could be solved by quantum computers.

For some time, quantum computers were viewed as a mostly theoretical threat. However, due to the rapid development of quantum technologies, by the mid-2010s quantum cryptanalysis could no longer be viewed as purely theoretic. In 2016 the National Institute of Standards and Technology (NIST) announced a call for post-quantum algorithms for standardization [4]. As of now the finalists of round 3 have been announced [5]. Furthermore, the development of quantum-safe cryptographic schemes continues due to the increasing practical demand of such algorithms in the near future.

The proposed cryptographic schemes rely on hard problems e.g. defined in lattices or using multivariate quadratic equations. Alternatively error correction codes, hash-based cryptography or elliptic curves isogenies could be used to construct quantum-safe algorithms [6,7]. The security of such algorithms relies on NP-hard computational problems, i.e. they are in the hardest class of problems which cannot be solved by a deterministic Turing machine in polynomial time. Moreover, decisional versions of some of these problems are known to be NP-complete, e.g. closest vector problem used in lattice-based cryptography [8]. It is widely believed that such problems can withstand quantum cryptanalysis.

In this paper, we consider one of such problems which is fundamental for the security of the cryptographic protocols presented in [9] and [10]. The objective of this problem is to recover the secret key of the legitimate user based on his public key [9]. Our goal is to show that the produced key is statistically indistinguishable from a truly random matrix if the public parameters of the protocol are appropriately chosen. We think that our results pose an interest from the practical implementation point of view, since the choice of the security parameters influences the memory requirements to store the private and public data and hence can be fundamental to determining if our proposal can be implemented in memory-restricted devices.

The rest of this paper is organized as follows: in Section 2 we revise the mathematical background of our research; in Section 3 we define the considered problem in the form of the security game and present the main results of this paper. As usual, conclusions are presented at the end of the paper.

2. Mathematical background

Our approach is related to multivariate cryptography. Specifically, we focus on a certain mapping called the matrix power function (MPF) first introduced in [11]. The idea of this mapping is somewhat similar to the classical matrix multiplication. However, since MPF is defined for matrices with entries chosen from multiplicative (semi)group $\mathbb{S}$, we use multiplication as the operation in $\mathbb{S}$ and exponentiation as the scalar multiplication. Hence, we obtain the following expressions defining the one-sided MPFs [11]:

The matrix $\mathbf{W}$ in Eq. (1) and Eq. (2) is called the base matrix with its entries chosen from the multiplicative (semi)group $\mathbb{S}$. We refer to $\mathbb{S}$ as the platform (semi)group. The matrices $\mathbf{X}$ and $\mathbf{Y}$ in Eq. (1) and Eq. (2) respectively are referred to as power matrices. Their entries are chosen from a ring of scalars ${\mathbb{Z}}_{ord\left(\mathbb{S}\right)}$, where $ord\left(\mathbb{S}\right)$ denotes the multiplicative order of $\mathbb{S}$, i.e. the smallest natural number satisfying the relation $w^{ord\left(\mathbb{S}\right)}=e$ for any $w\in \mathbb{S}$, and $e$ is the identity of $\mathbb{S}$.

In our early research related to MPF we considered various commuting platform groups [12–14]. It was shown in [12] that is this case MPF is associative, i.e. the following identity holds:

Hence, we obtain the definition of the two-sided MPF. Unfortunately, our early proposals presented in [12] and [14] were attacked in [15] using tools of linear algebra together with discrete logarithm mapping. Though we fixed the flaw in our paper [16], and investigated this enhanced version in [17], partly due to the presented attack, our attention turned to non-commuting platform groups, where Eq. (3) does not hold in general, and hence the order of actions must be taken into consideration. In [9] and [18] we have shown that we can define hard decisional problems based on MPF defined over non-commuting platform groups thus demonstrating that MPF is a possible candidate for the so-called one-way function – easy to calculate, hard to invert.

In this paper, we consider a family of the so-called modular-maximal cyclic groups generally denoted by ${\mathbb{M}}_{2^t}$ and defined as follows [19-21]:

where $a$ and $b$ are two non-commuting generators of the group and e is the identity of the group. Note that the parameter t defines the size of ${\mathbb{M}}_{2^t}$, i.e. $\left|{\mathbb{M}}_{2^t}\right|=2^t$, and hence we refer to it as the group-defining parameter. All the elements of ${\mathbb{M}}_{2^t}$ can be represented in two ways: either $a^{\alpha }{b}^{\beta }$ or $b^{\beta }{a}^{\alpha }$, where $\alpha \in {\mathbb{Z}}_{2^{t-1}}$ and $\beta \in {\mathbb{Z}}_2$. Since both these representations are equivalent, in this paper, we use the representation $a^{\alpha }{b}^{\beta }$ for the elements of ${\mathbb{M}}_{2^t}$.

Basic operations in this group are presented below [9].

Multiplication of two elements:

Exponentiation to the power $k$:

An important corollary of these expressions is the fact that there are two cyclic subgroups of ${\mathbb{M}}_{2^t}$ of size $2^{t-1}$. These subgroups are generated by elements $a$ and $ab$. We denote them by $〈a〉$ and $〈ab〉$ respectively. Their explicit presentations are given below:

It is important to note that in general elements from $〈a〉$ and $〈ab〉$ do not commute. This fact plays a major role in the application of ${\mathbb{M}}_{2^t}$ in our research. Specifically, we defined the form of the base matrix $\mathbf{W}$ as well as the forms of the secret key matrices.

Template 1. The base matrix $\mathbf{W}$ is chosen randomly to fit the following form [9]:

The main idea behind this template is to choose the entries of the columns in such a way that in each of the individual column entries are in the same cyclic subgroup either $〈a〉$ or $〈ab〉$. This way we ensure that each individual column contains commuting entries. However, we still have to make sure that the exponentiation from the right is also performed with commuting entries. To achieve this goal, we define the following templates for power matrices [9]:

Template 2. The left power matrix $\mathbf{X}$ is chosen at random to satisfy the following condition:

Template 3. The right power matrix $\mathbf{Y}$ is chosen at random to satisfy the following condition:

Previously in [9] we proposed a key exchange protocol where we used ${\mathbb{M}}_{2^t}$ as a platform group for the MPF with similar templates for matrices. Also, using the ideas presented in that paper we proposed a sigma identification protocol in [10]. Here we focus on these ideas presented in a more general way, i.e. we consider the MPF with additional constraints given by the Templates 1, 2 and 3 defined above to keep the results obtained here applicable for future research in this area.

3. Decisional problem based on MPF

In this section we consider the following security game aimed at distinguishing an MPF value from a truly random matrix:

Security Game. Let $\mathbf{W}$ be a matrix satisfying Template 1. For a given adversary $\mathcal{A}$ and its challenger $\mathcal{C}$ we define the following game:

1) $\mathcal{C}$ chooses at random two matrices $\mathbf{X}$ and $\mathbf{Y}$ satisfying Templates 2 and 3 respectively and computes ${\mathbf{K}}_0={\left({}_{\mathit{}}{}^{\mathbf{X}}\mathbf{W}\right)}^{\mathbf{Y}}$.

2) $\mathcal{C}$ generates a random matrix ${\mathbf{K}}_1$ with entries ${\left(k_1\right)}_{ij}\in {\mathbb{Z}}_{2^{t-1}}$.

3) $\mathcal{C}$ gives the pair $\left(\mathbf{W},{\mathbf{K}}_{\beta }\right)$, where $\beta \in \left\{\mathrm{0,1}\right\}$ to $\mathcal{A}$.

4) $\mathcal{A}$ outputs $\widehat{\beta }$.

The adversary $\mathcal{A}$ wins the game if $\widehat{\beta }=\beta$.

To put it simpler, the aim of the game is to answer YES/NO to the following question: is there a pair of matrices $\left(\mathbf{X},\mathbf{Y}\right)$ satisfying Templates 2 and 3 respectively, such that ${\mathbf{K}}_{\beta }={\left({}_{\mathit{}}{}^{\mathbf{X}}\mathbf{W}\right)}^{\mathbf{Y}}$. Hence, we obtain a decisional problem based on MPF defined over a non-commutative platform group. Here we refer to this problem as MPF decisional problem.

Previously in [9] we used Schaefer’s dichotomy theorem to show that a special case of this problem when matrices $\mathbf{X}$ and $\mathbf{Y}$ are generated as polynomials of pre-fixed matrices $\mathbf{L}$ and $\mathbf{R}$ with coefficients from ${\mathbb{Z}}_{2^{t-1}}$ is NP-complete. However, we did not explore the dependence of the complexity of this problem on the order of the matrices or the size of the platform group ${\mathbb{M}}_{2^t}$. Here we focus on these dependencies, i.e. we are interested in determining how difficult it is to solve the considered decisional problem for distinct values of the group size-defining parameter $t$ and the matrix order $m$.

Our results are based on the statistical analysis of the distribution of the entries of the MPF value matrix ${\mathbf{K}}_0$. Our goal is to show that the entries of ${\mathbf{K}}_0$ are distributed uniformly in ${\mathbb{Z}}_{2^{t-1}}$ as a truly random matrix ${\mathbf{K}}_1$ has uniformly distributed entries.

The statistical analysis was performed as follows:

1) We generate a matrix $\mathbf{W}$ that satisfies Template 1.

2) We select a natural number k that defines the total number of iterations executed.

3) Within the $l$-th iteration, where $1\le l\le k$, a new pair of matrices $\left({\mathbf{X}}_l,{\mathbf{Y}}_l\right)$ is generated such that the matrix ${\mathbf{X}}_l$ satisfies Template 2 and the matrix ${\mathbf{Y}}_l$ satisfies Template 3. For each pair we calculate the matrix exponent ${\mathbf{V}}_l={\left({}_{\mathit{}}{}^{{\mathbf{X}}_l}\mathbf{W}\right)}^{{\mathbf{Y}}_l}$.

4) We store the frequencies of powers of the generator $a$ two different ways: an array $\mathbf{q}$ stores the overall frequencies of powers, and a tensor $\mathbf{Q}$ keeps track of frequencies in each individual position in the matrix exponent, i.e. we obtain $m^2$ separate samples, where $m$ is the size of the matrices. Denote by $f\left(z,{\mathbf{V}}_l\right)$ the frequency of the element $a^z$ in the matrix exponent ${\mathbf{V}}_l$ and denote by $f_{ij}(z,{\mathbf{V}}_l)$ the frequency of the element $a^z$ in the $\left(i,j\right)$-th position of matrix exponent ${\mathbf{V}}_l$. Then we have:

5) After all $k$ iterations have been executed, we perform Pierson chi-squared test for uniform distribution for $\mathbf{q}$ and each sample ${\mathbf{q}}_{ij}\in \mathbf{Q}$ separately at a 0.05 significance level and calculate $p$-value for all of the obtained values of the chi-squared statistics.

If the null hypothesis is rejected for the sample $\mathbf{q}$, then there may exist patterns in the structure of the key matrix ${\mathbf{K}}_0$ distinguishing it from a truly random matrix, i.e. some values of ${\mathbf{K}}_0$ might be more likely than others. Hence an adversary has a non-negligible chance of winning the security game defined above. Moreover, if the null hypothesis is rejected for multiple samples ${\mathbf{q}}_{ij}$ of the tensor $\mathbf{Q}$ then there is a potential threat of pattens for some individual positions and the adversary may use this partial information leak to win the considered security game with non-negligible probability, if these patterns are stable under repeats of the experiment.

Let us consider an example of the performed experiment consisting of $k=$1000 iterations. Assume the parameter values $t=\text{4}$ and $m=\text{8}$. The following base matrix $\mathbf{W}$ was generated:

Note that for this choice of $\mathbf{W}$ we have $c=5$ in Eq. (11).

Since there are a total of $1000$ pairs $({\mathbf{X}}_i,{\mathbf{Y}}_i)$ generated and matrix exponents ${\mathbf{V}}_i$ calculated, here we present only the matrices obtained during the first iteration as the example:

The histogram after 1000 iterations is presented below. Also, for comparison we have generated 1000 random matrices with entries uniformly chosen from ${\mathbb{Z}}_8$.

Due to the low p-value of the obtained results the null hypothesis is rejected in case of Fig. 1(a) and hence the tensor $\mathbf{Q}$ was not considered. We could explain this result by inspecting the elements of the given $\mathbf{W}$: since in the first and last columns even-degree powers must dominate due to Template 1 and we only have 8 columns in total, the impact of even powers is crucial when exponentiating to left and right power matrices in Eq. (1) and Eq. (2) respectively. Hence, we see that the even powers of the generator $a$ are more likely in this case.

After performing a couple of extra experiments with the same parameters, the $p$-value did not increase, so we assume that repeating the experiment does not significantly change the $p$-value. Hence, relying on the obtained results we see that the MPF decisional problem is solvable for this case. In other words, due to the observed pattern of the even powers being more frequent, we see a significant difference between the MPF value ${\mathbf{K}}_0\mathbf{}$and a truly random matrix ${\mathbf{K}}_1$ as presented in Fig. 1. Hence, the matrix order is too small to obtain a complex MPF decisional problem.

On the other hand, based on the presented results we make a conjecture that the observed parity effect becomes less noticeable or even disappears as the size of the matrix increases, since the matrix $\mathbf{W}$ contains more free columns and the impact of the three specific columns reduces.

Fig. 1Comparison of the results of the experiment to truly random data for security parameters t=4 and m=8

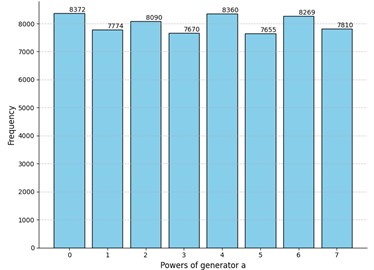
a) Histogram for the experiment data: $p$-value for sample $\mathbf{q}$: 3.5⋅10^-15

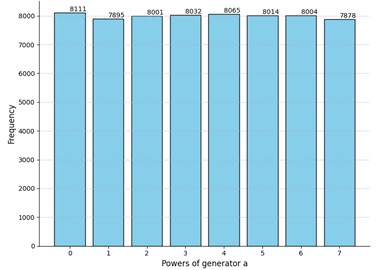
b) Histogram for truly random matrices: $p$-value for sample $\mathbf{q}$: 0.60

Let us now present our findings for the parameter values: $t=\text{4}$ and $m=\text{12}$. The idea of the experiment stays the same and the total number of iterations is $k=$1000. We suppress the explicit presentation of the matrix $\mathbf{W}$ to shorten the paper. For better comparison we repeat the experiment three times each time changing the matrix $\mathbf{W}$. Also, we have generated 1000 truly random 12×12 matrices. The results are presented in Fig. 2.

Evidently, the $p$-values differ in all cases, but all of them are greater than the selected threshold of 0.05. Interestingly enough, the p-value of the truly random data was less than the $p$-value of the Experiment 3 and comparable to other obtained $p$-values. Moreover, we can see that even for truly random data the null hypothesis was rejected for several positions of the matrix. However, there are no recognizable patterns in the positions where the uniformness was rejected. Neither the number of such positions nor their locations in the matrices are stable. Hence the adversary cannot acquire any valuable information by studying these positions which could potentially increase the probability of winning the considered security game. Relying on these observations we claim that for these parameter values the MPF value ${\mathbf{K}}_0$ is indistinguishable from a truly random matrix ${\mathbf{K}}_1$.

Additionally, we performed experiments with other values of the security parameters. Since $p$-values for the experiments greatly vary and sometimes become lower than the considered threshold. For this reason, for each platform group ${\mathbb{M}}_{16}$, ${\mathbb{M}}_{32}$, ${\mathbb{M}}_{64}$ and ${\mathbb{M}}_{128}$ we performed the search for the smallest $m$ such that the null hypothesis could not be rejected for all the experiments. We started at 8×8 matrices and increased $m$ by 1 until all 25 experiments produced $p$-values greater than 0.05. Based on the obtained results we make a conjecture that considered security game could not be won in the average case for the following parameter values shown in Table 1.

We can see from the presented results that as the cardinality of the platform group increases, the impact of even degrees becomes more noticeable. Hence, for practical implementation of our KEP it may be reasonable to consider a balance between the cardinality of the platform group and the matrix size, since large matrices require more available memory space. For example, for the platform group ${\mathbb{M}}_{16}$ and 14×14 matrices 490 bytes of memory are needed to store matrices $\mathbf{W}$, $\mathbf{L}$, $\mathbf{R}$, $\mathbf{X}$, $\mathbf{Y}\mathbf{}$and $\mathbf{A}$, whereas for the platform group ${\mathbb{M}}_{128}$ and 16×16 matrices 1216 bytes of memory are required to store this data and the protocol is potentially less secure in the statistical sense. Also, memory is required to store a vector of coefficients. Moreover, it may be a good idea to store tables for mathematical operations in the platform group as well as powers of $\mathbf{L}$ and $\mathbf{R}$ to speed up the execution of the protocol in exchange for memory.

Fig. 2Comparison of the results of the experiment to truly random data for security parameters t= 4 and m= 12

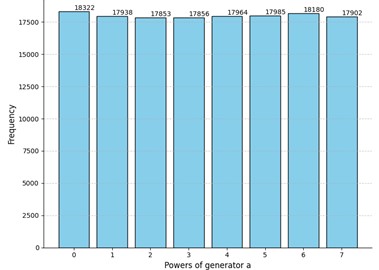
a) Experiment 1: $p$-value for sample $q$: 0.15; $H_0$ rejected for the following positions of $Q$: $\left(\mathrm{2,9}\right)$, $\left(\mathrm{4,6}\right)$, $\left(\mathrm{5,7}\right)$, $\left(\mathrm{6,6}\right)$, $\left(\mathrm{6,10}\right)$, $\left(\mathrm{6,12}\right)$, $\left(\mathrm{7,12}\right)$, $\left(\mathrm{12,5}\right)$

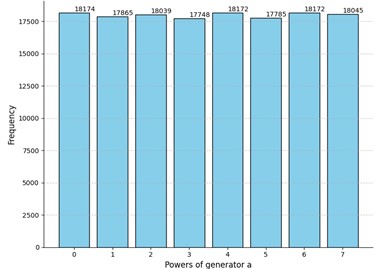
b) Experiment 2: $p$-value for sample $q$: 0.09; $H_0$ rejected for the following positions of $Q$: $\left(\mathrm{2,4}\right)$, $\left(\mathrm{3,9}\right)$, $\left(\mathrm{5,7}\right)$, $\left(\mathrm{7,9}\right)$, $\left(\mathrm{11,12}\right)$

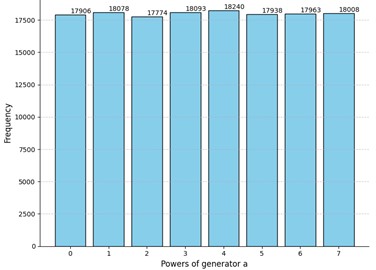
c) Experiment 3: $p$-value for sample $q$: 0.37; $H_0$ rejected for the following positions of $Q$: $\left(\mathrm{1,9}\right)$, $\left(\mathrm{4,8}\right)$, $\left(\mathrm{4,9}\right)$, $\left(\mathrm{4,10}\right)$, $\left(\mathrm{6,3}\right)$, $\left(\mathrm{8,1}\right)$, $\left(\mathrm{8,10}\right)$, $\left(\mathrm{10,9}\right)$, $\left(\mathrm{11,4}\right)$, $\left(\mathrm{11,6}\right)$, $\left(\mathrm{12,3}\right)$, $\left(\mathrm{12,10}\right)$

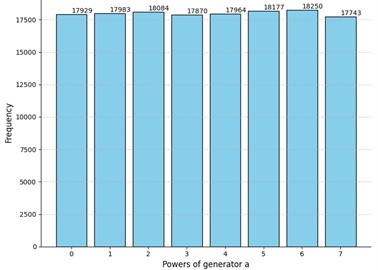
d) Truly random matrices: $p$-value for sample $q$: 0.16; $H_0$ rejected for the following positions of $Q$: $\left(\mathrm{1,11}\right)$, $\left(\mathrm{1,12}\right)$, $\left(\mathrm{2,1}\right)$, $\left(\mathrm{2,5}\right)$, $\left(\mathrm{6,11}\right)$

In conclusion we note that due to the sporadic changes of the p-value the obtained results should be viewed as recommendations based purely on statistical results. In other words, these result must be viewed as minimal recommendations for the values of public parameters. Algebraic analysis must also be taken into consideration. Such methods as the linearization technique, or the faithful matrix representation of the elements of the group ${\mathbb{M}}_{2^t}$ were not considered in this work. Should these methods provide the adversary with some useful information about private keys, we must evaluate the dangers caused by them and hopefully avoid them by appropriately increasing the values the public parameters of the system.

4. Conclusions

In this paper, we have presented the results of the statistical analysis aimed at distinguishing the public key of the legit user from a truly random matrix. We have shown that for small matrices the adversary can gain a significant advantage in winning the security game defined in Section 3 based on the distribution of the entries of the public key matrix. However, this advantage vanishes as matrices become larger. Hence, based on the presented results we could recommend considering matrices of size 14 at the very least. Additional experiments are needed to find the optimal size of matrices for large groups, i.e. when the group-defining parameter $t\ge \text{7}$.

Notably, the security of our protocol relies on a hard decisional problem. However, the latter result means that to implement our protocol in practice, we need to find the balance between the choice of public parameter values and the required memory for data storage. Furthermore, unreasonably large values of the public parameters can also negatively affect the execution time of the protocol thus making it less attractive to the designers of cryptographic software.

The obtained results will serve as a basis for our future research of other cryptographic primitives based on the MPF defined over modular-maximal cyclic groups.