Investigation of the load’s variation rate effect on the efforts and moment intensity factors values in a cylindrical shell with a longitudinal crack

1. Introduction

Cylindrical shells are important structural elements that are widely used in various industries. They are used in civil engineering, mechanical engineering, aircraft and rocketry and the chemical industry, particularly in the design of tanks, reservoirs, pipelines, machinery covers, etc., that are subject to various external loads. Such structural elements in modern engineering usually operate under the influence of a time-varying load, which requires taking into account the inertia of the shell material when studying its limit equilibrium.

At present, methods of solving problems of the stress-strain state of different kinds of shells with cracks under static loading are described in detail in numerous works [1-3]. Many fewer scientific papers deal with the limiting equilibrium of shell structures subjected to dynamic loading [4-8]. This situation is caused by the need to consider the inertia of the material in the equilibrium equations under dynamic loading, which leads to difficulty in constructing their solutions. That is why the study of the limiting equilibrium of cylindrical shells under the action of a time-varying load is an actual problem of shell theory.

This article is based on the author’s previous research. In the works of M. Nykolyshyn and M. Makhorkin [9, 10] the problem of the limit equilibrium of a long cylindrical shell with a longitudinal crack under the action of a load varying in time with regard to the inertia of the material was considered. In [9], the methodology for constructing a system of singular integral equations (SIE) to determine the coefficients of intensity of forces and moments at the tips of a crack is described, and in [10], such a system is constructed and ways to solve it are proposed. The following is a study of the effect of load's variation rate on the values of the intensity coefficients of forces and moments in cylindrical shells with a longitudinal crack based on the relations obtained in [10] and the influence of shell parameters (physical and geometrical) on its limit equilibrium is analyzed.

2. Problem formulation

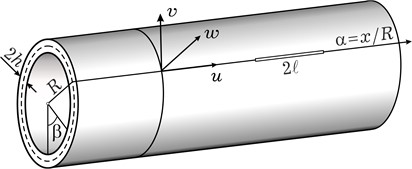
An infinite cylindrical shell of radius $R$ with a through longitudinal crack of length $2\mathcal{l}$ was considered (Fig. 1). The shell is under the action of a surface loading that varies according to an exponential law $e^{\tilde{\gamma }\tau }$ and the location of the crack does not violate the Saint-Vernand principle

According to [2, 3], as it was realized in [9, 10], we write:

– The corresponding efforts that will take place in the shell:

– Stress-free deformation field:

– Conditions on the crack edges [10]:

where:

where ${\epsilon }_{ij}^{*}$, ${\mathrm{\ae }}_{ij}^{*}$, $i,j=\alpha ,\beta$ are the coordinate functions; $\left[u\right(\alpha ,\tau \left)\right]=\left[u^{*}\right(\alpha \left)\right]e^{\tilde{\gamma }\tau }$, $\left[v\right(\alpha ,\tau \left)\right]=\left[v^{*}\right(\alpha \left)\right]e^{\tilde{\gamma }\tau }$, $\left[w\right(\alpha ,\tau \left)\right]=\left[w^{*}\right(\alpha \left)\right]e^{\tilde{\gamma }\tau }$, $\left[{\theta }_{\beta }\right(\alpha ,\tau \left)\right]=\left[{\theta }_{\beta }^{*}\right(\alpha \left)\right]e^{\tilde{\gamma }\tau }$ are functions of displacement jump and rotation angles, respectively; $\tau =t/T$ is the dimensionless time; $T=\pi R/v_{\tau }$ is the time for an elastic wave to traverse half of the shell circumference; $v_{\tau }=\sqrt{E/\rho }$ is the velocity of elastic wave propagation in the shell material; $E$ is the Young’s modulus of the shell material; $\rho$ is the density of the shell material; $\tilde{\gamma }$ is constant coefficient that characterizes the rate of growtes of the load; $\delta (\cdot )$ is the Dirac delta function; ${\partial }_j^n={\partial }^n/\partial j^n$, $n=\mathrm{1,2},3,\dots$, $j=\alpha ,\beta ,\tau$; $N_2^0$, $S_{}^0$, $Q_2^{0*}$, $M_2^0$ – are the normal, shear, and generalized shear forces and the bending moment in a shell without a crack respectively; $N_2^1$, $S_{}^1$, $Q_2^{1*}$, $M_2^1$ are the similar efforts applied to the real crack edges; corresponding forces and moments on the edges of a notch $\beta =\pm 0$ are marked by the superscripts “$+$” and “$-$”.

In the case of a complex value of $\tilde{\gamma }=\mathrm{R}\mathrm{e}\tilde{\gamma }+i\mathrm{I}\mathrm{m}\tilde{\gamma }$, we will come to the formulation of the problem for a load that varies harmonically according to the law of cosine or sine. In this formulation of the problem, it is necessary to consider the equality of their real (cosine law) or imaginary (sinusoidal law) parts in Eqs. (1-3).

The system of equilibrium equations in displacements that takes into account the inertia of the material in accordance with [2, 4, 9] is as follows:

where $c_{\tau }^2=v_{\tau }(1-{\nu }^2)$; $\nu$ is the Poisson’s ratio; we do not give the expressions for $L_{k1}$, $L_{k2}$, $L_{k3}$ because of their cumbersomeness (they can be found in [10]).

3. Construction of a problem solutions

In [9] is given detailed presentation of the methodology for solving the formulated problem and the procedure of constructing a system of singular integral equations, the solution of which makes it possible to calculate the dynamic coefficients of intensity of forces and moments near the tips of the crack. Since the above expressions are extremely cumbersome, we do not present them in this paper.

Fig. 1Сylindrical shell with a longitudinal crack

The intensity factors (IF) of forces and moments are given as follows [10]:

where:

where the functions ${\mathrm{\Omega }}_1\left(u\right)$, ${\mathrm{\Omega }}_3\left(u\right)$ are solutions of the singular integral equations system [10]:

Also, [10] describes in detail all the steps of constructing these singular integral equations (SIE) system and provides expressions for all the necessary functions.

In Eq. (6) the factor $e^{\tilde{\gamma }t}$ characterizes the variation of the value of the intensity factors of forces and moments depending on the time of load action, the parameter $\tilde{\gamma }$ describes the rate of the load’s variation, and $\frac{1}{2}\sqrt{\mathcal{l}}{K}_N^0$, $\frac{1}{2}Rc\sqrt{\mathcal{l}}{K}_M^0$ take into account the geometric and physical parameters of the shell as well as the load’s variation rate.

Similarly to [2, 3] to estimate the intensity of forces and moments, we will use relative intensity factors for dynamic loading $K_N^0=\frac{2K_N}{\sqrt{\mathcal{l}}}{e}^{-\tilde{\gamma }t}$ and $K_M^0=\frac{2K_M}{Rc\sqrt{\mathcal{l}}}{e}^{-\tilde{\gamma }t}$. These factors describe, respectively, the intensity of efforts and moments in a period of time $t<T$.

4. Numerical results and discussion

Based on the constructed in [10] solutions of the SIE system Eq. (8) and on the relationships Eq. (7), the dependence of the relative IF of forces and moments on the rate of load variation and crack length was studied.

The study was carried out for a cylindrical shell with a longitudinal crack under the following assumptions:

1) The radius of the shell and its thickness are respectively equal to $R=$15×10^-2 m, $h=$15×10^-4 m;

2) To the sides of the crack are applied the following forces and moments with constant intensity $N_2(\alpha ,0,\tau )=-N^0{e}^{\tilde{\gamma }\tau }=e^{\tilde{\gamma }\tau }$ and $M_2(\alpha ,0,\tau )=-M^0{e}^{\tilde{\gamma }\tau }=0$.

3) The shell can be made of one of the following materials: steel ($E=$2×10¹¹ Pa, $\nu =\text{0.25}$, $\rho =$8×10³ kg/m³), copper ($E=$1.1×10^11 Pa, $\nu =\text{0.34}$, $\rho =$8.9×10³ kg/m³), cast iron ($E=$1×10¹¹ Pa, $\nu =\text{0.22}$, $\rho =$7×10³ kg/m³).

4) The approximate value of the time for which an elastic wave traverses the perimeter of such shell, depending on its material, is equal to $T_{st}=$0.9×10^-4 for steel, $T_{cop}=$1.3×10^-4 for copper and $T_{c-iron}=$1.2×10^-4 for cast iron.

The research results are presented graphically in Figs. 2-4, where the dashed curves correspond to the values calculated for the shell made of cast iron, dotted curves - of copper, solid curves – of steel.

The relative dynamic IFs of forces (Fig. 2(a), Fig. 3(a)) and moments (Fig. 2(b), Fig. 3(b)) at low load growth rates $\tilde{\gamma }<\text{0.01}$ are different from the corresponding relative IFs at static load [2, 3] no more than 1 %, which indirectly confirms the reliability of the performed studies. With an increase in the loading rate, the relative force intensity factor decreases approaching a certain limit value, which depends on the crack length. The critical value of the loading rate, after which the values of the dynamic IF begin to differ by more than 5 % from the values of the static IF, depends on the length of the crack (decreases with its prolongation).

Fig. 2Dependence of relative intensity factors of forces KN0 and moments KM0, on the relative crack length α0=l/R for values of the loading rate γ~

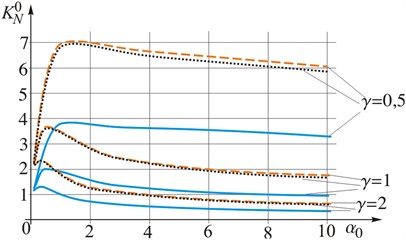
a) Relative IF of the efforts

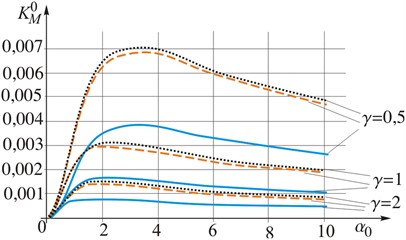
b) Relative IF of the moments

Fig. 3Dependence of the relative intensity factors of forces KN0 and moments KM0 on the rate of load variation γ~ for different values of the relative crack length α0=l/R

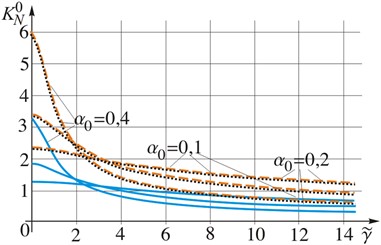
а) Relative IF of the efforts

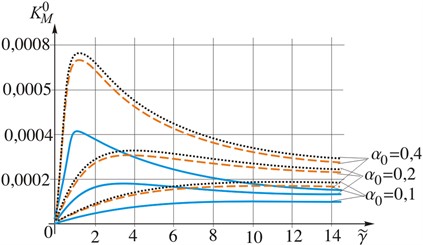
b) Relative IF of the moments

Based on the analysis of SIE kernels in [9], was made an assumption, that it is possible to neglect the influence IF of moments when estimating the strength of the shell and predicting its fracture. The results of calculations of the values of relative IF of forces (Fig. 2(a), Fig. 3(a)) and values of IF of moments (Fig. 2(b), Fig. 3(b)) confirm this assumption. The diagrams show that the moments IF are more than three orders of magnitude smaller than the corresponding forces IF, and therefore have little effect on the overall picture of the limit equilibrium

The value of the relative dynamic IF of moments (Fig. 2(b), Fig. 3(b)) increases with increasing loading rate. The graphs clearly show local maxima at the critical load rate, after which the IF values decrease towards a certain asymptote. Note that the critical rate is greater if the longer the crack length is, and the asymptotic value of the relative dynamic IF is higher than the value of the corresponding relative IF of moments under static loading (at low rates of loading $\tilde{\gamma }<\text{0.01}$).

The respective diagrams show that the relative force and moment intensity factors for shells made of materials such as copper and cast iron are similar in their values. At the same time, they are twice as much as the corresponding values for the steel shell. A comparison of the mechanical characteristics of the respective materials allows us to conclude that the value of the Young’s modulus has a predominant influence on the magnitude of the relative dynamic IF of forces and moments.

An illustration of the influence of the relative dynamic factor on the overall pattern of changes in the values of the dynamic force factor $K_N=0.5\sqrt{\mathcal{l}}{K}_N^0{e}^{\tilde{\gamma }\tau }$ is shown in Fig. 4. It shows the dependence on the relative time ($0\le \tau \le 1$) of the actual dynamic intensity factors of forces (Fig. 4(a)) and their exponential time dependence $e^{\tilde{\gamma }\tau }$ (Fig. 4(b)) in a steel shell with a longitudinal crack (crack length ${\alpha }_0=\text{3.85}$) at different loading rates $\tilde{\gamma }=\text{0.5}$, $\tilde{\gamma }=\text{1}$, $\tilde{\gamma }=\text{2}$. The analysis of the presented graphs demonstrates that for an adequate qualitative and quantitative assessment of the value of dynamic intensity factor of forces and moments, it is necessary to take into account the value of the relative IF at the initial stage of loading.

Fig. 4Time dependence of dynamic intensity factors of forces and their exponential time dependence in a steel shell with a longitudinal crack

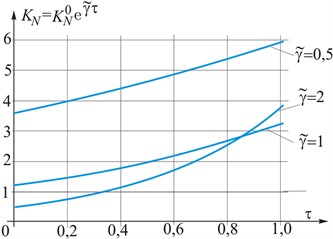
a) Dynamic intensity factors of effort

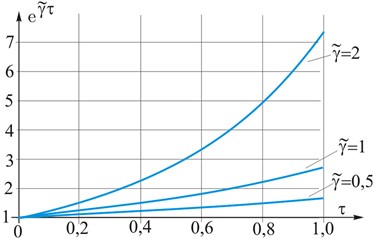
b) Exponential dependence

5. Conclusions

It is confirmed that the written in the explicit form system of singular integral equations with the Cauchy kernel [10] can be successfully used to determine the stress-strain state of cylindrical shells with a longitudinal crack under the action of a time-varying load. The reliability of the research is confirmed by the coincidence of the results of calculations at low rates of load variation with the known results for the case of static load [2, 3].

The effectiveness of the constructed algorithm for numerical solution of the system of equations obtained in [10] is confirmed.

The intensity factors of forces and moments near the tips of a longitudinal crack in the cylindrical shell under the action of a varying in time according to an exponential law load (this type of load occurs, for example, at a water hammer) are calculated. The corresponding intensity factors were calculated for shells made of different materials (copper, steel, cast iron).

The analysis of the obtained results is carried out, the main results of which are as follows:

– The Young’s modulus has a predominant influence on the magnitude of the dynamic intensity factor.

– At low rates of load variation, the effect of taking into account the inertia of the material when calculating the relative coefficients of force intensity can be neglected.

– The intensity factors of moments are more than three orders of magnitude smaller than the corresponding forces intensity factors, and therefore have a small effect on the overall picture of the limit equilibrium.

– With an increase in the rate of load variation, the IF of forces and moments approach to a certain asymptotic value.

The results of the studies confirm the effectiveness of the methods proposed in [9, 10] for determining the stress-strain state of cylindrical shells with longitudinal cuts under the action of a time-varying load. In the future, they can be used to determine the opening of the crack and estimate the strength of the shell.