Dynamic stress intensity factor of a finite crack based on a fractional differential model

1. Introduction

The increasing use of polymers and concrete demands an understanding of the response of cracked viscoelastic body to vibrational load. Rosakis et al. discovered cracks in a polymer, loaded under shear, propagate faster than the speed of shear waves [1]. Motivated by the experimental observations, it is desirable to make a study of cracks, loaded dynamically, in viscoelastic materials. Computation of the stress intensity factor (SIF) is one of the key tasks in fracture analysis. Dynamic stress intensity factors (DSIFs) of cracks imposed by dynamic load in viscoelastic materials have been explored by some researchers [2-6].

Previous work on DSIFs is mainly concerned with viscoelastic materials whose equation of motions are given in the form of wave equations, and constitutive equations are given in the form of various models of integer linear viscoelasticity, which are ‘‘integer differential” viscoelastic model and variations of them, however, they are not sufficiently accurate for more complex materials, i.e. some polymer. Recently the “fractional differential” models have been investigated for viscoelastic materials by a number of researchers [7, 8].

DSIFs of Mode III semi-infinite crack in a viscoelastic medium have been obtained by four parameters Bagley-Torvik fractional differential constitutive models [9]. This paper deal with the mode III finite length crack in a viscoelastic medium based on the fractional differential constitutive models.

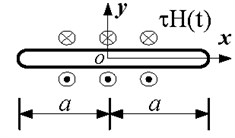
2. Formulation of the problem

The basic equations of finite Mode III crack in viscoelastic medium consist of equation of motion as shown in Fig. 1.

Fig. 1Finite Mode III crack in a viscoelastic medium

Strain-displacement relations:

and constitutive equations defined by extending the one-dimension Bagley-Torvik fractional differential model to two-dimension [10, 11]:

where $\alpha$, $\beta$ (0 $<\alpha$, $\beta <$ 1) is the order of the fractional derivative and $b_1$, $b_2$ ($b_1$, $b_2\ge$0) are parameters. Obviously, when $b_1=b_2=$0, Eqs. (3), (4) are equal to the linear elastic constitutive relationships.

There are various definitions of fractional integration and differentiation, such as Grunwald-Letnikov’s definition, Riemann-Liouville’s defintion, Caputo’s definition [12-14]. For the purpose of this paper, the Caputo’s definition of fractional integration and differentiation will be used, taking the advantage of Gaputo’s approach that the initial conditions for fractional differential equations with Caputo’s differentiation take on the same form as for integer-order differential equations [13, 14]:

where the parameter $\eta$ is the order of fractional differentiation.

The Laplace transform of $f\left(t\right)$ and its inverse formula are defined by:

The Laplace transform of the Caputo’s fractional derivative can be written as [14]:

Taking the derivation of the Eqs. (3), (4) with respect to $x$, $y$, we have:

The fractional wave-like equation can be obtained [9]:

where $c=\sqrt{\mu /\rho }$.

For the finite length crack, the boundary conditions are:

where $\tau$ is the amplitude of the anti-plane shear load, $H\left(t\right)$ is Heaviside unit step function and crack length is $2a$.

The initial conditions are:

3. Dynamic stress intensity factors

Taking the Laplace transform of the Eq. (10) with respect to $t$, we have [9]:

where ${\xi }^2=1+b_1{p}^{\alpha }/\left(1+b_2{p}^{\beta }\right),\left(\xi >0\right).$

The Fourier transform and its inverse transform is:

Taking the Fourier transform of the Eq. (15) with respect to $x$, we have:

The solution to the Eq. (17) by applying the boundary condition Eq. (13) is:

where ${\gamma }^2={\left(\xi p/c\right)}^2+s^2$, ($\gamma >$ 0).

The Laplace transform to Eqs. (11) and (12) gives by using the symmetry:

Taking the inverse Fourier cosine transform of the Eq. (18), we have [15]:

Eqs. (19) and (21) can be applied to lead to:

The Laplace transform to Eq. (9) with applying the Eq. (2) leads to:

From Eq. (20) and (23), we find:

Eqs. (20) and (23) form a pair of dual integral equations. The function $C(s,p)$ is defined by:

The dual integral equations can be solved by a Fredholm integral equation of the second kind [15]:

where:

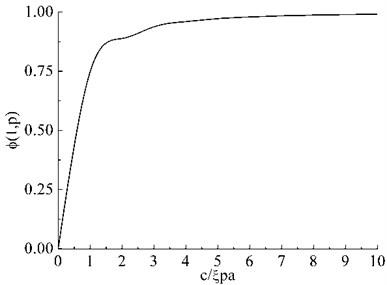
where $J_0$ is a zero order Bessel function. Fredholm integral equation Eq. (26) is treated by the composite Simpson of rules to obtain ${\mathrm{\Phi }}_3^{\mathrm{*}}(1,p)$, the numerical solution to Eq. (26) can be found in Appendix ${\mathrm{\Phi }}_3^{\mathrm{*}}(1,p)$ is function of $c/\xi pa$ which can be seen in Fig. 2.

Fig. 2Solution of Fredholm equation for finite Mode III crack

The DSIF of cracked viscoelastic body can be found [15]:

From Eq. (1), the viscoelastic DSIF is equal to elastic DSIF when $1+b_1{p}^{\alpha }=1+b_2{p}^{\beta }$.

The Miller and Guy numerical inverse Laplace transform is used for Eq. (1).

4. Numerical results

Let $K_3^{\#}\left(t\right)=K_3/\tau \sqrt{\pi a}$. Numerical results for the dynamic SIF were obtained for 4 cases:

– Case a: $b_1=b_2=$8, $\beta =\mathrm{}$0.5, $\alpha =\mathrm{}$0.25, 0.5, 0.75.

– Case b: $b_1=b_2=\mathrm{}$8, $\alpha =\mathrm{}$0.5, $\beta =\mathrm{}$0.25, 0.5, 0.75.

– Case c: $\alpha =\beta =\mathrm{}$0.5, $b_1=\mathrm{}$8, $b_2=\mathrm{}$4, 8, 12.

– Case d: $\alpha =\beta =$ 0.5, $b_2=$ 8, $b_1=$ 4, 8, 12.

Fig. 3Viscoelastic DSIF time history for different cases

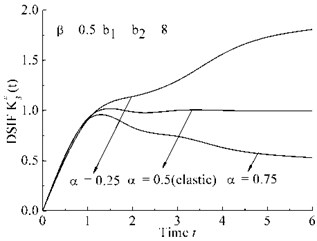
a) Case a

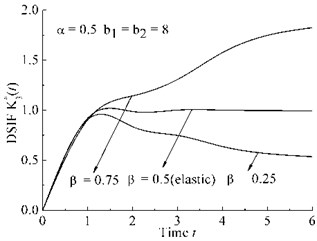
b) Case b

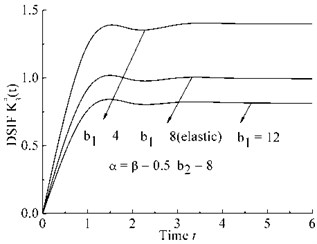
c) Case c

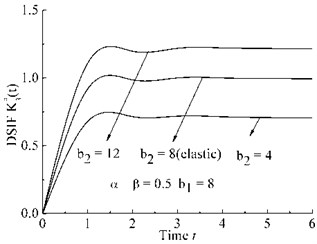
d) Case d

As shown in Fig. 3(a)-Fig. 3(d), DSIFs are proportional to the parameters $\beta$, $b_2$, and inversely proportional to the parameters $\alpha$, $b_1$.

As shown in Fig. 3(a)-Fig. 3(b), The fractional differential order have strong effects on the viscoelastic DSIF after DSIF curves reach the peak of time history curve. When fractional order $\alpha >\beta$, the curve is negative gradient, while when $\alpha <\beta$, the curve is negative gradient after the peak of DSIF time history.

As shown in Fig. 3(c)-Fig. 3(d), parameters $b_1$, $b_2$ have little effect on the gradient of the DSIF curves after peak of DSIF curve.

5. Conclusion

Bagley-Torvik fractional differential model are introduced to obtain a fractional wave-like equation for finite Mode III crack. Bifurcation phenomenon of viscoelastic DSIF can be observed by choosing appropriate fractional differential order $\alpha$, $\beta$. Parameters $b_1$, $b_2$ have some effect on amplitude of viscoelastic DSIF curve but little effect on the gradient of viscoelastic DSIF after the peak of the DSIF curve.