Abstract
To predict residual lifetime of ball screw, screw lifetime prediction technology based on wavelet neural network (WNN) and empirical mode decomposition (EMD) is proposed. Screw accelerated lifetime test platform is introduced. Accelerometers are installed to monitor ball screw lifetime. With the method of principal component analysis (PCA), high dimension features are mapped to low dimensional space and stored into sample library together with screw expected remaining lifetime. Training samples and testing samples are randomly selected from the sample library to train and test the WNN. Then EMD is used to extract output tendency of WNN. Finally, screw lifetime prediction model can be obtained. The experimental results show that the maximum error of the training samples is 602 hours while the maximum error of the testing samples is 652 hours, which meet the need of screw lifetime prediction.
1. Introduction
With the increase of market competition, maximized production and minimized cost are required by modern manufacturing industry [1-3]. We can see that the comprehensive monitoring of the manufacturing process would become an inevitable trend. As a key component of NC machine tool, ball screw directly affects NC machine tool’s manufacturing accuracy [4, 5]. Therefore, it is necessary to predict the remaining lifetime of ball screw so as to minimize NC machine tool’s downtime. Aiming at this problem, a screw lifetime prediction model based on wavelet neural network (WNN) and empirical mode decomposition (EMD) is proposed. WNN is a neural network based on back propagation topology. Wavelet basis function is treated as the transfer function of hidden layer node. Considering screw remaining lifetime is a kind of trend variable, EMD is adopted to extract predicting trend from the output of WNN. Particularly, the screw accelerated lifetime test platform which used to imitate NC machining process is introduced. The experimental results show that proposed model can effectively predict the remaining lifetime of ball screw.
Fig. 1Screw accelerated lifetime test platform
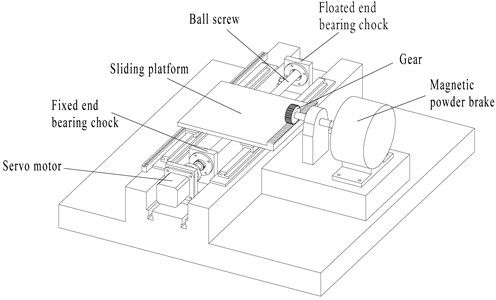
2. Screw accelerated lifetime test
Fig. 1 shows the screw accelerated lifetime test platform. A servo motor is used to drive the ball screw, while a magnetic powder brake is used as the ball screw load. By the gear and sliding platform mechanism, the axial load force of the ball screw can be transferred from the magnetic powder brake. Two one-way accelerometers are installed at two bearing chocks while a three-way accelerometer is installed on the screw nut. Beckhoff EL3632 modules acquire the vibration signal with the sampling frequency of 5 kHz. Industrial PC is connected with the EL3632 modules and stores the vibration data. Ball screw reaches 40 mm in axis diameter, 5 mm in lead, 500 mm in journey. The installation method of the ball screw is one end fixed while the other end floated.
3. Vibration feature vector
3.1. Dynamic clustering data processing technology
Screw performance degradation is a long process. Condition monitoring of the performance degradation in total life cycle of the ball screw is necessary. To avoid the omission of information, data acquisition should be working during the total life cycle. This paper adopts dynamic clustering data processing technology to reduce redundant data. The basic idea is designing a flexible rectangular window to process data online [6]. By continuously moving the rectangular window in the signal, the signal can be compressed so the redundant data are eliminated.
The original signal can be expressed as {; 1, 2,…, }. New signal after clustering can be defined as {; 1, 2,…, }, where . and are used to express the length and width of the rectangular window respectively. In the premise of , the new signal after clustering can be expressed as:
When or , . Where is the maximum length of the rectangular window. The maximum length and width can be adjusted according to the experimental environment.
3.2. Feature extraction
The original features are extracted by following methods. With the method of wavelet analysis, the vibration signal is decomposed into 5 levels selecting wavelet “db1”, and distinct time-frequency features based on wavelet packet energy are extracted as a part of the original features. Time domain or frequency domain features are also been applied to rich the original features. Considering the certain correlation among the high dimensional original features, principal component analysis (PCA) is applied to eliminate redundant information.
4. Screw lifetime prediction model
4.1. Wavelet neural network
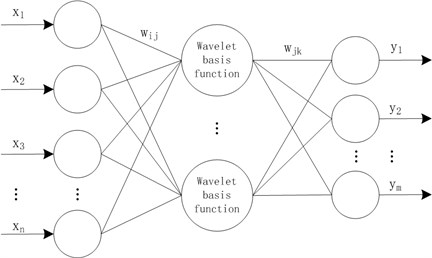
Topology of WNN is shown in Fig. 2. , ,…, is the input of WNN, while , ,…, is the output of WNN. and are the weight of WNN [7].
The output of hidden layer can be expressed as:
where 1, 2,…, and is the number of hidden nodes. is wavelet basis function. and are the displacement factor and scale factor of the wavelet basis function, respectively.
The output of WNN can be defined as:
where 1, 2,…, and is the output of neural network.
Fig. 2Topology of wavelet neural network
4.2. Empirical mode decomposition
Since screw remaining lifetime is a kind of trend variable, this paper adopts EMD to extract predicting trend from the output of WNN. The decomposition principle of EMD is defined as follows:
Step 1: searching all the local peaks of raw data sequence . Using cubic spline to envelope all local maximum points and minimum points, respectively. Sequence is the mean value sequence of two envelope curves.
Step 2: subtracting from and getting a sequence . Repeating above steps until is an intrinsic mode function, then is the first intrinsic mode function and defined as .
Step 3: subtracting from and getting a residual sequence .
Step 4: treating as a new raw data sequence. Repeating above steps until is a monotonic function. The raw data sequence can be expressed by some intrinsic mode functions and a mean trend:
where are the intrinsic mode functions and is the mean trend.
4.3. The structure of lifetime prediction model
Ball screw rated lifetime can be defined as:
where is the rated revolution of ball screw and is the rotational speed of ball screw. Then:
where is the expected remaining lifetime of ball screw and is the servicing lifetime.
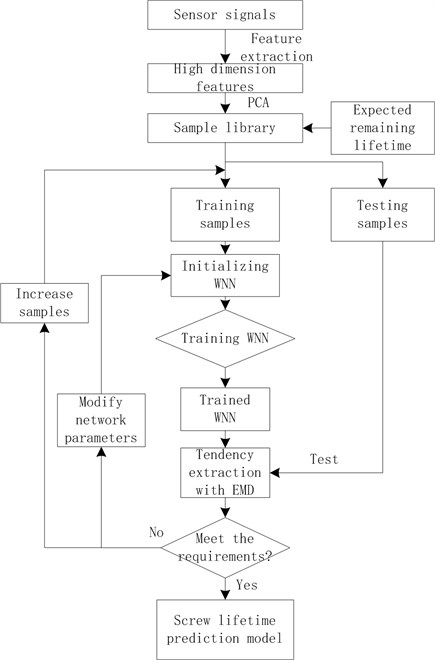
Fig. 3 shows the flow chart of building screw lifetime prediction model. By different feature extraction methods, high dimension features are extracted from sensor signals. Then feature vectors, which dimensions are reduced by PCA, are obtained and stored in feature vectors sample library together with their expected remaining lifetime. Training samples are randomly selected from the sample library to train WNN, while EMD is adopted to extract the output tendency of GNN. Testing samples are used to test the tendency accuracy. By means of increasing samples and modifying network parameters, prediction accuracy is ensured. Then screw lifetime prediction model can be obtained.
Fig. 3Flow chart of building prediction model
5. Experimental results
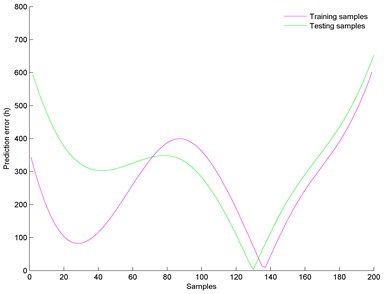
Total 200 samples are randomly chosen from the sample library together with their expected remaining lifetime. Training samples include 100 samples while testing samples include 100 samples. Parameters of the WNN are selected as follows: Morlet wavelet is selected as wavelet basis function. The number of the iterations is 100, while the number of nodes in hidden layer is 6. The prediction results of screw lifetime prediction model are shown in Fig. 4, while Fig. 5 shows the prediction error of the model. It is clear that the maximum error of the training samples is 602 hours while the maximum error of the testing samples is 652 hours. Compared with the ball screw rated lifetime, these errors are acceptable. The results indicate that the proposed model can predict screw residual lifetime effectively.
Fig. 4Screw residual lifetime prediction results
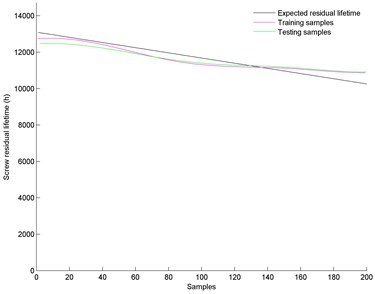
Fig. 5Prediction error of the proposed model
6. Conclusions
Screw lifetime prediction based on WNN and EMD is studied in this paper. Some conclusions can be obtained as follows:
1) Screw accelerated lifetime test platform can imitate NC machining process and shorten accelerated test time effectively;
2) Dynamic clustering data processing technology can be used to reduce redundant data during data acquisition process;
3) EMD can be applied to extract output tendency of WNN. From experimental results, it is clear that screw lifetime prediction model presents a good prediction accuracy.
References
-
Zhu S. W., Ding G. F., Qin S. F., Lei J., Zhuang L., Yan K. Y. Integrated geometric error modeling, identification and compensation of CNC machine tools. International Journal of Machine Tools and Manufacture, Vol. 52, Issue 1, 2012, p. 24-29.
-
Khan A. W., Chen W. Y. A methodology for systematic geometric error compensation in five-axis machine tools. International Journal of Advanced Manufacturing Technology, Vol. 53, Issue 5, 2011, p. 615-628.
-
Georg K., Thomas R. Industry 4.0-the next revolution in the industrial sector. Zkg International, Vol. 67, Issue 11, 2014, p. 30-32.
-
Tsai P. C., Cheng C. C., Hwang Y. C. Ball screw preload loss detection using ball pass frequency. Mechanical Systems and Signal Processing, Vol. 48, Issue 1, 2014, p. 77-91.
-
Hu J. Z., Wang M, Zan T. The kinematics of ball-screw mechanisms via the slide-roll ratio. Mechanism and Machine Theory, Vol. 79, Issue 1, 2014, p. 158-172.
-
Zhang X. C., Gao H. L., Huang H. F., Guo L., Xiao S. D. Optimization design of mathematical morphology filter based on quantum genetic algorithm. Journal of Southwest Jiaotong University, Vol. 49, Issue 3, 2014, p. 462-469.
-
Chen Y. B., Lee Y. L., Hsu S. J., Chen Y. W. Design of active heat dissipation system for adaptive wavelet neural network control. Neural Network World, Vol. 24, Issue 4, 2014, p. 395-410.
About this article
The authors would like to extend their thanks to the joint financial support by National Natural Science Fund of China (51275426).
