Analysis of the dynamic stiffness and bearing capacity for pile foundations

2.1. Dynamic loading test

To investigate the relation between the integrity and allowable capacity of piles, four model piles (P1-P4) with different defects were designed and constructed in the same test field. All the piles have the same diameter of 0.6 m, length of 11.2 m, reinforcement ratio of 0.4 %, and the concrete compressive strength class of C25. The pile P1 and P2 were designed with necking defects. The different size of necking formworks were bound with the reinforcement at the location of 5 m and 4 m from the pile top, respectively. The pile P3 was designed as a broken pile. A foam board was placed at the location of 5 m from the pile top. The pile P4 was designed with the segregation. The sand with 30 mm thick was constructed at the location of 5 m from the pile top.

All the pile head were polished. The low-strain integrity test was performed with a hand held hammer (Fig. 1(a)). The mechanical mobility method test was performed with a drop hammer, weighting 106 kg (Fig. 1(b)).

Fig. 1The dynamic loading test for model piles

a) Low-strain integrity test

b) Mechanical mobility method test

Fig. 2 shows the test results of the pile integrity. It can be found that: (1) pile P1 has a necking defect at the location of 5.52 m from the pile top; (2) pile P2 has an obvious necking defect at the location of 4.37 m from the pile top; (3) pile P3 is a broken pile and (4) pile P4 is a segregation pile.

By the mechanical mobility method test, according to Eq. (1), the averaged $K_d$ in the low frequency range for the four tested piles were 4.77×10⁸, 3.66×10⁸, 3.49×10⁸ and 1.35×10⁸ N/m.

Fig. 2The pile integrity test results

a) Pile P1

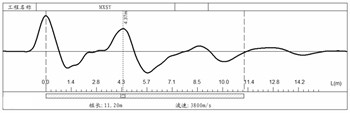
b) Pile P2

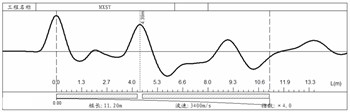
c) Pile P3

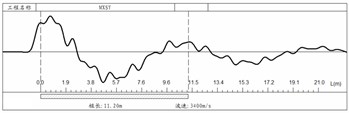
d) Pile P4

2.2. Static loading test

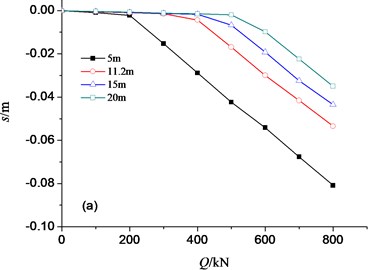
Two piles (P2 and P3) were selected to perform the static loading test. The loading test equipment with type JCQ-503A was used. The large concrete cubes were used to apply load (Fig. 3). Fig 4 shows the $Q$-$s$ curve for the relation between load and settlement. The ultimate capacities for P2 and P3 can be calculated from $Q$-$s$ curve: 635.2 kN for P2 and 622.7 kN for P3.

Fig. 3The pile loading test

a) Heaped load by concrete cubes

b) The jack and sensors

Fig. 4The Q-s curve for pile P2

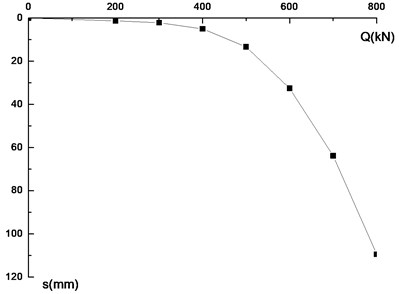
Fig. 5The stiffness and capacity for the test piles

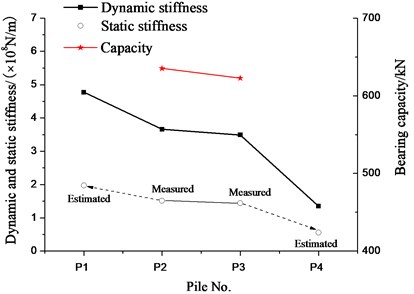
From the test result, the coefficient $\alpha =K_d/K_s$ can be calculated as 2.42 for both P2 and P3. Since all four piles were constructed in the same field, and had the same dimension, it can be regarded that all four piles have the same coefficient α. Then, the static stiffness $K_s$ for P1 and P4 can be estimated, shown in Fig. 5.

It can be found that, there was a positive relation between the dynamic stiffness and static stiffness for all four piles. Moreover, there was also a positive relation between capacity and dynamic stiffness for P2 and P3.

3.1. Dynamic analysis for the intact pile

A 3D pile-soil finite element model was built (Fig. 6). The pile was modelled with the elastic beam element, and with the same dimension with the tested model pile. The soil was modelled with elastic solid element. The measured impulse force signal was input, and response at the pile top can be obtained. Fig. 7 compares the measured and calculated mobility curves below 50 Hz. In low frequency range, the measured and calculated mobility curves match well.

Fig. 8 shows the dynamic stiffness changes with the pile length ($L_p$), pile diameter ($D_p$), Young’s modulus of the soil ($E_s$) and Young’s modulus of the pile ($E_p$). Results show that the pile length, pile diameter and the soil modulus have large influence on the dynamic stiffness, while the pile modulus has smaller influences on the dynamic stiffness of the pile.

Fig. 6The pile-soil finite element model

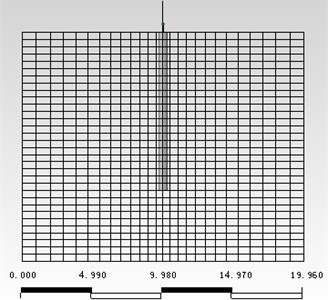
Fig. 7Mesured and calculated mobility

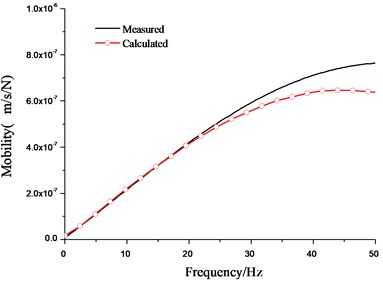
Fig. 8Calculated dynamic stiffness changes with different factors

3.2. Static loading analysis for the intact pile

A contact element was added between the pile-soil surface, and the Mohr-Coulomb yielding criterion was employed for the soil. Fig. 9 shows the soil displacement field. When the load is small, a settlement trough can be observed around the pile. The largest settlement was at the pile top. When the load reaches 400 kN, the soil settlement around the pile was obviously large. When the load reaches 600 kN, an obvious displacement can be observed at the pile bottom, which means a plastic flow occurs at the pile-soil contact surface.

Fig. 9Vertical displacement of soil under different loads

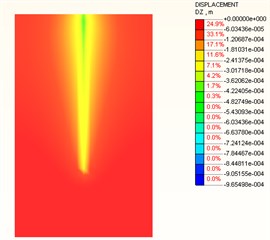
a) 200 kN

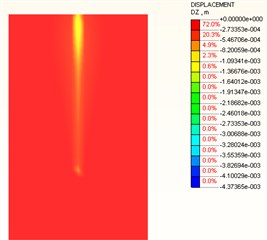
b) 400 kN

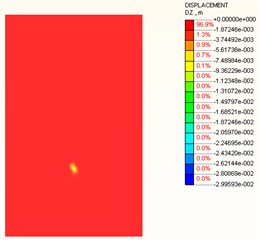
c) 600 kN

Similar to Section 3.1, the four parameters were analysed. Fig. 10 shows the $Q$-$s$ curves influenced by $L_p$, $D_p$, $E_s$ and $E_p$. The inflection point of the curve was affected by the pile length and diameter. Accordingly, the two parameters have the large influence on the $Q$-$s$ curve. The $E_s$ affect the slope after the inflection point, which also affect the pile ultimate capacity rather than the static stiffness. The parameter of $E_p$ has the least contribution to the $Q$-$s$ curve.

Fig. 10Load-settlement curves influenced

a)$L_p$

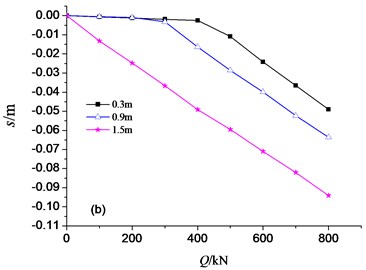
b)$D_p$

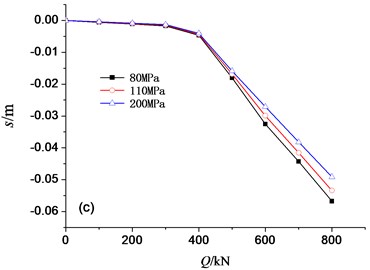
c)$E_s$

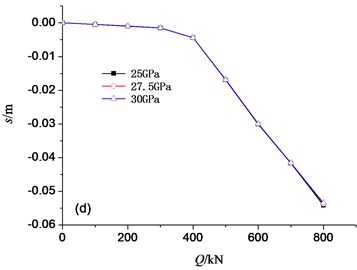
d)$E_p$

Fig. 11Parameter sensitivity analysis

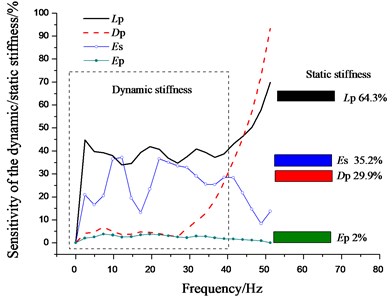
3.3. Parameter sensitivity analysis for the intact pile

The parameter sensitivity was shown in Fig. 11. Four parameters were considered to analyse the dynamic stiffness-frequency curve. Meanwhile, the parameter sensitivity for static stiffness was also plotted, by analysing the initial linear section of the $Q$-$s$ curves. It can be found that, in the early stage of the pile loading test, the deformation of pile-soil system is linear. The sequence of sensitivity for the dynamic and static stiffness kept the same. That is, when the pile capacity was controlled by pile displacement, the dynamic test can reflect the static characteristics well to the pile under elastic deformation.