Simulation analysis of seismic dynamic response of small interval tunnel in deep backfill area based on model test

1. Introduction

In the early stage of mountain city construction, due to the extensive use of the method of “opening mountains and filling valleys”, a large number of soil and stone mixed backfill areas were formed. With the development and utilization of urban underground space and the needs of rail transit construction, some sections of some lines will inevitably cross the deep backfill area mixed with soil and stone, which will bring certain risks to the design, construction and operation of the project.

Many scholars at home and abroad have compared model test with numerical simulation analysis to analyze the law of seismic dynamic response. H. H. Wei [1] verified the correctness of the modeling method by simulating shaking table test, and carried out three-dimensional modeling calculation on this basis to study the dynamic response of surface-underground structure system; R. C. Gomes [2] compared the centrifuge test and numerical simulation results, and analyzed the differences between the two research methods in seismic dynamic response; J. Y. Niu [3] et al. Established the numerical simulation model of small interval tunnel on layered rock slope by using Midas software, and compared the numerical simulation results with the shaking table results; Z. Y. Yu [4] et al. Carried out shaking table test and established three-dimensional finite element model for comparative analysis, studied the seismic dynamic response of transfer subway station; C. Liu [5] studied the dynamic response of shallow buried biased multi arch tunnel under Wenchuan wave by combining shaking table test and numerical simulation. However, at present, there are few studies on the seismic dynamic response of tunnels in the deep backfill area of soil rock mixture, and few people study the seismic dynamic response characteristics of pile supported small interval tunnels.

In this paper, based on the subway section tunnel project, a three-dimensional finite element model of pile supported small interval tunnel in soil rock mixed deep backfill area is established on the basis of model test, the seismic dynamic response of tunnel lining structure and foundation pile is studied, and the bending moment, internal force and displacement response characteristics of tunnel lining and foundation pile under earthquake are analyzed, which can provide some reference for the design, construction, operation of similar projects.

2. Establishment of numerical model

2.1. Model size and material parameters

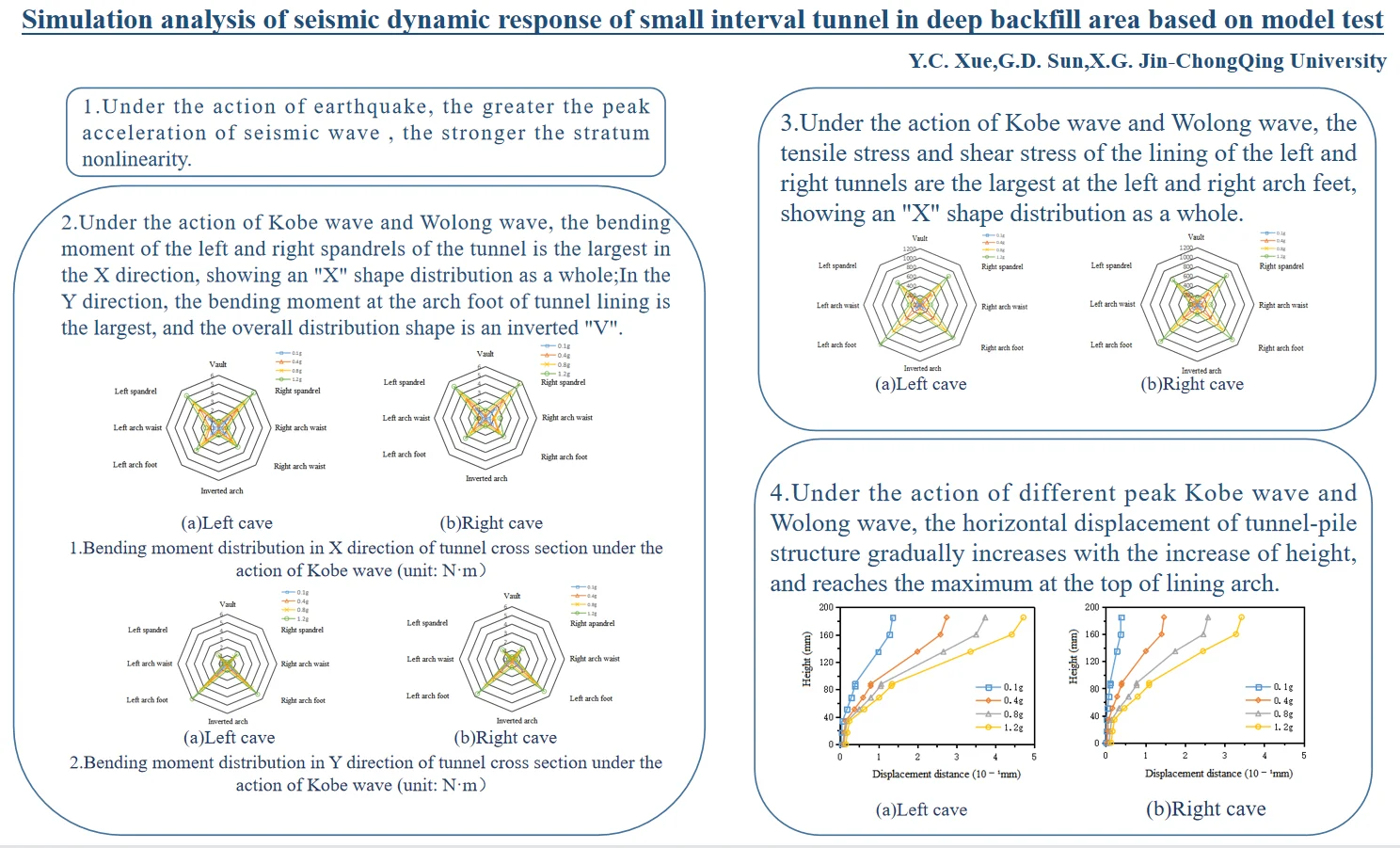
The numerical model is established based on the dimensions and material parameters of the model test. The length of the model is 0.95 m, the width is 0.8 m, the height is 0.65 m, the lining thickness is 6 mm, and the diameter of the tunnel foundation pile is 8 mm. The specific dimensions are shown in Fig. 1. The three-dimensional finite element model is shown in Fig. 2.

The surrounding rock of the model adopts Mohr Coulomb constitutive model, and the structure adopts elastic model. The physical and mechanical parameters of surrounding rock and structure are set according to the test results of similar materials. The specific parameters are shown in Table 1.

Fig. 1Marking drawing of model size (unit: mm)

Fig. 2Three dimensional finite element model

Table 1Physical and mechanical parameters of materials

Name	Density (kN/m³)	Cohesion (kPa)	Internal friction angle (°)	Elastic modulus (MPa)	Poisson ratio ($\mu$)
Earth rock mixture	18	0.8	33.2	0.8	0.3
Grout	20	8	38.5	3.5	0.28
Sandstone	24	50	41	62.5	0.25
Lining	15			2800	0.3
Pile	15			2800	0.3

2.3. Seismic wave input of mode

The processed Kobe wave collected in Kobe earthquake and Wolong wave collected in Wenchuan earthquake are selected in the simulation. Taking 0.1 g Kobe wave and 0.1 Wolong wave as examples, the peak acceleration curve of the input seismic wave is shown in Fig. 3.

Fig. 3Acceleration time history curve of seismic wave

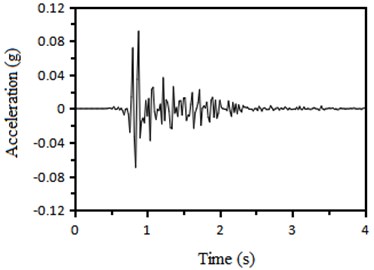
a) 0.1 g Kobe wave

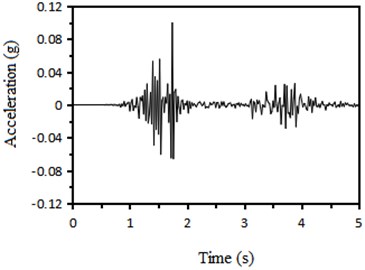
b) 0.1 g Wolong wave

3. Analysis of numerical simulation results

3.1. Acceleration response characteristics

Select the measuring points as shown in Fig. 4. Extract the acceleration data of each measuring point, and draw the variation curve of formation acceleration along the height direction under the action of different peak Kobe wave and Wolong wave as shown in Fig. 5. Under the action of Kobe wave, with the increasing peak acceleration of input seismic wave, the stratum nonlinearity gradually increases, which is most obvious at A14 measuring point. When the peak acceleration of input exceeds 0.4 g, the peak acceleration at A14 measuring point shows obvious “saturation” characteristics. When the peak acceleration of input is greater than 0.6 g, the stratum acceleration no longer increases monotonically along the height, Present an anti zigzag variation law; Under the action of Wolong wave, when the input peak acceleration exceeds 1.0 g, the formation acceleration presents a zigzag variation law along the height.

Fig. 4Schematic diagram of model acceleration measuring points

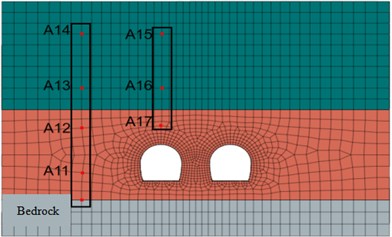
Fig. 5Variation curve of peak acceleration along height direction of the model under the action of different seismic wave

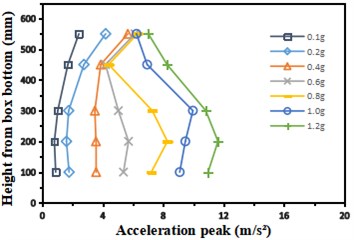
a) Kobe wave

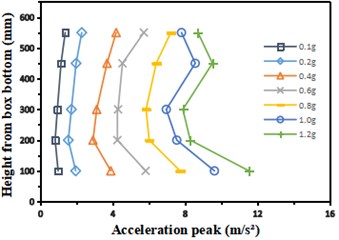
b) Wolong wave

3.2. Tunnel lining-pile response characteristics

3.2.1. Moment response of tunnel lining

Under the action of Kobe wave and Wolong wave with different peak intensities, the bending moment value of the left and right spandrels of the tunnel is the largest in the $X$ direction, followed by the left and right arch feet. The bending moment value generally presents an “$X$” shape distribution on the cross section of the lining; In the $Y$ direction, the maximum bending moment appears at the arch foot of the lining, followed by the left and right spandrels. The bending moment at the inverted arch and arch waist is small. The bending moment is distributed in an inverted “$V$” shape on the cross section of the lining.

Fig. 6Bending moment distribution in X direction of tunnel cross section under the action of Kobe wave (unit: N·m)

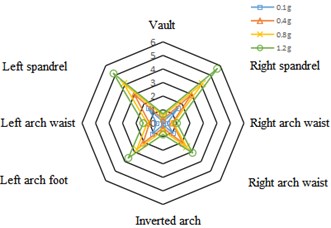
a) Left cave

b) Right cave

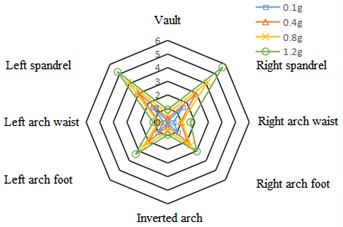
Fig. 7Bending moment distribution in Y direction of tunnel cross section under the action of Kobe wave (unit: N·m)

a) Left cave

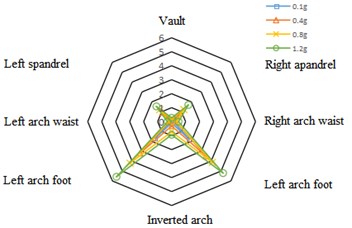
b) Right cave

3.2.2. Stress response of tunnel lining

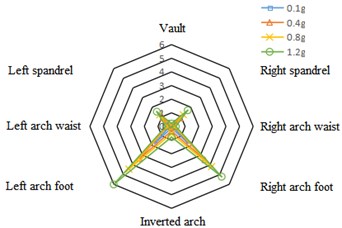
Under the action of the two kinds of seismic waves, the stress distribution in the left and right tunnel lining are the same. The maximum tensile stress and shear stress are at the left and right arch feet, followed by the left and right spandrels, and the vault and inverted arch are the smallest, showing an “$X$” shape distribution as a whole. Taking Wolong wave as an example, the maximum tensile stress distribution diagram of tunnel cross section is drawn, as shown in Fig. 8.

Fig. 8Maximum tensile stress distribution of tunnel cross section under the action of Wolong wave (unit: N·m)

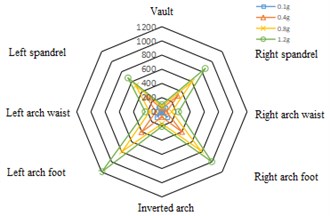
a) Left cave

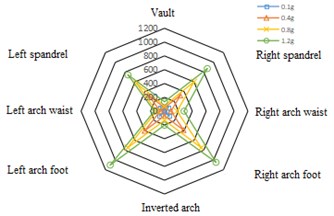
b) Right cave

3.2.3. Pile moment response

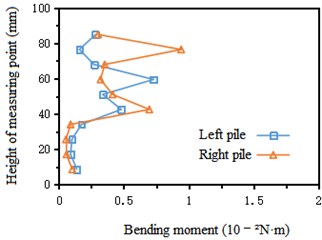
Under the excitation of Kobe wave and Wolong wave, the peak bending moment increases nonlinearly along the height of the pile. The bending moment of the pile in the sandstone stratum (height 0-33 mm) is generally small; The bending moment of the pile in the soil rock mixture stratum (height 33-85 mm) increases first, then decreases and then increases along the height. Take Kobe wave as an example to draw the curve of pile bending moment along the height, as shown in Fig. 9.

Six measuring points are selected at equal intervals from the bottom to the top of the pile body, and four measuring points are selected on the lining: arch foot, arch waist, arch shoulder and arch crown. The results of the selected measuring points are analyzed. It is found that under the action of different peak Kobe wave and Wolong wave, the horizontal displacement of tunnel-pile structure increases gradually with the increase of height, and reaches the maximum at the top of lining arch. It can be seen from Fig. 10 that there are two obvious turning points in the curve, which are located near the height of 30 mm and 90 mm respectively. Near the height of 30 mm, the change trend of relative horizontal displacement increases suddenly, because the stratum around the pile changes from bedrock to grouting body, and the horizontal displacement constraint of grouting body on the pile is much less than that of bedrock. The change trend of relative horizontal displacement also increases suddenly near the height of 90 mm. The reason is that the height of 85 mm is the junction point of pile foundation and tunnel lining. The overall bending stiffness of tunnel lining is greater than that of lining. Pile and lining are in the grouting stratum and belong to the same material, so the change trend of relative horizontal displacement along height is similar.

Fig. 9Variation curve of pile bending moment along height under the action of Kobe wave Horizontal displacement of tunnel-pile structure

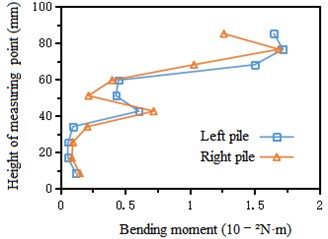
a) Left cave

b) Right cave

Fig. 10Variation curve of horizontal displacement of structure along height under Wolong wave

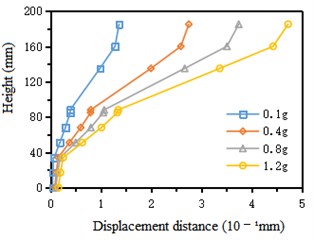
a) Left cave

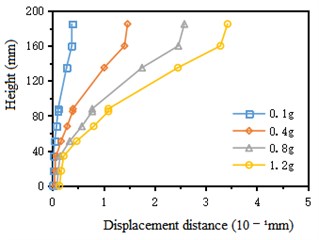
b) Right cave

4. Conclusions

1) Under the action of Kobe wave, the greater the peak acceleration of input seismic wave, the stronger the stratum nonlinearity. When the peak acceleration of input seismic wave exceeds 0.4 g, the stratum acceleration response of soil rock mixture appears obvious nonlinear characteristics.

2) Under the action of Kobe wave and Wolong wave, the bending moment of the left and right spandrels of the tunnel is the largest in the $X$ direction, showing an “$X$” shape distribution as a whole; The bending moment at the arch foot of the tunnel lining is the largest in the $Y$ direction, presents an inverted “$V$” shape on the cross section of the lining as a whole; Along the direction of pile height, the peak bending moment increases nonlinearly, and the bending moment in sandstone stratum is generally small. While in soil rock mixture stratum, the bending moment increases first, then decreases and then increases along the height.

3) Under the action of Kobe wave and Wolong wave, the tensile stress and shear stress in the left and right tunnel lining are the largest at the left and right arch toes, followed by the left and right arch spandrels, and the smallest at the arch crown and inverted arch, showing an “$X$” shape distribution as a whole.

4) Under the action of different peak Kobe wave and Wolong wave, the horizontal displacement of tunnel-pile structure gradually increases with the increase of height, and reaches the maximum at the top of lining arch.