Sloshing reduction in three-dimensional rectangular container using rigid baffles

1. Introduction

Sloshing is one kind of fluid motion in a partially filled moving container with a free surface. The free liquid surface can experience different types of motion like rotational, irregular, symmetric, and asymmetric. It will depend on the type of disturbance and container shape. Sloshing can result in serious damage to liquid storage tanks. Knowledge of natural frequencies and coupled frequencies is a must while dealing with large storage tanks, missiles, space vehicles. In most cases, the natural frequencies and control frequencies are very close which is dangerous for the structural integrity and stability of rockets, satellites, ships, and trucks. Shifting these frequencies is the only solution to this problem. This can be done by covering the free liquid surface with rigid baffles, flexible membranes, and movable devices. It reduces the sloshing mass participating in the dynamic response of the container. So, the concept of sloshing is always kept in mind while designing the storage tanks.

The subject of liquid sloshing in tanks is important to both transportation and seismic engineering. Liquid sloshing has a negative impact on the directional dynamics and safety performance of highway tank trucks. The stability limit and controllability of partially filled tank vehicles are reduced by hydrodynamic forces and moments coming from liquid cargo oscillations in the tank during steering and/or braking movements. Anti-slosh devices, such as baffles, are commonly employed to reduce the negative effects of liquid slosh on tank vehicle directional performance and stability. Liquid sloshing accounts for the majority of damages in liquid tanks during earthquakes, especially in long period and long duration ground motions. Anchorage earthquake of 1964, Niigata earthquake of 1964, Nihonkai-chubu (Japan sea) Earthquake of 1983, Izmit earthquake of 1999, Tokachi-oki Earthquake of 2003, and Tohoku earthquake of 2011 are examples of these catastrophic instances, which have been dubbed Natech in recent decades.

Sloshing can be a result of external forces due to the acceleration of the containment body. Over the years, a wide range of researchers has been studied the problem of sloshing using different methods and techniques. NASA reported the first comprehensive reference about sloshing, after it many researchers presented analytical, numerical, and experimental studies of sloshing. Many of these studies are cited by Ibrahim [10]. Baffles are used as slosh dampers in liquid storage tanks. The baffle effect on the dynamics of sloshing is reported in [1], [2], [5], [7], [8], [13], [17], [18], and [19]. Effects of perforated and porous baffles on reducing sloshing in tanks are studied in [15] and [16]. Some works have been reported where flexible membranes are considered to discuss sloshing. These studies on flexible membranes are presented in [4]. A lot of experiments and analyses have been performed previously in recent years for circular cylindrical containers with inviscid liquid. Some of these analyses and experiments are shown in [3], [6], and [12]. Some studies to reduce the floating roof motion during earthquakes are reported in [11] and [14]. Effect of vertical baffles on $2$-$D$ liquid sloshing characteristics in a partially filled rigid horizontal cylindrical container of an elliptical cross-section is investigated in [9].

Many researchers are trying to reduce the sloshing in tanks using different damping devices. In the present paper, the effects of a rigid baffle placed on the free surface of liquid have been analyzed on sloshing frequencies.

2. Statement and formulation of the problem

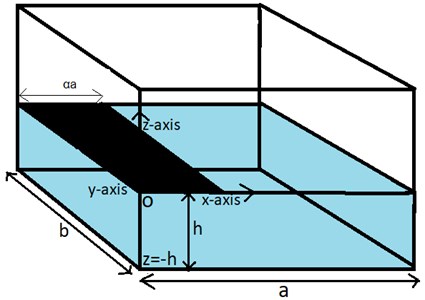
A rigid three-dimensional rectangular container with length $a$, breadth $b$, and height $h$ corresponding to the $x$-axis, $y$-axis, and $z$-axis respectively, which is partially filled with an incompressible and inviscid fluid up to height $h$, is considered. The free surface of the liquid is covered partially by a rigid baffle of width $\alpha a$ from the left side of the container. To modal, the sloshing problems, (i) flow is considered irrotational, (ii) small displacement of the free surface of the liquid is considered. We introduce a cartesian coordinate system $(x,y,z)$ in which $z$ is measured vertical upwards from the mean position of the surface. The origin $O$ is regarded at the mean surface and $z=-h$ represents the bottom of the container. Figure $1$ depicts the schematics diagram.

Fig. 1Schematic diagram of the problem

Linear water wave theory is used to formulate the problem. Under these assumptions, fluid flow inside the fluid domain can be described in terms of velocity potential $\mathrm{\Phi }$ from the following governing equation:

which is Laplace equations in cartesian coordinates where:

To investigate the responses of fluid, this Laplace equation must be solved subject to the boundary conditions. Since the tank is rigid, boundary conditions are given at the sidewalls and bottom. Boundary Conditions at the sidewall will be:

Boundary condition at the bottom will be:

A rigid baffle of width $\alpha a$ is placed on the free surface of the liquid which divides the free surface condition into two conditions. Free surface conditions for the given problem are as follows:

where $g$ is the gravitational constant. In order to solve the above boundary value problem, assume:

The analytical solution for Eq. (1) subjected to boundary conditions Eq. (2)-(24) is obtained by using method of separation of variables which is given by:

Now, the analytical solution given by Eq. (7) is used in the free surface conditions given by Eq. (5)-(6) to obtain following homogenous systems:

Eqs. (8-9) represent homogenous system of algebraic equations in the integration constants $A_{mn}$. For the non-trivial solution of this system, the determinant of the coefficient matrix must be zero which gives the sloshing frequencies.

3. Numerical results

The first mode of liquid-free surface and sloshing frequencies are reported using ANSYS software for numerical simulation. In the presented paper, tank length, width and filling level is considered $b=\mathrm{}$2 m, $a=\mathrm{}$1 m and $h=\mathrm{}$1 m respectively and baffle width is taken $\alpha =\mathrm{}$0.3 m.

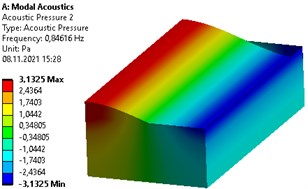
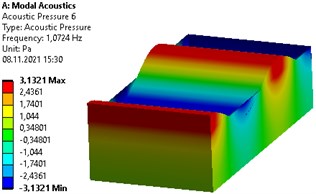
Firstly, the case no baffle at the free surface of the liquid is considered. Frequencies corresponding to first four modes is presented in Table 1 for three dimensional rectangular container with dimensions $b=$ 2 m, $a=$ 1 m and $h=$ 1 m respectively. One can see that the lowest frequency is observed corresponding to the first mode. The highest frequency is reported to correspond to the fourth mode.

The modes of first axisymmetric vibrations for $b=\mathrm{}$2 m, $a=\mathrm{}$1 m and $h=\mathrm{}$1 m respectively in un-baffled container are shown in Fig. 2. These are the pressure contours which shows the sloshing in three dimensional rectangular tank.

Fig. 2First modes of liquid vibrations in un-baffled rectangular container

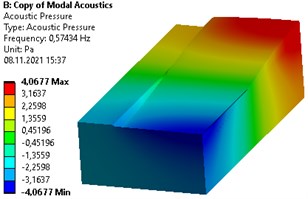
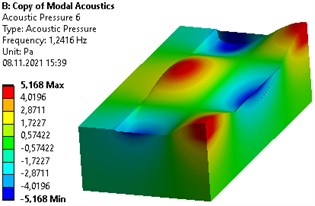
Secondly, a rigid baffle is placed at the free surface of the liquid towards left side of the container. Numerical simulation is done with dimensions $b=$ 2 m, $a=$ 1 m and $h=$ 1 m respectively. Baffle width is considered $\alpha =$ 0.3 m. Fig. 3 shows the first mode of liquid vibrations for baffled container.

Fig. 3First modes of liquid vibrations in baffled rectangular container

Frequencies of axisymmetric modes for the various value of $h$ is presented in Table 2. One can see that the frequencies value are increasing for the higher value of the filling level of the liquid. Highest frequency value is reported corresponding to $h=$ 0.5 m.

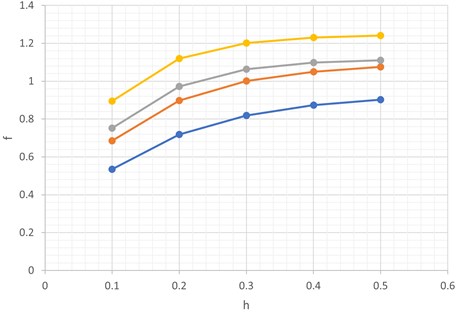
Fig. 4 and Fig. 5 shows the dependency of frequencies versus filling level $h$ for different values of $h$. These curves are drawn for different values of baffle width $\alpha =$ 0 and $\alpha =$ 0.3 m respectively. It can be seen that frequency increases with increasing value of filling level $h$. The effect of baffle width is also shown. It is observed that the frequency value is higher in the case of a baffle placed at the free surface of the liquid.

Fig. 4Frequencies versus filling level for = 0 m

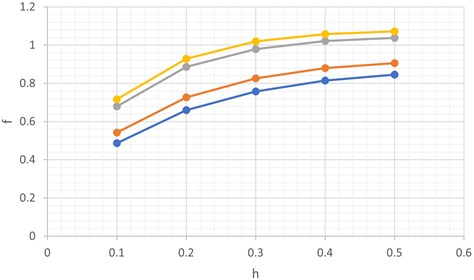
Fig. 5Frequencies versus filling level for = 0.3 m

4. Conclusions

In the presented paper, a rigid three-dimensional rectangular container partially filled with an incompressible and inviscid fluid is considered. The effect of a rigid baffle placed on the free surface of the liquid towards the left side of the container is analyzed. The sloshing modes of the container with and without baffle are reported. Sloshing frequencies for different value of filling level $h$ is presented. The findings showed sloshing frequencies dependent on baffle width and filling level of the liquid. It is noticed that sloshing frequencies are increasing in case of baffle placed at the free surface of the liquid, resulting in reduced sloshing.