Abstract
Concrete rectangular liquid storage structure (CRLSS) with a large height-width ratio has good application prospects due to saving land resources. 3-D Solid element and 3-D Fluid element are used to simulate structure and liquid; and free surface is set to simulate the liquid sloshing behavior. Based on potential flow theory, a three-dimensional numerical model for CRLSS with large height-width ratio is established by ADINA. Results show that wall tensile stress exceeds the concrete tensile strength 2.39 MPa when liquid level height reaches to 11.70 m. There are the optimal baffle positions which can ensure that the wall tensile stress is less than the concrete tensile strength when PGA is 0.22 g, and the wall tensile stress reaches the minimum value when the baffle height is 3.6 m. Opening size has little effect on the wall tensile stress, but it has a significant effect on the baffle tensile stress. Seismic capacity of CRLSS with large height-width ratio designed by using the optimal baffle position can meet the requirements when PGA is 0.22 g, and it is necessary to carry out further comprehensive damping measures when PGA reaches 0.62 g. The arrangement of horizontal baffle can provide an effective way for the engineering application of large height-width ratio CRLSS.
Highlights
- A three-dimensional numerical model of concrete rectangular liquid storage structure with large height-width ratio is established.
- Adding horizontal baffle is effective for the design and application of concrete rectangular liquid storage structure with height-width ratio by adding horizontal baffle.
- Effect of horizontal baffle height position on the mechanical behavior of concrete rectangular liquid storage structure with height-width ratio is investigated.
1. Introduction
Earthquake will not only cause damage to the liquid storage structure itself, but also cause secondary disasters such as environmental pollution and fire due to the leakage of some special liquid. The most serious consequence is that people’s life safety is threatened, and there are many cases of damage to the liquid storage structure in all previous earthquakes. The frequency of earthquakes increases in the global scope in recent years, and liquid storage structure is developing towards the direction of large-scale and quantization at the same time, in addition liquid types are increasing day by day, which makes the probability and threat of damage of liquid storage structure under the action of earthquakes greater. Most of the traditional CRLSSs are low structures and this type of structure will cause the waste of land resources due to its large area, so its application will be limited with the development of the city and the shortage of land resources. It is necessary to study the CRLSS with large height-width ratio to save land resources. The mechanical behavior of concrete structure under earthquake is complex, the finite element method is widely used in the study of seismic dynamic response of concrete structures [1-7].
Liquid storage structure is in a very complex state of stress under the action of earthquake, and researchers have carried out a lot of research on this kind of structure. Mandal and Maity [8] conducted a nonlinear hydrodynamic analysis of elastic water tank, and found that distribution of nonlinear hydrodynamic pressure was almost similar to the linear pressure due to ground excitation. Musil and Sivý [9] conducted seismic analysis of circular vertical ground-supported tanks and investigated influence of wall flexibility on hydrodynamic pressures. Khanmohammadi et al. [10] used a series of small-scale experimental tests to investigate the effect of amplitude and frequency of input excitation on responses of concrete rectangular liquid storage tanks. Kormaníková et al. [11] pointed out that pressures and forces acting onto walls and bottom and total hydrodynamic effects under earthquake played fundamental role in the design of liquid on storage tank. Moradi et al. [12] proposed a mechanical model is for evaluating the seismic response of flexible concrete cylindrical tanks under horizontal ground motion. Meng et al. [13] concluded that soil-structure interaction had no apparent effect on the convective frequency and liquid surface wave elevation. Hejazi and Mohammadi [14] investigated liquid sloshing response in partially filled rectangular tanks subjected to earthquake ground motions, and obtained that liquid pressure acting on tank under vertical earthquake could be increased, but its effect on sloshing wave height was negligible. Moslemi et al. [15] investigated effects of important parameters on nonlinear sloshing response of rectangular concrete tanks under seismic excitation, and found that sloshing nonlinearity had a significant effect on seismic performance of liquid containing structures.
As an effective measure to reduce liquid sloshing wave height and liquid pressure, separator has been widely studied. Feng et al. [16] found that the existence of baffles could mitigate sloshing effects and the mitigation performance depended on the shape, structure and location of the baffles. Wang et al. [17] investigated floating circular, wall-mounted ring and floating ring baffles or with inclination for liquid storage tank under laterally-excited action. Cruchaga et al. [18] found that major reduction of the wave height was obtained when larger baffles were positioned closer to the water level at rest. Hosseini et al. [19] proposed a novel sloshing reduction technique by using suspended annular baffle to reduce seismic sloshing of liquid storage tanks. Chu et al. [20] investigated sloshing phenomenon in a rectangular water tank with multiple bottom-mounted baffles, and obtained that sloshing height and hydrodynamic force decrease as baffle height increase. Hajimehrabi et al. [21] evaluated effects of baffle on the seismic behavior of concrete cylindrical tanks. Cheng et al. [22] proposed CRLSS with vertical baffle simplified calculation method. Zang et al. [23] studied effects of the porous baffle length, porosity and design on the sloshing force, wave surface elevation, and velocity field.
Liquid storage structure is in a very complex stress state under earthquake action because of fluid-solid interaction, and a large number of researches on CRLSS are carried out for the small height-width ratio at present. CRLSS with large height-width ratio has a good application prospect because of its large liquid storage capacity and saving land resources, but the research on this kind of structure is very limited. The particularity of this kind of structure lies in that with the increase of height-width ratio and liquid level height, the structure is easy to be damaged due to large liquid pressure. Considering the fluid-solid interaction and sloshing behavior of liquid free surface, a three-dimensional numerical model of CRLSS with large height-width ratio is established based on finite element method and potential flow theory. Variation law of structural response after adding horizontal baffle is investigated, influence law of baffle position, opening size, PGA and seismic action direction on dynamic responses is analyzed. The research results can provide reference for the design and engineering application of CRLSS with large height-width ratio.
2. Solution of fluid-structure interaction
Dynamic equation of the structure under earthquake action can be expressed as [24]:
where , and are the mass, damping and stiffness matrices of the structure, respectively; is the displacement vector; is the earthquake acceleration vector; is the liquid pressure vector; is the force vector equivalent to the element stresses.
Dynamic equation of liquid can be obtained from the fluid dynamics theory based on the liquid sloshing theory as follows:
where is the liquid density; is the input excitation vector transferred to the liquid by the structure; , , and are coefficient matrices, and the specific expressions are as follows:
where is the shape function.
The fluid-solid coupling equation of the liquid storage structure can be expressed as:
The incremental dynamic finite element equilibrium equation of the structure can be expressed as:
The following dynamic control equations can be obtained through the iterative calculation of equilibrium:
where is the matrix between strain and displacement; is the stress; represents the volume.
The incremental dynamic finite element equilibrium equation of the liquid can be expressed as:
The damping in the dynamic equation adopts Rayleigh damping model:
3. Numerical calculation model
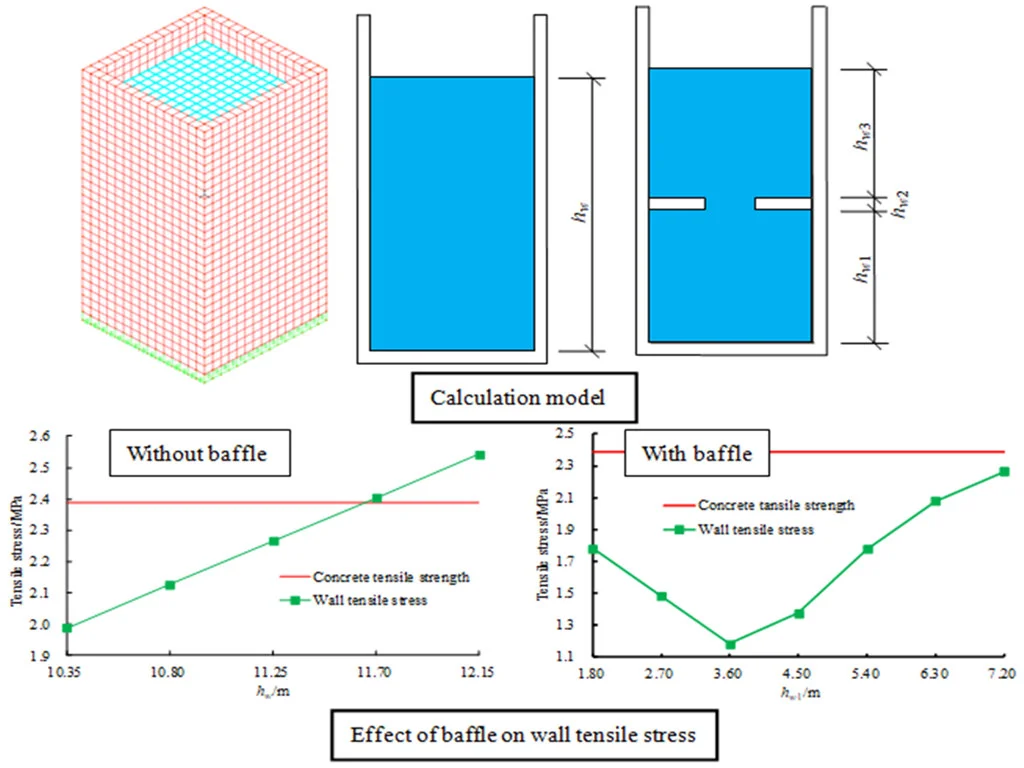
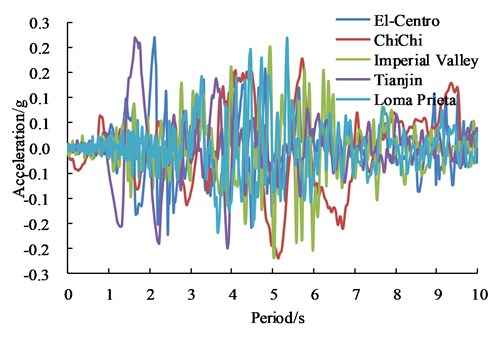
The size of CRLSS is 6.75 m×6.75 m×13.5 m, the height-width ratio and the wall thickness are 2 and 0.45 m, respectively. Concrete strength grade is C40, its elastic modulus is 3.25×1010Pa, Poisson's ratio is 0.20, density is 2500 kg/m3, and structure is simulated by 3-D Solid element. The liquid was modeled by potential fluid with density of 1000 kg/m3 and volume modulus of 2.3×109 Pa. The 3-D Fluid element was used to simulate the fluid. The free surface boundary is set to simulate the sloshing behavior of the liquid, and the structure and the liquid contact position are set to establish the boundary conditions of the fluid-solid interaction. Five seismic waves including El-Centro, ChiChi, Imperial Valley, Tianjin and Loma Prieta are selected for time-history analysis. Time-history curves of acceleration and response spectrum are shown in Fig. 1. The three-dimensional numerical calculation model of CRLSS established by ADINA is shown in Fig. 2 [25-27].
Fig. 1Seismic waves
4. Key technology of engineering application
With the increase of liquid level height, pressure acting on the wall of CRLSS with large height-width ratio increases, which leads to the bottleneck problem in the application of traditional CRLSS with large height-width ratio (Fig. 3). In order to solve the wall cracking caused by excessive hydraulic pressure, the horizontal baffle is arranged along the height of the liquid storage structure, and opening holes are set on the horizontal baffle to connect the upper and the lower spaces, which is convenient for normal use and later maintenance, as shown in Fig. 4. The baffle position parameters adopt 7 kinds of design schemes, as shown in Table 1. Firstly, the variation law of wall tensile stress under hydrostatic pressure of traditional rectangular concrete liquid storage structure with large height-width ratio is discussed, as shown in Fig. 5.
Fig. 2Calculation model

Fig. 3Liquid storage structure with large height-width ratio
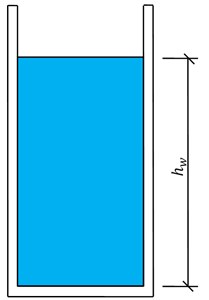
Fig. 4Schematic baffle of design position of horizontal baffle
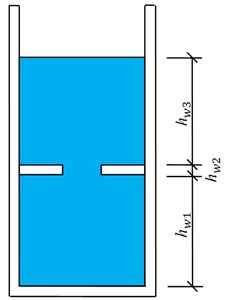
Table 1Design scheme of baffle positions
Schemes | Parameters | ||
/ m | / m | / m | |
1 | 1.80 | 0.45 | 9.45 |
2 | 2.70 | 0.45 | 8.55 |
3 | 3.60 | 0.45 | 7.65 |
4 | 4.50 | 0.45 | 6.75 |
5 | 5.40 | 0.45 | 5.85 |
6 | 6.30 | 0.45 | 4.95 |
7 | 7.20 | 0.45 | 4.05 |
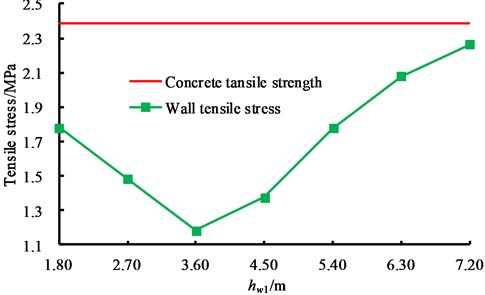
According to Fig. 5, due to the influence of liquid pressure, the wall tensile stress increases with the increase of the liquid level height. The wall tensile stress exceeds the concrete tensile strength 2.39 MPa when liquid level height reaches to 11.70 m. This indicates that the engineering application of CRLSS with large height-width ratio will be limited, so it is of great significance to develop the key technology for CRLSS with large height-width ratio.
As 11.70 m, 3.60 m, 0.45 m and 7.65 m (11.70 m), calculation results of the stress of CRLSS with large height-width ratio without baffle and with baffle are shown in Figs. 6 and 7, and the influence rule of baffle position on the tensile stress of the wall under the seven design schemes is shown in Fig. 7.
Fig. 5Variation law of wall tension stress with the liquid level height
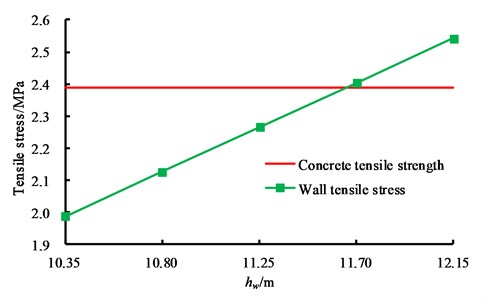
Fig. 6Stress of wall parallel to X-axis
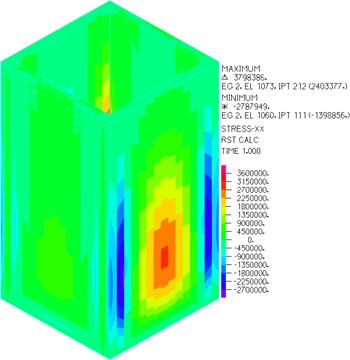
a) Without baffle
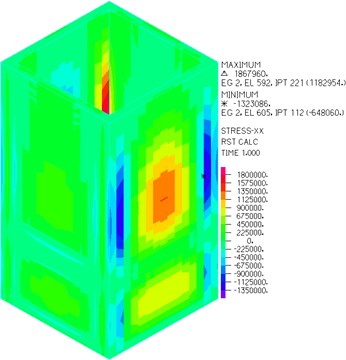
b) With baffle
Fig. 7Stress of wall parallel to Y-axis
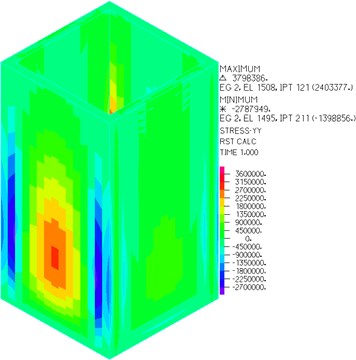
a) Without baffle
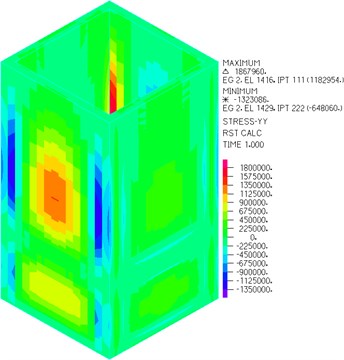
b) With baffle
As can be seen from Figs. 6-8, the wall tensile stress is significantly reduced after arranging horizontal baffle with hole, and the wall tensile stress is less than the concrete tensile strength when seven kinds of baffle positions are arranged for the CRLSS with large height-width ratio. Besides, setting baffle can change the stress distribution significantly.
With the increase of baffle height, the wall tensile stress firstly decreases and then increases. When 3.6 m, the wall tensile stress reaches the minimum value of 1.183 MPa, which is far less than the tensile strength of concrete 2.39 MPa. The wall thickness of concrete liquid storage structure with large height-width ratio can be further reduced by reasonable baffle arrangement, thus saving materials.
Fig. 8Influence law of baffle position on tensile stress of wall panel
5. Dynamic responses analysis under earthquakes
In order to consider the system damping, Lanczos iterative method was first used for modal analysis. The first and second order modes and frequencies of the structure and the liquid when 3.60 m, 0.45 m and 7.65 m are shown in Figs. 9 and 10. The results of the first and second order frequencies of the structure and liquid corresponding to 7 kinds of baffle designs are shown in Table 2.
Fig. 9Structure modes and frequencies

a) First-order freqency (18.43)

b) Second-order freqency (18.43)
In order to further investigate baffle effects on the mechanical behavior law of CRLSS with large height-width ratio, dynamic responses of CRLSS with large height-width ratio under earthquake is studied after the static analysis. The calculation results of the wall tensile stress under the 7 kinds of baffle setting schemes are shown in Fig. 11.
Table 2Frequencies of structure and liquid under 7 types of baffle arrangement
/ m | Structure | Liquid | ||
/ Hz | / Hz | / Hz | / Hz | |
1.8 | 18.61 | 18.61 | 0.3660 | 0.4358 |
2.7 | 18.58 | 18.58 | 0.3660 | 0.4358 |
3.6 | 18.54 | 18.54 | 0.3659 | 0.4358 |
4.5 | 18.49 | 18.49 | 0.3658 | 0.4358 |
5.4 | 18.43 | 18.43 | 0.3654 | 0.4357 |
6.3 | 18.35 | 18.35 | 0.3645 | 0.4356 |
7.2 | 18.25 | 18.25 | 0.3620 | 0.4349 |
Fig. 10Liquid modes and frequencies

a) First-order freqency (.3659)

b) Second-order freqency (0.4358)
Fig. 11Influence law of baffle position on tensile stress of wall panel
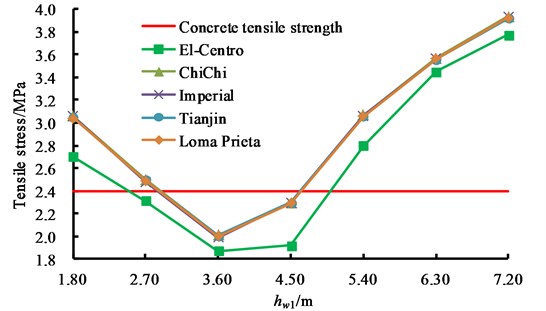
As can be shown from Fig. 11, with the increase of baffle height position, the wall tensile stress firstly decreases and then increases under the action of five seismic waves. The tensile stress reaches the minimum value when 3.6 m, namely, the effect of baffle height position on the tensile stress of CRLSS with large height-width ratio is very significant. The wall tensile stress does not exceed the concrete tensile strength when 3.6 m and 4.5 m, the wall tensile stress does not exceed the concrete tensile strength only under the action of El-Centro wave when 2.7 m, and the wall tensile stresses under the action of five seismic waves all exceed the concrete tensile strength when 5.4 m, 6.3 m and 7.2 m. It is helpful to improve the seismic capacity of CRLSS when the horizontal baffle closes to the lower part of the structure.
The results show that the location of horizontal baffle is a very important design parameter to ensure the safety of CRLSS with large height-width ratio in seismic fortification area under earthquake action. The optimal design can be achieved by adjusting the baffle height location.
6. Analysis of influencing factors
6.1. Baffle opening size
The opening size is one of the important design parameters of the horizontal baffle of the CRLSS with large height-width ratio. A variety of opening sizes are selected to calculate and analyze the wall tensile stress under the action of five seismic waves. The specific results are shown in Tables 3 and 4. Under El-Centro wave, distributions of baffle tensile stress with different opening sizes are shown in Fig. 12.
Table 3Wall tensile stress under different opening sizes / MPa
Seismic waves | Opening sizes | |||
1.35 m×1.35 m | 2.25 m×2.25 m | 3.15 m×3.15 m | 4.05 m×4.05 m | |
El-Centro | 1.858 | 1.868 | 1.925 | 2.035 |
ChiChi | 2.010 | 2.006 | 2.083 | 2.043 |
Imperial Valley | 2.002 | 1.986 | 2.081 | 2.041 |
Tianjin | 2.010 | 2.002 | 2.075 | 2.035 |
Loma Prieta | 2.001 | 1.997 | 2.069 | 2.029 |
Table 4Horizontal baffle tensile stress of under different opening sizes / MPa
Seismic waves | Opening sizes | |||
1.35 m×1.35 m | 2.25 m×2.25 m | 3.15 m×3.15 m | 4.05 m×4.05 m | |
El-Centro | 1.335 | 1.535 | 2.126 | 3.337 |
ChiChi | 1.491 | 1.747 | 2.380 | 3.350 |
Imperial Valley | 1.493 | 1.746 | 2.378 | 3.352 |
Tianjin | 1.488 | 1.470 | 2.371 | 3.332 |
Loma Prieta | 1.488 | 1.735 | 2.367 | 3.329 |
According to Table 3, the wall tensile stress increases with the increase of the opening size under the action of El-Centro seismic wave, however, the wall tensile stress fluctuates with the increase of the opening size and the change range of the tensile stress on the whole is small under the action of ChiChi, Imperial Valley, Tianjin and Loma Prieta seismic waves.
According to Table 4, under action of five seismic waves, horizontal baffle tensile stresses are increased with the increase of the opening size. When the opening size increases to 3.15 m × 3.15 m, horizontal baffle tensile stress will exceed concrete tensile strength and wall crack will be caused. It is further shown from the Fig. 12 that the opening size also has a great influence on the distribution of baffle stress.
Although the opening size has little effect on the wall tensile stress, it has a significant effect on the distribution of baffle stress. Therefore, in order to ensure the safety of large height-width ratio CRLSS, opening size is an important parameter of baffle design, for example, it is better when opening sizes are 1.35 m×1.35 m and 2.25 m×2.25 m in this paper.
6.2. Earthquake direction and PGA
The PGA of 5 seismic waves is adjusted to 0.22 g, 0.40 g and 0.62 g, respectively, and the calculation results of the wall tensile stress under the seismic action of , ( 1:0.85) and ( 1:0.85:0.62) direction are shown in Table 5, in which the axis is the main axis.
Fig. 12Tensile stress distribution of horizontal baffle under El Centro wave
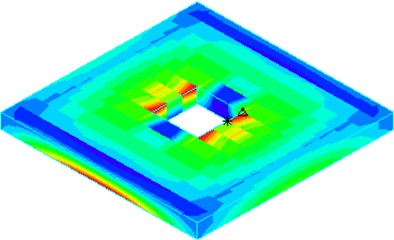
a) 1.35 m×1.35 m
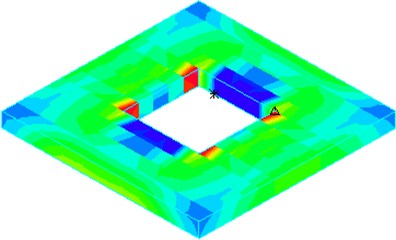
b) 2.25 m×2.25 m
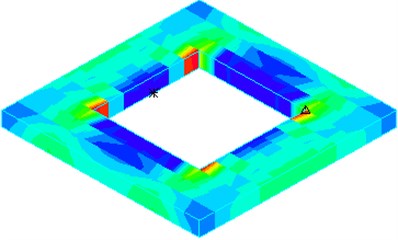
c) 3.15 m×3.15 m
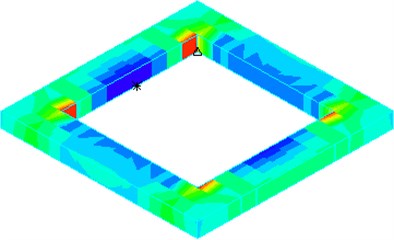
d) 4.05 m×4.05 m
Table 5Influence of PGA on wall tensile stress
Seismic waves | Directions | PGA/g | ||
0.22g | 0.40g | 0.62g | ||
El-Centro | 1.858 | 1.876 | 2.039 | |
1.874 | 2.081 | 2.595 | ||
1.896 | 2.487 | 3.223 | ||
ChiChi | 2.010 | 2.022 | 2.042 | |
2.018 | 2.045 | 2.227 | ||
2.037 | 2.425 | 3.139 | ||
Imperial Valley | 2.002 | 1.986 | 2.224 | |
1.986 | 2.278 | 2.899 | ||
2.133 | 2.925 | 3.903 | ||
Tianjin | 2.010 | 2.015 | 2.031 | |
2.012 | 2.033 | 2.159 | ||
1.996 | 2.097 | 2.600 | ||
Loma Prieta | 1.997 | 2.006 | 2.364 | |
2.004 | 2.422 | 3.135 | ||
2.154 | 3.156 | 4.261 | ||
According to Table 5, in most cases, the wall tensile stress under the action of unidirectional, bidirectional and three-dimensional seismic waves is less than the tensile strength of the concrete 2.39 MPa when PGA is 0.22 g, and the maximum tensile stress is 2.154 MPa under three-dimensional Loma Prieta earthquake. The wall tensile stress under unidirectional earthquake is less than the tensile strength of the concrete when PGA is increased to 0.40 g and 0.62 g, while the wall tensile stress in most cases exceeds the tensile strength of concrete under three-dimensional seismic waves.
The influence of multi-dimensional earthquake on the wall tensile stress is small when PGA is 0.22 g, while the influence of multi-dimensional earthquake on the wall tensile stress is significant when the PGA is 0.40 g and 0.62 g, and the influence of vertical earthquake on the wall tensile stress is more significant.
In general, for the large height-width ratio CRLSS with horizontal baffle, its seismic capacity can meet the requirements when PGA is 0.22 g, it has certain seismic capacity when PGA is 0.40 g, and its seismic capacity cannot meet the requirements in most cases when PGA is 0.62 g. Therefore, it is necessary to investigate the comprehensive vibration control measures for large height-width ratio CRLSS under some rare earthquakes.
7. Conclusions
Aiming at the CRLSS with large height-width ratio, arranging horizontal baffle is put forward to solve the bottleneck problem, a three-dimensional numerical calculation model is established, effectiveness of this measure is investigated, and parameter analysis is also carried out. The main conclusions are as follows:
1) The wall tensile stress will exceed the concrete tensile strength when the liquid level height increases to a large value, which limits the engineering application of CRLSS with large height-width ratio.
2) When a horizontal baffle is installed, the wall tensile stress under static force will not exceed the concrete tensile strength, the wall tensile stress under earthquake first decreases and then increases with the increase of the horizontal baffle height, the wall tensile stress reaches the minimum value when 3.6 m. Therefore, there is an optimal design for the horizontal baffle location of the large height-width ratio CRLSS.
3) The influence of the opening size of the horizontal baffle on the tensile stress of the large height-width ratio CRLSS is small, while the influence of the opening size on the tensile stress of horizontal baffle is very significantly. When the opening size is increased to 2.25 m×2.25 m, tensile stress of horizontal baffle exceeds concrete tensile strength 2.39 MPa.
4) In most cases, the seismic capacity of large height-width ratio CRLSS with horizontal baffle can meet the requirements when the PGA = 0.22 g. With the increase of PGA, the probability of tensile stress exceeding the concrete tensile strength increases, and the probability of the wall tensile stress exceeding the concrete tensile strength under the multi-dimensional earthquake is very large especially when the PGA is 0.62 g.
References
-
Shishegaran A., Khalili M. R., Karami B., Rabczuk T., Shishegaran A. Computational predictions for estimating the maximum deflection of reinforced concrete panels subjected to the blast load. International Journal of Impact Engineering, Vol. 139, 2020, p. 10352.
-
Shishegaran, Aydin, Mohammad Reza Ghasemi, Hesam Varaee Performance of a novel bent-up bars system not interacting with concrete. Frontiers of Structural and Civil Engineering, Vol. 13, Issue 6, 2019, p. 1301-1315.
-
Shishegaran Aydin, et al. Developing conductive concrete containing wire rope and steel powder wastes for route deicing. Construction and Building Materials, Vol. 232, 2020, p. 117184.
-
Reza Ghasemi M., Shishegaran A. Role of slanted reinforcement on bending capacity SS beams. Vibroengineering Procedia, Vol. 11, 2017, p. 195-199.
-
Fahiminia M., Shishegaran A. Evaluation of a developed bypass viscous damper performance. Frontiers of Structural and Civil Engineering, Vol. 14, 2020, p. 773-791.
-
Shishegaran A., Amiri A., Jafari M. A. Seismic performance of box-plate, box-plate with UNP, box-plate with L-plate and ordinary rigid beam-to-column moment connections. Journal of Vibroengineering, Vol. 20, Issue 3, 2018, p. 1470-1487.
-
Shishegaran A., Rahimi S., Darabi H. Introducing box-plate beam-to-column moment connections. Vibroengineering Procedia, Vol. 11, 2017, p. 200-204.
-
Mandal K. K., Maity D. Nonlinear finite element analysis of elastic water storage tanks. Engineering Structures, Vol. 99, 2015, p. 666-676.
-
Musil M., Sivý M. Influence of wall flexibility of liquid storage tanks on hydrodynamic pressures induced during seismic activity. 22nd International Conference Engineering Mechanics, 2016.
-
Khanmohammadi M., Rad P. L., Ghalandarzadeh A. Experimental study on dynamic behavior of buried concrete rectangular liquid storage tanks using shaking table. Bulletin of Earthquake Engineering, Vol. 15, Issue 9, 2017, p. 3747-3776.
-
Kormaníková E., Kotrasová K. Multiscale modeling of liquid storage laminated composite cylindrical tank under seismic load. Composites Part B: Engineering, Vol. 146, 2018, p. 189-197.
-
Moradi R., Behnamfar F., Hashemi S. Mechanical model for cylindrical flexible concrete tanks undergoing lateral excitation. Soil Dynamics and Earthquake Engineering, Vol. 106, 2018, p. 148-162.
-
Meng X., Li X., Xu X., et al. Earthquake response of cylindrical storage tanks on an elastic soil. Journal of Vibration Engineering and Technologies, Vol. 7, 2019, p. 433-444.
-
Hejazi F. S. A., Mohammadi M. K. Investigation on sloshing response of water rectangular tanks under horizontal and vertical near fault seismic excitations. Soil Dynamics and Earthquake Engineering, Vol. 116, 2019, p. 637-653.
-
Moslemi M., Farzin A., Kianoush M. R. Nonlinear sloshing response of liquid-filled rectangular concrete tanks under seismic excitation. Engineering Structures, Vol. 188, 2019, p. 564-577.
-
Feng Y. T., Li X., Tan Y., et al. A comparative study of different baffles on mitigating liquid sloshing in a rectangular tank due to a horizontal excitation. Engineering Computations, 2015.
-
Wang W., Peng Y., Zhou Y., et al. Liquid sloshing in partly-filled laterally-excited cylindrical tanks equipped with multi baffles Applied Ocean Research, Vol. 59, 2016, p. 543-563.
-
Cruchaga M. A., Ferrada C., Márquez N., et al. Modeling the sloshing problem in a rectangular tank with submerged incomplete baffles. International Journal of Numerical Methods for Heat and Fluid Flow, Vol. 26, Issues 3-4, 2016, p. 722-744.
-
Hosseini M., Goudarzi M. A., Soroor A. Reduction of seismic sloshing in floating roof liquid storage tanks by using a suspended annular baffle (SAB). Journal of Fluids and Structures, Vol. 71, 2017, p. 40-55.
-
Chu C. R., Wu Y. R., Wu T. R., et al. Slosh-induced hydrodynamic force in a water tank with multiple baffles. Ocean Engineering, Vol. 167, 2018, p. 282-292.
-
Hajimehrabi H., Behnamfar F., Samani A. K., et al. Fragility curves for baffled concrete cylindrical liquid-storage tanks. Soil Dynamics and Earthquake Engineering, Vol. 119, 2019, p. 187-195.
-
Cheng X. S., Jing W., Gong L. J. Liquid sloshing problem in a concrete rectangular LSS with a vertical baffle. Arabian Journal for Science and Engineering, Vol. 44, Issue 5, 2019, p. 4245-4256.
-
Zang Q., Fang H., Liu J., et al. Boundary element model for investigation of the effects of various porous baffles on liquid sloshing in the two dimensional rectangular tank. Engineering Analysis with Boundary Elements, Vol. 108, 2019, p. 484-500.
-
Qi Y. C., Qiu H. X., Ma Y. Q. Experimental study and finite element analysis on the sloshing suppression in storage tank under seismic excitations. Journal of Vibration and Shock, Vol. 36, Issue 2, 2017, p. 190-195.
-
Cheng X. S., Jing W., Gong L. J. Simplified model and energy dissipation characteristics of a rectangular liquid-storage structure controlled with sliding base isolation and displacement-limiting devices. Journal of Performance of Constructed Facilities, Vol. 31, Issue 5, 2017, https://doi.org/10.1061/(ASCE)CF.1943-5509.0001066.
-
Cheng X. S., Jing W., Du Y. F., et al. Study on shock mitigation of concrete rectangular liquid storage structure with sliding shock insulator and limiting devices based on shaking table test. China Civil Engineering Journal, Vol. 51, Issue 12, 2018, p. 120-132.
-
Cheng X. S., Jing W., Li G. L., et al. Dynamic response of a rectangular liquid-storage structure considering foundation effect under small amplitude sloshing. Journal of Vibration and Shock, Vol. 36, Issue 7, 2017, p. 164-170.
About this article
This paper is a part of the National Natural Science Foundation of China (Grant number: 51908267; 51708270), a part of the Ningxia Center for Research on Earthquake Protection and Disaster Mitigation in Civil Engineering (2020AAC02007), a part of the Hongliu Outstanding Young Talents Support Program of Lanzhou University of Technology (04-061807) a part of the Gansu Youth Science and Technology Fund Program (20JR5RA433), and a part of the Key scientific and technological projects in Gansu Province (JK2019-13).
