Optimization of natural frequency for hexachiral structure based on response surface method

Chen, Luyun; Yi, Hong

doi:10.21595/jve.2020.21350

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 November 2020

Check for updates

Optimization of natural frequency for hexachiral structure based on response surface method

Luyun Chen¹

Hong Yi²

^{1, 2}State Key Laboratory of Ocean Engineering, MOE Key Lab Marine Intelligent Equipment and System, Shanghai Jiao Tong University, Shanghai, 200240, P. R. China

Corresponding Author:

Luyun Chen

Cite the article Download PDF

Downloads 1059

CrossRef Citations 2

Abstract

To improve the resistance to vibration and reduce its structure mass, the structural dynamic properties of hexachiral structure with negative Poisson’s ratio (NPR) are investigated. The optimization function of natural frequencies parameters is established, in which the thickness of circular nodes wall and ligaments of the hexachiral structure are defined as design variable. By normalizing the weight coefficients corresponding to the natural frequencies of different orders, the multi-objective optimization problem is converted into a single objective structural optimization problem. Finally, the cell of hexachiral structure for example, by introducing the response surfaces method, the structural optimization is carried out. The numerical analysis shows that the natural frequency is greatly increased, and the vibration resistance is strengthened. The results provide technical support for the design and application of high performance materials.

Optimization of natural frequency for hexachiral structure based on response surface method

Highlights

The multi-objective optimization problem is converted by introducing the weight coefficients.
The response surface method (RSM) is adopt.
The mechanical properties of hexachiral structure is improved by structural optimization.

1. Introduction

With the development of science and technology, the structural vibration and noise reduction problem have recently been the focus of considerable attention, in which involved development and application of high performance materials. Due to the high specific strength, significant light weight, high specific energy, high specific stiffness and designable, the excellent mechanical properties of honeycomb structure have become the current research hotspot, and it is widely used in shipbuilding, aerospace, automotive engineering, and so on. For the honeycombs cellular materials, there exist kinds of negative Poisson’s ratio (NPR) [1]. Evidently, the artificial materials with negative Poisson’s ratio are constructed from conventional materials, leading to the appearance of microscopic positive Poisson's ratio and macroscopic negative Poisson’s ratio structures. The negative Poisson’s ratio structures including reentrant hexagonal honeycombs, chiral honeycomb structure, rotating unit structures, hollow sphere, and so on [2]. Among them, the chiral honeycomb structure is composed of circular node structure and surrounding ligaments. The described basic unit can either be constructed right-handed or left-handed, creating chiral or anti-chiral structures. Because of these geometrical features of chiral honeycomb structure, this may result in a negative Poisson's ratio close to –1 in-plane mechanical isotropy. Since the number of ligaments attached to each circular node should be equal to the order n of rotational symmetry, there exist five chiral honeycomb structures: trichirals and anti-trichirals, tetrachirals and anti-tetrachirals, and hexachirals [3, 4]. In recent years, the mechanical properties of shear resistance, indentation resistance, high energy absorption, co-curvature and special deformation characteristics of the hexachiral structure have attracted many scholars' attention [5-7], and hexachiral structure has been widely used in impact resistant structures and vibration and noise reduction structures [8, 9]. In the present work, only hexachiral honeycomb structures are concerned.

The mechanical properties of microscopic material affect the macroscopic mechanical properties of the hexachiral structure. The spatial topological parameters of the hexachiral structure, such as the connection factor between edges and surfaces, the number of adjacent holes and the angle between them, will directly affect the mechanical properties of the hexachiral structure [10-12]. The mechanical properties of hexachiral structure is mainly determined by topology type of cell, ligament length and thickness, circular node radius and thickness in macroscopic [13-16]. Discussing the macroscopic stiffness and modal parameters of the cell structure are the primary method to study the mechanical properties of NPR structure. In order to improve the mechanical performance of negative Poisson's ratio structure, the parameters such as microscopic material, ligament length and thickness, circular node radius and thickness can be optimized. Structural natural frequency is the inherent dynamic parameter of the elastic structure, and it is sensitive to alterations in structural stiffness and mass matrices. As an important index to evaluate structural resistance, optimizing the structural natural frequency is effective [17, 18].

The main objective of present work is to investigate the structural dynamic properties of the hexachiral structures. In order to improve the stiffness of the hexachiral structure, the response surface method (RSM) is adopt to study the relationship between natural frequencies parameters and design variable, in which the natural frequencies parameters are defined as objective function. The remainder of the present article is organized as follows: in Section 2, some basic concepts and mechanics function of hexachiral structure are presented; in Section 3, the structural optimization problem based on natural frequency is discussed; in Section 4, the response surface method are introduced; in Section 5, a cell of hexachiral structure for example, the feasibility and effectiveness of the proposed method is illustrated by numerical analysis; finally, the conclusion was drawn in Section 6.

2. Hexachiral structure

2.1. Concept of hexachiral structure

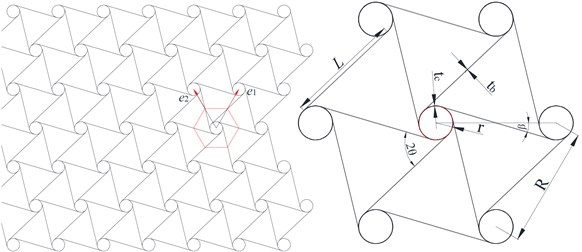
The basic cells of hexachiral structure are formed by connecting straight ligaments to the central circular nodes. The cell of hexachiral structure consists of a circular node and ligaments tangentially connected to it, each ligament is connected to and tangent to another circular node. The main geometric parameters in the hexachiral structure include ligament length $L$ , the distance between circular node centers $R$ , circular node radius $r$ , circular node wall thickness $t_{c}$ and ligament thickness $t_{b}$ . The hexagonal chiral honeycomb structure is shown in Fig. 1.

As shown in Fig. 1, the hexachiral structure is composed of multiple cells, the lattice vector $e_{1}$ and $e_{2}$ are used to define the periodicity of the hexachiral structure. The position of each cell in the hexachiral structure can be determined according to the linear combination of the lattice vector $n_{1} e_{1} + n_{2} e_{2}$ . The symmetry vectors is defined as $e_{1}$ and $e_{2}$ , and it can be expressed as:

1

\{\begin{array}{l} e_{1} = [R c o s θ, R s i n θ]^{T} = {[\frac{\sqrt{3} R}{2}, \frac{R}{2}]}^{T}, \\ e_{2} = [- R c o s θ, R s i n θ]^{T} = {[- \frac{\sqrt{3} R}{2}, \frac{R}{2}]}^{T} . \end{array}

The angle between the imaginary line connecting the circular node centers and the ligament is defined as $β$ , the angle between ligaments is denoted as 2 $θ$ , and the geometric relationships can be expressed as follows:

2

s i n β = \frac{2 r}{R}, t a n β = \frac{2 r}{L}, s i n θ = \frac{R / 2}{R}, c o s β = \frac{L}{R} .

Since the geometric property of the hexachiral structure lattice is in-plane hexagonal symmetry, according the Eq. (1), the angle $θ$ is always 30°, and the hexagonal chiral topology is invariant to in-plane rotations by the angle 2 $θ$ , regardless of the topology parameter.

Fig. 1The sketch of hexagonal chiral honeycomb

2.2. The mechanics analysis of cell hexachiral structure

To analyze the dynamic property of the chiral honeycomb structure, studying the mechanical properties of the cell structure is necessary. At first, several hypotheses are defined to establish the motion equation of the hexachiral structure: (1) six ligaments are attached tangentially to each rigid circular node; (2) the application of loading in one direction causes the rotation of circular node which gives rise to auxetic behavior in the transverse direction; (3) Poisson’s ratio close to –1.

When the hexachiral structure is subjected to external force, all of the ligaments are extruded to produce bending deformation, and the circular node is twisted under the action of each ligaments. Fig. 2 shows the deformations of the circular nodes and ligament (dotted line).

Fig. 2Schematic diagram of thin beam bending of ligament

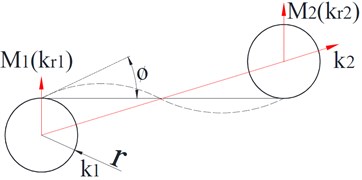
As shown in Fig. 2, it is assumed that the circular nodes and ligaments deform within the elastic range. The main deformation of the ligaments is bending, and the thin and long ligament is simplified as an Euler beam. The main deformation of circular node is torsioning, and the circular nodes is regarded as a torsional spring. The cell of hexachiral structure can be simplified as an Euler beam elastically connected with the circular node at both ends. Based on the above hypothesis, the bending vibration equation of the ligament can be written as follows:

3

E I \frac{\partial^{4} y}{\partial x^{4}} + m \frac{\partial^{2} y}{\partial t^{2}} = 0,

where, $E I$ is the bending stiffness of ligament section, $m$ is the mass per unit length of ligament. According to the Euler-Bernoulli beams theory, the vibration mode functions of the ligament beams can be obtained by separating variables:

4

y (x) = c_{1} s i n λ x + c_{2} c o s λ x + c_{3} s h λ x + c_{4} λ x,

where $c_{1}$ ~ $c_{4}$ are the integral constant, $λ = m ω^{2} / 4 E I$ , and $ω$ is the natural circular frequency of the ligament beam.

Assuming the elastic coefficients of the torsional spring and the linear spring corresponding to the circular node at both ends of the cell are the same, i.e. $k_{r 1} = k_{r 2} = k_{r}$ , $k_{1} = k_{2} = k$ , where the elastic coefficients of the torsional spring is $k_{r}$ and the elastic coefficients of the linear spring is $k$ . Based on the boundary condition hypothesis, according the bending vibration equation, the modal equation of the ligament beam can be deduced as follows:

5

{[c o s^{2} (x) - c h^{2} (x) - s i n^{2} (x) + s h^{2} (x)] x^{8} + [- 4 k_{r}^{'} c h (x) s i n (x)] x^{7}

+ [4 k_{r}^{'} s i n (x) s h (x)] x^{6} + [- 2 k^{'} c o s (x) s i n (x) - 2 k^{'} c o s (x) s h (x)] x^{5}

+ [2 k_{r}^{'} k^{'} c o s (x) (c h (x) - c o s (x))] x^{4} + [4 {k_{}^{'}}^{2} s i n (x) s h (x)] x^{2}

+ [2 k_{r}^{'} k'^{2} (c o s (x) s i n (x) + c o s (x) s h (x) - 2 c h (x) s i n (x))] x

+ {k_{r}^{'}}^{2} {k^{'}}^{2} [c o s^{2} (x) - 2 c o s (x) c h (x) + c h^{2} (x) + s i n^{2} (x) - s h^{2} (x)]} / x^{8} = 0,

where $k_{r}^{'} = k_{r} l / E I$ , $k_{}^{'} = k l^{3} / E I$ . Eq. (5) is a transcendental equation. The natural frequencies of the ligament beam structure are related to the design parameters of the circular nodes, ligament and the microscopic material parameter.

3. Frequency-based structural optimization model

If the microscopic material of the hexachiral structure is determined, it is necessary to implement the structural optimization for improving the resistance property of the hexachiral structures. The structural optimizations include topology optimization, shape optimization and sizing optimization. In this study, the sizing optimization is discussed for the hexachiral structure.

3.1. Structural frequency analysis

Since the resistance property of the hexachiral structures are related to the design parameters of circular node and ligament. Natural frequency is an important index to evaluate structural resistance, and it is a important parameter in structural optimization. In the low-middle frequency band, the normalizing formula of structural natural frequency parameters can be written as a non-linear least square method problem:

6

R_{f} (x) = \sum_{i = 1}^{N} w_{i} \frac{f_{i}^{*} (x)}{f_{i}^{0} (x)}, (i = 1,2, \dots, N),

where $R_{f} (x)$ is the normalization value, $N$ is the number of modes of the concerned structure; $f_{i}^{0} (x)$ and $f_{i}^{*} (x)$ denote the $i$ -th natural frequency of the initial design and optimal design, respectively. $w_{i}$ is the weight coefficient to be imposed on different orders of natural frequency, that is, the influence of the natural frequency on the objective function of different orders.

In the practical engineering, the natural frequency vary in orders, corresponds to different weighting coefficient. In order to evaluate the natural frequency parameter of the hexachiral structure, it is necessary to normalize the natural frequency values of different orders. Among them, the weight coefficient $w_{i}$ of each order of modal satisfies the normalization condition [19, 20]. The weight coefficient equation can be obtained by normalizing as follows:

7

\sum_{i = 1}^{N} w_{i} = 1,

where weight coefficient $w_{i}$ satisfies $w_{i} \geq 0$ . The weight coefficients factors for the different order depend on the inherent characteristics of the FE model, the goal of the designer, and so on.

3.2. Multi-objective optimization function

The structural optimization problem can be converted into searching a group of design variables in design scope which maximize the structural stiffness. In the structural optimization of hexachiral structure, the objective is to maximize the structural stiffness of the cell of hexachiral structure under certain mass, that is, maximum natural frequency involves different orders mode. The geometry parameters are defined as design variables, and the structural optimization function based on the maximization of natural frequencies can be written as follows.

Find:

8

X = (x_{1}, x_{2}, \cdot \cdot \cdot, x_{i})^{N}, (i = 1,2, \dots, N) .

Max $R_{f} (x) = \sum_{i = 1}^{N} w_{i} \frac{f_{i}^{*} (x)}{f_{i}^{0} (x)}$ ,

S.t.: $h_{p} (x_{i}) \leq 0$ , $\sum_{i = 1}^{N} w_{i} = 1$ , $x_{i}^{l} \leq x_{i} \leq x_{i}^{u}$ , $(i = 1,2, \dots, N)$ ,

where $X = (x_{1}, x_{2}, \cdot \cdot \cdot, x_{i})^{N}$ is design variables for n dimensions, such as the thickness of ligament or circular node wall; $R_{f} (x)$ is the natural frequency normalization value; $h_{p} (x_{i})$ is constraints condition, such as cell structure mass; $x_{i}^{l}$ and $x_{i}^{u}$ are lower and upper bounds for design variables, respectively.

4. Response surface methodology and experiment design

In this study, in order to search for the globally optimum, response surface method (RSM) is proposed. Response surface method can construct polynomial approximations to functional relationships between design variables and performances, it is a statistical approach based on the experimental design [21, 22]. With the experimental design, the expressed relations between the design variables and objective function will be deduced. By using the results of a numerical experiment in the points of orthogonal experimental design, response surface method is computationally much less expensive than a solution using the original method.

4.1. The response surface model

Generally, the relationship between the response variable of interest $(y)$ and the predictor variables ( $x_{1}$ , $x_{2}$ ,…, $x_{k}$ ) may be known exactly as a description in the following equation:

9

y = f (x_{1}, x_{2}, \cdot \cdot \cdot, x_{k}) + ε,

where ( $x_{1}$ , $x_{2}$ ,…, $x_{k}$ ) are the independent variables, $ε$ is the model error and includes measurement error and other variability. The approximation function is the first-order model can be written as follows:

10

y = β_{0} + β_{1} x_{1} + β_{2} x_{2} + \cdot \cdot \cdot + β_{k} x_{k} + ε,

where $β_{0}$ the constant coefficient, $β_{k}$ the linear effect of the kth factor coefficients and $ε$ is the error observed in the response $y$ . The successful application of RSM relies on the identification of a suitable and precise approximation for ( $x_{1}$ , $x_{2}$ ,…, $x_{k}$ ). A second-order polynomial could be of the type:

11

y = β_{0} + \sum_{i = 1}^{k} ‍ β_{i} x_{i} + \sum_{i = 1}^{k} ‍ β_{i i} x_{i}^{2} + \cdot \cdot \cdot + \sum_{\begin{matrix} i = 1, i < j \end{matrix}}^{k} ‍ β_{i j} x_{i} x_{j} + ε,

where $β_{i i}$ represents the quadratic effect of the $i$ th factor and $β_{i j}$ represents the cross product effect, or interaction effect, between the $i$ th and $j$ th factors.

The common approach in the RSM is to use regression methods based on least square methods. The method of least squares is typically used to estimate the regression coefficient, which is shown in the following equation:

12

\hat{β} = [\begin{array}{l} β_{0} \\ β_{1} \\ ⋮ \\ β_{k} \end{array}] = (x^{T} x)^{- 1} x^{T} y = {[\frac{1}{k} \sum_{j = 1}^{k} y_{j}, \frac{\sum_{j = 1}^{k} x_{1 j} y_{j}}{\sum_{j = 1}^{k} x_{1 j}^{2}}, \dots, \frac{\sum_{j = 1}^{k} x_{n j} y_{j}}{\sum_{j = 1}^{k} x_{n j}^{2}}]}^{T},

where $n$ is the number of objective function and $k$ is the number of variables. The $\hat{β}$ terms comprise the unknown parameter set which can be estimated by collecting experimental system data. The parameter set can be estimated by regression analysis based upon the experimental data.

4.2. Experimental design method

Selecting a limited number of sample points in the design space as much as possible to reflect the characteristics of the design space is referred to as experimental design. The experimental design is to build essential to the approximate model of the process aspect of the design of sample points selected is appropriate to build plays an important role in the subsequent response surface approximation model; it will directly affect the accuracy of the approximate model, so the experimental design of the selection method is particularly important. The uniform Latin square method is used to select the most appropriate sample points.

The natural frequency optimization problem can be described as a response surface by viewing it as an input-output model. As mentioned in Section 4, the variables are defined as $h$ , $t$ , and the values of them are listed in Table 3. In the RSM, these variables are transformed into coded variables that are dimensionless, zero mean and the same standard deviation.

In this paper, the Latin square experimental design using optimization algorithm makes the sampling points distributed as evenly as possible in the design space. Fig. 3 shows the uniform Latin square method designed the rational experimental samples with two factors, in which, there are 11 points sampling in the spatial arrangement.

Fig. 3Uniform Latin square method

5. Numerical analysis

5.1. Model description

To demonstrate the structural optimization process, the cell of hexachiral structure is chosen. In the cell of hexachiral structure, the structures include two circular nodes and one ligament, as shown in Fig. 2. The geometric parameters are defined as following: $L =$ 50 mm, $s =$ 52 mm, $r =$ 4.0 mm, $h =$ 1.0 mm, $t =$ 1.0 mm and the width of hexachiral structure is 10 mm.

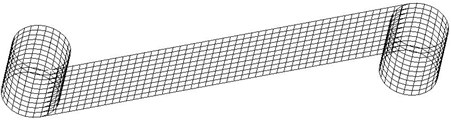
In modal analysis of hexachiral structure, free boundary condition is chosen to reduce the influence of boundary. In present work, all FEM predictions are calculated by using MSC.Patran/Nastran 2012.2, this commercial software is a widely used numerical tool for structural dynamic response analyses. The finite element model of the structure is shown in Fig. 4, which includes 980 quadrilateral elements and 1067 nodes.

The chiral honeycomb structure is made of aluminium alloy with the following mechanical performance: density, $ρ =$ 2700 kg/m³; modulus of elasticity, $E =$ 75 GPa; Poisson ratio, $μ =$ 0.33.

Fig. 4Finite element model of the cell hexachiral structure

5.2. Structural analysis

The natural frequency of the cell of hexachiral structure is obtained through the numerical analysis. The 1-6 orders of the natural frequency of the structure are shown in Table 1.

Table 1Comparison of natural frequency

Modal order	Initial frequency / Hz	Optimized frequency / Hz	natural frequency error / %
1	985.5	1104.4	12.07
2	2159.4	2449.4	13.43
3	2289.8	2576.4	12.52
4	4154.1	4544.6	9.40
5	6397.5	6818.7	6.58
6	7205.9	7762.6	7.72

5.3. Structural optimization

In the structural optimization function, the thickness of circular node wall and the thickness of ligament are defined as design variable, and all of the thickness design variable is discrete variable.

In the structural optimization, the objective function involved are natural frequencies, and the first 6 orders are used for calculation. Considering that the first-order frequency reflects the inherent characteristics of the structure most directly, the weight coefficient value of the fundamental frequency is the largest, whereas the weight coefficients of the other orders are decreasing. The value of the weighting coefficient is shown in Table 2.

Table 2Weight coefficient parameter

Mode order	Weight coefficient
1	0.4
2	0.2
3	0.1
4	0.1
5	0.1
6	0.1

According to response surfaces method, the structural optimization of hexachiral structure based on natural frequency parameter is carried out. The natural frequencies of different orders of the optimized hexachiral structure are obtained, and the mass of the hexachiral structure is 0.00276 kg. The 1-6 orders of the natural frequency of the structure are compared, as shown in Table 3.

Table 3The design variable

Design variables	Initial thickness / m	Optimum thickness / m
Circular nodes wall thickness ( $h$ )	0.001	0.00092
Ligaments thickness ( $t$ )	0.001	0.00108
Total mass / kg	0.00276	0.00275

As shown in Table 3, the natural frequency parameters of the hexachiral structure have been greatly improved by structural optimizing, the natural frequency of the hexachiral structure is increased by 12.07 % while the total mass of the structure is reduced by 0.4 %. The structure performance has been significantly improved, which shows that the proposed method has high effectiveness and good optimization results.

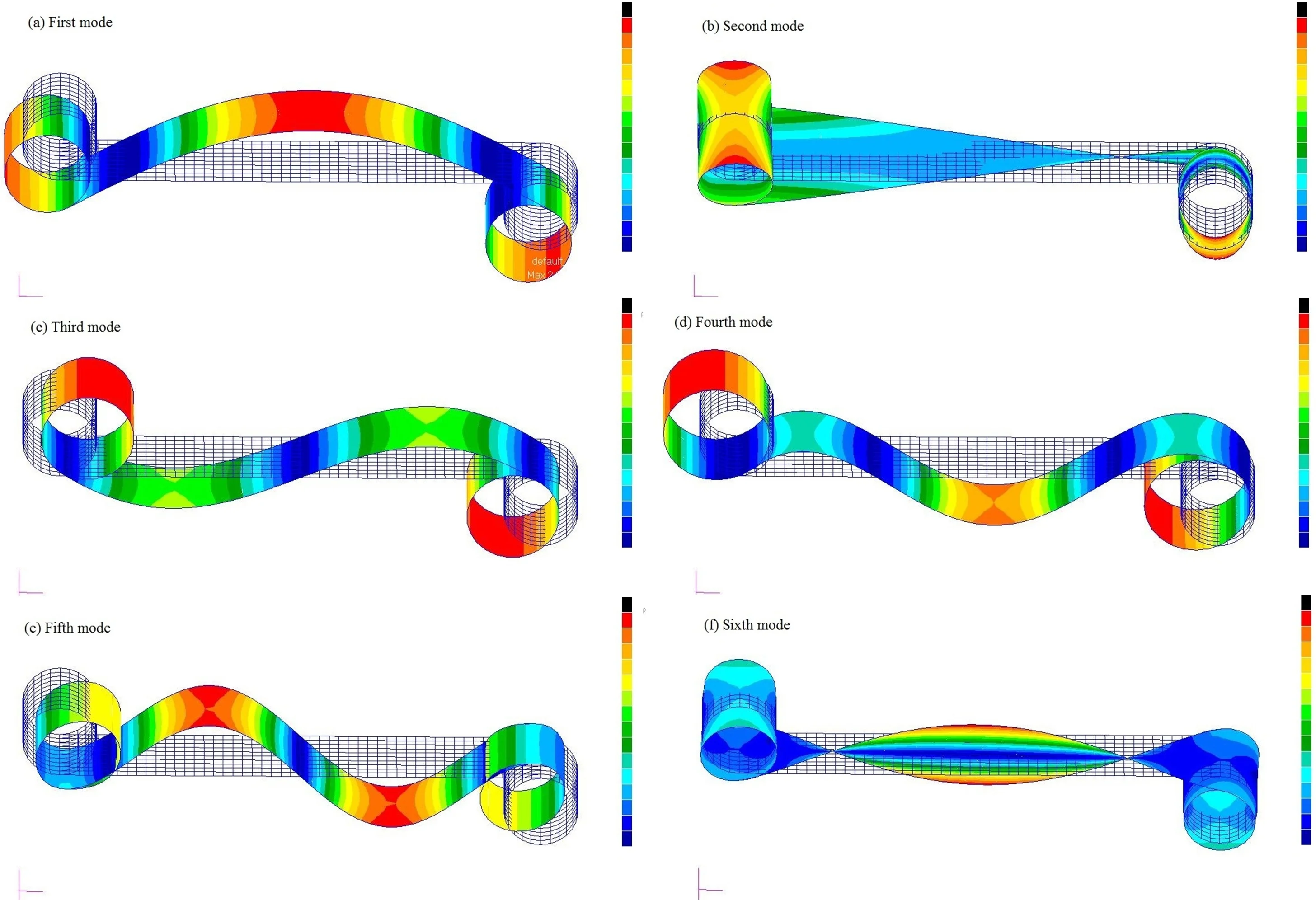
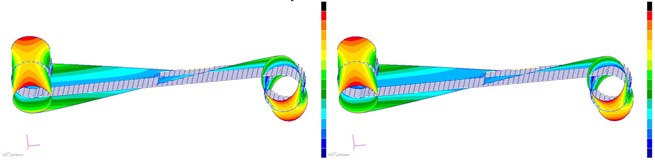
The structural cells mode shapes of first to sixth order are compared, as shown in Fig. 5. The left figures are the mode shapes before optimization, while the right figures are the mode shapes after optimization.

As shown in Fig. 5, comparing the first to sixth order mode shapes before and after optimization, it can be seen that although the elastic coefficients of torsional spring and linear spring decrease with the decrease of the thickness $h$ , the increase of ligament thickness $t$ increases the overall stiffness of structural cells, so it is very important to ensure the ligament strength from the design of the hexachiral structure.

Fig. 5Mode shapes of the cell hexachiral structure

a) First mode

b) Second mode

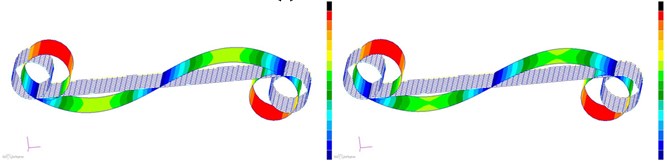
c) Third mode

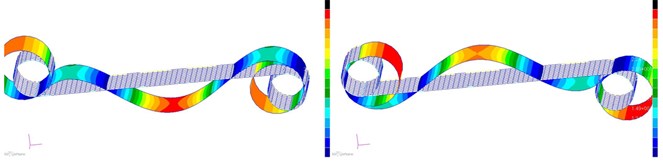
d) Fourth mode

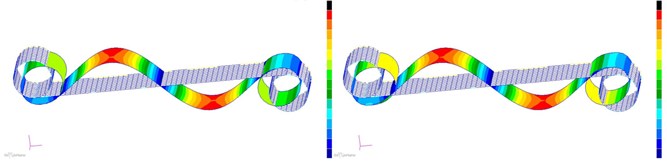
e) Fifth mode

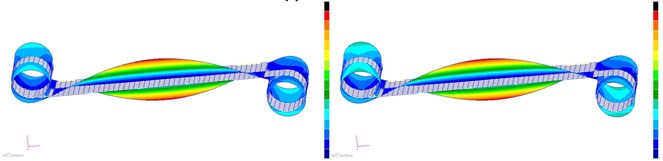
f) Sixth mode

6. Conclusions

In this paper, the vibration equation of the cell of the hexachiral structure is deduced. By defining the natural frequency parameters, the structural optimization equation is established and the structural optimization is carried out. The results show that the structural stiffness can be effectively improved by optimizing the design parameters of the hexachiral structure. The results provide technical support for the design and application of high performance materials for vibration and noise reduction. The numerical analysis shows that the natural frequency is greatly improved and the vibration resistance is strengthened by structural optimization.

References

Saxena K. K., Das R., Calius E. P. Three decades of auxetics research-materials with negative Poisson's ratio: a review. Advanced Engineering Materials, Vol. 18, Issue 11, 2016, p. 1847-1870.

Publisher
Prawoto Y. Seeing auxetic materials from the mechanics point of view: a structural review on the negative Poisson’s ratio. Computational Materials Science, Vol. 58, Issue 1, 2012, p. 140-153.

Publisher
Chen Y. Y., Li T. T., Jia Z. A., et al. 3D printed hierarchical honeycombs with shape integrity under large compressive deformations. Materials and Design, Vol. 137, Issue 1, 2018, p. 226-234.

Publisher
Evans K. E., Alderson A. Auxetic materials: functional materials and structures from lateral thinking. Advance Materials, Vol. 12, Issue 9, 2000, p. 617-628.

Publisher
Collet M., Ouisse M., Ruzzenz M., et al. Floquet-Bloch decomposition for the computation of dispersion of two-dimensional periodic, damped mechanical systems. International Journal of Solids and Structures, Vol. 48, Issue 20, 2011, p. 2837-2848.

Publisher
Grima J. N., Gatt R., Ellul B., et al. Auxetic behaviour in non-crystalline materials having star or triangular shaped perforations. Journal of Non-Crystalline Solids, Vol. 356, Issue 1, 2010, p. 1980-1987.

Publisher
Qin H. X., Yang D. Q., Ren C. H. Modelling theory of functional element design for metamaterials with arbitrary negative Poisson’s ratio. Computational Materials Science, Vol. 150, Issue 33, 2018, p. 121-133.

Publisher
Gao D. W., Zhang C. W. Theoretical and numerical investigation on in-plane impact performance of chiral honeycomb core structure. Journal of Structural Integrity and Maintenance, Vol. 3, Issue 2, 2018, p. 95-105.

Publisher
Bezazi A., Scarpa F. Mechanical behaviour of conventional and negative Poisson's ratio thermoplastic polyurethane foams under compressive cyclic loading. International Journal of Fatigue, Vol. 29, Issue 5, 2007, p. 922-930.

Publisher
Wan H., Ohtaki H., Kotosaka S., et al. A study of negative Poisson’s ratio in auxetic honeycombs based on a large deflection model. European Journal of Mechanics a/Solids, Vol. 23, Issue 1, 2004, p. 95-106.

Publisher
Shufrin I., Pasternak E., Dyskin A. V. Negative Poisson’s ratios in hollow sphere materials. International Journal of Solid and Structures, Vol. 54, Issue 1, 2014, p. 192-214.

Publisher
Zhang X. W., Yang D. Q. Mechanical properties of auxetic cellular material consisting of re-entrant hexagonal honeycombs. Materials, Vol. 9, Issue 900, 2016, p. 900.

Publisher
Spadoni A., Ruzzene M., Gonella S., et al. Phononic properties of hexagonal chiral lattices. Wave Motion, Vol. 46, Issue 7, 2009, p. 435-450.

Publisher
Wang B., Cheng G. D. Design of cellular structures for optimum efficiency of heat dissipation. Structural and Multidisciplinary Optimization, Vol. 30, Issue 6, 2005, p. 447-458.

Publisher
Alderson A., Alderson K. L., Attated D., et al. Elastic constants of 3-, 4- and 6- connected chiral anti-chiral honeycombs subject to uniaxial in-plane loading. Composites Science and Technology, Vol. 70, Issue 7, 2010, p. 1042-1048.

Publisher
Zhu Y. L., Wang Z. P., Poh L. H. Auxetic hexachiral structures with wavy ligaments for large elasto-plastic deformation. Smart Materials and Structures, Vol. 27, Issue 5, 2018, p. 055001.

Publisher
Liu X. N., Huang G. L., Hu G. K. Chiral effect in plane isotropic micropolar elasticity and its application to chiral lattices. Journal of the Mechanics and Physics of Solids, Vol. 60, Issue 2, 2012, p. 1907-1921.

Publisher
Ebrahimi H., Mousanezhad D., Nayeb Hashemi H. 3D cellular metamaterials with planar anti-chiral topology. Materials and Design, Vol. 145, Issue 2, 2018, p. 226-231.

Publisher
Yang I. T., Wang W. C., Yang T. I. Automatic repair of inconsistent pairwise weighting matrices in analytic hierarchy process. Automation in Construction, Vol. 22, 2012, p. 290-297.

Publisher
Li H. Z., Guo S. External economies evaluation of wind power engineering project based on analytic hierarchy process and matter-element extension model. Mathematical Problems in Engineering, Vol. 2013, Issue 1, 2013, p. 848901.

Publisher
Shokuhfar A., Khalili S. M. R., Ghasemi F. A., et al. Analysis and optimization of smart hybrid composite plates subjected to low-velocity impact using the response surface methodology (RSM). Thin-Walled Structures, Vol. 46, Issue 1, 2008, p. 1204-1212.

Publisher
Xu Y. M., Shuo S. L., Rong X. M. Composite structural optimization by Genetic Algorithm and neural network response surface modeling. Chinese Journal of Aeronatics, Vol. 18, Issue 4, 2005, p. 310-316.

Publisher

Cited by

Dynamic Behavior of Soft and Hard Materials, Volume 3

Rukmangad S. Barad | Akshay Pathania | B. K. Nagesh | S. Anand Kumar

(2024)

Finite Element Analysis and Machine Learning in the Loop Additive Manufacturing Process Parameter Optimization to Acquire the Desired Dynamics of Manufactured Parts

Can Barış Toprak | Can Ulas Dogruer

(2024)

About this article

Received

23 February 2020

Accepted

15 June 2020

Published

15 November 2020

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/jve.2020.21350

Keywords

hexachiral structure

negative Poisson’s ratio (NPR)

natural frequency

structural optimization

response surface method

Acknowledgements

This study is partially supported by the State Key Laboratory of Ocean Engineering. Such support is gratefully acknowledged by the authors.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 10 30

Mechanical characteristics of a corset type structure with negative Poisson’s ratio

Yuchao Song, Yanxin Yang, Changkuan Chi, Guobin Li, Jiahui Zhang, Zhaowen Zhang

Research article

2023 06 25

Modern development of metamaterials for obtaining special electromagnetic, acoustic, mechanical and vibration-isolating properties

Anvar Valeev, Alexey Zotov, Aliia Siraeva

Research article

2020 05 07

Dynamic response of auxetic structures

Matthieu Proffit, John Kennedy

Research article

2019 11 28

Natural frequency analysis of a functionally graded rotor system using three-dimensional finite element method

Arnab Bose, Prabhakar Sathujoda

L. Chen and H. Yi, “Optimization of natural frequency for hexachiral structure based on response surface method,” Journal of Vibroengineering, Vol. 22, No. 7, pp. 1705–1714, Nov. 2020, https://doi.org/10.21595/jve.2020.21350

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2020.21350
UR  - https://doi.org/10.21595/jve.2020.21350
TI  - Optimization of natural frequency for hexachiral structure based on response surface method
T2  - Journal of Vibroengineering
AU  - Chen, Luyun
AU  - Yi, Hong
PY  - 2020
DA  - 2020/11/15
PB  - JVE International Ltd.
SP  - 1705-1714
IS  - 7
VL  - 22
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Chen_2020,
	doi = {10.21595/jve.2020.21350},
	url = {https://doi.org/10.21595/jve.2020.21350},
	year = 2020,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	number = {7},
	pages = {1705--1714},
	author = {Luyun Chen and Hong Yi},
	title = {Optimization of natural frequency for hexachiral structure based on response surface method},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]L. Chen and H. Yi, “Optimization of natural frequency for hexachiral structure based on response surface method,” Journal of Vibroengineering, vol. 22, no. 7, pp. 1705–1714, Nov. 2020, doi: 10.21595/jve.2020.21350.

Copy IEEE

Copied to clipboard!

Chen, Luyun, and Hong Yi. “Optimization of Natural Frequency for Hexachiral Structure Based on Response Surface Method.” Journal of Vibroengineering 22, no. 7 (November 15, 2020): 1705–14. https://doi.org/10.21595/jve.2020.21350.

Copy Chicago

Copied to clipboard!

Optimization of natural frequency for hexachiral structure based on response surface method

Abstract

Highlights

1. Introduction

2. Hexachiral structure

2.1. Concept of hexachiral structure

2.2. The mechanics analysis of cell hexachiral structure

3. Frequency-based structural optimization model

3.1. Structural frequency analysis

3.2. Multi-objective optimization function

4. Response surface methodology and experiment design

4.1. The response surface model

4.2. Experimental design method

5. Numerical analysis

5.1. Model description

5.2. Structural analysis

5.3. Structural optimization

6. Conclusions

References

Cited by

About this article

Related Articles