Abstract
The article presents the history of the development of metamaterials, which begins with the development of metamaterials to obtain unique electromagnetic properties. The first ideas of such materials appeared in the XIX century. Such constructions make it possible to obtain a negative permittivity, and further the “invisibility effect”. The idea of creating a material with a given microstructure also makes it possible to obtain metamaterials with a negative Poisson’s ratio, acoustic metamaterials. Separately, it should be noted that such an approach makes it possible to obtain metamaterials with negative rigidity and vibration-isolating metamaterials. The article presents the author's design of a vibration-isolating metamaterial with quasi-zero stiffness. A demonstration prototype was made.
1. Introduction
Metamaterial is a structure with a special internal structure that gives it unique properties that are not found in nature. For example, materials with a negative Poisson's ratio do not exist in nature, but thanks to metamaterials this becomes technically possible [1]. In general, metamaterials make it possible to obtain unique properties in various fields, and at the moment they are being actively developed in acoustics, optics, electromagnetism, and a number of other areas. Sometimes metamaterials are also referred to as “smart materials”. The area of application of metamaterials is constantly expanding, approaches are being developed to create the structure of metamaterials, materials with desired properties are being synthesized, and new promising areas of their application are opening up.
Modern advances in the field of additive technologies open up great opportunities in the field of creating metamaterials. In particular, this approach can be used to create special elastic structures in elastic structures, in other words, to manufacture new means of protection against vibration and shock. Synthesizing various internal structures of elastic metamaterials, it is possible to give them different power characteristics, including nonlinear ones.
Due to 3D additive technology and the use of the concept of metamaterials with quasi-zero stiffness, it is possible to create shock protection and vibration isolation systems that can be very thin and compact in their geometric parameters. One layer of such a material can be several millimeters thick, and the ability to create metamaterials with different layers allows you to create layered structures with a set of special properties (such as “sandwich”).
2. The beginning of the development of metamaterials. Metamaterials for obtaining unique electromagnetic properties
The history of metamaterials dates back to the end of the 19th century. The first area of their use was the control of electromagnetic waves, but their active research began only after the Second World War. And further, great prospects for using the optimal range for waves were confirmed.
At the end of the 19th century, scientific works on the control of electromagnetic waves were presented. Thus, a toolkit was proposed in the face of a dielectric lens, a pyramidal electromagnetic horn, a resonator emitter, a microwave absorber, waveguides of various shapes (circle, square and rectangle). In 1887, J. C. Bose developed the concept of microwave optics [1], [2].
The first attempt to investigate “artificial materials”, now metamaterials, can be traced back to 1898, when in 1898 D. C. Bose conducted the first microwave experiment on twisted geometries, which, in fact, were artificial chiral elements in modern terminology [1]. He also investigated the double refraction of waves in crystals. It is worth noting that in the future, these works formed the basis of a new scientific direction, called “stereochemistry”, when in 1915 Pasteur L. more deeply investigated chiral molecules.
In 1904, a number of publications in the field of wave research were published, where the possibility of obtaining a negative phase velocity accompanied by an antiparallel group velocity was discussed, in particular, by G. Lamb and A. Shustrom [3]. In 1905 H. K. Pocklington continued to investigate the effects associated with the negative group velocity of electromagnetic waves [4].
In 1914, Lindman worked on “artificial” chiral media by embedding many randomly oriented small wire helices into a carrier medium [5]. In 1920-1922 Lindman K. F. studied the propagation of microwaves in wire spirals at the macrolevel [6].
After a significant break, in 1945 L. Mandelstam carried out research in the field of the antiparallel phase and the group propagation of electromagnetic waves.
In 1948, V. E. Kok [7] fabricated light microwave lenses by periodically placing conducting elements in the form of a sphere, disks, and stripes. This made it possible to change the effective refractive index and stimulated the study of artificial materials with a complex structure.
In the years that followed, various scientists experimented with different sizes, shapes, and compositions of the inclusions. Various combinations allow you to create a huge variety of different versions of metamaterials with different properties.
Much attention in the study of metamaterials was given to obtaining a negative permittivity. In 1959, VE Pafomov discovered the effect of negative permittivity in the study of crystals and excitons [8]. The results obtained were subsequently confirmed by the research group of V. M. Agranovich and V.L. Ginzburg in 1959 [9].
In 1967 V.G. Veselago theoretically studied the propagation of a plane wave in a material whose permittivity and permittivity were assumed to be simultaneously negative [10]. His theoretical study showed that for a monochromatic homogeneous plane wave in such a medium, the direction of the Poynting vector is opposite to the direction of the phase velocity, in contrast to the case of plane wave propagation in ordinary simple media.
Fig. 1The structure of the first experimental left (“left handed material") of a material with antiparallel behavior of the wave vector and other electromagnetic fields
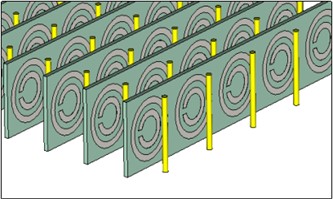
V. G. Veselago also predicted a number of electromagnetic phenomena that are the opposite of traditional ones, in particular introduced the concept of a material with a negative refractive index (Fig. 1). Also, this outstanding scientist is credited with the invention of the term “left material” (“left handed material”). In 1968, an article by V. G. Veselago on materials with a negative refractive index was presented in English [10].
It is noteworthy that V. G. Veselago back in the 1960s. Based on a medium with a negative refractive index, he predicted the ability of light to flow around objects, that is, the ability to hide objects from the field of view, in other words, to create an “invisibility cap”.
It should be noted that during the activities of V. G. Veselago did not yet have the ability to create such materials, and it was only in the 1990s that technologies became available to artificially create the necessary structures.
In continuation of the scientific works of V.G. Veselago in 2000 by D. R. Smith and S. Schultz designed a composite and demonstrated the presence of anomalous refraction in this medium [11], [12]. Several names and terminologies have been proposed for metamaterials with negative permittivity, such as “left media” [11-16]; media with a negative refractive index [10-13], [15]; “backward wave media” (BW media); “doubly negative” metamaterials. Many research groups around the world are currently studying various aspects of this class of metamaterials, and several ideas and suggestions have been put forward for future applications of these materials.
Fig. 2Scheme of the operation of media with a negative refractive index – this is how a glass would look if water had a negative refractive index

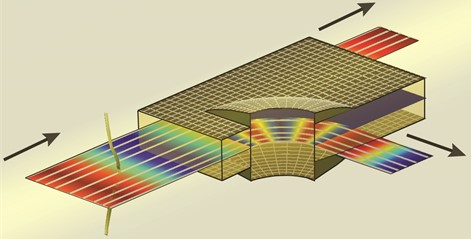
Below is one example of a metamaterial with special optical properties – a light bender. In it, light propagates over the surface of the optical chip and enters the metamaterial layer on the left. Due to a certain change in thickness, the light either deflects to the right or can propagate directly to the output of the optical chip without distortion or refraction (Fig. 3).
Fig. 3Optical metamaterial, directing the flow of light in one of two directions
3. Metamaterials with negative Poisson’s ratio
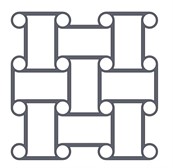
At the end of the 20th century, much attention began to be paid to the concept of “mechanical metamaterials” [17]. Mechanical metamaterials are materials for which macroscale properties are determined by a small-scale topological construction [18]. Rational design of the microarchitecture of these materials results in unusual or unique combinations of mechanical properties that are rarely found in nature. Some of these exceptional mechanical properties include a negative Poisson's ratio or a combination of low stiffness and high strength [19], [20]. Recent developments seen in additive manufacturing (3D printing) have accelerated the production of mechanical metamaterials, facilitating precise control over their microarchitecture (Fig. 4).
One of the first synthetic auxetics was described in 1987 in an article entitled “Foam structures with a Negative Poisson's Ratio” (“Porous structures with a negative Poisson’s ratio”) [21].
In 1990, Evans K., in relation to the latter category, suggested using the term “auxetic metamaterials”. Auxetic metamaterials have received much attention [22], [23], [24], including several special reviews [19], [25].
Fig. 4Examples of the fundamental structure of a metamaterial with a negative Poisson’s ratio

4. Acoustic metamaterials
Acoustic metamaterials are aimed at obtaining unique properties in the field of changes or absorption of sound waves. These metamaterials originate from theoretical studies and discoveries made by V. G. Veselago in 1967.
In the 1990s, D. Pendry created the basic elements of acoustic metamaterials.
In the 2000s, a demonstration of the concept of acoustic metamaterials by means of sonic crystals in a liquid was presented [26]. Further, these studies were expanded, to implement the required properties a resonator with a split ring was used [11].
After that, in 2004, double negative parameters were obtained (negative modulus of elasticity and negative effective density) [27].
Then, in 2009, J. Thomas, L. Yin, and N. Fang presented the structures and results of studies of an ultrasonic lens made of a metamaterial for focusing sound at a frequency of 60 kHz [28].
The first industrial experiments on the use of acoustic metamaterials were for aircraft insulation in 2017 [29]. The research was carried out by a joint group of German (Scientific Institute Center of Applied Aeronautical Research) and Canadian scientists (Mecanum Research Center Inc.).
Fig. 5Soundproof metamaterial developed by Nissan

In 2019, Nissan at CES in Las Vegas introduced a sound deadening metamaterial, which effectively absorbs sound vibrations of air with a frequency of 500-1200 Hz - this is the main range of noise generated when a car is moving (Fig. 5).
5. Metamaterials with negative stiffness and vibration isolation metamaterials
Modern achievements in the field of 3D printing open up new possibilities in the creation of metamaterials aimed at obtaining special mechanical properties.
Giving mechanical metamaterials the effect of negative stiffness allows them to obtain unusual properties that are extremely promising for vibration and shock absorption and isolation.
In structures and metamaterials, negative stiffness is usually achieved due to extended or beam elements subjected to both compression and bending [30-32] of linear springs during rotation [33], [34] and a special arrangement of materials [35], [36]. As the displacement or strain increases, the resistance of the system due to the applied force decreases. Bistable elements are also used - they are very promising in the implementation of microstructures.
M. Wangbo [37] in 1998 analyzed the use of pre-compressed and pinned beams and loaded at midpoints to obtain negative stiffness in practice.
Studies of the bistable mechanism for hysteretic properties were studied by G. Puglisi in 2000 and noted two different types of determining behavior: hysteretic and stable softening [38].
Later in 2001, Yu Qiu et al. [39], [40] presented a bistable mechanism based on pre-bent beams that did not use compressive residual stress for its bistability. The use of periodic structures like metamaterials in the field of shock and vibration isolation metamaterials was studied by A. Carrell [41] in the 2000s.
The method of modal buckling superposition was used to find analytical expressions for various force and midpoint displacement ratios. Cazottes et al. [42] continued these studies in 2015 and studied the mechanical design of a bistable curved beam with different force positions.
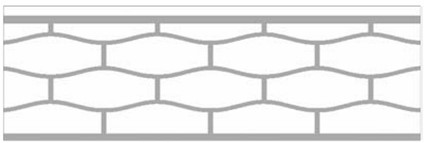
Based on the work of Yu. Qiu, T. Klatt et al. [43] in 2013 presented a recoverable shock-proof cellular structure for absorbing mechanical loads, which was developed by periodically repeating a unit cell of negative stiffness (Fig. 6).
Fig. 6General design of shock absorbing material proposed by Klatt T. in 2013
D. M. Correa et al. [44] fabricated honeycomb structures with negative stiffness using selective laser sintering in 2013 and conducted experimental studies to determine their force characteristics. In the designed structure, rigid central beams were added to prevent horizontal expansion when vertically compressed. A comparison was also made of the energy absorption capacity between the designed structure and the conventional honeycomb structure. These studies were continued by a number of researchers [45], [46], [47].
In 2014, experimental and numerical studies of multidirectional designs of metamaterials with negative stiffness were carried out. B. Florijn et al. [48] presented a model of a soft porous metamaterial with negative stiffness, which was tuned by compressing the material along one of the axes.
Various spatial metamaterials that have negative stiffness in one direction were also introduced in 2015-2016: Rafsanjani et al. [49], Restrepo et al. [50], Frenzel et al. [51], and Shan et al. [52]. All these metamaterials have high impact-resistant properties.
K. Che et al. in 2015 [53] used small changes in unit cell geometry to obtain a deterministic deformation sequence for a unidirectional metamaterial (Fig. 7). S. Findeisen et al. in 2017 [54] presented a detailed analytical and numerical study of the deformation and energy dissipation of three-dimensional cells for a metamaterial.
Frenzel et al. (2016) [51] presented a metamaterial with negative stiffness, consisting of three-dimensional microlattices with instability only along the vertical axis (Fig. 8).
Known publications about metamaterials for broadband vibration isolation at low frequency by Z. Wang, Q. Zhang, K. Zhang and G. Hu [55].
Goldsberry et al. in 2018 [56] and Nadkarny et al. [57] conducted studies to determine the dynamic response under various loads and studied the propagation of waves in a metamaterial.
Thus, metamaterials represent a modern and promising way to achieve the specified unique properties in various industries. In particular, the use of vibration isolation metamaterials will allow obtaining high protective properties in the condition of small dimensions.
Fig. 7Research by Che K. metamaterial with different properties of cell layers

Fig. 8Metamaterial with three-dimensional microlattice

6. Development of the concept of vibration-isolating and shock-proof metamaterials with quasi-zero stiffness
The author proposes a fundamental design of a vibration-isolating metamaterial with an internal structure that provides quasi-zero stiffness during its compression (Fig. 9).
The proposed vibration the metamaterial consists of two outer elastic layers 1 and 2 (Fig. 9), as well as an inner layer, which is an elastic wave-like structure 3, and the free space around is filled with a softer elastic material 4. Thus, an elastic wave-like structure 3 with an elastic material 4 is a periodic structure in the form of cells. The cell of the panel conditionally consists of the upper supporting wall 5, the wall 6, the lower supporting wall 7 and the elastic material 4, which fills the remaining free space.
As the material of the elastic layers 1, 2 and 3 can be used a material that allows a large elastic deformation, such as rubber, its derivatives, polyurethanes or other polymeric materials. As a filler 4 may be a material with a lower modulus of elasticity compared to the elastic layers 1 and 2, or even gases, in particular, air.
Consider the mechanism of operation of one cell. The inclined wall 6 experiences two types of deformation: bending and compression in the radial direction. The bending deformation of the wall 6 without taking into account the compression deformation has a linear force characteristic. As the cell shrinks, the radial compression of the wall 6 increases. This leads to the fact that it tends to return to its original position, compensating for the deformation due to bending. This circumstance gives the power characteristic of the cell a given nonlinear power characteristic. With greater compression of the cell, the radial compression of the wall 6 reaches its maximum. The dimensions of the cell elements and the elastic properties of the upper vertical support wall 5, wall 6, lower vertical support wall 7, and filler 4 are selected in such a way that quasi-zero stiffness is provided in the working position. The load corresponding to this provision is considered nominal (working).
Fig. 9Principal design of the anti-vibration metamaterial with an internal structure providing quasi-zero stiffness: 1, 2 – elastic layers, 3 – inner layer; 4 – filler; 5 – upper supporting wall of one cell; 6 – inclined wall of one cell; 7 – upper supporting wall of one cell
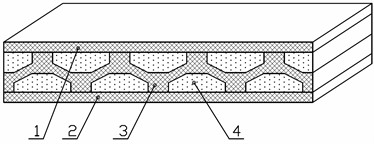
a) General sketch
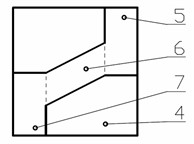
b) Sketch of one cell
The cells form an elastic wave-like structure, which, with such a combination, also has quasi-zero rigidity, providing quasi-zero rigidity to the entire metamaterial.
3D model of a layer of the metmaterial is constructed via Ansys program. A general view of one metamaterial layer is shown in the Figs. 10 and 11.
Fig. 10One layer of metamaterial in an unstressed state
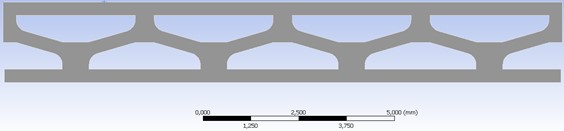
Fig. 11One layer of metamaterial under workload
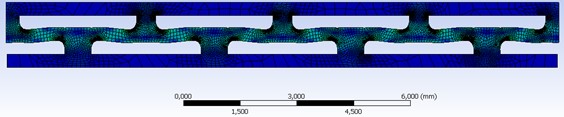
If the metametarial is made of a material with Young’s modulus of 74 MPa, than according 3D modeling the optimal load will already be 14.8 t/m2. The optimal load of half of the cell is 0.3535 N. Based on the geometric parameters, it follows that the optimal load is 19636.4 N/m2 or 2.0 t/m2. The height of one layer in an unstressed state is 1.25 mm. The natural frequency of one layer is 0.81 Hz. With an increase in the number of layers, the frequency of natural oscillations will fall according to a power law of the form x0.5. That is, if there are 10 layers (the thickness of the metamaterial is 1.25 cm), it will be 0.25 Hz, and with 100 layers (the thickness of the metamaterial is 12.5 cm), it will be 0.081 Hz. Force characteristic of one cell of the metamaterial is presented on the Fig. 12.
To test the possibility of manufacturing these metamaterials, demonstration samples were created by printing on a 3D printer PicasoDesigner (Fig. 13). For this, an elastic plastic with a Young’s modulus of 74 MPa was used. The thickness of the layers was 0.3 mm. Each layer was made this slightly different thickness, that means that each layer has different workload.
Fig. 12Force characteristic of one cell of the metamaterial
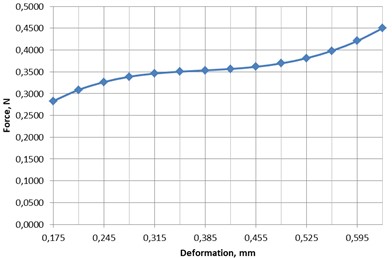
Fig. 13Demonstration samples of anti-vibration metamaterial

Experimental studies have been carried out to determine the force characteristics for samples of developed vibration-proof metamaterials.
Fig. 14Demonstration samples of anti-vibration metamaterial
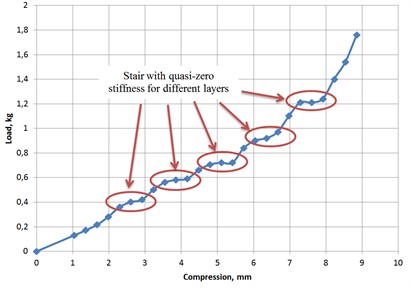
An analysis of the results (Fig. 14) shows that the metamaterial does indeed have zones with quasi-zero stiffness. The force characteristic has different steps, so the quasi-zero stiffness is presented at different loads. The load at each step is approximately 0.15 N.
The use of metamaterials with quasi-zero stiffness will significantly improve the vibration isolation qualities of vibration isolation systems of industrial equipment, in particular oil pumping and gas pumping equipment.
Pumps and compressors are powerful machines that perform responsible work on pumping oil and gas. A high level of vibration can create excessive dynamic loads on equipment, which leads to a decrease in their service life. Maintaining a low vibration background allows maintaining the durability of the equipment, which provides maintain high reliability of energy transport in general.
7. Conclusions
1) Metamaterials is a rapidly developing and promising way to achieve specified unique material properties in various industries. In particular, the use of the concept metamaterials will allow obtaining high vibration isolation properties for industrial equipment.
2) An analysis of the development of vibration protection means has shown, despite the already available theoretical studies of promising highly effective methods for reducing loads on equipment, that their practical application lags behind to a large extent, although there are no technical barriers to their implementation. This is due, in part, to the inertia of the engineering and scientific community in adopting new technologies in practice, and efforts are needed to disseminate and implement them.
3) One of the possible directions for the development of vibration protection systems are vibration isolation metamaterials with quasi-zero stiffness. A feature of these metamaterials is the absence of a direct relationship between their performance parameters and thickness.
4) Due to the absence of a direct relationship between the properties of systems with quasi-zero stiffness and their dimensions, one of the directions for the development of metamaterials with special vibration isolation properties is the use of structures in their cells that provide quasi-zero stiffness.
5) The structure of metamaterials is proposed, which provides quasi-zero stiffness. Demonstration samples of anti-vibration metamaterial are presented. 3D model of a layer of the metamaterial is created. Analysis of the model via Ansys shows that it has a force characteristic with quasi-zero stiffness. It can be very useful for vibration isolation of various types of industrial equipment such as pump, compressors, electric drives, etc.
References
-
D. Li, L. Dong, J. Yin, L. Dong, and R. S. Lakes, “Numerical analysis on mechanical behaviors of hierarchical cellular structures with negative Poisson’s ratio,” Smart Materials and Structures, Vol. 26, pp. 1–7, 2017.
-
D. T. Emerson, “The work of Jagadis Chandra Bose: 100 years of millimeter-wave research,” IEEE Transactions on Microwave Theory and Techniques, Vol. 45, No. 12, p. 2267, 1997.
-
V. I. Slyusar, “Metamaterials on antenna solutions,” in Proceedings of the 7th International Conference on Antenna Theory and Techniques ICATT’09, pp. 19–24, 2009.
-
H. C. Pocklington, “Growth of a Wave-group when the Group-velocity is Negative,” Nature, Vol. 71, No. 1852, pp. 607–608, Apr. 1905, https://doi.org/10.1038/071607b0
-
I. Lindell, A. Sihvola, and J. Kurkijarvi, “Karl F. Lindman: the last Hertzian, and a harbinger of electromagnetic chirality,” IEEE Antennas and Propagation Magazine, Vol. 34, No. 3, pp. 24–30, 1992.
-
D. L. Jaggard, A. R. Mickelson, and C. H. Papas, “On electromagnetic waves in chiral media,” Applied Physics, Vol. 18, No. 2, pp. 211–216, Feb. 1979, https://doi.org/10.1007/bf00934418
-
W. E. Kock, “Metallic delay lenses,” Bell System Technical Journal, Vol. 27, No. 1, pp. 58–82, Jan. 1948, https://doi.org/10.1002/j.1538-7305.1948.tb01331.x
-
T. A. Klar, A. V. Kildishev, V. P. Drachev, and V. Shalaev, “Negative-index metamaterials: going optical,” IEEE Journal of Selected Topics in Quantum Electronics, Vol. 12, No. 6, p. 1106, 2006.
-
M. Marklund, P. K. Shukla, L. Stenflo, and G. Brodin, “Solitons and decoherence in left-handed metamaterials,” Physics Letters A, Vol. 341, No. 1-4, pp. 231–234, Jun. 2005, https://doi.org/10.1016/j.physleta.2005.04.068
-
V. G. Veselago, “The electrodynamics of substances with simultaneously negative values of ∊ and μ,” Soviet Physics Uspekhi, Vol. 10, No. 4, pp. 509–514, Apr. 1968, https://doi.org/10.1070/pu1968v010n04abeh003699
-
D. R. Smith, W. J. Padilla, D. C. Vier, S. C. Nemat-Nasser, and S. Schultz, “Composite medium with simultaneously negative permeability and permittivity,” Physical Review Letters, Vol. 84, No. 18, pp. 4184–4187, May 2000, https://doi.org/10.1103/physrevlett.84.4184
-
R. A. Shelby, D. R. Smith, and S. Schultz, “Experimental verification of a negative index of refraction,” Science, Vol. 292, No. 5514, pp. 77–79, Apr. 2001, https://doi.org/10.1126/science.1058847
-
J. B. Pendry, “Negative refraction makes a perfect lens,” Physical Review Letters, Vol. 85, No. 18, pp. 3966–3969, Oct. 2000, https://doi.org/10.1103/physrevlett.85.3966
-
C. Caloz, C.-C. Chang, and T. Itoh, “Full-wave verification of the fundamental properties of left-handed materials in waveguide configurations,” Journal of Applied Physics, Vol. 90, No. 11, pp. 5483–5486, Dec. 2001, https://doi.org/10.1063/1.1408261
-
A. K. Iyer and G. V. Eleftheriades, “Negative refractive index metamaterials supporting 2-D waves,” in IEEE MTT International Microwave Symposium (IMS) Digest, pp. 1067–1070, Jul. 2002.
-
C. Caloz, H. Okabe, T. Iwai, and T. Itoh, “Transmission line approach of left-handed materials,” in IEEE AP-S International Symposium and USNC/URSI, 2002.
-
A. A. Zadpoor, “Mechanical meta-materials,” Materials Horizons, Vol. 3, No. 5, pp. 371–381, 2016, https://doi.org/10.1039/c6mh00065g
-
Z. G. Nicolaou and A. E. Motter, “Mechanical metamaterials with negative compressibility transitions,” Nature Materials, Vol. 11, No. 7, pp. 608–613, Jul. 2012, https://doi.org/10.1038/nmat3331
-
H. M. A. Kolken and A. A. Zadpoor, “Auxetic mechanical metamaterials,” RSC Advances, Vol. 7, No. 9, pp. 5111–5129, 2017, https://doi.org/10.1039/c6ra27333e
-
F. S. L. Bobbert et al., “Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties,” Acta Biomaterialia, Vol. 53, pp. 572–584, Apr. 2017, https://doi.org/10.1016/j.actbio.2017.02.024
-
R. Lakes, “Foam Structures with a Negative Poisson's Ratio,” Science, Vol. 235, No. 4792, pp. 1038–1040, Feb. 1987, https://doi.org/10.1126/science.235.4792.1038
-
K. Bertoldi, P. M. Reis, S. Willshaw, and T. Mullin, “Negative Poisson’s ratio behavior induced by an elastic instability,” Advanced Materials, Vol. 22, pp. 361–366, 2010.
-
R. Gatt et al., “Hierarchical auxetic mechanical metamaterials,” Scientific Reports, Vol. 5, No. 1, pp. 1–6, Feb. 2015, https://doi.org/10.1038/srep08395
-
J. I. Lipton, R. Maccurdy, Z. Manchester, L. Chin, D. Cellucci, and D. Rus, “Handedness in shearing auxetics creates rigid and compliant structures,” Science, Vol. 360, No. 6389, pp. 632–635, May 2018, https://doi.org/10.1126/science.aar4586
-
W. Yang, Z.-M. Li, W. Shi, B.-H. Xie, and M.-B. Yang, “Review on auxetic materials,” Journal of Materials Science, Vol. 39, No. 10, pp. 3269–3279, May 2004, https://doi.org/10.1023/b:jmsc.0000026928.93231.e0
-
Z. Liu et al., “Locally resonant sonic materials,” Science, Vol. 289, No. 5485, pp. 1734–1736, Sep. 2000, https://doi.org/10.1126/science.289.5485.1734
-
J. Li and C. T. Chan, “Double-negative acoustic metamaterial,” Physical Review E, Vol. 70, No. 5, p. 055602, Nov. 2004, https://doi.org/10.1103/physreve.70.055602
-
J. Thomas, L. Yin, and N. Fang, “Metamaterial brings sound into focus,” Physics, Vol. 102, No. 19, p. 19430, Jun. 2009.
-
“New Acoustic Insulation Metamaterial Technology for Aerospace.” NASA. https://www.nasa.gov/feature/langley/new-acoustic-insulation-metamaterial-technology-for-aerospace (accessed 2017).
-
J. van Eijk and J. F. Dijksman, “Plate spring mechanism with constant negative stiffness,” Mechanism and Machine Theory, Vol. 14, No. 1, pp. 1–9, Jan. 1979, https://doi.org/10.1016/0094-114x(79)90036-3
-
X. Huang, X. Liu, J. Sun, Z. Zhang, and H. Hua, “Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: A theoretical and experimental study,” Journal of Sound and Vibration, Vol. 333, No. 4, pp. 1132–1148, Feb. 2014, https://doi.org/10.1016/j.jsv.2013.10.026
-
I. A. Guell, A. R. Guell, G. Fabian, L. Mcknight, and L. Valdevit, “Origami and 3D printing of positive and negative stiffness structures,” Materials and Design, Vol. 135, pp. 37–50, 2017.
-
F. Liu, S. Theodossiades, D. M. Mcfarland, A. F. Vakakis, and L. A. Bergman, “Tailoring strongly nonlinear negative stiffness,” Journal of Mechanical Design, Vol. 136, No. 2, p. 02450, Feb. 2014, https://doi.org/10.1115/1.4025794
-
D. Xu, Y. Zhang, J. Zhou, and J. Lou, “On the analytical and experimental assessment of the performance of a quasi-zero-stiffness isolator,” Journal of Vibration and Control, Vol. 20, pp. 2314–2325, 2013.
-
K. Bertoldi, “Harnessing instabilities to design tunable architected cellular materials,” Annual Review of Materials Research, Vol. 47, pp. 51–61, 2017.
-
X. Ren, J. Shen, P. Tran, T. D. Ngo, and Y. M. Xie, “Design and characterisation of a tuneable 3D buckling-induced auxetic metamaterial,” Materials and Design, Vol. 139, pp. 336–342, Feb. 2018, https://doi.org/10.1016/j.matdes.2017.11.025
-
M. Vangbo, “An analytical analysis of a compressed bistable buckled beam,” Sensors and Actuators A: Physical, Vol. 69, No. 3, pp. 212–216, Sep. 1998, https://doi.org/10.1016/s0924-4247(98)00097-1
-
G. Puglisi and L. Truskinovsky, “Mechanics of a discrete chain with bi-stable elements,” Journal of the Mechanics and Physics of Solids, Vol. 48, No. 1, pp. 1–27, Jan. 2000, https://doi.org/10.1016/s0022-5096(99)00006-x
-
J. Qiu, J. Lang, and A. Slocum, “A centrally-clamped parallel-beam bistable MEMS mechanism,” Technical Digest. MEMS 2001. 14th IEEE International Conference on Micro Electro Mechanical Systems (Cat. No.01CH37090), pp. 353–356, 2001.
-
Jin Qiu, J. Lang, and A. Slocum, “A curved-beam bistable mechanism,” Journal of Microelectromechanical Systems, Vol. 13, pp. 137–146, 2004.
-
A. Carrella, “Passive vibration isolators with high-static-low-dynamic-stiffness,” Ph.D. thesis, University of Southampton, UK, 2008.
-
P. Cazottes, A. Fernandes, J. Pouget, and M. Hafez, “Bistable buckled beam: modeling of actuating force and experimental validations,” Journal of Mechanical Design, Vol. 131, No. 10, Oct. 2009, https://doi.org/10.1115/1.3179003
-
T. Klatt, M. Haberman, and C. Seepersad, “Design and analysis of a compliant mechanism for a surgical stapler,” in Proceedings of the 24th International Solid Freeform Fabrication Symposium – An Additive Manufacturing Conference, pp. 1010–1022, 2013.
-
D. M. Correa, T. Klatt, S. Cortes, M. Haberman, D. Kovar, and C. Seepersad, “Negative stiffness honeycombs for recoverable shock isolation,” Rapid Prototyping Journal, Vol. 21, No. 2, pp. 193–200, Mar. 2015, https://doi.org/10.1108/rpj-12-2014-0182
-
B. A. Fulcher, D. W. Shahan, M. R. Haberman, C. Conner Seepersad, and P. S. Wilson, “Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems,” Journal of Vibration and Acoustics, Vol. 136, No. 3, Jun. 2014, https://doi.org/10.1115/1.4026888
-
D. Correa, K. Bostwick, P. S. Wilson, M. Haberman, and C. C. Seepersad, “Mechanical impact performance of additively manufactured negative stiffness honeycombs,” in Proceedings of the 26th International Solid Freeform Fabrication Symposium – An Additive Manufacturing Conference, pp. 1422–1433, 2015.
-
D. M. Correa, “Negative stiffness honeycombs for recoverable shock isolation,” Master’s thesis, The University of Texas at Austin, Austin, TX, USA, 2015.
-
B. Florijn, C. Coulais, and M. van Hecke, “Programmable mechanical metamaterials,” Physical Review Letters, Vol. 113, No. 17, p. 175503, Oct. 2014, https://doi.org/10.1103/physrevlett.113.175503
-
A. Rafsanjani, A. Akbarzadeh, and D. Pasini, “Snapping mechanical metamaterials under tension,” Advanced Materials, Vol. 27, pp. 5931–5935, 2015.
-
D. Restrepo, N. D. Mankame, and P. D. Zavattieri, “Phase transforming cellular materials,” Extreme Mechanics Letters, Vol. 4, pp. 52–60, Sep. 2015, https://doi.org/10.1016/j.eml.2015.08.001
-
T. Frenzel, C. Findeisen, M. Kadic, P. Gumbsch, and M. Wegener, “Tailored buckling microlattices as reusable light-weight shock absorbers,” Advanced Materials, Vol. 28, No. 28, pp. 5865–5870, Jul. 2016, https://doi.org/10.1002/adma.201600610
-
S. Shan et al., “Multistable architected materials for trapping elastic strain energy,” Advanced Materials, Vol. 27, No. 29, pp. 4296–4301, Aug. 2015, https://doi.org/10.1002/adma.201501708
-
K. Che, C. Yuan, J. Wu, H. Jerry Qi, and J. Meaud, “Three-dimensional-printed multistable mechanical metamaterials with a deterministic deformation sequence,” Journal of Applied Mechanics, Vol. 84, No. 1, p. 11004, Jan. 2017, https://doi.org/10.1115/1.4034706
-
C. Findeisen, J. Hohe, M. Kadic, and P. Gumbsch, “Characteristics of mechanical metamaterials based on buckling elements,” Journal of the Mechanics and Physics of Solids, Vol. 102, pp. 151–164, May 2017, https://doi.org/10.1016/j.jmps.2017.02.011
-
Z. Wang, Q. Zhang, K. Zhang, and G. Hu, “Tunable digital metamaterial for broadband vibration isolation at low frequency,” Advanced Materials, Vol. 28, pp. 9857–9861, 2016.
-
B. M. Goldsberry and M. R. Haberman, “Negative stiffness honeycombs as tunable elastic metamaterials,” Journal of Applied Physics, Vol. 123, No. 9, p. 091711, Mar. 2018, https://doi.org/10.1063/1.5011400
-
N. Nadkarni, C. Daraio, and D. M. Kochmann, “Dynamics of periodic mechanical structures containing bistable elastic elements: From elastic to solitary wave propagation,” Physical Review E, Vol. 90, No. 2, p. 023204, Aug. 2014, https://doi.org/10.1103/physreve.90.023204
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
