Abstract
The acoustic black hole has the ability to gather and manipulate the flexural wave in the structure, and can be used to achieve vibration suppression of the structure. A group of FEM models for the vibration analysis of the rectangular plate embedded with acoustic black holes were established in this paper. Four monitoring points on the ABH plate were selected to calculate their vibration velocity response in 100 Hz-3 kHz frequency interval. In order to study the effects of acoustic black hole geometric parameters and damping layer geometric parameters on the vibration response of the ABH plate, 15 combinations of different parameters of the maximum ABH diameter, the truncated thickness of the ABH, the power index of the ABH, and the damping layer thickness, the maximum diameter of the damping layer were selected to calculate the vibration velocity response of the four monitoring points. The calculation result can help us understand the effects of acoustic black hole geometric parameters and damping layer geometric parameters on the vibration suppression of rectangular plate.
Highlights
- FEM models for the vibration analysis of the rectangular plate embedded with acoustic black holes were established.
- The effects of acoustic black hole geometric parameters and damping layer geometric parameters on the vibration response of the ABH plate were3 investigated.
- The calculation result can provide data support for subsequent optimal design.
1. Introduction
In recent years, due to the convergence and manipulation of flexural waves in the structure, the acoustic black hole (ABH) has become a new type of vibration and noise reduction technology. The characteristics of the acoustic black hole are that the local thickness of the solid structure gradually decreases in the form of a power index and finally approaches zero, then this region can gather the flexural waves spreading in the structure here, thereby reducing the vibration of other regions of the structure [1]. Different researchers have carried out many researches on the spread of flexural waves, vibration characteristics, and acoustic characteristics of acoustic black hole structures [2]-[4]. The acoustic black hole is becoming an important research direction in the field of sound and vibration, and it is expected to play an important role in the vibration and noise reduction of various mechanical structures in engineering.
The research on vibration reduction applications of the acoustic black hole in different engineering fields mainly includes: Bowyer et al. [5] studied the vibration suppression effect of one-dimensional ABH on engine turbine blades under excitation of mechanical force and airflow through experiments. He et al. designed a new type of box-type acoustic black hole structure for the beam structure of the aircraft wing and studied the vibration reduction effect within the broadband range through the FEM simulation and experiments [6].
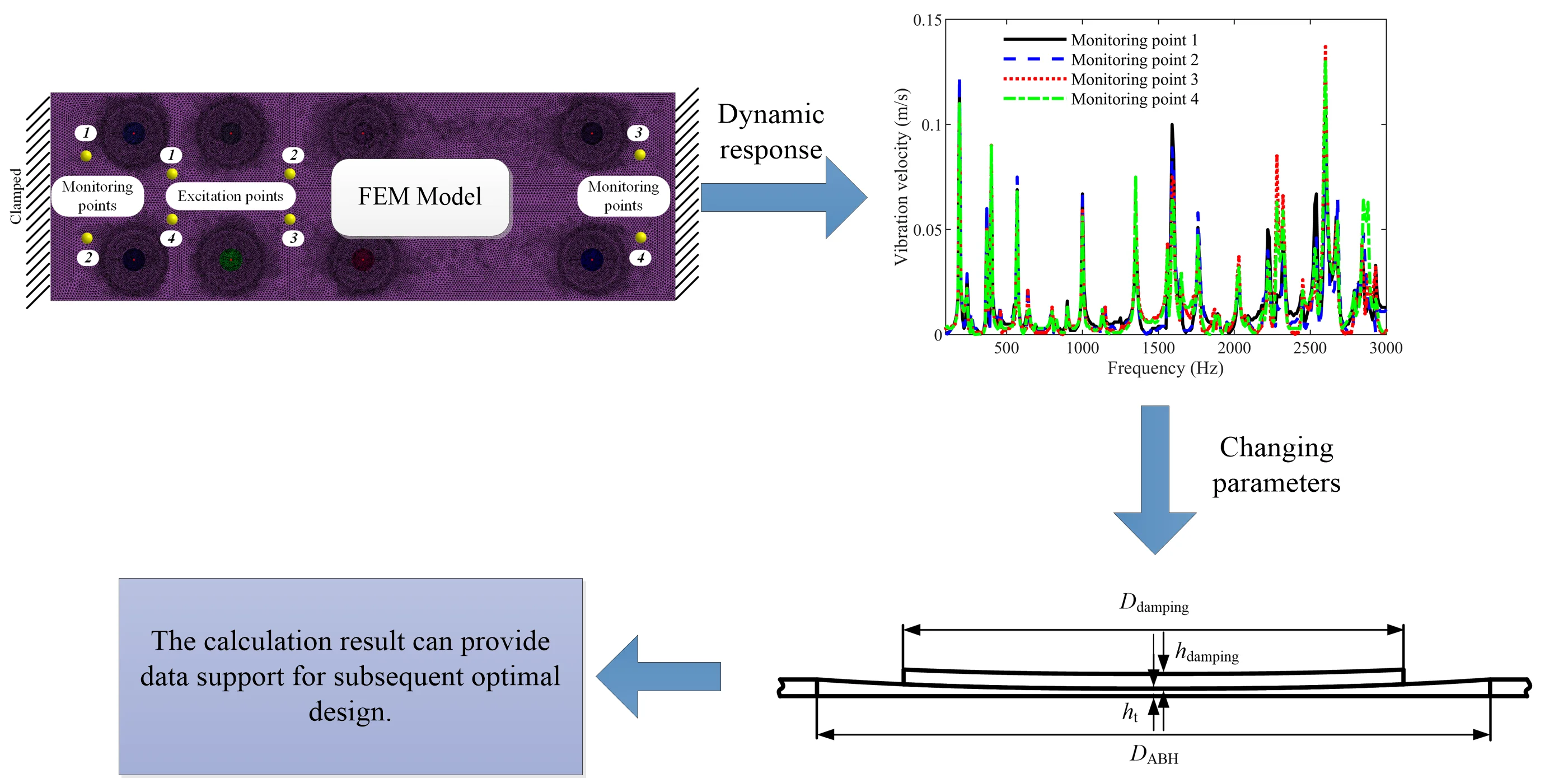
In our previous research, the vibration suppression effect of the acoustic black hole on the refrigerator rectangular support plate has been analyzed [7]. On this basis, the effects of different acoustic black hole parameters and damping layer parameters on the vibration reduction effect of the rectangular support plate of the refrigerator were further analyzed in this paper. The research results can be used to analyze the effects of different acoustic black holes and damping layer geometric parameters, and provide data support for subsequent optimal design.
2. FEM simulation of the rectangular plate embedded with ABHs
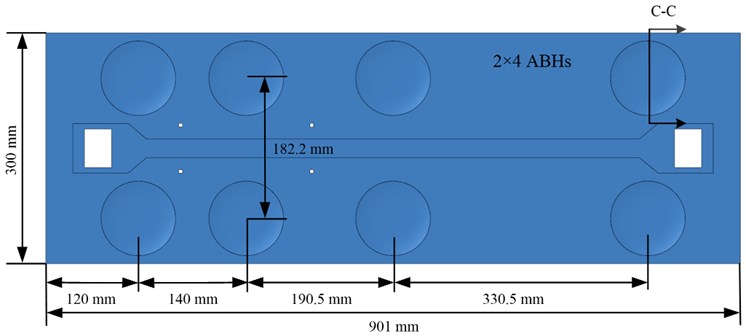
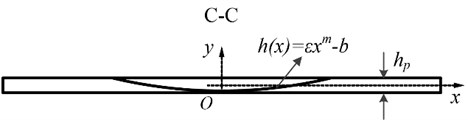
The rectangular plate embedded with 8 two-dimensional acoustic black holes is shown in Fig. 1, and the size of the rectangular plate is 901×300 mm. The upper and lower rows of ABHs are symmetrical about the middle line of the rectangular plate, and the distance between the centres of the two row ABHs is 182.2 mm. For the single ABH in Fig. 1 (a), Fig. (b) shows its profile view. The thickness of the uniform region of the rectangular plate is 1.8 mm, the relationship between the thickness and radius of the ABH region is:
where is a constant, and is the power exponent of the thickness change of the ABH region (), is the distance between the center of the ABH region and the coordinate origin in -axis direction. However, due to the manufacturing technology, there will always be a truncation existing in the actual ABH structure. The thickness of the truncated region can be expressed as:
When the flexural wave propagates from the uniform region of the ABH plate to the ABH region, as the thickness of the plate decreases sharply with a power exponent, the velocity of the flexural wave will also gradually decrease, so as to achieve the concentration effect of the flexural wave. Utilizing the aggregation effect of the ABHs on the flexural wave, the vibration suppression of the rectangular plate can be achieved [8].
Fig. 1Schematic diagram of the rectangular plate embedded with ABHs: a) geometry parameters of the ABH plate, b) profile view of the ABH plate
a)
b)
The second-order tetrahedral unit C3D10 is used to mesh the damping ABH support plate. The grid size of the ABH regions and damping layers is 1 mm, and the mesh in the small curved area of the ABH regions and damping layers is encrypted to ensure a smooth transition from small cells to large cells and the minimum cell size is 0.2 mm during encryption. The curve equation of the acoustic black hole region of the model in Fig. 2 is: 7.12020964467906e-10×x6 – 0.48. It can be calculated from the Eq. (1) and (2), the truncation thickness of the ABH is 0.42 mm, and the maximum diameter of the ABH region is 70.62 mm. The contour curve of the damping layers is the same as the curve of the acoustic black hole region. Therefore, the damping layer can be fully attached on the acoustic black holes. The thickness of the damping layer is 0.89 mm, and the maximum diameter of the damping layer is 33.14 mm. The material parameters of the rectangular plate and the damping layer are shown in Table 1.
Fig. 2The FEM model of the damping ABH plate
Table 1Material parameters of the rectangular plate and the damping layer
Material | Young’s modulus (Pa) | Density (kg/m3) | Poisson’s ratio | Loss factor |
Viscoelastic material | 9×106 | 1812 | 0.45 | 0.4 |
Steel | 2.1×1011 | 7800 | 0.3 | 0.005 |
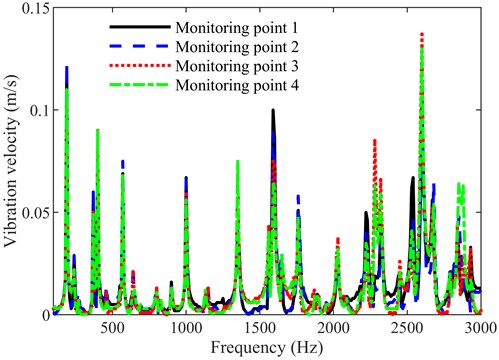
The boundary condition of the rectangular plate is that: the left and right faces are clamped, and the rest faces and edges are free. The force of 6 N is applied at the exciting points 1-4, respectively, and the frequency of the excitation force is 1 Hz-3 kHz (for 1 Hz interval). The vibration velocity responses of the four monitoring points on the damping ABH plate were obtained through calculations in the commercial FEM software LMS Virtual. Lab, which is shown in Fig. 3. It can be seen from Fig. 3 that the frequencies of peak values of the monitoring points 1-4 in the 100 Hz-2 kHz domain are basically the same, and the frequencies of peak values of the monitoring points 1-4 in the 2 kHz-3 kHz domain have some differences. The maximum value of Fig. 3 is the vibration velocity of the monitoring point 3 at 2600 Hz, and the amplitude is 0.137 m/s.
Fig. 3The vibration velocity responses of the four monitoring points on the damping ABH plate
3. Effects of the ABH and damping layer geometric parameters
Fig. 4 shows a schematic diagram of the maximum diameter of the ABH , the truncation thickness of the ABH , the maximum diameter of the damping layer and the thickness of the damping layer . Considering the power index m of the acoustic black hole region, the above five parameters are set as variables. The values of the above five parameters were changed respectively, and then different CAD models of the damping ABH plates were established. The CAD models were meshed with the same sizes of grids in Section 2, and then the meshes were imported into the LMS Virtual. Lab to set the material properties and boundary conditions. The material properties and boundary conditions are the same as the FEM model in Section 2. In addition, the position, amplitude value of the excitation force and position of the monitoring points remain unchanged. Fifteen combinations of different parameters of the maximum ABH diameter, the truncated thickness of the ABH, the power index of the ABH, and the damping layer thickness, the maximum diameter of the damping layer were selected to calculate the vibration velocity response of the four monitoring points. After the FEM calculation was performed, the vibration velocity responses of the four monitoring points around 600 Hz is shown in Table 2. It can be seen from Table 2 that the vibration velocities of the third group is minimal. At this time, the geometric parameters of the acoustic black hole and the damping layer are: 0.61 mm, 5.5, 90.18 mm, 0.99 mm, 27.65 mm.
Fig. 4Schematic diagram of the rectangular plate embedded with ABHs
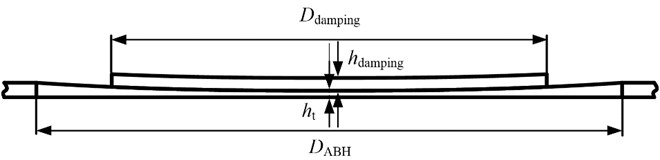
Table 2The vibration velocities of the four monitoring points under different acoustic black hole parameters and damping layer parameters
No. | Value 1 (P1) (m/s) | Value 2 (P2) (m/s) | Value 3 (P3) (m/s) | Value 4 (P4) (m/s) | |||||
1 | 0.37 | 5 | 85.19 | 1.15 | 20.61 | 0.018769 | 0.024649 | 0.021316 | 0.023104 |
2 | 0.56 | 4 | 50.26 | 1.54 | 43.22 | 0.003364 | 0.001296 | 0.013225 | 0.009604 |
3 | 0.61 | 5.5 | 90.18 | 0.99 | 27.65 | 0.002209 | 0.001369 | 0.0004 | 0.000441 |
4 | 0.3 | 3.5 | 78.6 | 1.47 | 35.77 | 0.017424 | 0.0256 | 0.026896 | 0.0289 |
5 | 0.95 | 4.5 | 41.37 | 1.4 | 47.78 | 0.003136 | 0.004489 | 0.015129 | 0.012544 |
6 | 0.88 | 4.5 | 95.01 | 0.85 | 53.92 | 0.004624 | 0.005329 | 0.014161 | 0.010609 |
7 | 0.25 | 2.5 | 98.62 | 0.92 | 38.13 | 0.0169 | 0.024649 | 0.013225 | 0.015876 |
8 | 0.69 | 4 | 66.8 | 1 | 44.85 | 0.002025 | 0.000784 | 0.010404 | 0.008464 |
9 | 0.11 | 5.5 | 63.17 | 1.27 | 23.29 | 0.0225 | 0.018225 | 0.030276 | 0.0225 |
10 | 0.76 | 2 | 42.93 | 1.2 | 25.45 | 0.0036 | 0.005184 | 0.012321 | 0.0121 |
11 | 0.4 | 3.5 | 52.7 | 1.24 | 34.04 | 0.005041 | 0.004761 | 0.003025 | 0.002704 |
12 | 0.73 | 3 | 74.58 | 0.82 | 41.31 | 0.003844 | 0.000361 | 0.012769 | 0.0049 |
13 | 0.33 | 3 | 77.5 | 0.87 | 29.09 | 0.019321 | 0.021316 | 0.025281 | 0.024336 |
14 | 0.79 | 3.5 | 55.86 | 1.38 | 31.6 | 0.0025 | 0.005184 | 0.013456 | 0.013689 |
15 | 0.48 | 5.5 | 86.97 | 1.5 | 56.8 | 0.005625 | 0.007225 | 0.022801 | 0.021025 |
4. Conclusions
In this paper, a group of FEM models for the vibration analysis of the rectangular plate embedded with acoustic black holes were established, and four monitoring points on the ABH plate were selected to calculate their vibration velocity response in 100 Hz-3 kHz frequency interval. The maximum value is the vibration velocity of the monitoring point 3 at 2600 Hz, and the amplitude is 0.137 m/s. In order to study the effects of acoustic black hole geometric parameters and damping layer geometric parameters on the vibration response of the ABH plate, 15 combinations of different parameters of the maximum ABH diameter, the truncated thickness of the ABH, the power index of the ABH, and the damping layer thickness, the maximum diameter of the damping layer were selected to calculate the vibration velocity response of the four monitoring points. The calculation result can help us understand the effects of acoustic black hole geometric parameters and damping layer geometric parameters on the vibration suppression of rectangular plate, and provide data support for subsequent optimal design.
References
-
X. Du, D. Huang, and J. Zhang, “Dynamic property investigation of sandwich acoustic black hole beam with clamped-free boundary condition,” Shock and Vibration, Vol. 2019, pp. 1–14, Aug. 2019, https://doi.org/10.1155/2019/6708138
-
A. Pelat, F. Gautier, S. C. Conlon, and F. Semperlotti, “The acoustic black hole: A review of theory and applications,” Journal of Sound and Vibration, Vol. 476, p. 115316, Jun. 2020, https://doi.org/10.1016/j.jsv.2020.115316
-
C. Zhao and M. Prasad, “Acoustic Black holes in structural design for vibration and noise control,” Acoustics, Vol. 1, No. 1, pp. 220–251, Feb. 2019, https://doi.org/10.3390/acoustics1010014
-
J. Zhang and X. Du, “Numerical investigation of sound transmission loss of circular plates embedded with acoustic black hole,” Vibroengineering Procedia, Vol. 30, pp. 163–167, Apr. 2020, https://doi.org/10.21595/vp.2019.21186
-
E. P. Bowyer and V. V. Krylov, “Damping of flexural vibrations in turbofan blades using the acoustic black hole effect,” Applied Acoustics, Vol. 76, pp. 359–365, Feb. 2014, https://doi.org/10.1016/j.apacoust.2013.09.009
-
P. He et al., “Full-band vibration control of box-type structure with acoustic black hole,” Acta Aeronauticaet Astronautica Sinica, Vol. 41, No. 4, pp. 223350–223350, 2020.
-
X. Du, Q. Fu, J. Zhang, and C. Zong, “Numerical and experimental study on suppression effect of acoustic black hole on vibration transmission of refrigerator compressor,” Applied Sciences, Vol. 11, No. 18, p. 8622, Sep. 2021, https://doi.org/10.3390/app11188622
-
Q. Fu, X. Du, J. Wu, and J. Zhang, “Dynamic property investigation of segmented acoustic black hole beam with different power-law thicknesses,” Smart Materials and Structures, Vol. 30, No. 5, p. 055001, May 2021, https://doi.org/10.1088/1361-665x/abed32
About this article
This work was supported by the National Key Research and Development Program of China (Grant Number 2019YFB2006402) and Scientific Research Foundation for High-level Talents of Nanjing Institute of Technology (Grant Number YKJ202102).
