Numerical investigation of sound transmission loss of circular plates embedded with acoustic black hole

1. Introduction

In the past two decades, the structures embedded with acoustic black hole (ABH) have received wide attention in the application of vibration reduction or noise attenuation, and it also contributes to light-weighting of the structures [1-3]. Above the characteristic frequency of the structure, the ABH can effectively gather the flexural wave in the structure, and while below the characteristic frequency, multiple acoustic black holes are able to improve the low-order modal loss of the structure [4]. Mironov proposed an acoustic black hole pipe structure. By gradually increasing the effective admittance of the pipe along the axial direction, the velocity of the sound wave propagating along the pipe is gradually reduced to zero [5]. Bowyer et al. conducted experimental studies on sound radiation of vibrating rectangular plates containing tapered indentations of power-law profile [6] and found that when a very thin damping material is attached to an acoustic black hole region, the radiated sound power of the structure is reduced by 10 to 18 dB compared with the uniform thickness plate in the frequency range of 1 to 3 kHz [7]. Feurtado experimentally analyzed the influence of the diameter of the damping layer on the radiated sound of rectangular plates with 4×5 array of embedded ABHs in the full frequency range [8]. Then he used experimental and numerical methods to investigate the transmission loss (TL) of plates with embedded ABHs [9] and also calculated the vibro-acoustic coupling properties of the ABH system based on wavenumber transformation method [10].

In this paper, numerical methods were used to analyze the effects of ABH on the sound transmission loss of circular plates. Unlike most other literatures which mainly focus on the responses of ABH structure under point drive excitation, the responses of ABH plates under diffuse sound excitation are represented in this work.

2. Theory of ABH circular plate

A circular plate embedded with a two-dimensional acoustic black hole is shown in Fig. 1. The equation between the thickness of the circular plate and the radius is given by:

where $\epsilon$ is a constant number; $m$ is the taper power, $m\ge$2; $b$ is the distance between the center of the ABH and the origin of the coordinate in the $z$ direction; $h_p$ is the thickness of the uniform region of the plate. The propagation velocity of flexural wave in a thin isotropic plate is:

where $B$ is the bending stiffness, $B=Eh(x{)}^3/[12(1-{\nu }^2)]$; $E$ is the Young’s modulus; $\nu$ is Poisson’s ratio; $\omega$ is the angular frequency; $m$ is the areal density of the plate, $m={\rho }_{m}h\left(x\right)$; ${\rho }_m$ is the density of the plate material. When the flexural wave propagates from the uniform region to the ABH region, the wave velocity will be gradually reduced, the wavelength will be compressed, and the amplitude of the fluctuation will also be gradually increased. As the thickness gradually decreases to zero, the flexural wave propagates here where its cumulative phase reaches infinity, as a result it cannot be reflected back from the center of the ABH region. However, an ideal acoustic black hole cannot be realized in the actual manufacturing due to manufacturing process limitations so that the actual ABH structure must have a truncation. The truncation thickness of the model in Fig. 1 can be expressed as:

Fig. 1A circular plate embedded with a two-dimensional acoustic black hole

When sound waves are incident on a wall or partition, some of them will be reflected and some will be transmitted through the wall or partition. The transmission coefficient is defined as the ratio of transmitted energy to incident energy:

With the condition that the fluids on both sides of the plate are the same, the sound transmission loss of the circular plate can be expressed as [11]:

The sound insulation characteristics of a typical plate can be divided into four parts according to the frequency, which are called the stiffness-controlled region, the mass-controlled region, the coincidence-controlled region, and the damping-controlled region.

3. FEM modeling of TL analysis

The sound insulation problem of an ABH circular plate is a vibro-acoustic coupling process. The vibro-acoustic coupled equation of this procedure in the form of a matrix can be expressed as:

where ${\mathbf{{\rm K}}}_s$, ${\mathbf{M}}_s$, ${\mathbf{C}}_s$ are the stiffness matrix, mass matrix and damping matrix of the unconstrained part of the structural mesh, ${\mathbf{{\rm K}}}_c$ is the coupling stiffness matrix, $\left\{F_{si}\right\}$ is the excitation load, which includes the contribution of the constraint portion of the structure, the known load and the external sound pressure load $p$ perpendicular to the surface of the structure. Besides, ${\mathbf{M}}_c$ is the coupled mass matrix, $\left\{F_{ai}\right\}$ is the excitation load, which contains the known sound pressure, the sound source in the acoustic field, and the contribution of the vibration velocity boundary.

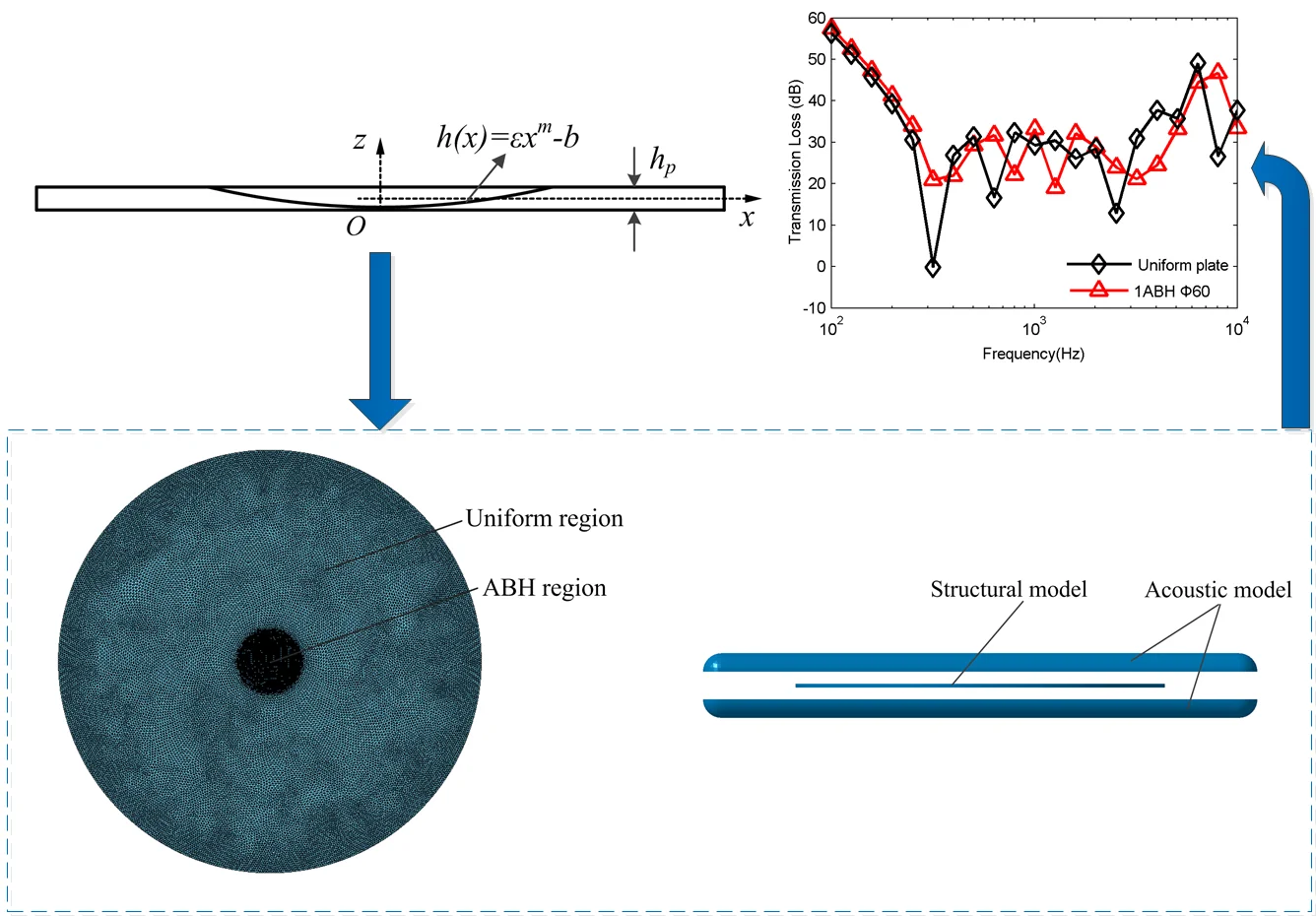
The geometric parameters of the model used for finite element analysis are shown in Table 1. The diameter and thickness of the circular plate is 400 mm and 4 mm, the power index of ABH is $m=$2, the diameter of the ABH region is 60 mm, and the truncation thickness is 0.5 mm.

Fig. 2 shows the FEM model of the ABH circular plate and the vibro-acoustic coupled model for TL analysis. The ABH circular plate is meshed by a tetrahedral mesh, and the mesh size of the uniform region is 2 mm. In order to improve the calculation accuracy, the grid of the ABH region has a basic size of 1 mm and encrypts the mesh in the small curved area with a minimum size of 0.2 mm, thereby ensuring the elements on the smaller surface transition well to the units on adjacent large surfaces. The acoustic model has a size of 0.6×0.6×0.02 m. The calculated frequency has a corresponding relationship with the grid cell size. For the linear finite element model, the side length of the largest cell must be less than 1/6 of the wavelength corresponding to the highest calculated frequency, that is $L\le c/6f_{\mathrm{m}\mathrm{a}\mathrm{x}}$. In this paper, the calculation frequency of the transmission loss is 0-10 kHz, so the cell length of the mesh should not be greater than 5.6 mm. Finally, the mesh size of the acoustic finite element model of this paper is selected as 4 mm.

Fig. 2TL analysis model of an ABH plate

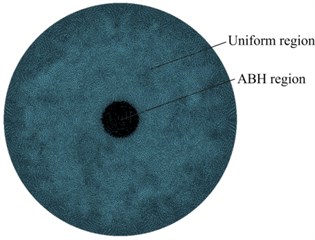
a) Structural model of the ABH plate

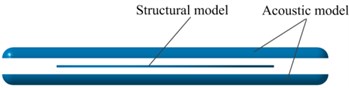
b) Vibro-acoustic coupling model

The FEM simulation was performed using the commercial software LMS Virtural.Lab. The acoustic model below the plate in Fig. 2(b) represents the reverberation chamber, and the acoustic model above the plate simulates the anechoic chamber. The ABH region of the circular plate is on the side close to the anechoic chamber, and the boundary condition of the periphery of the circular plate is clamped. A reverberation sound source is generated in the reverberation chamber, and the sound is transmitted to the anechoic chamber through the ABH plate, and finally passes through the outer wall surface of the anechoic chamber and radiates outward without reflection. The faces of the two acoustic meshes close to the structural mesh are respectively coupled with the corresponding faces of the structural mesh and the remaining faces of the two acoustic meshes are respectively applied with a diffuse sound field on the side of the reverberation chamber and a zero reflection surface on the side of the anechoic chamber by the Automatic Matched Layer (AML) method. The transmission loss of the ABH plate can be obtained by computing the sound power incident on the ABH circular plate and radiated from the plate to the anechoic chamber.

The material parameters of the ABH circular plate are shown in Table 2. The first-order resonant frequency and the coincidence frequency of the ABH circular plate can be calculated to be approximately 350 Hz and 2900 Hz according to LMS Virtural.Lab. Therefore, the calculated frequency of 0-10 KHz selected in this paper covers all characteristic frequency regions from the stiffness-controlled region to the damping-controlled region.

4. Results of TL simulation

The TL of an ABH circular plate with a diameter of 60 mm embedded in the center was calculated and compared with the sound transmission loss of the uniform circular plate, as shown in Fig. 3. It can be seen from Fig. 3 that, below the first-order resonance frequency, the TL of the circular plate embedded with the 2-D ABH is improved compared with the uniform circular plate and both the TLs of the two plates decrease as the frequency increases. At the first-order resonance frequency, the acoustic loss of the circular plate embedded with the acoustic black hole is greatly improved compared with the uniform circular plate. The difference between the TL of the ABH circular plate and the uniform circular plate at this frequency is 21.13 dB. In the mass-controlled region, the TL of the circular plate embedded with ABH is larger at some frequencies; while at other frequencies, the TL of the uniform circular plate is larger, indicating that the sound insulation performance of the ABH circular plate is not improved overall in this characteristic region. At the coincidence frequency, the TL of the ABH circular plate is 8.31 dB higher than that of the uniform circular plate. While in the damping-controlled region, the TL of the ABH circular plate is not improved overall, but at a certain frequency, for example, 8 kHz, there is an increase of 20 dB for the TL of the ABH circular plate.

Fig. 3TL of a circular plate embedded with a diameter of 60 mm acoustic black hole and the uniform circular plate

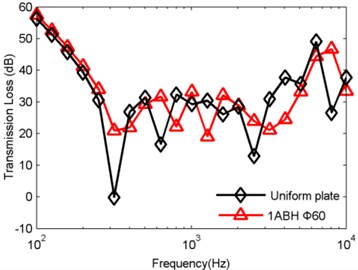
a) TL values from 0 to 10 kHz

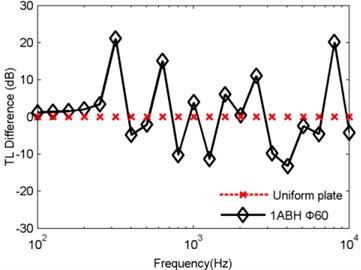
b) TL differences of the two plates

5. Conclusions

In this study, a series of vibro-acoustic coupling finite element models for sound transmission loss (TL) analysis of ABH circular plates were established by Automatic Matched Layer (AML) method. The simulation results show that the circular plate with a single ABH embedded in the center position can significantly improve the sound transmission loss in stiffness-controlled region, and at the first-order resonance frequency and some frequencies in damping-controlled region. At the coincidence frequency, the TL of the ABH circular plate is 8.31 dB higher than that of the uniform circular plate. While in the damping-controlled region, the TL of the ABH circular plate is not improved overall, but at a certain frequency, for example, 8 kHz, there is an increase of 20 dB for the TL of the ABH circular plate.