Study on vibration characteristics of badminton racket embedded in acoustic black hole structure

1. Introduction

Acoustic black holes can manipulate elastic waves through changes in the impedance of the structure itself, thereby reducing or even avoiding the reflection of bending waves from the edges of the structure to suppress its vibration [1]. For a plate or beam structure, when bending waves propagate on an acoustic black hole structure with a gradually decreasing thickness, the wave velocity will gradually decrease and the vibration amplitude will gradually increase. According to the theory of geometric acoustics, if the change in local thickness of the structure satisfies a power-law relationship ($h\left(x\right)=\epsilon x^m,m\ge 2$), the propagation speed of the bending wave will also decrease to zero when the local thickness of the acoustic structure decreases to zero [2-4]. In other words, at this point, the propagation of the bending wave will stop without reflection. So, all the vibration energy in the structure will converge at the edge tip, avoiding the resonance vibration of the main structure. However, in practice, due to the limitation of processing technology, truncation error will inevitably occur at the tip of acoustic black hole structure, that is, zero thickness cannot be realized at all, which will destroy the ability of acoustic black hole effect to achieve zero reflection of curved waves [5-8]. Krylov et al. [3] showed that when the local thickness of the edge of the beam structure followed a certain power law relationship with the local position, only a very small number of damping materials needed to be pasted on the edge of the structure, the vibration energy gathered at this position could be effectively dissipated, thus effectively improving the vibration and noise reduction effect of the acoustic black hole structure. Therefore, to control the bending wave and concentrate its energy, it can be realized by changing the local thickness of the structure itself and attaching a small amount of damping material. Krylov and Winward [7, 8] conducted experimental research on one-dimensional acoustic black hole structures, and found that the maximum resonance peak attenuation reached 20 dB when a damping material was applied, demonstrating the enormous potential of acoustic black holes in vibration suppression applications. Subsequently, Kralovic and Krylov [9] experimentally observed a bar with a quadratic exponential change in thickness and a damping material on the tip, which also verified the wide-band vibration attenuation effect of acoustic black hole structure. Denis et al. [10-11] experimentally studied the modal loss factor of a one-dimensional acoustic black hole structure with truncation, demonstrating that the presence of acoustic black holes in the structure significantly increases the modal loss factor. Overall, the above research indicates that the acoustic black hole effect has good robustness [12], and can still have good vibration suppression effects even in the presence of certain errors in machining accuracy.

In this context, this article focuses on the vibration reduction of badminton rackets and designs a racket model with an embedded one-dimensional acoustic black hole structure. Based on finite element simulation analysis, the broadband vibration reduction characteristics of a racket structure with a small amount of damping material attached to the tip were studied. At the same time, the influence of the truncation of the acoustic black hole structure and the damping parameters such as the thickness and distribution of the damping layer on the one-dimensional acoustic black hole effect were also discussed. The research results can provide reference for the engineering application of acoustic black hole structures.

2. Analysis of vibration characteristics of racket with acoustic black hole structure

2.1. Modeling of the racket with acoustic black hole structure

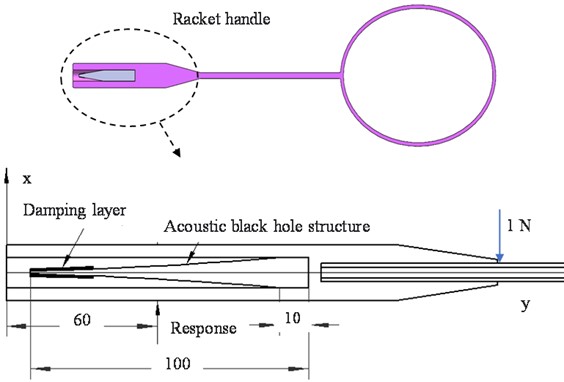
In this section, based on ABAQUS steady-state dynamic analysis, frequency response function and overall modal loss factor of the system are used as the criteria to evaluate the vibration reduction effect in wide-band steady-state vibration. As shown in Fig. 1, the acoustic black hole rod and ball rod are both made of steel, with the elastic modulus of 210 GPa, the density of 7800 kg/m³, the Poisson’s ratio of 0.3, and the structural damping of 0.005. The handle part is made of wood, whose elastic modulus $E=$ 11 Gpa, density $\rho =$ 540 kg/m³, Poisson’s ratio $v=$ 0.3, damping coefficient ${\xi }_2=$ 0.02. The elastic modulus of the damping material is set to 1 GPa, the material density is 950 kg/m³, the Poisson’s ratio is 0.3, and the structural damping is 0.3. In addition, tie constraints are applied at the racket rod and handle. The mesh division of the finite element model adopts C3D8R with completely free boundary conditions, and a vertically downward harmonic driving force with an amplitude of 1 N is applied at the right end of the handle. The sweep frequency range set to 300 Hz-9000 Hz.

Fig. 1The badminton racket model with one-dimensional acoustic black hole structure

2.2. Simulation analysis

2.2.1. Vibration response analysis of racket embedded in acoustic black hole structure

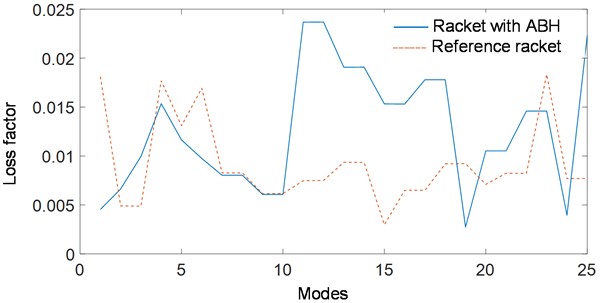
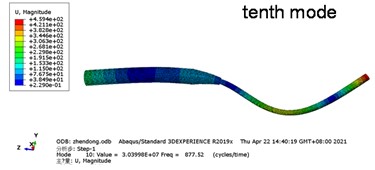
From Fig. 2, the badminton racket with an additional acoustic black hole structure exhibits good vibration reduction performance over a wide frequency range. In addition, from the comparison of modal loss factors in Fig. 3, it can be found that starting from the tenth resonant frequency, the damping effect brought by the racket rod embedded with an acoustic black hole structure is significantly better than that of the reference rod. This is because the first ten modes of vibration are mainly bending, and the main mode of vibration of the structure is not in the acoustic black hole region, so the damping layer has little impact on the overall damping effect of the system. However, starting from the eleventh mode, the acoustic black hole structure begins to accumulate a large amount of vibrational energy, thereby increasing the loss factor of the entire system. Moreover, each mode after the tenth order is dominated by local vibrations in the acoustic black hole region, as shown in Fig. 4.

Fig. 2Comparative analysis of vibration response of the racket

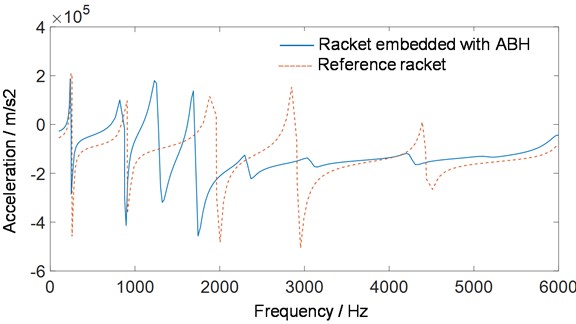
Fig. 3Comparative analysis of loss factors

2.2.2. Effect of tip truncation on one-dimensional acoustic black hole effect

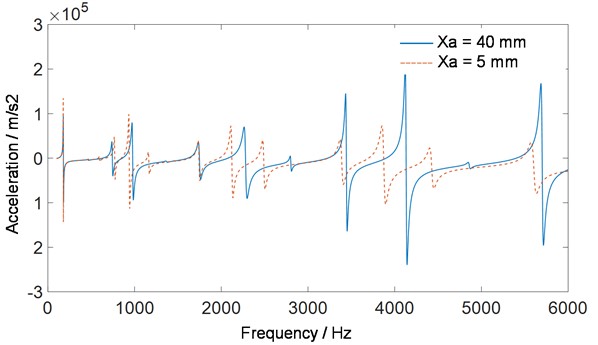
As shown in Fig. 5, in the case of no damping layer, when the truncation of the acoustic black hole rod is relatively small, in the frequency response characteristics of the acoustic black hole rod, except formant shift and some new formants, the acoustic black hole rod shows no significant damping effect in the wide band region, which may be caused by the truncation of the end region of the acoustic black hole. In addition, the results show that the suppression effect of acoustic black hole structure on vibration becomes better and better with the decrease of truncation length (that is, the thickness of acoustic structure). On the one hand, the reduction of truncation thickness makes the deformation of acoustic black hole structure approach the edge; on the other hand, the reduction of truncation thickness will cause the reduction of structural mass and stiffness, and the vibration of acoustic black hole will be enhanced under the same excitation.

Fig. 4The modes of the racket with acoustic black hole structure

a)

b)

c)

d)

Fig. 5Comparison of different truncation response curves

2.2.3. Effect of damping layer on one-dimensional acoustic black hole effect

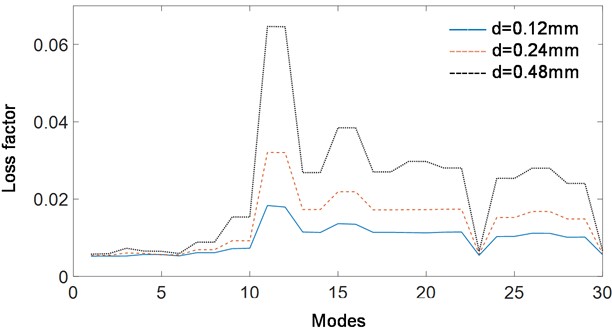
In order to improve the low frequency performance of acoustic black hole effect, the influence of damping layer thickness $d$ on vibration suppression and modal loss factor are shown in Figs. 6-7. The results show that increasing the thickness of the damping layer can effectively reduce the vibration amplitude and increase the modal loss factor. However, since the deformation of the first mode of the acoustic black hole beam is far away from the acoustic black hole region at the edge, changing the thickness of the damping layer has little effect on the radiated acoustic power near the first natural frequency. It is also worth noting that the presence of the damping layer and the change in its thickness do not change the position of the peak of the curve, which means that the damping material cannot increase the bandwidth of the acoustic black hole effect by changing the cutoff frequency of the acoustic black hole structure.

Fig. 6Response of ABH with different damping thicknesses

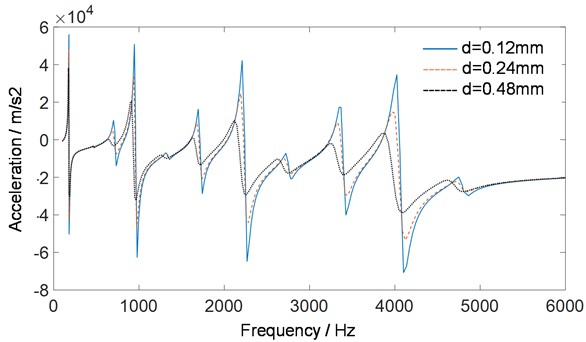
Fig. 7Modal loss factors with different damping thicknesses

3. Conclusions

1) The damping layer attached to the tip of the non-ideal acoustic black hole structure can well weaken the destruction of the acoustic black hole effect caused by truncation, and thus enhance the damping property of the structure. In addition, the presence of the damping layer and the change of its thickness do not change the position of the peak of the curve, that is, the damping material cannot increase the bandwidth of the acoustic black hole effect by changing the cutoff frequency of the acoustic black hole beam.

2) The results show that the larger the damping layer thickness is, the closer the damping layer is to the tip of the acoustic black hole structure, and the more obvious the damping effect is.

3) The vibration reduction design with one-dimensional acoustic black hole structure has a very effective application prospect, such as the vibration isolation of tennis racket, badminton racket, golf club. Such a structure not only shows good vibration damping characteristics in the wide band range, but also ensures the lightweight structure, which can avoid too much added mass on the negative impact of user experience.