Study on semi-active particle damping technology for offshore platform truss structure

Xia, Zhaowang; Kai, Jiemao; Wang, Xuetao; Shao, Guangsheng; Jiang, Wenan; Sun, Yao

doi:10.21595/jve.2016.17365

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 November 2016

Check for updates

Study on semi-active particle damping technology for offshore platform truss structure

Zhaowang Xia¹

Jiemao Kai²

Xuetao Wang³

Guangsheng Shao⁴

Wenan Jiang⁵

Yao Sun⁶

^{1, 2, 3, 4, 6}School of Energy and Power Engineering, Jiangsu University of Science and Technology, Zhenjiang, China

⁵School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China

Corresponding Author:

Yao Sun

Cite the article Download PDF

Downloads 1815

WoS Core Citations 10

CrossRef Citations 9

Abstract

The vibration reduction device for the offshore platform truss structure has exposed to long term high-energy ultraviolet light and salt spray radiation, the traditional viscoelastic damping technology is easy to aging and failure, and its operational lifetime is limited. The semi-active particle damping technology has the advantages of high temperature resistance, anti-aging and so on, at the same time it is also able to adapt the changes of external complex load. The coupling simulation algorithm was used in this paper to study on vibration reduction performance of semi-active particle damping technology for the offshore platform truss structure. The control strategy, simulation algorithm and key parameters of semi-active particle damping are investigated to analyze the vibration reduction effect of the offshore platform truss structure with semi-active particle damper. The results have shown that the semi-active particle damping has a better effect of vibration reduction compared with the passive particle damping. In addition, the control strategy in different frequency bands has different vibration reduction effects to the system; and the simulation has a good agreement with the experimental results.

1. Introduction

Offshore platform as the basic facility for the exploitation of petroleum and natural gas resources, the base of production and life on the sea, its safeness is vital importance. The offshore platform truss structure will be inevitably affected by wind, waves, ocean currents, and ice seismic [1], and under this harsh environment for long term [2], this may create noticeable vibration to the offshore platform truss structure which can increased the fatigue damage, deduced the reliability of the system, affected the structure safeness and durability. The vibration control technology of offshore platform has got more and more attention [3, 4], at present viscoelastic damping technology is often to be used, which has good vibration reduction effect [5], but due to the devices long term exposed to long term high-energy ultraviolet light and salt spray radiation [6, 7], viscoelastic damping materials are easy to aging, failure and reduce its operational life time [8].

The traditional particle damping technology is a new type of passive damping technology [9, 10], which has the advantages of vibration reduction frequency bandwidth [11], simple structure [12, 13], anti-aging [14], high temperature resistance [15], and so on. Due to the excellent performance of particle damping technology [16], it has great application prospects in many important engineering projects [17]. Particle damping technology has been highly valued by governments and industries [18], and has invested enormous financial and material resources to carry out research in this area [19]. The United States military has listed it as the top priority development project [20].

At present, the theoretical research of particle damping technology is focused on the passive particle damping technology [21, 22], but in recent years, people found that the vibration reduction effect of particle damping technology in low frequency band is not very good, in addition it is difficult to adapt the change of load in complex external environment [23, 24]. The semi-active particle damping technology may improve the vibration reduction effect and the ability of particle damping adapt to the outside complex load. Binoyet al. [25] first presented semi-active particle-based damping system. In this paper, the semi-active particle damping technology is used for vibration reduction for the offshore platform truss structure.

In this paper, the semi-active particle damping is applied to improve the vibration reduction effect of the offshore platform truss structure. The control strategy, the simulation algorithm and the key parameters of semi-active particle damping are investigated to analyze the vibration reduction effect of the offshore platform truss structure with semi-active particle damper. Moreover, the research may also provide some guidelines of semi-active particle damping technology for the vibration reduction of complicated structures in harsh environment.

2. Coupling simulation algorithm

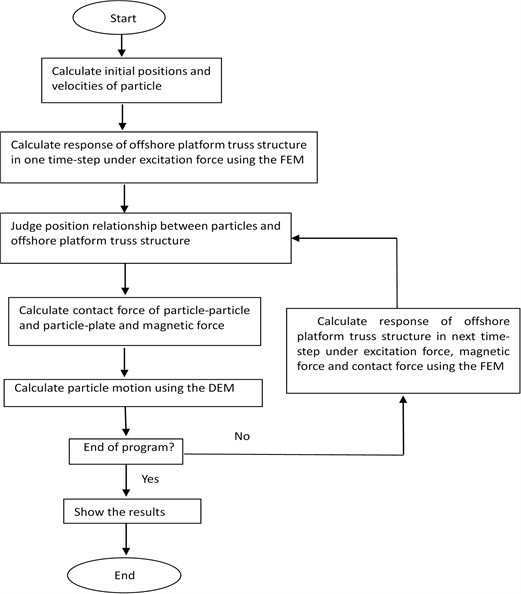
The discrete element method (DEM) is based on the hypothesis that the disturbances only propagate from a particle to other particles that are in direct contact during a single time step. Therefore, instead of solving the same number of simultaneous equations as contact points, the equation of motion for each particle can be solved independently in each time step. In this paper, the motions of particles are calculated by using the DEM in each time-step that is set small enough to consider the velocity, acceleration, excitation force and the forces exerted on the offshore platform truss structure of every particle as constant approximately. A finite element model of the offshore platform truss structure is developed in NASTRAN software. The calculations of the offshore platform truss structure with semi-active particle dampers are alternately performed in the DEM and the FEM. The response of the structure is calculated to study the damping effect of semi-active particle damper by using the NASTRAN software. The flow chart of numerical simulation is shown in Fig. 1.

Fig. 1Flow chart of the coupling simulation algorithm for semi-active particle damper system

2.1. The contact force and magnetic force

The contact force in the DEM is expressed by [2]:

1

F_{n} = k_{n} {δ_{n}}^{\frac{3}{2}} + c_{n} {δ_{n}}^{\frac{1}{4}} {\dot{δ}}_{n},

where $k_{n}$ is the normal stiffness, the particle stiffness is used in the contact model which relates the contact force and relative displacement, $c_{n}$ is the normal viscous damping coefficient, $δ_{n}$ is the normal overlap distance.

Except the normal forces, the tangential forces may be created when a particle slides along another one or along the cavity wall. Using an incremental form, the tangential component $F_{s}$ ofthe contact force is expressed by:

2

F_{s} = \{\begin{matrix} F_{s} (t), & μ F_{n} > F_{s} (t), \\ - μ F_{n}, & μ F_{n} \leq F_{s} (t), \end{matrix}

3

F_{s} (t 0 = F_{S} (t - ∆ t) - k_{s} v_{s} ∆ t - c_{s} v_{s},

where $k_{s}$ is the tangential stiffness, $v_{s}$ is the relative velocity of two particles in the tangential direction; $∆ T$ is time-step; $c_{s}$ is the tangential damping coefficient.

Time-step for the DEM simulation is given by:

4

Δ t = \frac{π R}{0.1631 γ + 0.8766} \sqrt{\frac{ρ}{G}},

where $G$ is the shear modulus, $R$ is the radius of particle.

The magnetic force of the particles is given by [26]:

5

F = \frac{3 μ_{0}}{4 π r^{4}} [(N \cdot N^{'}) - 3 (N \cdot r_{0}) (N^{'} \cdot r)],

where $N$ is the magnetic dipole, $r$ is the distance of two particles, $r_{0}$ is the distance unit vector, $μ_{0}$ is the Permeability of vacuum,

In constant electromagnetic field, the magneticdipole force of inter particles at different layer inside the cylindrical particle damper is gravitational force, the magnetic dipole force between inter particles at same layer inside the cylindrical particle damper is repulsion force. The current intensity determines the inter particle acting force intensity. Therefore, the pressure distribution of particles in the particle damper can be changed by changing the current intensity, in order to control the damping performance of particle damper.

2.2. Semi-active control strategy

As the relationship among the particle damping force, excitation current, and relative velocity is nonlinear in the semi-active particle damper system, whether the damping force can be described as separated form of system status and of adjustable parameters, so far there is no relevant literature report. This paper will be based on a large number experimental data, and use two control strategies to analyze the vibration characteristics of semi-active particle damper system.

2.2.1. On-off control strategy

On-off control strategy is only required to detect the state of the system, based on the condition to carry on the switch function. The switching of the electric current only happened in between the finite discrete value.

The following conclusion can be obtained by analyzing the experimental data of semi-active particle damper system: 1) near the resonance, the greater the damping, the better the vibration isolation effect; 2) the excitation current is greater than or equal to 0; 3) the relationship between the damping force and excitation current is: the greater the current, the greater the particle damping force. So, the on-off control strategy is given by:

6

i = \{\begin{array}{l} i_{m a x}, \dot{x} ({\dot{\bar{x}}}_{b} - \dot{x}) > 0, \\ 0, \dot{x} ({\dot{\bar{x}}}_{b} - \dot{x}) \leq 0, \end{array}

where $\dot{x}$ is the velocity of semi-active particle damper, ${\dot{\bar{x}}}_{b}$ is the average velocity of particles. The advantage of on-off control strategy is easy to implement.

2.2.2. Revised on-off control strategy

The on-off control strategy has not taken the consideration of the contact force of particles. The contact force is closely related to the relative displacement, so the revised on-off control strategy is:

7

i = \{\begin{array}{l} i_{m a x}, ({\bar{x}}_{b} - x) ({\dot{\bar{x}}}_{b} - \dot{x}) > 0, \\ 0, ({\bar{x}}_{b} - x) ({\dot{\bar{x}}}_{b} - \dot{x}) \leq 0, \end{array}

where $x$ is the displacement of semi-active particle damper, ${\bar{x}}_{b}$ is theaverage displacement of particles.

2.3. Description of motion

The three-dimensional DEM used here is based on the iterative method. The particle displacement and contact area are small relative to the particle sizes. The DEM is applied to simulate the motion and interaction of particles, and the motion of primary structure is calculated by using the FEM. The Newton’s law is performed for each particle, based on the resultant force and resultant moment on each particle. The equations of motion for the $i$ th particle are given as:

8

F_{i} = m_{i} {\ddot{x}}_{i},

9

M_{i} = I_{i} {\ddot{θ}}_{i} .

In Eqs. (8-9), $F_{i}$ is the resultant force vector; $m_{i}$ is the mass of ith particle; ${\ddot{x}}_{i}$ is the acceleration vector of the particle; $M_{i}$ is the resultant moment; $I_{i}$ is the moment of inertia; ${\ddot{θ}}_{i}$ is the angular acceleration vector.

Given the resultant forces and moments, the position of the $i$ th particle in one time-step $Δ t$ is updated based on the equation:

10

x_{i}^{(t + Δ t)} = x_{i}^{(t)} + {\dot{x}}_{i}^{(t + Δ t / 2)} Δ t,

11

θ_{i}^{(t + Δ t)} = θ_{i}^{(t)} + {\dot{θ}}_{i}^{(t + Δ t / 2)} Δ t,

where the mid-interval quantities are computed based on central finite difference scheme of the velocities:

12

{\dot{x}}_{i}^{(t + Δ t / 2)} = {\dot{x}}_{i}^{(t - Δ t / 2)} + \frac{F_{i}}{m_{i}} Δ t,

13

{\dot{θ}}_{i}^{(t + Δ t / 2)} = {\dot{θ}}_{i}^{(t - Δ t / 2)} + \frac{M_{i}}{I_{i}} Δ t .

3. Experimental results

3.1. Experimental setup

The offshore platform truss structure with semi-active particle damper is shown in Fig. 2. The overall height is 900 mm, design a platform for each 300 mm height. The structure selected Ø32×3 304 stainless steel pipe as main column, selected Ø22×2 304 stainless steel pipe as stiffened tubular and structure tubular. Installed a motor at the bottom of the offshore platform truss structure, the motor speed is 2000 rpm, an extra eccentric mass block had installed on the motor in order to increase the excitation. The acceleration sensor is used to test the acceleration of the motor base and each measuring points.

This paper mainly studies the parameters of the semi-active particle damper (the filling ratio and the particle diameter), control current and control strategy (on-off control and revised on-off control) to the influence law of the offshore platform truss structure vibration reduction effect. In the experiment, the semi-active particle damper is made of plastic material, and its inner diameter is 70 mm, the electrified coil is 8000 ring, as shown in Fig. 2. A represented the Centre vibration of the offshore platform truss structure. B denotes the edge vibration of the offshore platform truss structure. C stands for the vibration of supporting point of the offshore platform truss structure.

The semi-active particle damper is filled by the steel particles in different diameters. The density of the steel particle is 7800 kg/m³. The filing ratios of particles are set to be 0 % (without particles), 10 %, 20 %, 30 %, 40 %, 50 %, 60 %, 70 %, 80 %, 90 % and 100 %, respectively. The particle diameters are set to be 0.1 mm, 0.3 mm, 0.5 mm, 0.7 mm and 1 mm, respectively. The control currents are set to be 0.1 A-0.5 A, step length 0.1 A. The particles material are set to be aluminum alloy particles (2600 kg/m³), steel particles (7800 kg/m³), lead particles (11300 kg/m³) and tungsten carbide particles (14800 kg/m³).

Fig. 2Photograph of experimental setup

The effect of semi-active particle damper to the vibration performance of the offshore platform truss structure has shown in Fig. 3. The vibration attenuation is obvious from the motor to the platform, and it is proved that the particle damper has a better effect of vibration reduction. The following section will analyze the influence law of particle damper parameters to the offshore platform truss structure vibration characteristics.

Two semi-active particle dampers are installed on the offshore platform truss structure. The vibration transmissibility of point A has shown in Fig. 4 and Fig. 5 respectively, when the filling ratio is 70 %, the diameter of steel particle is 0.5 mm, electrified coil is 8000 ring, current is 0 A and 0.1 A respectively. The result of the experiments is consistent with the calculated result with the coupling simulation algorithm. The average error of the largest ten resonance amplitude is 2.7 dB. Fig. 4 and Fig. 5 indicate that calculated results with the coupling simulation algorithm reproduce the experimental results with reasonable accuracy, when the semi-active particle damper is controlled with current and without current.

Fig. 3Effects of particle damper on truss structure vibrations

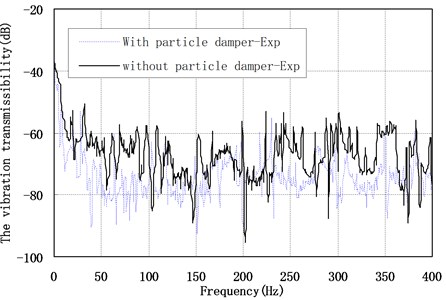
Fig. 4The vibration transmissibility of point A with 0 A current

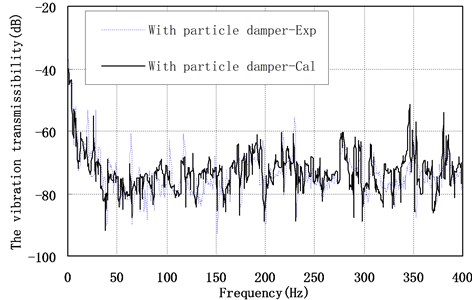
Fig. 5The vibration transmissibility of point A with 0.1 A current

4. The effect of parameters to the vibration characteristics of the offshore platform truss structure with semi-active particle damper

4.1. Control current

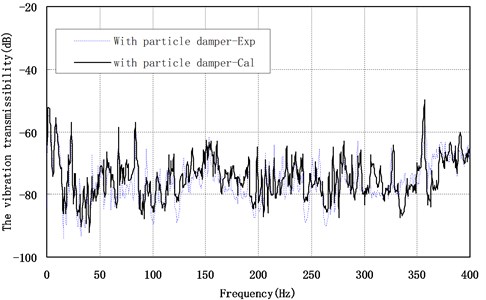
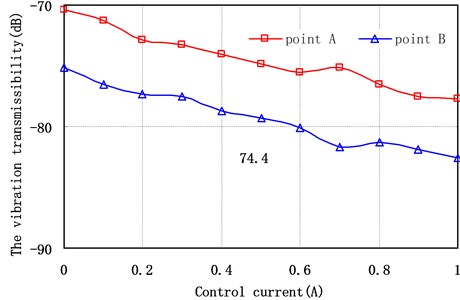
The coefficients of restitution for both particle-structure and particle-particle contacts are chosen as 0.78. The granular particles in each particle damper used in this simulation are steel spherical particles, and are of uniform diameter ( $d =$ 0.5 mm). The particle filling ratio is 70 %. The electrified coil is 8000 ring. The vibration transmissibility of A point has shown in Fig. 6, and the vibration transmissibility of point A and B affected by the control current (0-0.5A) has shown in Fig. 7. They indicate that: (1) when the frequency range is 0-150 Hz, with the increase of control current, the vibration transmissibility of the offshore platform truss structure decrease, which means that the vibration reduction effect of the system is better. (2) When the frequency range is 150-400 Hz, the effect of control current is not stable to the vibration reduction effect.

Fig. 6Vibration transmissibility of the point A versus the control current

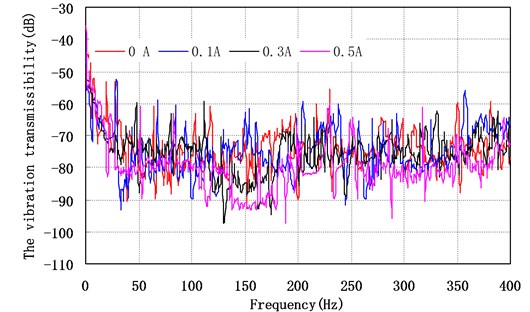
Fig. 7Vibration transmissibility of different measuring points versus the control current

4.2. Control strategy

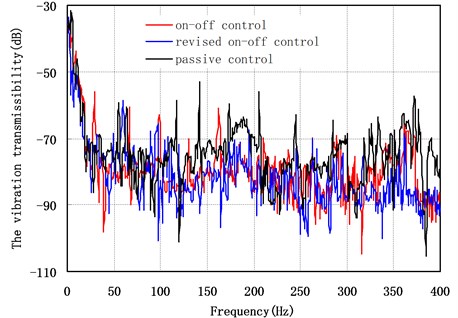
The filling ratio is 50 %. The diameter of steel particle is 0.1 mm. Electrified coil is 8000 ring. The vibration transmissibility of point A and point B of the offshore platform truss structure versus the passive particle damper (control current as 0.3 A), on-off control strategy and revised on-off control strategy (the control current switching between 0 A and 0.3 A) have shown in Fig. 8 and Fig. 9 respectively. They indicate that: (1) the vibration reduction effect with revised on-off control strategy at all frequency ranges is better than with on-off control strategy, and the vibration transmissibility decreased 4.2 dB in the whole frequency range. (2) The vibration reduction effect of B point with revised on-off control strategy also is better than with on-off control strategy on the whole, but the vibration reduction effect is not obvious, and the vibration reduction effect of the offshore platform truss structure under on-off control strategy near the 300 Hz has better effect. (3) The vibration reduction effect of the offshore platform truss structure under revised on-off control strategy and on-off control strategy has a better effect compare with passive control on the whole, but the vibration reduction effect is not obvious under semi-active control when the frequency is less than 100 Hz.

Fig. 8Vibration transmissibility of the point A versus the control strategy

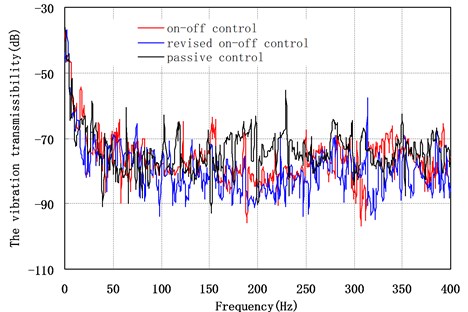
Fig. 9Vibration transmissibility of the point B versus the control strategy

4.3. Particle diameter

When the particle material is steel, particle filling ratio as 50 %, the vibration transmissibility of point A point and B of the offshore platform truss structure versus the particle diameters have shown in Fig. 10 and Fig. 11 respectively. They indicate that: (1) with the increase of particle diameter, the vibration transmissibility of the offshore platform truss structure is gradually reduced, the vibration reduction effect of the offshore platform truss structure has become better. (2) when the frequency range is 100-400 Hz, the effect of particle diameter to vibration transmissibility is obvious. This is because the vibration of the particles is bigger in high excitation frequency. The larger the diameter of particles, the greater the energy dissipation of collision and friction, the better the vibration reduction effect of the offshore platform truss structure. (3) when the particle diameter less than 0.5 mm, the particle diameter has notable effect to the vibration transmissibility of the offshore platform truss structure. When the particle diameter is greater than 1mm, the effect to the vibration transmissibility has become less notable.

4.4. Filling ratio

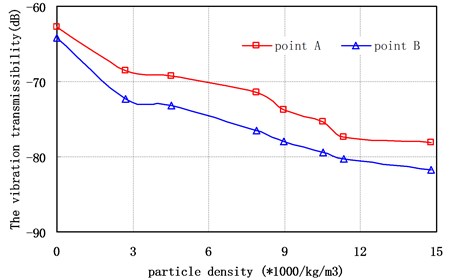
Particle material is steel. Particle diameter is 0.5 mm. The vibration transmissibility of point A and point B of the offshore platform truss structure versus the filling ratio have shown in Fig. 12 and Fig. 13 respectively. They indicate that: (1) with the increase of the filling ratio, the vibration reduction effect of the offshore platform truss structure slightly increased at the beginning, but after that the vibration reduction effect decreased. When the filling ratio reached around 80 %, the offshore platform truss structure has the best vibration reduction effect. The average vibration transmissibility has reduced 18.2 dB. (2) when the filling ratio reached 100 %, the vibration reduction effect of the system has greatly reduced. Mainly because of the motion restriction of particle in cavity, so there is no collision between particles, only through friction between the particles to dissipate energy. Its average vibration transmissibility with 100 % filling ratio has reduced 1.2 dB than without particle damper (0 % filling ratio). (3) filling ratio is an important parameter of the offshore platform truss structure with particle damper.

Fig. 10Vibration transmissibility of the point A versus particle diameter

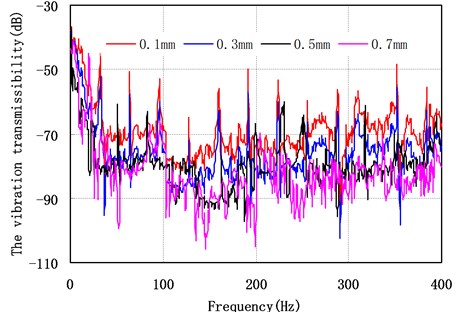
Fig. 11Vibration transmissibility of different measuring points versus particle diameter

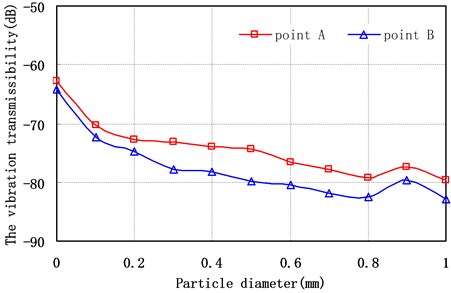
Fig. 12Vibration transmissibility of the point A versus filling ratio

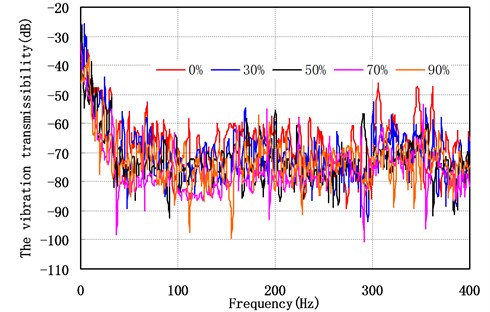
Fig. 13Vibration transmissibility of different measuring points versus filling ratio

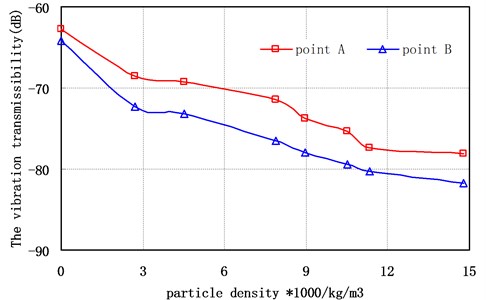
4.5. Particle density

Particle filling ratio is 70 %. Particle diameter is 0.5 mm. The vibration transmissibility of point A and point B of the offshore platform truss structure versus the particle density have shown in Fig. 14 and Fig. 15 respectively. They indicate that: (1) in the whole frequency range, with the increase of particle density, the vibration t transmissibility of the offshore platform truss structure has decreased, which mean that the greater the particle density the better the vibration reduction effect. (2) when the particle density is increased from 2200 to 7800 kg/m³, the particle density has a great influence on the vibration reduction effect. When the particle density reaches to certain level, the particle density has no obvious effect to the vibration reduction effect. (3) the vibration transmissibility of A and B measurement points with tungsten carbide particle damper have been reduced 10.5 dB and 9.5 dB respectively, compared with aluminum alloy particle damper. That indicates that it is important to choose the particle with large density as possible, in order to increase the vibration reduction effect.

Fig. 14Vibration transmissibility of the point A versus the particle density

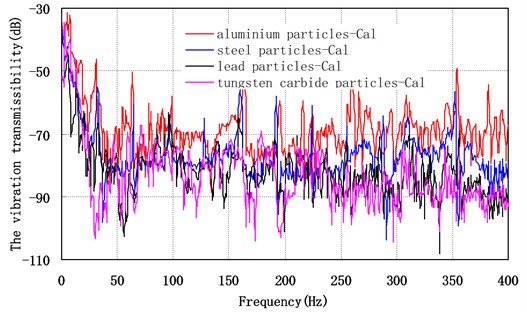
Fig. 15Vibration transfer rate of different measuring points versus density

5. Conclusions

This paper has used the finite element - discrete element simulation algorithm to study on the vibration characteristics of the offshore platform truss structure with semi-active particle damper. Some conclusions are made as follows:

1) The particle damping has an obvious effect of vibration reduction to the offshore platform truss structure, compared with the structure without particle damping. The vibration transmissibility has reduced 10.1 dB largest;

2) The effect of vibration reduction under revised on-off control strategy is better than that of on-off control strategy on the whole, but the effect of control strategy has difference on the vibration transmissibility at different measurement point. The vibration reduction effect of the offshore platform truss structure at under revised on-off control strategy and on-off control strategy have better effect compare with passive control on the whole, but the effect of vibration reduction is not obvious under semi-active control when the frequency less than 100 Hz.

3) The greater the particle density, the better the effect of vibration reduction, the vibration transmissibility with tungsten carbide particle damper has reduced 5.7 dB, compared with steel particle damper.

4) With the increase of the filling ratio, the vibration response of the offshore platform truss structure decreases first and then increases, and the offshore platform truss structure has the best effect of vibration reduction when the filling ratio is around 80 %. When the filling ratio is 100 %, the particle damper is still effective.

5) The effect of particle diameter is relatively low to the vibration reduction of platform truss structure. The average vibration transmissibility of the offshore platform truss structure with particle diameter 0.8 mm, 0.9 mm, 1.0 mm has reduced 2.3 dB, 3.1 dB, 3.8 dB respectively, compare with particle diameter 0.1 mm.

References

Zhang B. L., Tang G. Y. Active vibration H∞ control of offshore steel jacket platforms using delayed feedback. Journal of Sound and Vibration, Vol. 332, Issue 22, 2013, p. 5662-5677.

Publisher
Xia Z., Wang X., Hou J. Non-linear dynamic analysis of double-layer semi-active vibration isolation systems using revised Bingham model. Journal of Low Frequency Noise, Vibration and Active Control, Vol. 35, Issue 1, 2016, p. 17-24.

Publisher
Zhang B. L, Han Q. L. Network-based modelling and active control for offshore steel jacket platform with TMD mechanisms. Journal of Sound and Vibration, Vol. 333, Issue 25, 2014, p. 6796-6814.

Publisher
Li H., He X., Huo L. Seismic response control of offshore platform structures with shape memory alloy dampers. China Ocean Engineering, Vol. 19, Issue 2, 2005, p. 185-194.

Search CrossRef
Lei Y., Adhikari S., Friswell M. I. Vibration of nonlocal Kelvin-Voigt viscoelastic damped Timoshenko beams. International Journal of Engineering Science, Vol. 66, Issue 2, 2013, p. 1-13.

Publisher
Jiang J., Wang L., Yue H. H., et al. Vibration control of cylindrical shells with a hybrid photovoltaic/piezoelectric actuation mechanism. International Journal of Applied Electromagnetics and Mechanics, Vol. 46, Issue 4, 2014, p. 917-926.

Publisher
Bucci R. J., Mueller L. N., Vogelesang L. B., et al. Aluminium alloys-contemporary research and applications. Treatise on Materials Science and Technology, Vol. 174, Issue 3, 2007, p. 213-216.

Search CrossRef
Eldred L. B., Baker W. P., Palazotto A. N. Kelvin-Voigt versus fractional derivative model as constitutive relations for viscoelastic materials. AIAA Journal, Vol. 33, Issue 3, 2015, p. 547-550.

Publisher
Lu, Z., Lu X.,Masri S. F. Studies of the performance of particle dampers under dynamic loads. Journal of Sound and Vibration, Vol. 329, Issue 26, 2010, p. 5415-5433.

Publisher
Wang X., Liu X., Shan Y., et al. Design, simulation and experiment of particle dampers attached to a precision instrument in spacecraft. Journal of Vibroengineering, Vol. 17, Issue 4, 2015, p. 1606-1614.

Search CrossRef
Li K., Darby A. P. An experimental investigation into the use of a buffered impact damper. Journal of Sound and Vibration, Vol. 291, Issue 3, 2006, p. 844-860.

Publisher
Xia Z., Liu X., Shan Y. Application of particle damping for vibration attenuation in brake drum. International Journal of Vehicle Noise and Vibration, Vol. 7, Issue 2, 2011, p. 178-194.

Publisher
Lu Z., Lu X., Lu W., et al. Experimental studies of the effects of buffered particle dampers attached to a multi-degree-of-freedom system under dynamic loads. Journal of Sound and Vibration, Vol. 331, Issue 9, 2012, p. 2007-2022.

Publisher
Sánchez M., Pugnaloni, L. A. Effective mass overshoot in single degree of freedom mechanical systems with a particle damper. Journal of Sound and Vibration, Vol. 330, Issue 24, 2011, p. 5812-5819.

Publisher
Papalou A., Masri S. F. An experimental investigation of particle dampers under harmonic excitation. Journal of Vibration and Control, Vol. 4, Issue 4, 1998, p. 361-379.

Publisher
Michon G., Almajid A., Aridon G. Soft hollow particle damping identification in honeycomb structures. Journal of Sound and Vibration, Vol. 332, Issue 3, 2013, p. 536-544.

Publisher
Saeki M. Impact damping with granular materials in a horizontally vibrating system. Journal of Sound and Vibration, Vol. 251, Issue 1, 2002, p. 153-161.

Publisher
Wu C. J., Liao W. H., Wang M. Y. Modeling of granular particle damping using multiphase flow theory of gas-particle. Journal of Vibration and Acoustics, Vol. 126, Issue 2, 2004, p. 196-201.

Publisher
Masri S. F., Caughey T. K. On the stability of the impact damper. Journal of Applied Mechanics, Vol. 33, Issue 3, 1966, p. 586-592.

Publisher
Panossian H. V. Structural damping enhancement via non-obstructive particle damping technique. American Society of Mechanical Engineers Journal of Vibration and Acoustics, Vol. 114, 1992, p. 101-105.

Publisher
Sadek M. Impact dampers for controlling vibration in machine-tools. Machinery and Production Engineering, Vol. 120, Issue 3090, 1972, p. 152-161.

Search CrossRef
Els D. N. J. Damping of rotating beams with particle dampers: experimental analysis. AIAA Journal, Vol. 49, Issue 10, 2011, p. 2228-2238.

Publisher
Papalou A., Masri S. F. An experimental investigation of particle dampers under harmonic excitation. Journal of Vibration and Control, Vol. 4, Issue 4, 1998, p. 361-379.

Search CrossRef
Bryce L. F., Eric M. F., Steven E. O. Effectiveness and predictability of particle damping. SPIE’s 7th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, 2000.

Search CrossRef
Shah B. M., Nudell J. J., Kao K. R., et al. Semi-active particle-based damping systems controlled by magnetic fields. Journal of Sound and Vibration, Vol. 330, Issue 2, 2011, p. 182-193.

Publisher
He J. Z, Miao G. The interaction between two magnetic dipoles. Journal of Nanchang University, Vol. 18, Issue 3, 1996, p. 96-98, (in Chinese).

Search CrossRef

Cited by

Hysteretic behaviour and structural control performance of a piezoelectric friction damper

Xiaolong Zhang | Qixing Luo | Qinghua Han | Yan Lu | Yue Wang

(2023)

Research on Locally Resonant Characteristics of Pipelines with Periodic Structure

(2022)

A Critical Investigation of Force Transmissibility Characteristics in Various Isolator materials using Force Transmissibility Apparatus

Munish Baboria | Priya Devi

(2022)

An improved ESM-FEM method for seismic control of particle tuned mass damper in MDOF system

Kunjie Rong | Zheng Lu

(2021)

Vibration performance improvement of D/G-set employing inerter-rubber vibration isolator

Huabing Wen | Yang Li | Kun Zhang | Yue Liu | Chengwei Chang

(2021)

Sound radiation modes of cylindrical surfaces and their application to vibro-acoustics analysis of cylindrical shells

Yao Sun | Tiejun Yang | Yuehua Chen

(2018)

The transmissibility of a vibration isolation system with ball-screw inerter based on complex mass

Huabing Wen | Junhua Guo | Yang Li | Yue Liu | Kun Zhang

(2018)

Discrete Near-Optimal Wave Disturbances Rejection Control for Offshore Platforms With Delays in Measurement and Actuator

Yong-Zheng Lin | Hong Liu | Zhen-Xiang Chen

(2018)

Identification and contribution analysis of vehicle interior noise based on acoustic array technology

Bao Guozhi | Shao Guangsheng | Xia Zhaowang | Den Jianghua

(2017)

About this article

Received

04 July 2016

Accepted

06 September 2016

Published

15 November 2016

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2016.17365

Keywords

semi-active particle damping

control strategy

offshore platform

coupling simulation algorithm

Acknowledgements

The research work reported in this paper was sponsored by the National Science Foundation of China (11302088), the Natural Science Foundation of Jiangsu Province (BK2012278), and the Natural Science Foundation of Colleges of Jiangsu Province (16KJB580002).

Author Contributions

Zhaowang Xia developed the coupling simulation algorithm for semi-active particle damper. Kaijie Mao designed the semi-active particle damper. Xuetao Wang and Guangsheng Shao designed experimental setup of the offshore platform truss structure. Wenan Jiang studied the influence of control strategy and key parameters of semi-active particle damping on the vibration reduction effect of the offshore platform truss structure. Yao Sun developed the on-off control strategy and revised on-off control strategy for semi-active particle damper.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 12 15

PSO optimum control strategy of 7 degrees of freedom semi-active suspensions

Jubin Qiao, Yeonsung Choi, Fuqiang Yang

Research article

2018 12 31

Optimization design of semi-active controller for in-wheel motors suspension

Fangwu Ma, Jiawei Wang, Yang Wang, Longfan Yang

Research article

2018 09 30

The optimal control of semi-active suspension based on improved particle swarm optimization

Haijing Yan, Jubin Qiao, Sen Zhang, Ting Zhao, Zhongchang Wang

Review article

2017 08 15

Invited Review: Recent developments in vibration control of building and bridge structures

Khaled Ghaedi, Zainah Ibrahim, Hojjat Adeli, Ahad Javanmardi

Z. Xia, J. Kai, X. Wang, G. Shao, W. Jiang, and Y. Sun, “Study on semi-active particle damping technology for offshore platform truss structure,” Journal of Vibroengineering, Vol. 18, No. 7, pp. 4248–4260, Nov. 2016, https://doi.org/10.21595/jve.2016.17365

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.17365
UR  - https://doi.org/10.21595/jve.2016.17365
TI  - Study on semi-active particle damping technology for offshore platform truss structure
T2  - Journal of Vibroengineering
AU  - Sun, Yao
AU  - Xia, Zhaowang
AU  - Kai, Jiemao
AU  - Wang, Xuetao
AU  - Shao, Guangsheng
AU  - Jiang, Wenan
PY  - 2016
DA  - 2016/11/15
PB  - JVE International Ltd.
SP  - 4248-4260
IS  - 7
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Sun_2016,
	doi = {10.21595/jve.2016.17365},
	url = {https://doi.org/10.21595/jve.2016.17365},
	year = 2016,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {7},
	pages = {4248--4260},
	author = {Yao Sun and Zhaowang Xia and Jiemao Kai and Xuetao Wang and Guangsheng Shao and Wenan Jiang},
	title = {Study on semi-active particle damping technology for offshore platform truss structure},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Y. Sun, Z. Xia, J. Kai, X. Wang, G. Shao, and W. Jiang, “Study on semi-active particle damping technology for offshore platform truss structure,” Journal of Vibroengineering, vol. 18, no. 7, pp. 4248–4260, Nov. 2016, doi: 10.21595/jve.2016.17365.

Copy IEEE

Copied to clipboard!

Sun, Yao, Zhaowang Xia, Jiemao Kai, Xuetao Wang, Guangsheng Shao, and Wenan Jiang. “Study on Semi-Active Particle Damping Technology for Offshore Platform Truss Structure.” Journal of Vibroengineering 18, no. 7 (November 15, 2016): 4248–60. https://doi.org/10.21595/jve.2016.17365.

Copy Chicago

Copied to clipboard!

Study on semi-active particle damping technology for offshore platform truss structure

Abstract

1. Introduction

2. Coupling simulation algorithm

2.1. The contact force and magnetic force

2.2. Semi-active control strategy

2.2.1. On-off control strategy

2.2.2. Revised on-off control strategy

2.3. Description of motion

3. Experimental results

3.1. Experimental setup

4. The effect of parameters to the vibration characteristics of the offshore platform truss structure with semi-active particle damper

4.1. Control current

4.2. Control strategy

4.3. Particle diameter

4.4. Filling ratio

4.5. Particle density

5. Conclusions

References

Cited by

About this article

Related Articles