Abstract
This paper presents a state-of-the-art review of recent articles published on active, passive, semi-active and hybrid vibration control systems for structures under dynamic loadings primarily since 2013. Active control systems include active mass dampers, active tuned mass dampers, distributed mass dampers, and active tendon control. Passive systems include tuned mass dampers (TMD), particle TMD, tuned liquid particle damper, tuned liquid column damper (TLCD), eddy-current TMD, tuned mass generator, tuned-inerter dampers, magnetic negative stiffness device, resetting passive stiffness damper, re-entering shape memory alloy damper, viscous wall dampers, viscoelastic dampers, and friction dampers. Semi-active systems include tuned liquid damper with floating roof, resettable variable stiffness TMD, variable friction dampers, semi-active TMD, magnetorheological dampers, leverage-type stiffness controllable mass damper, semi-active friction tendon. Hybrid systems include shape memory alloys-liquid column damper, shape memory alloy-based damper, and TMD-high damping rubber.
1. Introduction
Main Control has been a key technology in many fields such as vehicle engineering [1], manufacturing [2, 3], and robotics [4, 5]. Many articles have recently been published about vibration control of structures subjected to dynamic loading such as strong ground motions. Fisco and Adeli [6] brought forward a state-of-the-art review of active control of structures including active tuned mass dampers (ATMD), active tendon systems, active magnetorheological (MR) dampers, distributed actuators, piezoelectric dampers (PDs), semi-active stiffness dampers (SASD) and semi-active tuned liquid column dampers up to 2010. Fisco and Adeli [7] reviewed hybrid vibration control systems including actuators with passive dampers, hybrid mass dampers, semi-active base isolators, and semi-active TLCDs with passive dampers with emphasis on implementation of practical and robust control algorithms such as Linear-Quadratic-Regulator (LQR) and linear-quadratic-Gaussian technique [8-11], sliding mode (Yeganeh-Fallah and Taghikhany, 2016), neural network-based approach [12, 13], wavelet-based structural control algorithm introduced for the first time by [14-16], and fuzzy logic (FL) controllers [17-20] to find the magnitudes of the actuator forces. Korkmaz [21] presented a review of active vibration control (AVC) systems in structures including active cable and tendon control, active strut control, aerodynamic appendages and ATMDs using different control algorithms applied to actuators and sensors. Khoury and Adeli [22] presented a review of journal articles on vibration control of structures under dynamic loads including ATMD, piezoelectric actuators (PA) in the active system category, and TLCD, pendulum TLCD, circular TLCD and Tuned liquid column ball damper in the passive vibration category. Other systems reviewed include the negative stiffness devices (NSD), semi-active TMD (STMD), variable stiffness STMD, MR dampers, MR-TMD and re-centring variable friction damper in the semi-active system category, and finally semi-active MR dampers with nonlinear base isolators and active base isolation systems in the hybrid system category. Gutierrez Soto and Adeli [23] presented a review of different placements of active, passive, semi-active and hybrid vibration control dampers in civil structures under different dynamic excitations. Basu et al. [24] reviewed the applications of vibration control systems for buildings, bridges, and wind turbines across Europe, up to 2013, considering active, passive and semi-active dampers as well as functional materials and their performance. Gutierrez Soto and Adeli [25] presented a review of TMDs classified into four main categories: conventional TMDs, bidirectional TMDs, TLCD and pendulum TMDs.
It can be seen from the aforementioned articles that the field of structural vibration control is a very active area of research. This paper is a state-of-the-art review of recent articles published on active, passive, semi-active and hybrid vibration control systems for structures under dynamic loadings primarily since 2013.
2. Structural control systems
Structural control systems are used to decrease vibrational responses of structures due to various sorts of dynamic loadings such as traffic, winds, and earthquakes. Investigations of the structural vibration control have escalated since 1980s and a large number of methods and devices have been proposed and classified into active, passive and semi-active control systems.
2.1. Active vibration control (AVC)
In an AVC system, the essential information of structural behaviour under dynamic loading is received by a controller through sensors, and actuators generate control forces to counter external motions [16, 26] (Fig. 1).
Fig. 1AVC Configuration
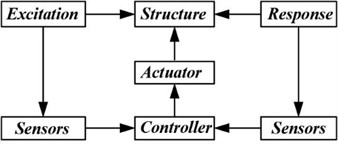
2.1.1. AVC in buildings
In recent years, notable attempts have been devoted to the advancement of the active mass dampers (AMD), active tuned mass dampers (ATMD), active tendon control (ATC), and distributed mass damper (DMD) vibration control systems in order to enhance serviceability and reduce the dynamic responses of civil engineering structures subjected to environmental loads such as wind and ground excitations. Nigdeli and Boduroğlu [27] controlled torsionally irregular structures subjected to near-fault ground excitation through ATC. A numerical algorithm that scans the peak responses in the time-domain for arrangements of control coefficients was used to tune proportional-integral-derivative (PID) parameters. It was shown the ATC system was effective for mitigation of maximum responses and obtaining a swift steady-state response.
Amini et al. [28] discussed approaches for determining optimal control forces of ATMD using particle swarm optimization [29, 30], discrete wavelet transform (DWT) [31, 32], and LQR algorithm. After testing the method on a 10-story building subjected to near-fault motions, the results showed that, the proposed approach was effective to reduce the displacement response in real time. Soleymani and Khodadadi [33] introduced an ATMD for vibration control of a 76-story building under both seismic and wind motions. A multiobjective genetic-fuzzy algorithm [20] and an adaptive switching-type fuzzy controller were used to enhance the ATMD performance under dynamic excitations. Tinkir et al. [34] presented experimental results for deflection control of a 2-DOF structure subjected to a scaled earthquake using proportional-integral (PI) controlled AMD system. Wang and Adeli [35] presented a filtered sliding mode control method to reduce the wind-induced response of high-rise buildings and applied it to a 76-story building using an ATMD installed on the roof. Ubertini et al. [36] used a sky-hook control algorithm on a proposed AMD system installed on the top floor of a scaled 5-story steel structure. The AMD is made up of an electric torsional servomotor, a ball screw, a potentiometer and additional carried mass as displayed in Fig. 2. Yang et al. [37] proposed a multi-modal negative acceleration feedback control algorithm for an AMD system activated by an AC servomotor connected to a portable mass through a ball-screw mechanism where an accelerometer is used as a sensor to measure vibrations.
Fig. 2Components of ball screw used by Ubertini et al. [36]
![Components of ball screw used by Ubertini et al. [36]](https://static-01.extrica.com/articles/18900/18900-img2.jpg)
Teng et al. [38] performed influence time delay analysis on stability and system poles in order to decrease the effect of time delay on the AMD control systems. To ensure the stability of the system, a formula for the maximum time-delay was established. Fu et al. [39] analysed active control techniques for a DMD system to demonstrate structural response mitigations. A 20-story building equipped with 20 DMDs was utilized as a test-bed. Authors report the active DMD performs better than the standard active control systems whilst utilizing similar amount of energy.
Amini and Samani [40] suggested a time-varying wavelet-based pole assignment (WPA) controller to reduce seismic vibrations in MDOF structures. The discrete wavelet transform (DWT) was implemented to specify the energy amount of the structural response in real time in a frequency band where the frequency was used in the Big Bang–Big Crunch algorithm to update adaptively the optimal values of the closed loop poles of the system. The proposed WPA method was experimentally verified on a 10-story building system, and also through numerical examples under several excitations. Yanik et al. [41] proposed an AVC performance index considering the mechanical energy minimization of a 3D 6-story building, seismic energies and their control using a fully active tendon system designed by a linear optimal control algorithm. No request to solve the nonlinear Riccati equation [9] was noted as the advantage of the control system. Omidi et al. [42] presented Multi Positive Feedback (MPF) control for mitigation of active vibration in piezoelectric-actuated flexible smart structures. The MPF was designed in order to control concurrently the vibrations of single and multi-resonant frequency.
Nazarimofrad and Zahrai [43] developed a mathematical model to control the behaviour of irregular buildings subjected to earthquakes by means of active tendons using the LQR algorithm taking into account the soil-structure interaction effect. Liu et al. [44] proposed a multiple source multiple harmonic active vibration suppression algorithm considering feedforward structure accordance with conjugate gradient method and reference amplitude rectification. A finite element model in-loop simulation (FEMILS) was also presented for quick algorithm validation. Yavuz et al. [45] present a closed loop control technique for active vibration suppression of the vibrations of a 4-DOF system. The PID control algorithm was applied to detect the error signal value of actuator in each time step. Bakule et al. [46] presented decentralized networked vibration control of building structures.
2.1.2. AVC in bridges
Inordinate and unforeseen cable vibration of bridges is deleterious for the long-term serviceability and safety of bridge structures [47]. It may cause premature failure of connections as a result of fatigue or collapse of cable-corrosion-protection systems. Furthermore, vibration of stay cables will decrease public confidence. To eliminate or reduce destructive vibration of cable-stayed bridges, application of supplementary devices installed close to the cable anchorages has been used for quite some time. More recently, control strategies have been proposed to actively suppress vibrations of cables.
Kim and Adeli [48] presented a wavelet hybrid feedback-linear mean squared algorithm for vibration control of cable-stayed bridges. Pereira et al. [49] proposed an active vibration control methodology to control human vibrations on pedestrian bridges based on Multi-Input Multi-Output vibration control.
Most structural control papers assume linear structural behavior. Wang and Adeli [50] introduced a novel self-constructing wavelet neural network algorithm for nonlinear control of large structures using an adaptive fuzzy sliding mode control approach. The authors note “The algorithm is particularly suitable when the physical properties such as the stiffnesses and damping ratios of the structural system are unknown or partially known which is the case when a structure is subjected to an extreme dynamic event such as an earthquake as the structural properties change during the event.” The method was used for mitigation of vibration response of a continuous pre-stressed concrete box girder bridge subjected to dynamic excitations.
Integration of the three main fields of computational intelligence, that is, neural networks, genetic algorithm, and fuzzy logic for solution of complicated pattern recognition problems was advanced in a seminal book by Adeli and Hung [51]. Mitchell et al. [52] presented a wavelet-filtered genetic neuro-fuzzy system using aspects of DWTs, Implicit Redundant Representation, Evolutionary Genetic Algorithm (GA) [53, 54], neural networks, and FL [55, 56] to control motions of highway bridges under different seismic loadings.
2.2. Passive vibration control (PVC)
In contrast to AVC, PVC systems are not operated by any external force or source. In the passive control approach, control devices are embedded or connected to the structural members (Fig. 3) to improve the structural damping or increase the stiffness without any use of external force.
Fig. 3Components of a PVC

2.2.1. PVC in buildings
Many investigators have studied the effectiveness and advantages of TMDs and have introduced different approaches to improve their robustness and effectiveness. Bekdaş and Nigdeli [57] used a Harmony Search algorithm [58, 59] to determine the TMD optimum parameters including damping ratios, frequency and TMD mass.
The inerter system has been used earlier in vibration control through base isolation systems. Recently, Lazar et al. [60] analysed the feasibility of a Tuned-Inerter Damper control approach as a substitute for TMDs. Marian and Giaralis [61] proposed a passive device, known as TMD-inerter (TMDI) compounding the conventional TMD with an inerter device. The inerter in the introduced TMDI configuration provides a “mass amplification effect” as a supplementary connective part between the ground and the TMD pendulous mass for an SDOF, and between the primary structure and TMD pendulous mass for chain-like MDOF primary structures. Jin et al. [62] introduced two configurations of inerter-based passive vibration controls, namely a mass linked to a parallel damper and spring in series with an inerter (Case 1), and a traditional dynamic vibration absorber in series with an inerter (Case 2) for vibration control of the beam-type structures (Fig. 4). The comparison between Case 1 and Case 2 illustrated that for a larger mass ratio Case 2 had better performance than Case 1 while the opposite was true for a smaller mass ratio. In the commonly-used laminated steel/rubber isolation bearings, a high vertical stiffness is created by the steel shims, whereas the rubber sheets secure horizontal flexibility. This form of Base Isolators (Bis) is big, weighty, and often costly. To overcome the problem, Tan et al. [63] proposed a cost-effective and light isolator for low-rise building structures, made of plastic shims and unsaturated Fibre Reinforced Polyester (FRP) used between rubber layers.
A particle damper (PD) consists of mass particles placed in a container. Once the structure vibrates, the particles play opposite to the structure (primary system) movement and hit the container walls; switching momentum and alleviating the primary system response. Papalou and Strepelias [64] investigated a technique to support multi-drum ancient columns using PD. The proposed method introduced the utilization of PDs in the form of traditional drums having a hollow section encompassing particles.
Fig. 4Two configurations of inerter-based passive vibration control: a) a mass linked to a parallel damper and spring in series with an inerter (Case 1), b) a traditional dynamic vibration absorber in series with an inerter (Case 2) for vibration control of the beam-type structures proposed by Jin et al. [62]
![Two configurations of inerter-based passive vibration control: a) a mass linked to a parallel damper and spring in series with an inerter (Case 1), b) a traditional dynamic vibration absorber in series with an inerter (Case 2) for vibration control of the beam-type structures proposed by Jin et al. [62]](https://static-01.extrica.com/articles/18900/18900-img4.jpg)
![Two configurations of inerter-based passive vibration control: a) a mass linked to a parallel damper and spring in series with an inerter (Case 1), b) a traditional dynamic vibration absorber in series with an inerter (Case 2) for vibration control of the beam-type structures proposed by Jin et al. [62]](https://static-01.extrica.com/articles/18900/18900-img5.jpg)
Dai et al. [65] presented a passive vibration control device, Tuned Liquid Particle Damper (TLPD), which integrates the conventional TLD and PD features as demonstrated in Fig. 5. The nonlinear performance of the TLPD was investigated by installing it in a 5‐story steel frame building subjected to dynamic motions. Ruiz et al. [66] proposed a TLD with Floating Roof (TLD-FR) as shown in Fig. 6, to avoid wave breaking phenomena. A supplemental damping system was also considered for the TLD-FR like viscous damper (VD) to enhance the optimal damping for the shaken liquid. Lu et al. [67] proposed a particle TMD based on the synthesis of the particle dampers and TMDs.
Fig. 5Scheme of tuned liquid particle damper [65]
![Scheme of tuned liquid particle damper [65]](https://static-01.extrica.com/articles/18900/18900-img6.jpg)
Fig. 6TLD-FR [66]
![TLD-FR [66]](https://static-01.extrica.com/articles/18900/18900-img7.jpg)
Min et al. [68] presented a two-way liquid damper using a combination of TLCD and Tuned Sloshing Damper on a 64-story building structure. Hejazi et al. [69] proposed a multi-objective optimization technique using GA [70, 71] to modify the performance of passive devices in order to reduce the damage response of structural members as well as story displacements. Hejazi et al. [72] presented a finite element-based analytical model as well as a constitutive law for viscous wall dampers for RC structures subjected to seismic loading.
Energy dissipating devices made of metals such as steel, Shape Memory Alloys (SMAs), lead, and copper have been used to mitigate the seismic response of structures successfully. Qian et al. [73] proposed a re-centring SMA damper using nitinol wires as a superelastic components to dissipate energy as indicated in Fig. 7. Briones and de la Llera [74] presented a copper-based bidirectional energy dissipation damper where the device cyclic response demonstrated that the damper has a good deformation capacity to dissipate energy before failure.
Walsh et al. [75] presented a resetting passive stiffness damper (RPSD) in line with modification of resetting semi-active stiffness damper (RSASD) where the feedback components of RSASD were substituted by a rack-lever mechanism, as illustrated in Fig. 8, to attain damper resetting as a function of the applied force.
Fig. 7Re-centring SMA damper using nitinol wires proposed by Qian et al. [73]
![Re-centring SMA damper using nitinol wires proposed by Qian et al. [73]](https://static-01.extrica.com/articles/18900/18900-img8.jpg)
Fig. 8RPSD configuration using the rack-lever mechanism presented by Walsh et al. [75]
![RPSD configuration using the rack-lever mechanism presented by Walsh et al. [75]](https://static-01.extrica.com/articles/18900/18900-img9.jpg)
Viscoelastic passive energy dissipation devices have been used as effective tools for earthquake-induced vibration control in buildings. Yamamoto and Sone [76] proposed a combination use of metallic yielding component with viscoelastic damper installed in three different frame systems.
Shi and Zhu [77] presented two schemes of passive NSDs by means of magnetism, called Magnetic Negative Stiffness Dampers, composed of a number of constant magnets set into a conductive pipe as shown in Fig. 9. The proof of concept laboratory tests were conducted on an MTS machine where a cyclic displacement was applied to the prototype.
Fig. 9Two different types of magnetic negative stiffness dampers composed of a number of constant magnets set into a conductive pipe proposed by Shi and Zhu [77]
![Two different types of magnetic negative stiffness dampers composed of a number of constant magnets set into a conductive pipe proposed by Shi and Zhu [77]](https://static-01.extrica.com/articles/18900/18900-img10.jpg)
![Two different types of magnetic negative stiffness dampers composed of a number of constant magnets set into a conductive pipe proposed by Shi and Zhu [77]](https://static-01.extrica.com/articles/18900/18900-img11.jpg)
2.2.2. PVC in bridges
Applications of passive control systems in bridge engineering has attracted many attentions in terms of proposing innovative control devices. Passive control systems have proven to be effective in reducing the cable vibrations as the control system can be adjusted for maximum damping ratio. Yan et al. [78] showed the usefulness of tuned particle dampers on a scaled model of a continuous viaduct subjected to ground motions. Miguel et al. [79] suggested concurrent optimization of placement and force of friction dampers (FDs) using the Firefly Algorithm [80]. They evaluated the proposal on two footbridges under human-induced vibrations where locations and forces of FDs were the design variables. Takeya et al. [81] introduced an energy harvester device known as Tuned Mass Generator (TMG) consisting of a tuned dual-mass damper system for vibration control of bridges. An electromagnetic transducer was applied to use the unused energy reserve of the damper. Moreover, TMG was tuned through multi-domain parameter design approach for both the power generation and energy storage. Miguel et al. [82] presented an application of robust optimal design (ROD) of TMD and Multiple-TMD for vehicle-induced vibration of bridges by implementation of a parallel-processing Monte Carlo simulation to carry out the high computational complexity.
Camara et al. [83] proposed an approach to design optimum yielding dampers employing Triangular Added Damping and Stiffness (TADAS) dampers placed between the deck and supports, based on the equivalent SDOF approximation for short to medium span cable-stayed bridges in the transverse direction. Attary et al. [84, 85] evaluated the performance of Negative Stiffness Devices (NSD) for seismic response control of scaled highway bridge structures experimentally on a shake table using four different bridge configurations: 1) isolated bridge (IB); 2) NSDs+IB; 3) VD+IB; and 4) NSDs+VD+IB. The proposed NSD is shown in Fig. 10.
Fig. 10Negative stiffness device (NSD) investigated by Attary et al. [84]
![Negative stiffness device (NSD) investigated by Attary et al. [84]](https://static-01.extrica.com/articles/18900/18900-img12.jpg)
2.3. Semi-active vibration control (SVC)
A semi-active device is usually defined as an active device with small energy requirement such as that of a battery. As such, an advantage of this system is providing protection when the power sources fail under extreme excitations, unlike an entirely active system.
2.3.1. SVC in buildings
One of the most prevalent SVC systems is the MR damper which uses magnetorheological fluids to provide adaptable damping. The MR damper has been considered widely in vibration control of both buildings and bridges. Zeinali et al. [86] employed an Adaptive Neuro-Fuzzy Inference System (ANFIS) to investigate a phenomenological dynamic model of two types of MR dampers, a short and a long stroke damper, used in laboratory tests. Cha et al. [87] performed hybrid simulations of 200-kN MR dampers in moment-resisting frames subjected to earthquake excitations using four control algorithms including clipped optimal, Lyapunov stability-based, and decentralized output feedback polynomial control algorithms. Khalid et al. [88] examined a reduced-scale MR damper model considering the valve mode mechanism through recurrent neural network (RNN) [89] approach for rehabilitation of the nonlinear hysteretic behavior of MR dampers. Xu et al. [90] integrated the back-propagation (BP) with Artificial Bee Colony (ABC) algorithm, called ABC BP-ANN, to find the required voltage of MR dampers.
Semi-active TMD (STMD) has been developed as an appealing alternative to conventional TMDs with the advantage of being robust to changes in the damping and stiffnesses of the associated structures. Lin et al. [91] proposed a semi-active resettable variable stiffness TMD (RVS-TMD) to improve the TMD control performance. It consists of an RVS damper which includes a control stiffness element, a resettable element, and an undamped TMD system as shown in Fig. 11. Chu et al. [92] introduced a leverage-type stiffness controllable mass damper as a semi-active vibration control system to improve the conventional TMD performance. It consists of a leverage arm with a portable pivot, allowing to change the lever arm by changing the position of the pivot to restore the force in real time and control the stiffness of the damper as shown in Fig. 12.
Fig. 11Schematic diagram of RVS-TMD proposed by Lin et al. [91]
![Schematic diagram of RVS-TMD proposed by Lin et al. [91]](https://static-01.extrica.com/articles/18900/18900-img13.jpg)
Fig. 12Leverage-type stiffness controllable mass damper [92]
![Leverage-type stiffness controllable mass damper [92]](https://static-01.extrica.com/articles/18900/18900-img14.jpg)
Piezoelectric friction dampers (PFD) are classified as adaptive/intelligent systems. Etedali et al. [93] discussed optimal PID controllers for isolated buildings equipped with PFDs as a semi-active control system. Variable friction dampers (VFD) are another solution for structural vibration control capable of high-energy dissipation by converting mechanical energy into heat through friction mechanism controllable via an actuator. Cao et al. [94] proposed a semi-active VFD based on the duo-servo drum brake technology of vehicles. To evaluate the damper, they fabricated a scaled-down prototype and characterized its dynamic performance. Garrido et al. [95] studied a semi-active friction tendon using two different control laws: simplified quickest-descent control law based on the velocity-feedback and Slackening-Preventing Control Law based on the force-feedback for vibration control of buildings and bridges.
Shi et al. [96] presented a semi active floor isolation scheme to decrease displacement and acceleration of buildings under both long- and short-period excitations by adapting the LQR control algorithm through frequency-dependent scheduled gain (Fig. 13). Qu et al. [97] introduced a method to optimize the negative stiffness and additional damping values in different floors of a building by means of the decentralized-static-feedback controller and the homotopy procedure and applied it to a 20-story benchmark building structure.
Fig. 13Semi active floor isolation scheme proposed by Shi et al. [96]
![Semi active floor isolation scheme proposed by Shi et al. [96]](https://static-01.extrica.com/articles/18900/18900-img15.jpg)
2.3.2. SVC in bridges
MR dampers have been used as a popular solution for vibration control of cables in bridge structures because of their real-time tuning ability. Luu et al. [98] investigated the vibration control of railway bridges in the transverse direction subjected to high-speed traffic through MR dampers (Fig. 14). An H∞ algorithm was derived to control damping forces of the MR damper and the ANFIS technique was used to predict voltages of the MR damper.
Weber [99] presented a semi-active vibration absorber (SVA) using a rotational MR damper (Fig. 15), known as MR-SVA, to reduce the vibrations of a bridge tested at Empa (Swiss Federal Laboratories for Materials Science and Technology) where the passive absorbers of the MR-SVA are properly adjusted to the target resonance frequency of the bridge.
Fig. 14Vibration control of railway bridges in the transverse direction subjected to high-speed traffic through MR dampers [98]
![Vibration control of railway bridges in the transverse direction subjected to high-speed traffic through MR dampers [98]](https://static-01.extrica.com/articles/18900/18900-img16.jpg)
Chen et al. [100] exhibited a self-sensing MR damper for protection of bridge stay cables under extreme vibrations using the linear-quadratic-Gaussian control strategy and a Bayesian NARX network approach taking into consideration the limited measurements and a collocated sensing-damping arrangement as well as nonlinear dynamics of the self-sensing damper. Heo et al. [101] proposed an MR damper with a lumped mass in a two-span bridge to reduce its longitudinal vibration under near- and far-field earthquakes.
To mitigate vibration response of the bridges, a few other devices and control approaches have been developed. Andersson et al. [102] studied external damper systems to mitigate the vibration of a railway bridge and developed procedures for a variable stiffness semi-active TMD by means of tuning frequencies. Electromagnetic dampers (EMD) are another type of dampers that can generate electrical energy from kinetic energy over electromagnetic infusion. Shen and Zhu [103] presented an EMD cum-energy-harvester consisting of an electromagnetic device attached to a circuit. The proposed damper was tested on a scaled cable-stayed bridge.
Fig. 15Semi-active vibration absorber using a rotational MR damper [99]
![Semi-active vibration absorber using a rotational MR damper [99]](https://static-01.extrica.com/articles/18900/18900-img17.jpg)
Fig. 16Components of an HVC system
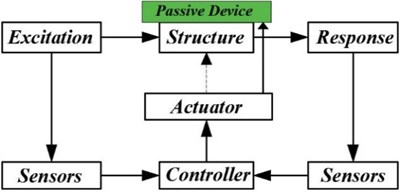
2.4. Hybrid vibration control (HVC)
An HVC system is usually a combination of active, semi-active and passive vibration control systems with two distinct advantages: it provides redundancy and it needs less energy (Fig. 16).
2.4.1. HVC in buildings
Liquid Column Dampers (LCDs) have been used successfully for vibration control of flexible structures. Tuning LCDs for short-period structures is not convenient. Several alterations have been proposed on the primary LCD structure to improve its workability in relatively stiff structures. Gur et al. [104] showed that the efficacy of the LCD for vibration control of short-period structures can be enhanced by substituting a linear spring with SMA material, called SMA-LCD. The SMA-LCD system consists of an LCD connected to the main structure through an SMA spring as shown in Fig. 17, where and are the damping and mass of the SDOF structure, and , and are the vertical displacement of the liquid column, liquid container displacement relative to the SDOF system and the displacement of the structure relative to the ground, respectively.
Hogsberg and Brodersen [105] presented a hybrid system consisting of a passive dashpot placed in series with a load cell to measure the damper force and an active actuator. A filtered Integral Force Feedback approach was used to control the actuator motion. Jalaeefar and Asgarian [106] also presented a hybrid shape memory alloy-based damper which combines strain recovering and energy dissipation. The system was recommended for semi-rigid braced frames.
Fig. 17SMA-LCD in a SDOF system proposed by Gur et al. [104]
![SMA-LCD in a SDOF system proposed by Gur et al. [104]](https://static-01.extrica.com/articles/18900/18900-img19.jpg)
2.4.2. HVC in bridges
Cu and Han [107] introduced a combination of a TMD with a viscous damper to reduce unfavourable vibrations of taut cables of the cable-stayed bridges and stadiums. Recently, Cu et al. [108] proposed a similar idea of combining a TMD with high damping rubber.
2.5. Hybrid base isolation (BI) systems
Several hundred buildings and bridges in seismic regions have been equipped with base isolation systems in the past few decades. A problem with BIs is large movements at the base level that need to be reduced. To deal with this issue, researchers have proposed hybrid base isolation systems. Pham and Ahn [109] presented Horizontal Active Vibration Isolator (HAVI) using forces of an EM Planar Actuator (EPA) in both vertical and horizontal directions. The vertical force was utilized to adjust the natural frequency of the isolator, whereas the horizontal force was applied to reduce the horizontal disturbance of the isolator. A model of the HAVI was simulated using Flexible Beam Column (FBC), as shown in Fig. 18, and the efficiency of the proposed isolator was tested through an experimental study.
Fig. 18HAVI scheme [109]
![HAVI scheme [109]](https://static-01.extrica.com/articles/18900/18900-img20.jpg)
Liu et al. [110] suggested a hybrid isolator using an X-shape supporting structure. The hybrid isolator combined the advantageous aspects of both the scissor-like and lever-type structures to obtain an ultra-low frequency from the isolator. Huang et al. [111] introduced a structured passive isolator made of a mechanical spring to provide positive stiffness and a knife-edge supports to act as a slit for placement of a sliding beam as shown in Fig. 19. It was demonstrated that by providing negative stiffness the hybrid isolator could attain remarkable ultra-low frequency and prominently, the system could recognize a uniformly low broadband vibration transmissibility that had never been addressed before.
Wu et al. [112] proposed an isolator utilizing a magnetic spring (MS) with NS, called MS-NS, plus a positive stiffness (PS) spring used in parallel. The PS spring consists of two flexible hinges and a coil spring. The MS-NS consists of three cubical magnets arranged in repulsive mode to provide negative stiffness as shown in Fig. 20. The MS-NS can decrease the isolator natural frequency.
Calvi et al. [113] introduced two variable friction bearings, made of three sliding surfaces with different frictional materials to identify the basic differences between constant friction and variable friction sliding isolators. Chen and Liang [114] offered an AVC method to boost the performance of a pneumatic isolation system in the low-frequency range. It consists of a pneumatic cylinder, a rubber shutter and a piston to support a payload mass. The method applied an adaptive Wavelet Neural Network (WNN) algorithm [16] to capture the time varying characteristics of nonlinear system as well as to nullify the response payload.
Fig. 19Proposed base isolator by [111]
![Proposed base isolator by [111]](https://static-01.extrica.com/articles/18900/18900-img21.jpg)
Fig. 20Configuration of the proposed vibration isolator [112]
![Configuration of the proposed vibration isolator [112]](https://static-01.extrica.com/articles/18900/18900-img22.jpg)
3. Concluding remarks
It is observed from the reviewed literature that significant research has been conducted on the design, development, and verification of novel earthquake-resistant systems for improving seismic performance of building and bridge structures. Passive control systems nowadays are well-accepted, although they are characteristically tuned to particular dynamic motions and their effectiveness is bandwidth-limited. Active and especially semi-active control systems have also received much attention during recent years with numerous control methods to improve their performances under dynamic excitations. In addition, hybrid designs using different techniques in terms of combining characteristics of damping materials as well as structural systems have been advanced. It can be concluded that developments in the structural vibration control area will continue to grow because of advances in new materials, sensors, and computing and information technologies.
References
-
Wang J.-Q., Li S. E., Zheng Y., Lu X.-Y. Longitudinal collision mitigation via coordinated braking of multiple vehicles using model predictive control. Integrated Computer-Aided Engineering, Vol. 22, Issue 2, 2015, p. 171-185.
-
Li Y., Liu C., Gao J. X., Shen W. An integrated feature-based dynamic control system for on-line machining, inspection and monitoring. Integrated Computer-Aided Engineering, Vol. 22, Issue 2, 2015, p. 187-200.
-
Guzman C., Castejon P., Onaindia E., Frank J. Reactive execution for solving plan failures in planning control applications. Integrated Computer-Aided Engineering, Vol. 22, Issue 4, 2015, p. 343-360.
-
Wang X., Zhang G., Neri F., Jiang T., Zhao J., Gheorghe M., Ipate F., Lefticaru R. Design and implementation of membrane controllers for trajectory tracking of nonholonomic wheeled mobile robots. Integrated Computer-Aided Engineering, Vol. 23, Issue 1, 2016, p. 15-30.
-
Abdul Ghani N. M., Tokhi M. O. Simulation and control of multipurpose wheelchair for disabled/elderly mobility. Integrated Computer-Aided Engineering, Vol. 23, Issue 4, 2016, p. 331-347.
-
Fisco N. R., Adeli H. Smart structures: Part I – Active and semi-active control. Scientia Iranica, Vol. 18, Issue 3, 2011, p. 275-284.
-
Fisco N. R., Adeli H. Smart structures: Part II – Hybrid control systems and control strategies. Scientia Iranica, Vol. 18, Issue 3, 2011, p. 285-295.
-
Lu L.-T., Chiang W.-L., Tang J.-P. LQG/LTR control methodology in active structural control. Journal of Engineering Mechanics, Vol. 124, Issue 4, 1998, p. 446-454.
-
Adeli H., Saleh A. Optimal control of adaptive/smart bridge structures. Journal of Structural Engineering, Vol. 123, Issue 2, 1997, p. 218-226.
-
Ma T.-W., Yang H. T. Y. Adaptive feedback-feedforward control of building structures. Journal of Engineering Mechanics, Vol. 130, Issue 7, 2004, p. 786-793.
-
Djajakesukma S. L., Samali B., Nguyen H. Study of a semi-active stiffness damper under various earthquake inputs. Earthquake Engineering and Structural Dynamics, Vol. 31, Issue 10, 2002, p. 1757-1776.
-
Hung S.-L., Kao C. Y., Lee J. C. Active pulse structural control using artificial neural networks. Journal of Engineering Mechanics, Vol. 126, Issue 8, 2000, p. 839-849.
-
Park H. S., Adeli H. A neural dynamics model for structural optimization – Application to plastic design of structures. Computers and Structures, Vol. 57, Issue 3, 1995, p. 391-399.
-
Adeli H., Kim H. Wavelet-hybrid feedback-least mean square algorithm for robust control of structures. Journal of Structural Engineering, Vol. 130, Issue 1, 2004, p. 128-137.
-
Kim H., Adeli H. Hybrid feedback-least mean square algorithm for structural control. Journal of Structural Engineering, Vol. 130, Issue 1, 2004, p. 120-127.
-
Adeli H., Jiang X. Intelligent Infrastructure: Neural Networks, Wavelets, and Chaos Theory for Intelligent Transportation Systems and Smart Structures. CRC Press, 2008.
-
Zongmin M., Zhang F., Yan L., Cheng J. Extracting knowledge from fuzzy relational databases with description logic. Integrated Computer Aided Engineering, Vol. 18, Issue 2, 2011, p. 181-200.
-
Rigatos G. G. Adaptive fuzzy control with output feedback for H∞ tracking of Siso nonlinear systems. International Journal of Neural Systems, Vol. 18, Issue 4, 2008, p. 305-320.
-
Siddique N., Adeli H. Computational Intelligence: Synergies of Fuzzy Logic, Neural Networks and Evolutionary Computing. Wiley, 2013.
-
Adeli H., Sarma K. C. Cost Optimization of Structures: Fuzzy Logic, Genetic Algorithms, and Parallel Computing. Wiley, 2006.
-
Korkmaz S. A review of active structural control: challenges for engineering informatics. Computers and Structures, Vol. 89, Issues 23-24, 2011, p. 2113-2132.
-
El-Khoury O., Adeli H. Recent advances on vibration control of structures under dynamic loading. Archives of Computational Methods in Engineering, Vol. 20, Issue 4, 2013, p. 353-360.
-
Soto M. G., Adeli H. Placement of control devices for passive, semi-active, and active vibration control of structures. Scientia Iranica, Vol. 20, Issue 6, 2013, p. 1567-1578.
-
Basu B., Bursi O. S., Casciati F., Casciati S., Del Grosso A. E., Domaneschi M., Faravelli L., Holnicki-Szulc J., Irschik H., Krommer M., Lepidi M., Martelli A., Ozturk B., Pozo F., Pujol G., Rakicevic Z., Rodellar J. A European association for the control of structures joint perspective. recent studies in civil structural control across Europe. Structural Control and Health Monitoring, Vol. 21, Issue 12, 2014, p. 1414-1436.
-
Gutierrez Soto M., Adeli H. Tuned mass dampers. Archives of Computational Methods in Engineering, Vol. 20, Issue 4, 2013, p. 419-431.
-
Adeli H., Saleh A. Control, Optimization, and Smart Structures: High-Performance Bridges and Buildings of the Future. Wiley, 1999.
-
Nigdeli S. M., Boduroğlu M. H. Active tendon control of torsionally irregular structures under near-fault ground motion excitation. Computer-Aided Civil and Infrastructure Engineering, Vol. 28, Issue 9, 2013, p. 718-736.
-
Amini F., Hazaveh N. K., Rad A. A. Wavelet PSO-based LQR algorithm for optimal structural control using active tuned mass dampers. Computer-Aided Civil and Infrastructure Engineering, Vol. 28, Issue 7, 2013, p. 542-557.
-
Boulkaibet I., Mthembu L., De Lima Neto F., Marwala T. Finite element model updating using fish school search and volitive particle swarm optimization. Integrated Computer-Aided Engineering, Vol. 22, Issue 4, 2015, p. 361-376.
-
Shabbir F., Omenzetter P. Particle swarm optimization with sequential niche technique for dynamic finite element model updating. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 5, 2015, p. 359-375.
-
Dai H., Zhang H., Wang W. A Multiwavelet neural network-based response surface method for structural reliability analysis. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 2, 2015, p. 151-162.
-
Alhasan A., White D. J., De Brabanter K. Wavelet filter design for pavement roughness analysis. Computer-Aided Civil and Infrastructure Engineering, Vol. 31, Issue 12, 2016, p. 907-920.
-
Soleymani M., Khodadadi M. Adaptive fuzzy controller for active tuned mass damper of a benchmark tall building subjected to seismic and wind loads. The Structural Design of Tall and Special Buildings, Vol. 23, Issue 10, 2014, p. 781-800.
-
Tinkir M., Kalyoncu M., Şahin Y. Deflection control of two-floors structure against northridge earthquake by using PI controlled active mass damping. Applied Mechanics and Materials, Vol. 307, 2013, p. 126-130.
-
Wang N., Adeli H. Robust vibration control of wind-excited highrise building structures. Journal of Civil Engineering and Management, Vol. 21, Issue 8, 2015, p. 967-976.
-
Ubertini F., Venanzi I., Comanducci G. Considerations on the implementation and modeling of an active mass driver with electric torsional servomotor. Mechanical Systems and Signal Processing, Vol. 58, 2015, p. 53-69.
-
Yang D.-H., Shin J.-H., Lee H., Kim S.-K., Kwak M. K. Active vibration control of structure by active mass damper and multi-modal negative acceleration feedback control algorithm. Journal of Sound and Vibration, Vol. 392, 2017, p. 18-30.
-
Teng J., Xing H. B., Lu W., Li Z. H., Chen C. J. Influence analysis of time delay to active mass damper control system using pole assignment method. Mechanical Systems and Signal Processing, Vol. 80, 2016, p. 99-116.
-
Fu T. S., Johnson E. A. Active control for a distributed mass damper system. Journal of Engineering Mechanics, Vol. 140, Issue 2, 2014, p. 426-429.
-
Amini F., Samani M. Z. A wavelet-based adaptive pole assignment method for structural control. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 6, 2014, p. 464-477.
-
Yanik A., Aldemir U., Bakioglu M. A new active control performance index for vibration control of three-dimensional structures. Engineering Structures, Vol. 62, Issue 63, 2014, p. 53-64.
-
Omidi E., Mahmoodi S. N., Shepard W. S. Multi positive feedback control method for active vibration suppression in flexible structures. Mechatronics, Vol. 33, 2016, p. 23-33.
-
Nazarimofrad E., Zahrai S. M. Seismic control of irregular multistory buildings using active tendons considering soil-structure interaction effect. Soil Dynamics and Earthquake Engineering, Vol. 89, 2016, p. 100-115.
-
Liu J., Chen X., Gao J., Zhang X. Multiple-source multiple-harmonic active vibration control of variable section cylindrical structures: a numerical study. Mechanical Systems and Signal Processing, Vol. 81, 2016, p. 461-474.
-
Yavuz Ş., Malgaca L., Karagülle H. Analysis of active vibration control of multi-degree-of-freedom flexible systems by Newmark method. Simulation Modelling Practice and Theory, Vol. 69, 2016, p. 136-148.
-
Bakule L., Rehák B., Papík M. Decentralized networked control of building structures. Computer-Aided Civil and Infrastructure Engineering, Vol. 31, Issue 11, 2016, p. 871-886.
-
An Y., Spencer B. F., Ou J. A test method for damage diagnosis of suspension bridge suspender cables. Computer‐Aided Civil and Infrastructure Engineering, Vol. 30, Issue 10, 2015, p. 771-784.
-
Kim H., Adeli H. Wavelet-hybrid feedback linear mean squared algorithm for robust control of cable-stayed bridges. Journal of Bridge Engineering, Vol. 10, Issue 2, 2005, p. 116-123.
-
Pereira E., Díaz I. M., Hudson E. J., Reynolds P. Optimal control-based methodology for active vibration control of pedestrian structures. Engineering Structures, Vol. 80, 2014, p. 153-162.
-
Wang N., Adeli H. Self-constructing wavelet neural network algorithm for nonlinear control of large structures. Engineering Applications of Artificial Intelligence, Vol. 41, 2015, p. 249-258.
-
Adeli H., Hung S.-L. Machine Learning: Neural Networks, Genetic Algorithms, and Fuzzy Systems. Wiley, 1995.
-
Mitchell R., Cha Y.-J., Kim Y., Mahajan A. A. Active control of highway bridges subject to a variety of earthquake loads. Earthquake Engineering and Engineering Vibration, Vol. 14, Issue 2, 2015, p. 253-263.
-
Paris P. C. D., Pedrino E. C., Nicoletti M. C. Automatic learning of image filters using Cartesian genetic programming. Integrated Computer-Aided Engineering, Vol. 22, Issue 2, 2015, p. 135-151.
-
Pillon P. E., Pedrino E. C., Roda V. O., Nicoletti M. C. A hardware oriented ad-hoc computer-based method for binary structuring element decomposition based on genetic algorithms. Integrated Computer-Aided Engineering, Vol. 23, Issue 4, 2016, p. 369-383.
-
Hsu W.-Y. Assembling a multi-feature EEG classifier for left-right motor imagery data using wavelet-based fuzzy approximate entropy for improved accuracy. International Journal of Neural Systems, Vol. 25, Issue 8, 2015, p. 1550037.
-
Ponz-Tienda J. L., Pellicer E., Benlloch-Marco J., Andrés-Romano C. The fuzzy project scheduling problem with minimal generalized precedence relations. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 11, 2015, p. 872-891.
-
Bekdaş G., Nigdeli S. M. Mass ratio factor for optimum tuned mass damper strategies. International Journal of Mechanical Sciences, Vol. 71, 2013, p. 68-84.
-
Siddique N., Adeli H. Harmony search algorithm and its variants. International Journal of Pattern Recognition and Artificial Intelligence, Vol. 29, Issue 8, 2015, p. 1539001.
-
Siddique N., Adeli H. Hybrid harmony search algorithms. International Journal on Artificial Intelligence Tools, Vol. 24, Issue 6, 2015, p. 1530001.
-
Lazar I. F., Neild S. A., Wagg D. J. Using an inerter-based device for structural vibration suppression. Earthquake Engineering and Structural Dynamics, Vol. 43, Issue 8, 2014, p. 1129-1147.
-
Marian L., Giaralis A. Optimal design of a novel tuned mass-damper-inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Engineering Mechanics, Vol. 38, 2014, p. 156-164.
-
Jin X., Chen M. Z. Q., Huang Z. Minimization of the beam response using inerter- based passive vibration control configurations. International Journal of Mechanical Sciences, Vol. 119, 2016, p. 80-87.
-
Tan P., Xu K., Wang B., Chang C., Liu H., Zhou F. Development and performance evaluation of an innovative low-cost seismic isolator. Science China Technological Sciences, Vol. 57, Issue 10, 2014, p. 2050-2061.
-
Papalou A., Strepelias E. Effectiveness of particle dampers in reducing monuments’ response under dynamic loads. Mechanics of Advanced Materials and Structures, Vol. 23, Issue 2, 2016, p. 128-135.
-
Dai K., Wang J., Mao R., Lu Z., Chen S.-E. Experimental investigation on dynamic characterization and seismic control performance of a TLPD system. The Structural Design of Tall and Special Buildings, 2016, https://doi.org/10.1002/tal.1350.
-
Ruiz R. O., Taflanidis A. A., Lopez-Garcia D. Characterization and design of tuned liquid dampers with floating roof considering arbitrary tank cross-sections. Journal of Sound and Vibration, Vol. 368, 2016, p. 36-54.
-
Lu Z., Chen X., Zhang D., Dai K. Experimental and analytical study on the performance of particle tuned mass dampers under seismic excitation. Earthquake Engineering and Structural Dynamics, Vol. 46, Issue 5, 2017, p. 697-714.
-
Min K.-W., Kim J., Lee H.-R. A design procedure of two-way liquid dampers for attenuation of wind-induced responses of tall buildings. Journal of Wind Engineering and Industrial Aerodynamics, Vol. 129, 2014, p. 22-30.
-
Hejazi F., Toloue I., Jaafar M. S., Noorzaei J. Otimization of earthquake energy dissipation system by genetic algorithm. Computer-Aided Civil and Infrastructure Engineering, 2013, https://doi.org/10.1111/mice.12047.
-
Lee H., Yi C., Lee D., Arditi D. An advanced stochastic time‐cost tradeoff analysis based on a CPM-guided genetic algorithm. Computer‐Aided Civil and Infrastructure Engineering, Vol. 30, Issue 10, 2015, p. 824-842.
-
Mencía R., Sierra M. R., Mencía C., Varela R. Genetic algorithms for the scheduling problem with arbitrary precedence relations and skilled operators. Integrated Computer-Aided Engineering, Vol. 23, Issue 3, 2016, p. 269-285.
-
Hejazi F., Shoaei M. D., Tousi A., Jaafar M. S. Analytical model for viscous wall dampers. Computer-Aided Civil and Infrastructure Engineering, Vol. 31, Issue 5, 2016, p. 381-399.
-
Qian H., Li H., Song G., Guo W. Recentering shape memory alloy passive damper for structural vibration control. Mathematical Problems in Engineering, 2013, https://doi.org/10.1155/2013/963530.
-
Briones B., De la Llera J. Analysis, design and testing of an hourglass-shaped ETP-copper energy dissipation device. Engineering Structures, Vol. 79, 2014, p. 309-321.
-
Walsh K. K., Sallar G., Steinberg E. P. Modeling and validation of a passive resettable stiffness damper. Journal of Engineering Mechanics, Vol. 143, Issue 2, 2017, p. 4016114.
-
Yamamoto M., Sone T. Damping systems that are effective over a wide range of displacement amplitudes using metallic yielding component and viscoelastic damper in series. Earthquake Engineering and Structural Dynamics, Vol. 43, Issue 14, 2014, p. 2097-2114.
-
Shi X., Zhu S. Magnetic negative stiffness dampers. Smart Materials and Structures, Vol. 24, Issue 7, 2015, p. 72002.
-
Yan W., Xu W., Wang J., Chen Y. Experimental research on the effects of a tuned particle damper on a viaduct system under seismic loads. Journal of Bridge Engineering, Vol. 19, Issue 3, 2014, p. 4013004.
-
Miguel L. F. F., Fadel Miguel L. F., Lopez R. H. A firefly algorithm for the design of force and placement of friction dampers for control of man-induced vibrations in footbridges. Optimization and Engineering, Vol. 16, Issue 3, 2015, p. 633-661.
-
Chou J., Pham A. Smart artificial firefly colony algorithm-based support vector regression for enhanced forecasting in civil engineering. Computer‐Aided Civil and Infrastructure Engineering, Vol. 30, Issue 9, 2015, p. 715-732.
-
Takeya K., Sasaki E., Kobayashi Y. Design and parametric study on energy harvesting from bridge vibration using tuned dual-mass damper systems. Journal of Sound and Vibration, Vol. 361, 2016, p. 50-65.
-
Miguel L. F. F., Lopez R. H., Torii A. J., Miguel L. F. F., Beck A. T. Robust design optimization of TMDs in vehicle-bridge coupled vibration problems. Engineering Structures, Vol. 126, 2016, p. 703-711.
-
Camara A., Cristantielli R., Astiz M. A., Málaga-Chuquitaype C. Design of hysteretic dampers with optimal ductility for the transverse seismic control of cable-stayed bridges. Earthquake Engineering and Structural Dynamics, 2017, https://doi.org/10.1002/eqe.2884.
-
Attary N., Symans M., Nagarajaiah S., Reinhorn A. M., Constantinou M. C., Sarlis A. A., Pasala D. T. R., Taylor D. P. Experimental shake table testing of an adaptive passive negative stiffness device within a highway bridge model. Earthquake Spectra, Vol. 31, Issue 4, 2015, p. 2163-2194.
-
Attary N., Symans M., Nagarajaiah S., Reinhorn A. M., Constantinou M. C., Sarlis A. A., Pasala D. T. R., Taylor D. Performance evaluation of negative stiffness devices for seismic response control of bridge structures via experimental shake table tests. Journal of Earthquake Engineering, Vol. 19, Issue 2, 2015, p. 249-276.
-
Zeinali M., Mazlan S. A., Abd Fatah A. Y., Zamzuri H. A phenomenological dynamic model of a magnetorheological damper using a neuro-fuzzy system. Smart Materials and Structures, Vol. 22, Issue 12, 2013, p. 125013.
-
Cha Y.-J., Agrawal A. K., Friedman A., Phillips B., Ahn R., Dong B., Dyke S. J., Spencer B. F., Ricles J., Christenson R. Performance validations of semiactive controllers on large-scale moment-resisting frame equipped with 200-kN MR damper using real-time hybrid simulations. Journal of Structural Engineering, Vol. 140, Issue 10, 2014, p. 4014066.
-
Khalid M., Yusof R., Joshani M., Selamat H., Joshani M. Nonlinear Identification of a Magneto-Rheological Damper Based on Dynamic Neural Networks. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 3, 2014, p. 221-233.
-
Panakkat A., Adeli H. Recurrent Neural Network for Approximate Earthquake Time and Location Prediction Using Multiple Seismicity Indicators. Computer-Aided Civil and Infrastructure Engineering, Vol. 24, Issue 4, 2009, p. 280-292.
-
Xu Q., Chen J., Liu X., Li J., Yuan C. An ABC-BP-ANN algorithm for semi-active control for Magnetorheological damper. KSCE Journal of Civil Engineering, 2016, https://doi.org/10.1007/s12205-016-0680-5.
-
Lin G.-L., Lin C.-C., Chen B.-C., Soong T.-T. Vibration control performance of tuned mass dampers with resettable variable stiffness. Engineering Structures, Vol. 83, 2015, p. 187-197.
-
Chu S.-Y., Yeh S.-W., Lu L.-Y., Peng C.-H. A leverage-type stiffness controllable mass damper for vibration mitigation of structures. Structural Control and Health Monitoring, Vol. 24, 4, p. 2017-1896.
-
Etedali S., Sohrabi M. R., Tavakoli S. Optimal PD/PID control of smart base isolated buildings equipped with piezoelectric friction dampers. Earthquake Engineering and Engineering Vibration, Vol. 12, Issue 1, 2013, p. 39-54.
-
Cao L., Downey A., Laflamme S., Taylor D., Ricles J. Variable friction device for structural control based on duo-servo vehicle brake: Modeling and experimental validation. Journal of Sound and Vibration, Vol. 348, 2015, p. 41-56.
-
Garrido H., Curadelli O., Ambrosini D. Experimental and theoretical study of semi-active friction tendons. Mechatronics, Vol. 39, 2016, p. 63-76.
-
Shi Y., Becker T. C., Furukawa S., Sato E., Nakashima M. LQR control with frequency-dependent scheduled gain for a semi-active floor isolation system. Earthquake Engineering & Structural Dynamics, Vol. 43, Issue 9, 2014, p. 1265-1284.
-
Qu C., Li H.-N., Huo L., Yi T.-H. Optimum value of negative stiffness and additional damping in civil structures. Journal of Structural Engineering, Vol. 143, Issue 8, 2017, p. 4017068.
-
Luu M., Martinez-Rodrigo M. D., Zabel V., Könke C. Semi-active magnetorheological dampers for reducing response of high-speed railway bridges. Control Engineering Practice, Vol. 32, 2014, p. 147-160.
-
Weber F. Semi-active vibration absorber based on real-time controlled MR damper. Mechanical Systems and Signal Processing, Vol. 46, Issue 2, 2014, p. 272-288.
-
Chen Z. H., Lam K. H., Ni Y. Q. Enhanced damping for bridge cables using a self-sensing MR damper. Smart Materials and Structures, Vol. 25, 8, p. 2016-85019.
-
Heo G., Kim C., Jeon S., Lee C., Seo S. A study on a MR damping system with lumped mass for a two-span bridge to diminish its earthquake-induced longitudinal vibration. Soil Dynamics and Earthquake Engineering, Vol. 92, 2017, p. 312-329.
-
Andersson A., O’Connor A., Karoumi R. Passive and adaptive damping systems for vibration mitigation and increased fatigue service life of a tied arch railway bridge. Computer-Aided Civil and Infrastructure Engineering, Vol. 30, Issue 9, 2015, p. 748-757.
-
Shen W., Zhu S. Harvesting energy via electromagnetic damper: Application to bridge stay cables. Journal of Intelligent Material Systems and Structures, Vol. 26, Issue 1, 2015, p. 3-19.
-
Gur S., Mishra S. K., Bhowmick S., Chakraborty S. Compliant liquid column damper modified by shape memory alloy device for seismic vibration control. Smart Materials and Structures, Vol. 23, Issue 10, 2014, p. 105009.
-
Hogsberg J., Brodersen M. L. Hybrid viscous damper with filtered integral force feedback control. Journal of Vibration and Control, Vol. 22, Issue 6, 2014, p. 1645-1656.
-
Jalaeefar A., Asgarian B. A simple hybrid damping device with energy-dissipating and re-centering characteristics for special structures. The Structural Design of Tall and Special Buildings, Vol. 23, Issue 7, 2014, p. 483-499.
-
Cu V. H., Han B. A stay cable with viscous damper and tuned mass damper. Australian Journal of Structural Engineering, Vol. 16, Issue 4, 2015, p. 316-323.
-
Cu V. H., Han B., Pham D. H. Tuned mass-high damping rubber damper on a taut cable. KSCE Journal of Civil Engineering, Vol. 21, Issue 3, 2017, p. 928-936.
-
Pham M.-N., Ahn H.-J. Horizontal active vibration isolator (HAVI) using electromagnetic planar actuator (EPA). International Journal of Precision Engineering and Manufacturing-Green Technology, Vol. 2, Issue 3, 2015, p. 269-274.
-
Liu C., Jing X., Li F. Vibration isolation using a hybrid lever-type isolation system with an X-shape supporting structure. International Journal of Mechanical Sciences, Vol. 98, 2015, p. 169-177.
-
Huang X., Liu X., Hua H. On the characteristics of an ultra-low frequency nonlinear isolator using sliding beam as negative stiffness. Journal of Mechanical Science and Technology, Vol. 28, Issue 3, 2014, p. 813-822.
-
Wu W., Chen X., Shan Y. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness. Journal of Sound and Vibration, Vol. 333, Issue 13, 2014, p. 2958-2970.
-
Calvi P. M., Moratti M., Calvi G. M. Seismic isolation devices based on sliding between surfaces with variable friction coefficient. Earthquake Spectra, Vol. 32, Issue 4, 2016, p. 2291-2315.
-
Chen H.-Y., Liang J.-W. Adaptive wavelet neural network controller for active suppression control of a diaphragm-type pneumatic vibration isolator. International Journal of Control, Automation and Systems, Vol. 15, Issue 3, 2017, p. 1456-1465.
About this article
The authors gratefully acknowledge the support given by Fundamental Research Grant Scheme, Ministry of Education, Malaysia (FRGS-Project No. FP004-2014B), Postgraduate Research Grant (PPP-Project No. PG177-2016A) and University of Malaya Research Grant (UMRG-Project No. RP004A-13AET).
