Comparison of hysteresis of high accuracy positioning system with piezoelectric actuators

Čereška, A.; Maskeliūnas, R.; Ragulskienė, J.; Lu, Guang Qing

doi:10.21595/jve.2017.18424

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2017

Check for updates

Comparison of hysteresis of high accuracy positioning system with piezoelectric actuators

A. Čereška¹

R. Maskeliūnas²

J. Ragulskienė³

Guang Qing Lu⁴

^{1, 2}Vilnius Gediminas Technical University, J. Basanavičiaus str. 28, LT-03224 Vilnius, Lithuania

³Kaunas University of Technology, Studentu str. 50-146, LT-51368 Kaunas, Lithuania

⁴Jinan University, West Huangpu str. 601, 510632 Guangzhou, China

Corresponding Author:

A. Čereška

Cite the article Download PDF

Downloads 1512

Abstract

In the paper, high accuracy positioning systems with flexible elements are investigated. In the analyzed systems, piezoelectric actuators are used for the transmission of motion and the hystereric phenomenon in them is investigated. Effect of the hysteretic phenomena to the precision of the high accuracy positioning systems is of special importance. For the investigations, a special experimental setup was designed and produced as well as the method of the experimental procedure was proposed. The experimental setup includes a computer, a piezocontroller, an inductive displacement sensor and a dynamic data collector. The dynamic data collector is used for the collection of data and for the transfer of data to the software for further processing. Numerical modelling of the hysteretic was performed by using the Matlab/Simulink software. In the process of investigations, it was determined that the maximum dispersion error of the hysteretic model is less than 5 % when compared with the experimental results. Thus, it is concluded that the proposed method of hysteretic phenomenon modelling is suitable for modelling of high accuracy positioning systems with flexible elements, which are controlled by piezoelectric actuators.

1. Introduction

In recent years the demand for positioning systems of very high precision is increasing. Those systems must be able to perform positioning with a precision of micrometers or nanometers. They are important in the process of very small semiconductor production as well as in the production of positioning and measurement machines of very high accuracy. For this purpose, piezoelectric actuators are used in positioning systems. Piezoelectric actuators are noted for their high speed of operation, high stiffness, high efficiency of conversion of energy. But the accuracy of positioning systems of this type is influenced by the hysteretic phenomenon taking place in the piezoelements.

Hysteretic effect in the piezoelectric actuator is characterised as a nonlinear relationship between the voltage supplied to the actuator and the displacement of the actuator. Because of this nonlinear phenomena displacement errors of the piezoelectric actuator reach 10-15 %. Therefore, in order to achieve maximum precision of the positioning platform it is necessary to eliminate the hysteretic effect [1, 2].

A much smaller hysteretic effect of the displacement is obtained by controlling the feeding signal of the piezoelement not by the value of the voltage, but by the value of the charge. This result is even further improved by using the system with feedback.

Scientists Lei L. and others [3] applied the subdivision of unit value by using the Preisach model for the determination of the hysteretic phenomenon and its compensation in piezoelectric actuators. The authors performed the subdivision of unit value on the basis of the algorithm of the method of least squares. The parameters of the hysteretic phenomenon were determined on the basis of the Preisach model.

In the research papers [4-7] the investigations of the positioning systems with two piezoelectric actuators which have two degrees of freedom are presented. The main problem of the research was to suppress the hysteretic nonlinearity in the piezoelectric actuator. For the solution of this problem a new algorithm was proposed. Dynamic qualities of the hysteretic effect were formulated by using the Bouc-Wen model. Optimal parameters of the hysteretic effect were identified by using the procedure based on the proposed new algorithm.

Scientists Vahid Hassani and Tegoeh Tjahjowidodo [8] in their investigation chose the positioning platform to be shaped as a pyramid and the analyzed mechanism to be controlled on the basis of piezoelectric principle. This mechanism has three degrees of freedom and it operates in two modes: stepwise and resonance. A model describing the dynamic motion of the mechanism was investigated at various different frequencies.

Scientists B. Gozen and O. Burak Ozdoganlar [9] proposed a method for feedforward control (control without feedback) of stack piezoactuators which has three degrees of freedom and operates at a single frequency. By using this method, the dynamic qualities of the stack piezoelectric actuator were presented as functions of reaction frequency harmonics, which were obtained by using the laser Doppler vibrometer.

In the papers [10, 11] the nonlinear modelling of hysteretic phenomenon of the mechanism with deformable elements was performed. In the investigated mechanism, piezoelectric actuators were used in order to ensure the necessary motion of the system.

Scientists Yingfeng S., Geng W., Lothar G. and others in their important research papers [12-14] solve the problems of hysteretic nonlinearity. They perform the control of hysteretic effects by using the two basic methods: feedforward (without feedback) and with feedback.

In the process of creation and design of the precise positioning system operating on the principle of stack piezoactuators and in order to obtain positioning results of highest precision it is necessary to compensate for the errors that take place because of the hysteretic phenomenon.

In this paper, the investigations of hysteretic phenomena of the precise positioning system with two axes which is controlled by the piezocontrollers are presented. The investigated system may be set on the rotating platform of the angle comparator for positioning of circular raster and code scales of anglular converters.

2. Structure and principle of operation of the positioning system

High accuracy positioning system with two axes which are shown in Fig. 1 is investigated. It consists from two packet piezoelectric actuators operating mutually perpendicularly and is located in the deformable mechanism of a continuous body. Piezoelectric actuator changes electrical energy into mechanical energy on the basis of the piezoeffect and this results in finite displacement or force. Packet piezoelectric actuator “PICMA P-887” produced by “Physik Instrumente” was used. Length of the actuator is 36 mm and at the maximum allowable voltage 120 V it becomes 38 μm longer.

Fig. 1General view of a dual axis micropositioning stage: 1 – piezostack actuators; 2 – compliant mechanism; 3 – coupling plates; 4 – coupling bolts

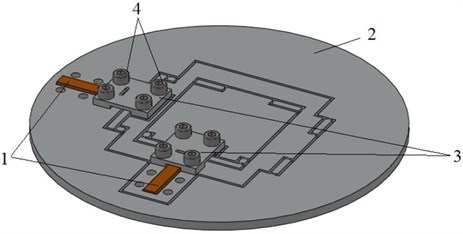
Packet piezoactuator 1 acts to the chain of deformable mechanisms 3, it pushes the platform 6 in the direction of the $y$ axis. Another packet piezoactuator 2 is mounted in the platform 6 moving in the direction of the $y$ axis and it acts to the chain of deformable mechanisms 4 and pushes the platform 5 in the direction of the $x$ axis. Chains of deformable elements 7 and 8 operate as elements reducing the stiffness. Displacements in the directions of the $x$ and $y$ axes are mutually independent.

The platform is a single body produced by the special method of processing by using electrical erosion from the aluminium mould material Al 7075 T-6. Method of processing by electrical erosion ensures the precision tolerance ±m.

3. Design of the experimental setup and procedure of experimental investigation

General view of the experimental setup is shown in Fig. 2. Experimental procedure was conducted when the system was operating in the direction of the $x$ axis.

Fig. 3Experimental setup

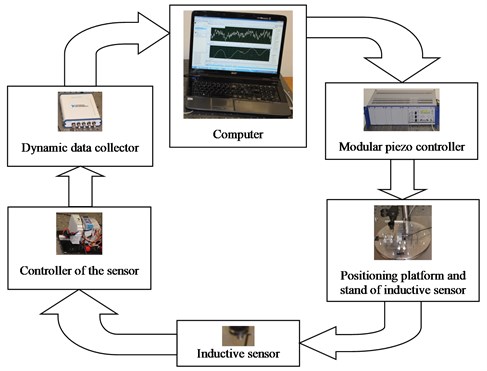
Measurements of the positioning system precision were performed in the following sequence:

1) Experimental setup was designed and produced.

2) The signal was generated by using the software “PI MicroMove” which is produced by “Physik Instrumente”, afterwards the signal was controlled by the module of piezo controller “LVPZT E-501” also produced by “Physik Instrumente” and then it was transferred to the piezoelectric executor “PICMA P-887”.

3) Voltage of the signal was increased from 0 V up to 12 V, when the voltage value reached 12 V, it was reduced back to 0 V.

4) Voltage of the signal was increased from 0 V up to 120 V, when the voltage value reached 120 V, it was reduced back to 0 V.

5) At the same time, the sensor of induction type “U3” was measuring the reaction of the system to the signal, that was measured by the mechanical displacement of the platform. The sensor was controlled by the controller “ECL 202” produced by “Lion Precision”.

6) Results of the performed measurements were registered by using the specialized software “Sound and Vibration Assistant” with the help of the module “LABview” by using the dynamic data collector “NI USB-4431” produced by “National Instruments”.

4. Model of hysteretic behaviour of the positioning platform

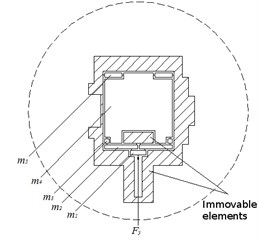
Various types of mechanisms of continuous body type with flexible elements are described by mathematical models. They are presented in [15, 16] and other related papers. In this case, the continuous body is considered as a mechanism consisting from stiff and elastic elements. Flexible element shown in Fig. 4 and used in the proposed mathematical model is considered as a spring having three degrees of freedom. Its rotational stiffness is $k_{ϕ}$ and displacement stiffnesses are $k_{x}$ and $k_{y}$ . The corresponding damping coefficients are $c_{ϕ}$ , $c_{x}$ and $c_{y}$ .

Values of parameters of the dynamic model are presented in the paper [17].

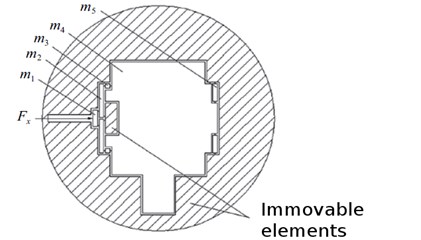
Dynamic model with the indicated applied force is shown in Fig. 5. Full dynamic model of the system is shown in detail in Fig. 6.

Fig. 4Model of flexible element

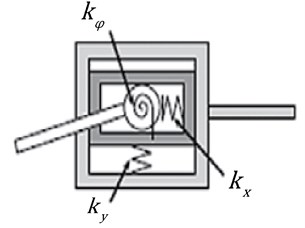
Fig. 5a) Dynamic model under applied force acting in the direction of the x axis, and b) dynamic model under applied force acting in the direction of the y axis: m1, m2, m3, m4, m5 – masses of rigid elements, Fx, Fy – forces acting to the mechanism

a) Dynamic model under applied force acting in the direction of the x axis, and b) dynamic model under applied force acting in the direction of the y axis: m1, m2, m3, m4, m5 – masses of rigid elements, Fx, Fy – forces acting to the mechanism

a)

b)

When the system performs a mechanical motion rigid bodies move by the coordinates $x_{1}$ , $x_{2}$ , $x_{3}$ , $x_{4}$ , $x_{5}$ and their centers of mass displace by the coordinates $x_{1 C}$ , $x_{2 C}$ , $x_{3 C}$ , $x_{4 C}$ and rotate by small angles $ϕ_{1}$ , $ϕ_{3}$ . The lengths of rigid bodies are $L_{1}$ , $L_{4}$ and the lengths of their balancing are $a_{1}$ , $b_{1}$ . The system was divided into seven rigid bodies, masses of which are $m_{11} = m_{12} = m_{1}$ , $m_{21} = m_{22} = m_{2}$ , $m_{3 X}$ , $m_{3 Y}$ , $m_{41} = m_{42} = m_{4}$ . Moments of inertia are $I_{1 C}$ , $I_{4 C}$ .

For the proposed dynamic model of the system the Lagrange equation is applied:

1

\frac{d}{d t} (\frac{\partial T}{\partial {\dot{q}}_{i}}) - \frac{\partial T}{\partial q_{i}} + \frac{\partial Φ}{\partial {\dot{q}}_{i}} + \frac{\partial Π}{\partial q_{i}} = F_{i},

where $T$ , $Π$ are the kinetic and potential energies of the system, $Φ$ is the dissipative function, $q_{i}$ is the $i$ th generalised coordinate, ${\dot{q}}_{i}$ is the time derivative of the $i$ th generalised coordinate, $F_{i}$ is the generalised force acting according to the $i$ th generalised coordinate.

Kinetic energy of the system has the following form:

2

T = m_{1} {\dot{x}}_{1}^{2} + m_{1} {\dot{x}}_{1} {\dot{ϕ}}_{1} L_{1} + m_{2} {\dot{x}}_{2 C}^{2} + \frac{m_{3} {\dot{x}}_{3 C}^{2}}{2} + m_{4} {\dot{x}}_{5}^{2} + m_{4} {\dot{x}}_{5} {\dot{ϕ}}_{3} L_{4}

+ \frac{m_{1} {\dot{ϕ}}_{1}^{2} L_{1}^{2}}{4} + I_{1 C} {\dot{ϕ}}_{1}^{2} + \frac{m_{4} {\dot{ϕ}}_{3}^{2} L_{4}^{2}}{4} + I_{4 C} {\dot{ϕ}}_{3}^{2} .

Fig. 6Dynamic model of the precise positioning system: the system in the status of equilibrium is shown in red colour, while the deflected system is shown in black colour [17]

Dynamic model of the precise positioning system: the system in the status of equilibrium is shown in red colour, while the deflected system is shown in black colour [17]

Potential energy of the system has the following form:

3

P = x_{1}^{2} k_{x} + x_{5}^{2} k_{y} + 3 ϕ_{1}^{2} k_{ϕ} + 2 ϕ_{3}^{2} k_{ϕ} + k_{x} (x_{2 C} - x_{3 C})^{2} + k_{x} (x_{1} - x_{2 C} + L_{1} ϕ_{1})^{2}

+ k_{y} (x_{5} - x_{3 C} + L_{4} ϕ_{3})^{2} + k_{x} (x_{1} - η_{1} + b_{1} ϕ_{1})^{2} .

Dissipative function of the system has the following form:

4

F = c_{x} ({\dot{x}}_{1} - {\dot{x}}_{2 C} + {\dot{ϕ}}_{1} L_{1})^{2} + c_{y} ({\dot{x}}_{5} - {\dot{x}}_{3 C} + {\dot{ϕ}}_{3} L_{4})^{2} + 3 {\dot{ϕ}}_{1} c_{ϕ}

+ 2 ϕ_{3}^{2} c_{ϕ} + {\dot{x}}_{1}^{2} c_{x} + {\dot{x}}_{5}^{2} c_{y} + c_{x} ({\dot{x}}_{2 C} - {\dot{x}}_{3 C})^{2} + c_{x} ({\dot{x}}_{1} - {\dot{η}}_{1} b_{1})^{2} .

By using the Lagrange Eq. (1) calculations of the motion of the platform in the generalised coordinates $x_{i}$ , $ϕ_{i}$ were performed. Matlab/Simulink software was used in the investigation.

Then the model of the hysteretic phenomena of the high accuracy positioning system was proposed, which is shown in Fig. 7 [17].

Fig. 7Dynamic simulation model of the entire system

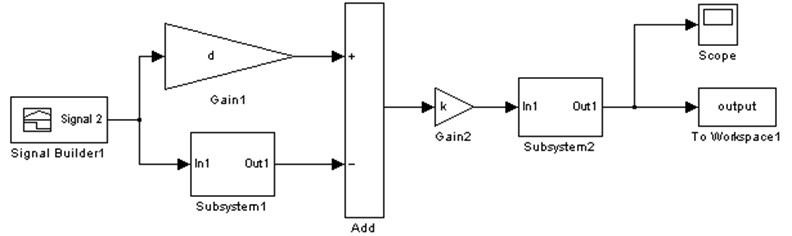
For the model of hysteretic phenomena of the piezo element the Bouc-Wen model was used. This model uses only three variables for the definition of hysteretic behaviour. The model is described by the first order of nonlinear differential function [17]:

5

\dot{h} (t) = α \dot{u} - β |\dot{u} (t)| \cdot h (t) \cdot {|h (t)|}^{n - 1} - γ \dot{u} {|h (t)|}^{n},

where $h (t)$ defines the variable hysteretic status, $u (t)$ is the supplied voltage, parameters $α$ , $β$ , $γ$ control the amplitudes and the shape of the hysteresis loop, $n$ is the coefficient describing the fluency of elastic and plastic reactions (the value of $n = 1$ is chosen) [2, 18]. The parameters $α$ , $β$ , $γ$ are determined experimentally in the process of modelling.

In order to obtain the mathematical model of the positioning platform the Matlab/Simulink software was used. The program was created by including the previously presented expressions of kinetic and potential energies as well as the expression of the dissipative function. The program performed differentiation with respect to the generalised coordinates $x_{i}$ and $ϕ_{i}$ by taking into account their derivatives ${\dot{x}}_{i}$ , ${\dot{ϕ}}_{i}$ and the time $t$ . After performing the calculations the matrix was produced, on the basis of which the dynamic model of the platform of the positioning system was obtained.

5. Results of investigation of hysteretic behaviour of the positioning platform

After performing the experimental investigation of hysteretic behaviour of high accuracy positioning system the results were obtained and are shown in Fig. 8 and Fig. 9. In the presented graphical relationships the dependence of the system displacement to the voltage supplied to the piezoelectric actuator is shown.

When the voltage increases from 0 V up to 12 V and decreases from 12 V up to 0 V in steps of 1 V it was obtained that the largest errors between the curves of the voltage increase and decrease are at 80 V: in the direction of the $x$ axis they are 0.344 μm and in the direction of the $y$ axis they are 0.264 μm. The biggest difference from the results obtained by the experimental investigations is 0.084 μm in the direction of the $x$ axis and 0.014 μm in the direction of the $y$ axis (see Fig. 8).

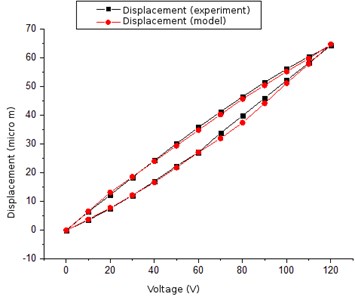
When the voltage increases from 0 V up to 120 V and decreases from 120 V up to 0 V in steps of 10 V it was obtained that the largest errors between the curves of the voltage increase and decrease are at 80 V: in the direction of the $x$ axis they are 7.91 μm and in the direction of the $y$ axis they are 7.55 μm. The biggest difference from the results obtained by the experimental investigations is 0.08 μm in the direction of the $x$ axis and 0.13 μm in the direction of the $y$ axis (see Fig. 9).

From the obtained results, the effect of the hysteretic phenomenon is seen. Because of the influence of this effect the dispersion of the results for the displacement of the experimental setup reaches 8.67 m. This constitutes 13.54 % of the maximum allowable displacement of the system.

By comparing the experimental results with the numerical ones, it is seen that the maximum non-coincidence of displacements is 2.42 m. It constitutes 3.78 % of maximum elongation.

Fig. 8Comparison of hysteresis loops, when the voltage is 12 V: experimental and theoretical

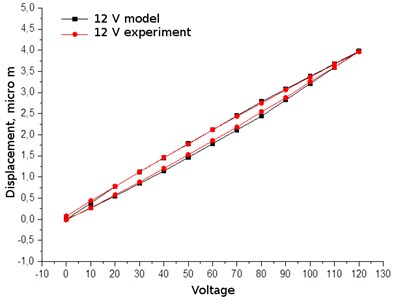
Fig. 9Comparison of hysteresis loops, when the voltage is 120 V: experimental and theoretical

6. Conclusions

Error of results of theoretical and experimental investigations of hysteretic phenomena is smaller than 5 % when maximum displacement of the system is 2.42 m. Thus, it can be concluded that the proposed method of modelling of hysteretic behaviour is suitable for precise positioning systems with flexible elements.

After performing the analysis of the results of experimental investigations it was determined that the dispersion of the positioning system is 13.54 % when the displacement of the system reaches its maximum value. This is a large error for the precise positioning system, therefore, compensation of the hysteretic effect must be performed. For this purpose, special control algorithms are developed.

Thus, it is concluded that the proposed method of modelling of the hysteretic phenomenon is suitable for modelling of precise positioning systems with flexible elements, which are controlled by piezoelectric actuators.

References

Chih-Jer L., Po-Ting L. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. Computers and Mathematics with Applications, Vol. 64, 2012, p. 766-787.

Publisher
Yangmin L., Qingsong X. Adaptive sliding mode control with perturbation estimation and PID sliding surface for motion tracking of a piezo-driven micromanipulator. IEEE Transactions on Control Systems Technology, Vol. 18, 2010, p. 798-810.

Publisher
Lei L., Kok Kiong T., Si-Lu C. SVD-based Preisach hysteresis identification and composite control of piezo actuators. ISA Transactions, Vol. 57, 2012, p. 430-438.

Publisher
Yanding Q., Bijan S., Yanling T. Design issues in a decoupled XY stage: static and dynamics modeling, hysteresis compensation, and tracking control. Sensors and Actuators A: Physical, Vol. 194, 2013, p. 95-105.

Publisher
Chih-Jer L., Shu-Yin C. Evolutionary algorithm based feedforward control for contouring of a biaxial piezo-actuated stage. Mechatronics, Vol. 19, 2009, p. 829-839.

Publisher
Chih-Jer L., Po-Ting L. Particle swarm optimization based feedforward controller for a XY PZT positioning stage. Mechatronics, Vol. 22, 2012, p. 614-628.

Search CrossRef
Vahid H., Tegoeh T. Structural response investigation of a triangular-based piezoelectric drive mechanism to hysteresis effect of the piezoelectric actuator. Mechanical Systems and Signal ProcessingVol. 36, 2013, p. 210-223.

Publisher
Vahid H., Tegoeh T. Dynamic modeling of 3-DOF pyramidal-shaped piezo-driven mechanism. Mechanizm and Machine Theory, Vol. 70, 2013, p. 225-245.

Publisher
Arda G. B., Burak Ozdoganlar O. A method for open-loop control of dynamic motions of piezo-stack actuators. Sensors and Actuators A: Physical, Vol. 184, 2012, p. 160-172.

Publisher
Do T. N., Tjahjowidodo T., Lau M. W. S. Hysteresis modeling and position control of tendon-sheath mechanism in flexible endoscopic systems. Mechatronics, Vol. 24, 2014, p. 12-22.

Publisher
Chih-Jer, L.; Po-Ting, L. Particle swarm optimization based feedforward controller for a XY PZT positioning stage. Mechatronics, Vol. 22, 2012, p. 614-628.

Publisher
Yingfeng S., Kam K. L. Accounting for hysteresis in repetitive control design: nanopositioning example. Automatica, Vol. 48, 2012, p. 1751-1758.

Publisher
Geng W., Chunlin G., Xiaojun Z. Precision control of piezo-actuated optical deflector with nonlinearity correction based on hysteresis model. Optics and Laser Technology, Vol. 57, 2014, p. 26-31.

Publisher
Lothar G., Jens B. Model-based piezoelectric hysteresis and creep compensation for highly-dynamic feedforward rest-to-rest motion control of piezoelectrically actuated flexible structures. International Journal of Engineering Science, Vol. 47, 2009, p. 1193-1207.

Publisher
Li Y., Xu Q. Modeling and performance evaluation of a flexure-based XY parallel micromanipulator. Mechanism and Machine Theory, Vol. 44, 2009, p. 2127-2152.

Publisher
Dong J., Yao Q., Ferreira P. M. A novel parallel-kinematics mechanisms for integrated, multi-axis nanopositioning. Part 2: Dynamics, control and performance analysis. Precision Engineering, Vol. 32, 2008, p. 20-33.

Publisher
Čereška A., Augustinavičius G. Pozicionavimo sistemos su lanksčiaisiais elementais histerezės efekto tyrimas. Mokslas-Lietuvos ateitis, Vol. 6, 2014, p. 607-611.

Publisher
Yung-Tien L., Kuo-Ming C., Wen-Zen L. Model reference adaptive control for a piezo-positioning system. Precision Engineering, Vol. 34, 2010, p. 62-69.

Publisher

About this article

Received

03 April 2017

Accepted

26 June 2017

Published

15 August 2017

SUBJECTS

Vibration generation and control

DOI

https://doi.org/10.21595/jve.2017.18424

Keywords

hysteretic phenomenon

piezoelectric actuator

high accuracy

positioning system

Acknowledgements

The authors acknowledge gratefully the National Natural Science Foundation of China for supporting the researches of Project No. 51475211, including the study of this paper.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 05 18

Enhancing model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators using modified differential evolution algorithm

Hafiz Muhammad Umar, Ruichen Yu, Zhiyuan Gao, Hesheng Zhang

Research article

2020 05 07

Stress analysis of plate with opposite semicircular notches and adhesively bonded piezoelectric actuators

Ahmed Abuzaid, Meftah Hrairi, Hashim Kabrein

Research article

2019 03 15

Open-loop linearization for piezoelectric actuator with inverse hysteresis model

Markus Riepold, Semir Maslo, Ge Han, Christian Henke, Ansgar Trächtler

Research article

2017 05 15

Hysteresis linearization control of a novel hybrid vibration isolator

Yang Zhang, Zhaobo Chen, Yinghou Jiao, Xiaoyu Wang

A. Čereška, R. Maskeliūnas, J. Ragulskienė, and G. Q. Lu, “Comparison of hysteresis of high accuracy positioning system with piezoelectric actuators,” Journal of Vibroengineering, Vol. 19, No. 5, pp. 3556–3563, Aug. 2017, https://doi.org/10.21595/jve.2017.18424

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.18424
UR  - https://doi.org/10.21595/jve.2017.18424
TI  - Comparison of hysteresis of high accuracy positioning system with piezoelectric actuators
T2  - Journal of Vibroengineering
AU  - Čereška, A.
AU  - Maskeliūnas, R.
AU  - Ragulskienė, J.
AU  - Lu, Guang Qing
PY  - 2017
DA  - 2017/08/15
PB  - JVE International Ltd.
SP  - 3556-3563
IS  - 5
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{_ere_ka_2017,
	doi = {10.21595/jve.2017.18424},
	url = {https://doi.org/10.21595/jve.2017.18424},
	year = 2017,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {5},
	pages = {3556--3563},
	author = {A. {\v{C}}ere{\v{s}}ka and R. Maskeli{\={u}}nas and J. Ragulskien{\.{e}} and Guang Qing Lu},
	title = {Comparison of hysteresis of high accuracy positioning system with piezoelectric actuators},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]A. Čereška, R. Maskeliūnas, J. Ragulskienė, and G. Q. Lu, “Comparison of hysteresis of high accuracy positioning system with piezoelectric actuators,” Journal of Vibroengineering, vol. 19, no. 5, pp. 3556–3563, Aug. 2017, doi: 10.21595/jve.2017.18424.

Copy IEEE

Copied to clipboard!

Čereška, A., R. Maskeliūnas, J. Ragulskienė, and Guang Qing Lu. “Comparison of Hysteresis of High Accuracy Positioning System with Piezoelectric Actuators.” Journal of Vibroengineering 19, no. 5 (August 15, 2017): 3556–63. https://doi.org/10.21595/jve.2017.18424.

Copy Chicago

Copied to clipboard!

Comparison of hysteresis of high accuracy positioning system with piezoelectric actuators

Abstract

1. Introduction

2. Structure and principle of operation of the positioning system

3. Design of the experimental setup and procedure of experimental investigation

4. Model of hysteretic behaviour of the positioning platform

5. Results of investigation of hysteretic behaviour of the positioning platform

6. Conclusions

References

About this article

Related Articles