Enhancing model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators using modified differential evolution algorithm

Umar, Hafiz Muhammad; Yu, Ruichen; Gao, Zhiyuan; Zhang, Hesheng

doi:10.21595/vp.2023.23309

Vibroengineering Procedia

Browse Procedia

Published: 18 May 2023

Check for updates

Enhancing model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators using modified differential evolution algorithm

Hafiz Muhammad Umar¹

Ruichen Yu²

Zhiyuan Gao³

Hesheng Zhang⁴

^{1, 2, 3, 4}School of Mechatronic Engineering and Automation, Shanghai University, Shanghai, 200444, China

Corresponding Author:

Zhiyuan Gao

Cite the article Download PDF

Downloads 200

Abstract

This paper presents a study on improving the estimation accuracy and convergence rate of hysteresis modeling of MFC actuators using mutation enhanced differential evolution (MEDE) algorithm, a modified version of the differential evolution algorithm. The proposed MEDE algorithm uses three mutation strategies, i.e., best, rand, and pbest. To model the secondary path of a smart flexible beam with MFC actuators, a Hammerstein model that combines an asymmetric Bouc-Wen model with an ARX model connected in series is proposed. The fitness function values of the Hammerstein model are compared with evolutionary algorithms.

Enhancing model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators using modified differential evolution algorithm

Highlights

A Hammerstein model that combines an asymmetric Bouc-Wen model and an autoregressive-exogenous (ARX) model is proposed for accurately modeling the hysteresis behavior of MFC actuators.
The MEDE algorithm based on multiple mutation strategies is used to optimize the fitness of the proposed Hammerstein model for accurately modeling the hysteresis behavior of MFC actuators. The algorithm provides better convergence rate and model estimation accuracy.
The MFC actuators are used to control the active vibration of a smart cantilever beam, demonstrating the practical application of the proposed approach in the field of smart structures and vibration control.

1. Introduction

MFC is a popular piezocomposite transducer with high-performance characteristics, widely used in various applications [1]. However, the performance of MFC actuator is limited by its nonlinear and hysteretic behavior [2].

Bouc-Wen model is popular for describing hysteresis nonlinearity of piezoelectric materials [3-5], but it can only account for symmetric hysteresis. Since MFC actuators exhibit asymmetric hysteresis, alternative model needs to be developed. Wang Geng [6] suggested a modified Bouc-Wen (MBW) model to capture the asymmetric hysteresis nonlinearity of the piezoelectric actuator. Since the actual hysteretic nonlinear curve of MFC actuator is related to rate. To tackle the aforementioned challenge, one approach is to connect the hysteretic nonlinear model in series with a linear model, resulting in a Hammerstein model [7]. For example, Konstantinos Krikelis proposed a Hammerstein model that integrates the Prandtl-Ishlinskii hysteresis model with a linear recursive neural network [8].

The aim is to enhance the model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators without explicitly identifying the model parameters. Instead of identifying the model parameters, we use the fitness function output, including fitnessbestX, favg, fmax, fmin, and fstd, to compare the performance of different optimization algorithms. In this study, the MEDE algorithm based on multiple mutation strategies is used to optimize the fitness of the proposed Hammerstein model. Section 2 provides a detailed description of the proposed Hammerstein model. Section 3 presents the methodology for applying the MEDE algorithm. The results are presented in Section 4. Section 5 finally describes the conclusion.

2. Model for hysteresis characterization in MFC actuators

2.1. Bouc-Wen hysteresis model

A classical Bouc-Wen model defined by the following equations, can characterize the dynamic behavior of MFC actuators [9, 10]:

1

Z (t) = M \ddot{x} (t) + D \dot{x} (t) + K x (t) = K [L u (t) - h (t)],

2

\dot{h} (t) = α L \dot{u} (t) - β |\dot{u} (t)| h (t) - γ \dot{u} (t) |h (t)|,

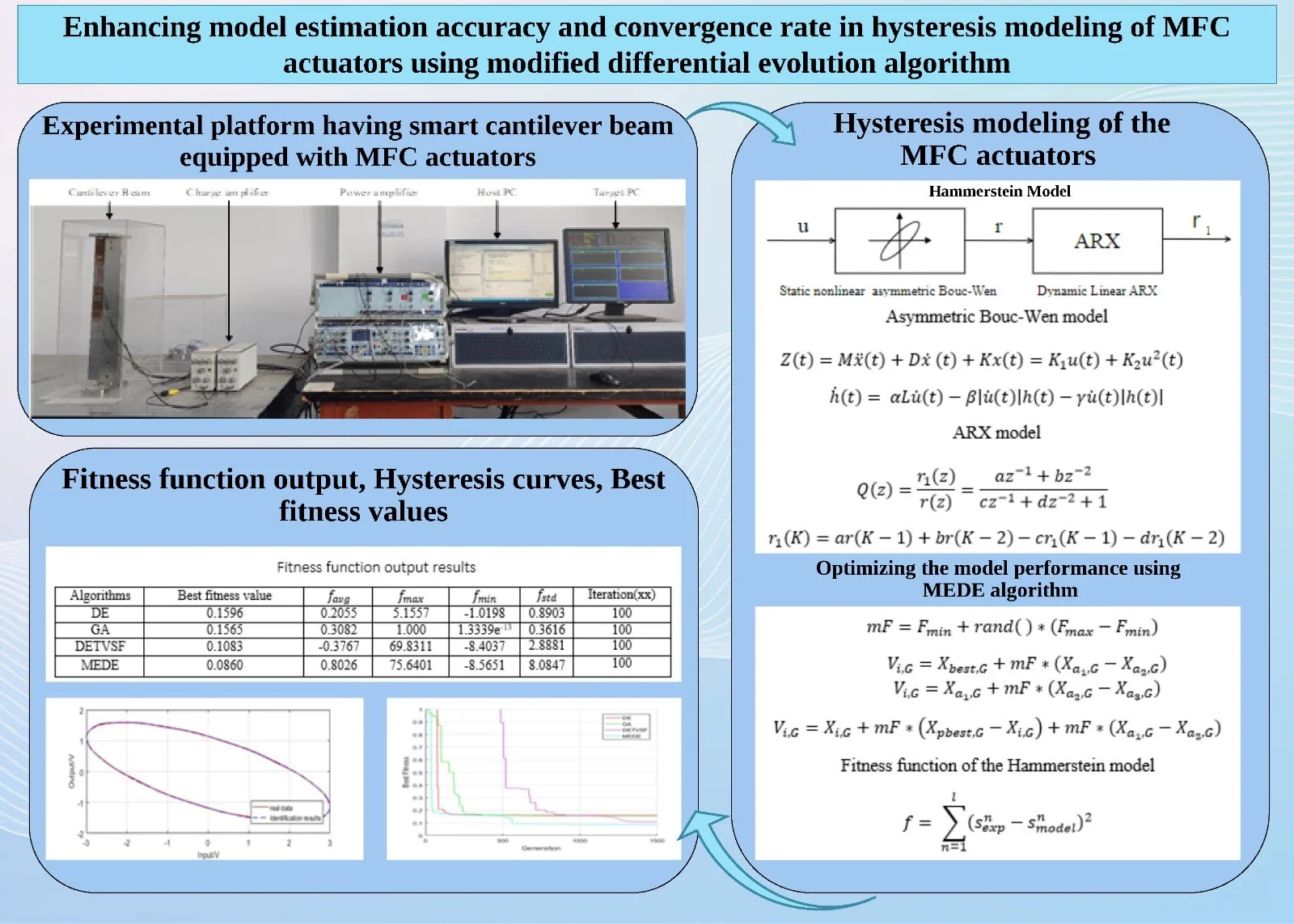
where, the linear Eq. (1) relating the input voltage ( $u)$ to the output displacement ( $h)$ and nonlinear differential Eq. (2) describing the displacement change over time. $α$ $β$ and $γ$ are hysteresis loop parameters; $M$ , $D$ , $K$ and $L$ are the mass, damping coefficient, stiffness and piezoelectric coefficient respectively. It can describe symmetric hysteresis due to its assumption that the nonlinearity is symmetric about the origin. This mathematical formulation results in symmetric hysteresis loops for both loading and unloading cycles as shown in Fig. 1. The Bouc-Wen model is specifically designed to account for the hysteresis phenomenon, which is a characteristic property of MFC actuators.

Fig. 1Symmetry of Buc-Wen model

$Z (t)$ is made up of two components: a hysteretic component $K h (t)$ with memory and non-hysteretic component $p (t) = K L u (t)$ without memory. As a result $Z (t) = p (u (t)) - K h (t)$ .

2.2. Asymmetric Bouc-Wen model in discrete form

The MFC actuator exhibits asymmetric hysteresis, so the model needs to improve. This paper proposes a modification in Eq. (1) of the classical Bouc-Wen model with the non-hysteretic component $p (t)$ to the polynomial $p (u (t))$ :

3

p (u (t) = d_{1} u (t) + d_{2} u^{2} (t),

where, $d_{1}$ and $d_{2}$ are the parameters. Thus, the asymmetric Bouc-Wen model can be given by:

4

Z (t) = M \ddot{x} (t) + D \dot{x} (t) + K x (t) = K_{1} u (t) + K_{2} u^{2} (t),

5

\dot{h} (t) = α L \dot{u} (t) - β |\dot{u} (t)| h (t) - γ \dot{u} (t) |h (t)| .

Before being employed in digital control systems, the asymmetric Bouc-Wen model must be discretized. As a result, we use the Laplace transform and bilinear transform, as shown below:

6

r (K) = - \frac{1}{e_{1}} [f_{1} r (K - 1) + g_{1} r (K - 2) - e h_{1} (K) - f h_{1} (K - 1) - g h_{1} (K - 2)],

7

h_{1} (K) = d_{1} u (K) + d_{2} u^{2} (K) - h (K),

8

h (K) = α L u (K) - β |u (K)| h (K - 1) - γ u (K) |h (K - 1)| + h (K - 1) .

From the Eq. (6); $e = T_{s}^{2}$ , $f = 2 T_{s}^{2}$ , $g = T_{s}^{2}$ , $e_{1} = 4 M + 2 D T_{s} + K T_{s}^{2}$ , $f_{1} = 2 K T_{s}^{2} - 8 M$ , $g_{1} = 4 M - 2 D T_{s} + K T_{s}^{2}$ . The variable $T_{s}$ denotes the sample time.

2.3. Development of a Hammerstein model for improved modeling of MFC actuators

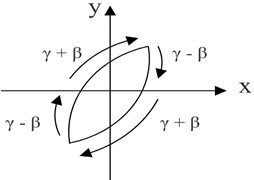
To improve the model of MFC actuators further, a novel approach using a Hammerstein model that combines a discrete asymmetric Bouc-Wen model with a linear component with dynamic behavior is proposed. The model accounts for the rate-dependent hysteresis nonlinearity of MFC actuators. The proposed model comprises two modules: a static nonlinear component represented by the asymmetric Bouc-Wen model, and a dynamic linear component represented by the ARX model. The input signal first passes through the static nonlinearity block, which captures the actuator’s asymmetric behavior. The output of this block is then fed into the linear dynamic system block, which is modeled using a second-order ARX model as shown in Fig. 2. The ARX model is as follows:

9

Q (z) = \frac{r_{1} (z)}{r (z)} = \frac{a z^{- 1} + b z^{- 2}}{c z^{- 1} + d z^{- 2} + 1},

10

r_{1} (K) = a r (K - 1) + b r (K - 2) - c r_{1} (K - 1) - d r_{1} (K - 2),

where, $a$ , $b$ , $c$ and $d$ are the parameters of an ARX model.

Fig. 2Proposed Hammerstein model structure

3. Methodology

3.1. The traditional differential evaluation (DE) algorithm

DE algorithm is a widely used optimization method belonging to evolutionary algorithms family. It involves maintaining a population of candidate solutions and improving them iteratively by combining their features [11]. It is divided into the following parts:

3.1.1. Initialization

To initialize the DE algorithm, a population of target vectors of size $N P$ is generated. Each target vector is a row vector of dimension $D$ , denoted as $X_{i, G} = \{x_{1, G}, x_{2, G}, x_{3, G}, \dots, x_{N P, G}\}$ . $X_{m i n}$ and $X_{m a x}$ represent the lower and upper bounds of the solution space for each dimension. A common method is to generate initial population using a uniform distribution where each element is generated as $X_{i, j} = X_{m i n} + r a n d (0,1) * (X_{m a x} - X_{m i n})$ , where $j$ ranges from $1$ to $D$ ; $r a n d (0,1)$ is a random number between 0 and 1.

3.1.2. Mutation

The DE algorithm mutates the current population to generate new candidate solutions. The mutation operator perturbs a target vector $X_{i, G}$ to create a mutant vector $V_{i, G}$ using a customizable parameter called, mutation factor denoted as $m F$ . The mutation techniques are presented as [12].

DE / rand/ 1:

11

V_{i, G} = X_{a_{1}, G} + m F * (X_{a_{2}, G} - X_{a_{3}, G}) .

DE / best / 1:

12

V_{i, G} = X_{b e s t, G} + m F * (X_{a_{1}, G} - X_{a_{2}, G}) .

DE / current-to-best / 1:

13

V_{i, G} = X_{i, G} + m F * (X_{b e s t, G} - X_{i, G}) + m F * (X_{a_{1}, G} - X_{a_{2}, G}),

where, $X_{a_{1}, G}$ , $X_{a_{2}, G}$ , and $X_{a_{3} G}$ are three randomly selected base vectors, $a_{1}$ , $a_{2}$ , and $a_{3}$ are indices of different vectors in the population, and $a_{1} \neq a_{2} \neq a_{3} \neq i$ . $X_{b e s t, G}$ is the best vector in the population. Mutation factor $m F$ is a positive value normally varies between 0 and 2.

3.1.3. Crossover

Crossover, combine the mutant vector with the target vector. The crossover operation randomly selects a dimension of the mutant vector and replaces it with the corresponding dimension of the target vector to form a trial vector. The binomial crossover as follows:

14

H_{i, G}^{j} = \{\begin{matrix} V_{i, G}^{j}, {r a n d}_{j} \leq C R o r j = j_{r a n d}, \\ X_{i, G}^{j}, o t h e r w i s e, \end{matrix}

where, $C R$ is a positive value between 0 and 1, ${r a n d}_{j}$ ∈ [0, 1] is a uniform random number, and $j_{r a n d}$ is a randomly selected index within the range of dimensions of the vectors.

3.1.4. Selection

In selection, each candidate vector competes with its corresponding target vector based on their fitness value. The most common selection method in DE algorithm is the greedy selection, as follows:

15

X_{i, G + 1} = \{\begin{matrix} H_{i, G}, f (H_{i, G}) \leq f (X_{i, G}), \\ X_{i, G}, o t h e r w i s e, \end{matrix}

where, $f (H_{i, G})$ and $f (X_{i, G})$ are the objective functions to be minimized.

3.2. The mutation enhanced differential evolution (MEDE) algorithm

The MEDE algorithm is a modified version of the DE algorithm, which incorporates multiple mutation strategies and a dynamic mutation factor range. The multiple mutation strategies allow the algorithm to explore different regions of the search space simultaneously, while the dynamic mutation factor range helps to balance the global and local search abilities of the algorithm. Each individual in the population is mutated using one of the three mutation strategies: ‘best’, ‘rand’, or ‘current-to-pbest’ selected randomly. ‘best’ uses the best solution identified so far as the base vector, ‘rand’ uses a randomly selected solution as the base vector, and ‘current-to-pbest’ uses a set of pbest solutions and a randomly selected solution as the base vector. The modified mutation factor and mutation strategies describe as follows:

16

m F = F_{m i n} + r a n d () * (F_{m a x} - F_{m i n}) .

DE / best / 1:

17

V_{i, G} = X_{b e s t, G} + m F * (X_{a_{1}, G} - X_{a_{2}, G}) .

DE / rand / 1:

18

V_{i, G} = X_{a_{1}, G} + m F * (X_{a_{2}, G} - X_{a_{3}, G}) .

DE / current-to-pbest / 1:

19

V_{i, G} = X_{i, G} + m F * (X_{p b e s t, G} - X_{i, G}) + m F * {(X}_{a_{1}, G} - X_{a_{2}, G}),

where, $F_{m i n}$ and $F_{m a x}$ are the lower bond and upper bond mutation factors respectively. $X_{p b e s t, G}$ is picked at random as one of the top 100p% of the present population with $p$ ∈ (0, 1]. The MEDE algorithm can be used to optimize in case of fitness of Hammerstein. The fitness function for a proposed model, can be expressed mathematically as:

20

f = \sum_{n = 1}^{l} (s_{e x p}^{n} - {s_{m o d e l}^{n})}^{2},

where $s_{e x p}$ is the measured output, $s_{m o d e l}$ is the predicted output. The smaller the fitness function value, the closer the match between the predicted output and the actual experimental data.

4. Experimental setup and results

4.1. Experiment setup

The experimental platform utilized in this study is an active vibration control (AVC) experimental platform built in the Advanced Perception and Control laboratory, Shanghai University. It consists of a robust cantilever beam system equipped with MFC actuators and sensors, along with a power amplifier, charge amplifier, target PC, and host PC. The MFC actuators used were M5628-P2, while the sensors used were M0714-P2. Fig. 3 presents a photo of the experimental setup, which was captured by our team in February 2023.

Fig. 3Experimental setup for the cantilever beam system

4.2. Results

Table 1 displays the results.

Table 1Fitness function results

Algorithms	Best fitness value	$f_{a v g}$	$f_{m a x}$	$f_{m i n}$	$f_{s t d}$	Iteration (xx)
DE	0.1596	0.2055	5.1557	–1.0198	0.8903	100
GA	0.1565	0.3082	1.000	1.3339e^-13	0.3616	100
DETVSF	0.1083	–0.3767	69.8311	–8.4037	2.8881	100
MEDE	0.0860	0.8026	75.6401	–8.5651	8.0847	100

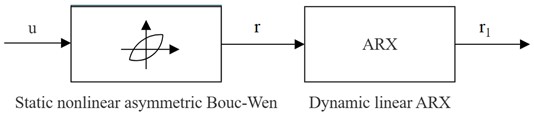
Fig. 4(a) compares the hysteresis curves of real data (actual experiment) with identification findings (Hammerstein model). Fig. 4(b) compares the greatest fitness value for various algorithms. MEDE’s best fitness value is more consistent with the experimental response than DE, GA, and DETVSF. As a result, the proposed MEDE algorithm produces significantly superior results.

Fig. 4Comparison of real data and identification results hysteresis curves and best fitness values

a) Hysteresis curve comparison

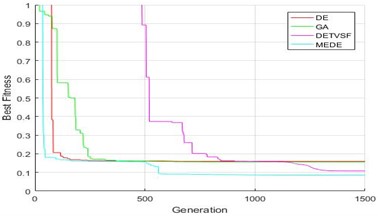
b) Best fitness value comparison

5. Conclusions

This paper proposes an improved hysteresis model that combines an asymmetric Bouc-Wen model with an ARX model connected in series to form a Hammerstein model and an optimization algorithm called MEDE. The proposed model accurately describes the Hammerstein hysteresis loop, while the MEDE algorithm optimizes the model’s performance. The comparison of MEDE with other algorithms shows that it provides more satisfactory optimal performance in terms of the fitness function.

References

J. Zhou, J. Zhou, W. Chen, J. Tian, J. Shen, and P. Zhang, “Macro fiber composite-based active and efficient suppression of low-frequency vibration of thin-walled composite beam,” Composite Structures, Vol. 299, p. 116019, Nov. 2022, https://doi.org/10.1016/j.compstruct.2022.116019

Publisher
M. S. Rana, H. R. Pota, and I. R. Petersen, “Nonlinearity effects reduction of an AFM piezoelectric tube scanner using MIMO MPC,” IEEE/ASME Transactions on Mechatronics, Vol. 20, No. 3, pp. 1458–1469, 2015.

Publisher
M. Salah and A. Saleem, “Hysteresis compensation-based robust output feedback control for long-stroke piezoelectric actuators at high frequency,” Sensors and Actuators A: Physical, Vol. 319, p. 112542, Mar. 2021, https://doi.org/10.1016/j.sna.2021.112542

Publisher
X. Xue, X. Wu, L. Chen, and Q. Sun, “Bouc-Wen modeling to hysteresis nonlinear in macro fiber composite (MFC) actuator,” International Journal of Applied Electromagnetics and Mechanics, Vol. 45, No. 1-4, pp. 965–971, May 2014, https://doi.org/10.3233/jae-141931

Publisher
Y.-L. Yang, Y.-D. Wei, J.-Q. Lou, L. Fu, G. Tian, and M. Wu, “Hysteresis modeling and precision trajectory control for a new MFC micromanipulator,” Sensors and Actuators A: Physical, Vol. 247, pp. 37–52, Aug. 2016, https://doi.org/10.1016/j.sna.2016.05.027

Publisher
G. Wang, G. Chen, and F. Bai, “Modeling and identification of asymmetric Bouc-Wen hysteresis for piezoelectric actuator via a novel differential evolution algorithm,” Sensors and Actuators A: Physical, Vol. 235, pp. 105–118, Nov. 2015, https://doi.org/10.1016/j.sna.2015.09.043

Publisher
L. Yang, Z. Zhao, Y. Zhang, and D. Li, “Rate-dependent modeling of piezoelectric actuators for nano manipulation based on fractional hammerstein model,” Micromachines, Vol. 13, No. 1, p. 42, Dec. 2021, https://doi.org/10.3390/mi13010042

Publisher
K. Krikelis, K. van Berkel, and M. Schoukens, “Artificial neural network hysteresis operators for the identification of hammerstein hysteretic systems,” IFAC-PapersOnLine, Vol. 54, No. 7, pp. 702–707, 2021, https://doi.org/10.1016/j.ifacol.2021.08.443

Publisher
Royson D. D. ’Souza, Bineesh Benny, Anil Sequeira, and Navin Karanth P., “Hysteresis modeling of amplified piezoelectric stack actuator for the control of the microgripper,” American Scientific Research Journal for Engineering, Technology, and Sciences, Vol. 15, No. 1, pp. 265–281, Jan. 2016.

Search CrossRef
M. Nafea M., Z. Mohamed, A. M. Abdullahi, M. R. Ahmad, and A. R. Husain, “Dynamic hysteresis based modeling of piezoelectric actuators,” Jurnal Teknologi, Vol. 67, No. 5, Mar. 2014, https://doi.org/10.11113/jt.v67.2834

Publisher
S. Das, S. S. Mullick, and P. N. Suganthan, “Recent advances in differential evolution – An updated survey,” Swarm and Evolutionary Computation, Vol. 27, pp. 1–30, Apr. 2016, https://doi.org/10.1016/j.swevo.2016.01.004

Publisher
G. Sun, B. Yang, Z. Yang, and G. Xu, “An adaptive differential evolution with combined strategy for global numerical optimization,” Soft Computing, Vol. 24, No. 9, pp. 6277–6296, May 2020, https://doi.org/10.1007/s00500-019-03934-3

Publisher

About this article

Received

06 April 2023

Accepted

29 April 2023

Published

18 May 2023

SUBJECTS

Dynamics of Smart and functionally graded materials

DOI

https://doi.org/10.21595/vp.2023.23309

Keywords

ARX model

asymmetric Bouc-Wen model

Hammerstein model

MFC actuators

mutation enhanced differential evolution algorithm

Acknowledgements

This work is supported by National Natural Science Foundation of China (Grant Nos. 52175101, 61503232).

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2020 11 09

A comparative study of phenomenological hysteretic models with application to recycled rubber-fibre reinforced bearings

Nagavinothini Ravichandran

Research article

2020 05 07

Hysteresis behaviour of different magnetorheological elastomer models: modelling and simulation

Thaer M. I. Syam, Asan G. A. Muthalif

Research article

2019 03 15

Open-loop linearization for piezoelectric actuator with inverse hysteresis model

Markus Riepold, Semir Maslo, Ge Han, Christian Henke, Ansgar Trächtler

Research article

2017 08 15

Modeling of a magneto-rheological (MR) damper using genetic programming

Pravin Singru, Ayush Raizada, Vishnuvardhan Krishnakumar, Akhil Garg, K. Tai, Varun Raj

H. M. Umar, R. Yu, Z. Gao, and H. Zhang, “Enhancing model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators using modified differential evolution algorithm,” Vibroengineering PROCEDIA, Vol. 49, pp. 246–252, May 2023, https://doi.org/10.21595/vp.2023.23309

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2023.23309
UR  - https://doi.org/10.21595/vp.2023.23309
TI  - Enhancing model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators using modified differential evolution algorithm
T2  - Vibroengineering PROCEDIA
AU  - Umar, Hafiz Muhammad
AU  - Yu, Ruichen
AU  - Gao, Zhiyuan
AU  - Zhang, Hesheng
PY  - 2023
DA  - 2023/05/18
PB  - JVE International Ltd.
SP  - 246-252
VL  - 49
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Umar_2023,
	doi = {10.21595/vp.2023.23309},
	url = {https://doi.org/10.21595/vp.2023.23309},
	year = 2023,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {49},
	pages = {246--252},
	author = {Hafiz Muhammad Umar and Ruichen Yu and Zhiyuan Gao and Hesheng Zhang},
	title = {Enhancing model estimation accuracy and convergence rate in hysteresis modeling of {MFC} actuators using modified differential evolution algorithm},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]H. M. Umar, R. Yu, Z. Gao, and H. Zhang, “Enhancing model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators using modified differential evolution algorithm,” Vibroengineering PROCEDIA, vol. 49, pp. 246–252, May 2023, doi: 10.21595/vp.2023.23309.

Copy IEEE

Copied to clipboard!

Umar, Hafiz Muhammad, Ruichen Yu, Zhiyuan Gao, and Hesheng Zhang. “Enhancing Model Estimation Accuracy and Convergence Rate in Hysteresis Modeling of MFC Actuators Using Modified Differential Evolution Algorithm.” Vibroengineering PROCEDIA 49 (May 18, 2023): 246–52. https://doi.org/10.21595/vp.2023.23309.

Copy Chicago

Copied to clipboard!

Enhancing model estimation accuracy and convergence rate in hysteresis modeling of MFC actuators using modified differential evolution algorithm

Abstract

Highlights

1. Introduction

2. Model for hysteresis characterization in MFC actuators

2.1. Bouc-Wen hysteresis model

2.2. Asymmetric Bouc-Wen model in discrete form

2.3. Development of a Hammerstein model for improved modeling of MFC actuators

3. Methodology

3.1. The traditional differential evaluation (DE) algorithm

3.1.1. Initialization

3.1.2. Mutation

3.1.3. Crossover

3.1.4. Selection

3.2. The mutation enhanced differential evolution (MEDE) algorithm

4. Experimental setup and results

4.1. Experiment setup

4.2. Results

5. Conclusions

References

About this article

Related Articles