Optimum suspension design for non-linear half vehicle model using particle swarm optimization (PSO) algorithm

Yildiz, Ahmet

doi:10.21595/vp.2019.21012

Vibroengineering Procedia

Browse Procedia

Published: 30 September 2019

Check for updates

Optimum suspension design for non-linear half vehicle model using particle swarm optimization (PSO) algorithm

Ahmet Yildiz¹

¹Bursa Uludag University, Engineering Faculty, Automotive Engineering Department, Bursa, Turkey

Cite the article Download PDF

Downloads 1630

CrossRef Citations 11

Abstract

This paper is considered with a non-linear suspension design for half vehicle model by using particle swarm optimization technique. To analyze the ride comfort, a five-degree of freedom system is built, and it is integrated with the Particle Swarm Optimization (PSO) for optimizing the vehicle vibrations. A multi-objective function is proposed as the sum of the minimum seat and vehicle body acceleration, the minimum suspension deflection and the constraints and the design variables of the optimization problem are selected as the spring and damping coefficients of the front and rear suspension and the non-linear spring and the linear damping coefficients of the seat. The simulations are carried out and the results are compared with the non-optimized values. It is demonstrated that the vehicle vibration is decreased significantly with the help of the optimum values of the suspension parameters.

1. Introduction

The vehicle vibration is one of the most important issues for the vehicle design process and many researches has been performed on this important topic in order to obtain high ride comfort. The vibration is mainly caused by road profile it should be compensated by using a well-designed suspension system. The suspension systems are generally divided into three main categories: Passive suspension, semi-active suspension and active suspension system [1-3]. Among them, the most common one is the passive suspension system because of its simplicity, efficiency and low cost [4]. In this type of suspension system, the spring and damper have the predefined characteristic, while in the semi-active and active suspension system, the reaction forces are controlled. On the other hand, by adding a non-linear spring into passive suspension, one can provide a more proper vibration response for different road profiles.

The vehicle vibration is analyzed by using three main mathematical models: Quarter vehicle model (QVM) [5, 6], half vehicle model (HVM) [7] and full vehicle model (FVM) [8]. The simplest of these is the QVM. This model supposes that the vehicle moves only in the vertical direction while HVM has four degrees of freedom (DOF) and it is used to determine the characteristic of the pitch motion as well. If the roll behavior of the vehicle needs to be analyzed, the most complex model, FVM, should be used, which has seven DOF. Furthermore, the seat and human model can be added to these models as well [9].

The optimization of vehicle vibration is very important to achieve better ride comfort and many tools are available for solving such complex engineering problems. The optimization problem can be solved by using a deterministic or a stochastic method that solves the objective function with systematical random inputs. One of the most common stochastic optimization methods is the Particle Swarm Optimization (PSO) technique and it has been applied for many different engineering problems as well as vehicle vibration.

In this paper, a half vehicle model is considered with non-linear seat suspension and five equations of motion are derived and then they are integrated with Particle Swarm Optimization (PSO) algorithm. The design variables of the optimization problem are the spring and damping coefficients of the front and rear suspension, and the non-linear spring and the linear damping coefficients of the seat. The objective function of the optimization problem is defined as the sum of the minimum seat and vehicle body acceleration and the minimum suspension deflection. The simulations are performed, and the results are compared with the non-optimized simulations. It has been found that much lower vibration amplitudes can be achieved by using optimum suspension parameters.

2. Mathematical model of 5 DOF vehicle

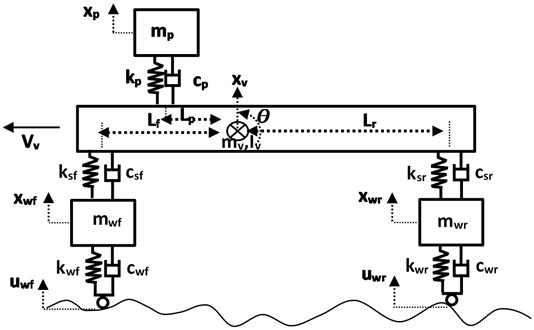
In this chapter, the mathematical model of the vehicle is derived to characterize the vehicle vibration with non-linear seat suspension. As shown in Fig. 1, the half vehicle model with non-linear seat spring system has five DOF: The vertical motion of the front ( $x_{w f}$ ) and rear wheel ( $x_{w r}$ ), the vertical ( $x_{p}$ ) and pitch motion of the vehicle body ( $θ$ ) and the vertical motion of the seat ( $x_{p}$ ).

Fig. 1A schematic diagram of a half vehicle model

In the mathematical model, the seat spring force $F_{s p}$ is considered as a cubic non-linear term:

1

F_{s p} = k_{p} x_{p} + k_{p n} x_{p}^{3},

where the $k_{p}$ and $k_{p n}$ are the spring coefficients of the seat suspension. Considering Newton-Euler approach, the equation of motions of HVM are derived as below:

2

m_{p} {\ddot{x}}_{p} - k_{p} (x_{v} - x_{p} - L_{p} θ) - k_{p n} (x_{v} - x_{p} - L_{p} θ)^{3} - c_{p} ({\dot{x}}_{v} - {\dot{x}}_{p} - L_{p} \dot{θ}) = 0,

3

m_{w f} {\ddot{x}}_{w f} - k_{w f} (u_{f} - x_{w f}) - c_{w f} ({\dot{u}}_{f} - {\dot{x}}_{w f}) + k_{s f} (x_{w f} - x_{v} + L_{f} θ)

+ c_{s f} ({\dot{x}}_{w f} - {\dot{x}}_{v} + L_{f} \dot{θ}) = 0,

4

m_{w r} {\ddot{x}}_{w r} - k_{w r} (u_{r} - x_{w r}) - c_{w r} ({\dot{u}}_{r} - {\dot{x}}_{w r}) + k_{s r} (x_{w r} - x_{v} - L_{r} θ)

+ c_{s r} ({\dot{x}}_{w r} - {\dot{x}}_{v} - L_{r} \dot{θ}) = 0,

5

m_{v} {\ddot{x}}_{v} + k_{p} (x_{v} - x_{p} - L_{p} θ) + k_{p n} (x_{v} - x_{p} - L_{p} θ)^{3} + c_{p} ({\dot{x}}_{v} - {\dot{x}}_{p} - L_{p} \dot{θ})

- k_{s f} (x_{w f} - x_{v} + L_{f} θ) - c_{s f} ({\dot{x}}_{w f} - {\dot{x}}_{v} + L_{f} \dot{θ})

- k_{s r} (x_{w r} - x_{v} - L_{r} θ) - c_{s r} ({\dot{x}}_{w r} - {\dot{x}}_{v} - L_{r} \dot{θ}) = 0,

6

I_{v} \ddot{θ} + k_{s f} (x_{w f} - x_{v} + L_{f} θ) L_{f} + c_{s f} ({\dot{x}}_{w f} - {\dot{x}}_{v} + L_{f} \dot{θ}) L_{f} - k_{p} (x_{v} - x_{p} - L_{p} θ) L_{p}

- k_{p n} (x_{v} - x_{p} - L_{p} θ)^{3} L_{p} - c_{p} ({\dot{x}}_{v} - {\dot{x}}_{p} - L_{p} \dot{θ}) L_{p}

- k_{s r} (x_{w r} - x_{v} - L_{r} θ) L_{r} - c_{s r} ({\dot{x}}_{w r} - {\dot{x}}_{v} - L_{r} \dot{θ}) L_{r} = 0,

where the $m_{w f}$ , $m_{w r}$ and $m_{v}$ denote the mass of front wheel, rear wheel and vehicle body while $k_{w f}$ , $k_{w r}$ and $c_{w f}$ , $c_{w r}$ are the stiffness and damper coefficients of the front and rear wheels respectively. The parameters $k_{s f}$ , $k_{s r}$ and $c_{s f}$ , $c_{s r}$ represent the stiffness and damper coefficients of the front and rear suspension system, which are the design variables. Also, the $θ$ and $I_{v}$ indicate the pith angle and the mass moment of the inertia of the vehicle body while $L_{r}$ , $L_{f}$ and $L_{p}$ are the distance from the rear suspension, front suspension and passenger axes to the center of gravity respectively. The subscript $w_{f}$ and $w_{r}$ denote the front and rear wheel.

The input road profile is represented with $u$ and it can be defined as a sinus function and it is given in Fig. 2 by using following equations:

7

u_{w f} = \{\begin{array}{l} h s i n (ω t), 0 \leq t \leq (\frac{λ}{V_{v}}), \\ 0, e l s e, \end{array}

8

u_{w r} = \{\begin{array}{l} h s i n (ω (t - ξ)), ξ \leq t \leq ξ + (\frac{λ}{V_{v}}), \\ 0, e l s e, \end{array}

where $ω$ and $V_{v}$ represent the angular frequency and the vehicle velocity which are equal to $ω = (2 π V_{v}) / λ$ and $ξ = (L_{f} + L_{r}) / V_{v}$ . The amplitude of the road profile is $h =$ 0.05 m, and the period of it $λ =$ 11.1 m.

Table 1Half vehicle parameters with the range of design variables

Parameter	Value/range	Parameter	Value/range
$m_{w f}$ [kg]	60	$c_{w f}$ [Ns/m]	10
$m_{w r}$ [kg]	50	$c_{w r}$ [Ns/m]	10
$m_{v}$ [kg]	700	$c_{s f}$ [Ns/m]	100-1500
$m_{p}$ [kg]	95	$c_{s r}$ [Ns/m]	100-1500
$k_{w f}$ [kN/m]	190	$c_{p}$ [Ns/m]	100-1500
$k_{w r}$ [kN/m]	190	$I_{v}$ [kgm²]	1400
$k_{s f}$ [kN/m]	15-55	$L_{f}$ [m]	1.2
$k_{s r}$ [kN/m]	15-55	$L_{r}$ [m]	1.7
$k_{p}$ [kN/m]	25-105	$L_{p}$ [m]	0.4
$k_{p n}$ [kN/m]	2500-10500	$V_{v}$ [m/s]	22.2

3. PSO optimization algorithms and its procedures

Particle Swarm Optimization (PSO) method is proposed by [10] firstly, which is a stochastic population-based optimization algorithm. The PSO algorithm is inspired by the group behavior of birds or fishes and it has a huge usage in the engineering applications [11]. A random group of particles is used to search the extreme point of the objective function and they follow the nearest ones in order to the find the best value of the target by means of the reproduced velocities until the finalize criteria is satisfied. About the PSO pseudo-codes more details are given as follows:

Step-1. Set parameters of PSO and generate the position of particles randomly according to the constrains and give the initial velocities to zero.

Step-2. Calculate the objective function and find the particle best position and global best of swarm.

Step-3. Update each particle position and velocity with the help of the equations (a) and (b). Restrict the velocity and position of particle in determined ranges to avoid exceeding the limits:

9

v_{i, j}^{k + 1} = w_{p} v_{i, j}^{k} + c_{1} r_{1} ((X_{P B})_{i, j}^{k} - X_{i, j}^{k}) + c_{2} r_{2} ((X_{G B})_{j}^{k} - X_{i, j}^{k}),

10

X_{i, j}^{k + 1} = X_{i, j}^{k} + v_{i, j}^{k + 1},

11

w_{p} = w_{m a x} - \frac{(w_{m a x} - w_{m i n}) k}{k_{m a x}},

where $i =$ 1, 2,…, $M$ , and $M$ is the swarm size, $j =$ 1, 2,…, $N$ , and $N$ is the variable size, $k =$ 1, 2,…, $k_{m a x}$ , the maximum number of iterations $k_{m a x} =$ 50 is, $v_{i, j}$ is the particle velocity, $X$ is the position of the particle, $X_{P B}$ and $X_{G B}$ are the best position of particles and global best of swarm, and the coefficients $w_{m a x} =$ 0.9 and $w_{m i n} =$ 0.4. $r_{1}$ and $r_{2}$ are random numbers between (0, 1) while the coefficient of cognitive and social acceleration factors are $c_{1} =$ 1.3 and $c_{2} =$ 2.8 respectively.

Step-4. Update the particle best position and global best of swarm by evaluating the fitness of each particle.

Step-5. Finalize the iterations if the requested conditions are achieved. If is it not satisfied, return the step 3.

In order to achieve better ride comfort of the vehicle, there are three main characteristic requirements from the system: Low amplitude of the seat acceleration to improve the ride comfort and low tire deflection for better road-holding ability and low suspension working space. Thus, the objective function is determined as the sum of the maximum acceleration of the seat and the sum of the squares of the constraints. There are three constrain functions regarding the real working conditions of the vehicle suspension system. These are the maximum acceleration of the seat and the vehicle body. Therefore, the objective function ( $F_{o b j}$ ) of the optimization problem and the three constrains ( $g_{1}$ , $g_{2}$ and $g_{3}$ ) are given as below:

12

F_{o b j} = 0.5 m a x |{\ddot{x}}_{p} (t)| + 0.5 m a x |{\ddot{x}}_{v} (t)|,

g_{1} = {\ddot{x}}_{p} (t) - 4.5 m / s^{2} \leq 0,

g_{2} = |x_{w f} (t) - u_{w f} (t)| - 0.06 m \leq 0,

g_{3} = |x_{w r} (t) - u_{w r} (t)| - 0.06 m \leq 0 .

According to the penalty function approach, the square of the constrains are added to the objective function. Design parameters of the optimization problem are selected as follow and the upper and lower limits of them are presented in Table 1:

13

x_{d} = \{k_{s f}, k_{s r}, k_{p}, k_{p n}, c_{s f}, c_{s r}, c_{p}\} .

Since the minimum amplitude of vehicle vibration is requested for better ride comfort, the cost function given in Eq. (12) is minimized by using the PSO algorithm. This minimization is carried out by solving the five equations of motions given Eqs. (2-6) using fourth order Runge-Kutta methods. The input of the differential equations is the road excitations given in Eqs. (7, 8). The values of the parameters of the simulations are given in Table 1.

4. Optimization results

The optimization results of the design variables obtained from the simulations are given in Table 2. Furthermore, the performances of the PSO are compared with un-optimized simulations as illustrated in the Fig. 2. The un-optimized simulation is performed with the following initial values of the suspension: $k_{s f} = k_{s r} =$ 35 kN/m, $c_{s f} = c_{s r} = c_{p} =$ 750 Ns/m, $k_{p} =$ 55 kN/m, $k_{p n} =$ 5500 kN/m.

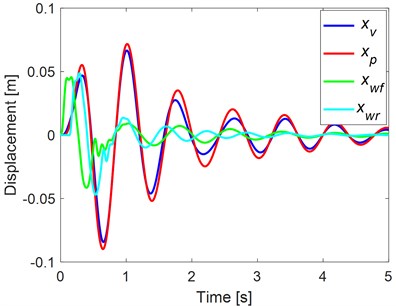
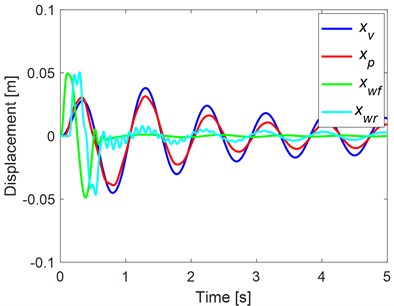
It is possible to see from the figure that the maximum amplitude of the seat and vehicle body acceleration are decreased significantly by using the optimization algorithm. The maximum seat acceleration of un-optimized simulation is 6.3965, while the maximum of optimized seat acceleration is equal to 3.1751. Thus, the maximum amplitude of the seat acceleration was reduced by about 50 percent. Similarly, the vehicle body acceleration is decreased by about 73 %. In Fig. 3, the displacements of the suspension system are illustrated to visualize the optimization effect. The results show that the optimum parameters can provide small amplitudes of displacements for the seat and the vehicle body. The constrains are also in the requested range, which are equal to $g_{1} =$ –0.9729 m/s², $g_{2} =$ –0.0083 m and $g_{3} =$ –0.0076 m.

Table 2The optimum design variables

Design variables	Optimization results
$k_{s f}$ [Nm]	15000
$k_{s r}$ [Nm]	15000
$k_{p}$ [Nm]	105000
$k_{p n}$ [Nm]	2500000
$c_{s f}$ [Ns/m]	1216.62
$c_{s r}$ [Ns/m]	99.99
$c_{p}$ [Ns/m]	170.34

Fig. 2Optimized and un-optimized simulation results: a) seat and b) vehicle body accelerations

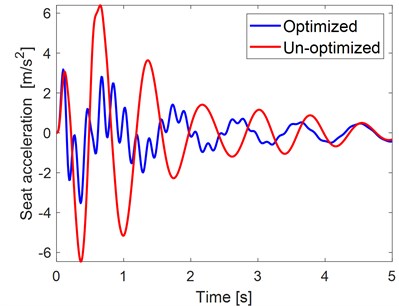
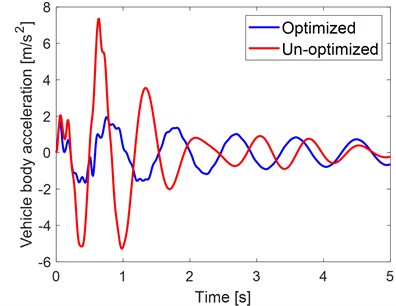
Fig. 3Simulation results: a) un-optimized and b) optimized displacements by using PSO algorithm

5. Conclusions

In this paper, five degrees of freedom of half vehicle with non-linear seat suspension model is handled to analyze and minimize the vehicle vibration for better ride comfort. A multi-objective function approach is used by using PSO algorithm. The design variables of the optimization problems are the stiffness and damping coefficients of the front and rear suspension, the non-linear and linear stiffness of the seat suspension and the damping coefficients of the seat. The fitness function is proposed as the sum of the minimum seat and vehicle body acceleration with constraints of optimization problems. The results of this paper show that the vibration amplitude can be decreased significantly thanks to the optimum design variables of the vehicle suspension by using PSO optimization technique. In future work, it is planning to validate these results by experiments and also to couple with different controller for the active suspension system.

References

Gillespie T. D. Fundamentals of Vehicle Dynamics. SAE International, Warrendale, 1996.

Search CrossRef
Jazar R. N. Vehicle Dynamics: Theory and Application. Springer International, New York, 2017.

Search CrossRef
Cao D., Song X., Ahmadian M. Editors’ perspectives: road vehicle suspension design, dynamics, and control. Vehicle System Dynamics, Vol. 49, Issues 1-2, 2011, p. 3-28.

Publisher
Alkhatiba R., Nakhaie Jazarb G., Golnaraghi M. F. Optimal design of passive linear suspension using genetic algorithm. Journal of Sound and Vibration, Vol. 275, Issues 3-5, 2004, p. 665-691.

Publisher
Kuznetsov A., Mammadov M., Sultan I., Hajilarov E. Optimization of a quarter-car suspension model coupled with the driver biomechanical effects. Journal of Sound and Vibration, Vol. 330, Issue 12, 2011, p. 2937-2946.

Publisher
Gundogdu O. Optimal seat and suspension design for a quarter car with driver model using genetic algorithms, International Journal of Industrial Ergonomics, Vol. 37, Issue 4, 2007, p. 327-332.

Publisher
Nariman Zadeh Salehpour N.-M., Jamali A., Haghgoo E. Pareto optimization of a five-degree of freedom vehicle vibration model using a multi-objective uniform-diversity genetic algorithm (MUGA). Engineering Applications of Artificial Intelligence, Vol. 23, Issue 4, 2010, p. 543-551.

Publisher
Guclu R. Fuzzy logic control of seat vibrations of a nonlinear full vehicle model. Nonlinear Dynamics, Vol. 40, 2005, p. 21-34.

Publisher
Ning D., Sun S., Li H., Du H., Li W. Active control of an innovative seat suspension system with acceleration measurement based friction estimation. Journal of Sound and Vibration, Vol. 384, Issue 11, 2016, p. 28-44.

Publisher
Eberhart R. C., Kennedy J. A new optimizer using particle swarm theory. Proceedings of the 6th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 1995.

Search CrossRef
Yildiz A. R. A novel particle swarm optimization approach for product design and manufacturing. The International Journal of Advanced Manufacturing Technology, Vol. 40, Issues 5-6, 2009, p. 617-628.

Publisher

Cited by

Optimization of dual-function suspension structures using particle swarm optimization approaches

Guohong Wang | Farong Kou

(2024)

Kompleks transfer matris yöntemi ile değişken kesitli bir rotorun titreşim karakteristiğinin analizi ve farklı yöntemlerin karşılaştırılması

Hüseyin Tarık Niş | Ahmet Yıldız

(2024)

Free vibration analyses of 3D printed plates with different geometric fillings: experimental testing and numerical simulations

Ahmet Yildiz | Emre İbram | Onur Erol | Hande Güler Özgül

(2024)

Model Predictive Control of a Multi-Mode Suspension System Using Preview Information and Weight Optimization

Nathan A. Batta | Daniel P. Doscher

(2023)

Fuzzy logic and proportional integral derivative based multi-objective optimization of active suspension system of a 4×4 in-wheel motor driven electrical vehicle

Ömer Bingül | Ahmet Yıldız

(2023)

Structural design optimization of the arc spring and dual-mass flywheel integrated with different optimization methods

Ahmet Yildiz | Önder Yilmaz | Hüseyin Karabulut

(2022)

Optimal Design of a Five-Bar Planar Manipulator and Its Controller by Using Different Algorithms for Minimum Shaking Forces and Moments for the Largest Trajectory in a Usable Workspace

Deniz Kavala Sen | Ahmet Yildiz | Osman Kopmaz

(2022)

Characterization of the torsional vibration behavior of circular and rectangular cross-sectional arc springs: Theory and experiments

Samet Fidanciogullari | Ahmet Yildiz

(2021)

SAE Technical Paper Series

Rong Guo | Shuheng Xu | Ziwei Zhou

(2021)

TEKERLEK İÇİ MOTORLU ELEKTRİKLİ BİR ARACIN AKTİF SÜSPANSİYON SİSTEMİNİN PID VE BULANIK MANTIK TABANLI KONTROLÜ

Mustafa Tayyip TOKSOY | Ahmet YILDIZ

(2020)

Integration design and parameter optimization for a novel in-wheel motor with dynamic vibration absorbers

Qiang Wang | Rui Li | Youfeng Zhu | Xianbin Du | Zongfeng Liu

(2020)

About this article

Received

10 September 2019

Accepted

17 September 2019

Published

30 September 2019

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/vp.2019.21012

Keywords

vehicle vibrations

non-linear

seat

suspension

optimization

PSO

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 09 21

A new design of seat suspension using different models of negative stiffness structure

Huan Yuan, Hongwei Li, Wei Lu

Research article

2021 12 15

PSO optimum control strategy of 7 degrees of freedom semi-active suspensions

Jubin Qiao, Yeonsung Choi, Fuqiang Yang

Research article

2019 08 15

Multi-objective optimization of active suspension predictive control based on improved PSO algorithm

Qiang Zhao, Baoquan Zhu

Research article

2018 09 30

The optimal control of semi-active suspension based on improved particle swarm optimization

Haijing Yan, Jubin Qiao, Sen Zhang, Ting Zhao, Zhongchang Wang

A. Yildiz, “Optimum suspension design for non-linear half vehicle model using particle swarm optimization (PSO) algorithm,” Vibroengineering PROCEDIA, Vol. 27, pp. 43–48, Sep. 2019, https://doi.org/10.21595/vp.2019.21012

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.21012
UR  - https://doi.org/10.21595/vp.2019.21012
TI  - Optimum suspension design for non-linear half vehicle model using particle swarm optimization (PSO) algorithm
T2  - Vibroengineering PROCEDIA
AU  - Yildiz, Ahmet
PY  - 2019
DA  - 2019/09/30
PB  - JVE International Ltd.
SP  - 43-48
VL  - 27
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Yildiz_2019,
	doi = {10.21595/vp.2019.21012},
	url = {https://doi.org/10.21595/vp.2019.21012},
	year = 2019,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {27},
	pages = {43--48},
	author = {Ahmet Yildiz},
	title = {Optimum suspension design for non-linear half vehicle model using particle swarm optimization ({PSO}) algorithm},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]A. Yildiz, “Optimum suspension design for non-linear half vehicle model using particle swarm optimization (PSO) algorithm,” Vibroengineering PROCEDIA, vol. 27, pp. 43–48, Sep. 2019, doi: 10.21595/vp.2019.21012.

Copy IEEE

Copied to clipboard!

Yildiz, Ahmet. “Optimum Suspension Design for Non-Linear Half Vehicle Model Using Particle Swarm Optimization (PSO) Algorithm.” Vibroengineering PROCEDIA 27 (September 30, 2019): 43–48. https://doi.org/10.21595/vp.2019.21012.

Copy Chicago

Copied to clipboard!

Optimum suspension design for non-linear half vehicle model using particle swarm optimization (PSO) algorithm

Abstract

1. Introduction

2. Mathematical model of 5 DOF vehicle

3. PSO optimization algorithms and its procedures

4. Optimization results

5. Conclusions

References

Cited by

About this article

Related Articles