Dynamics analysis of the nonlinear rotor system with Geislinger coupling

Wang, Jinhong; Li, Zhenping; Li, Hongguang; Zhang, Wendi; Bao, Ke

doi:10.21595/vp.2023.23334

Vibroengineering Procedia

Browse Procedia

Published: 18 May 2023

Check for updates

Dynamics analysis of the nonlinear rotor system with Geislinger coupling

Jinhong Wang¹

Zhenping Li²

Hongguang Li³

Wendi Zhang⁴

Ke Bao⁵

^{1, 3, 4}State Key Laboratory of Mechanical System and Vibration, Shanghai Jiaotong University, Beijing, 100072, P. R. China

^{2, 5}China North Vehicle Research Institute, Beijing, 100072, P. R. China

Corresponding Author:

Hongguang Li

Cite the article Download PDF

Downloads 157

Abstract

Rotor systems with coupling consist of two rotors, rolling bearings, sealing components, and nonlinear coupling. Currently, rotor systems with coupling are widely used in marine engines, aerospace engines, and various vehicle engines. In studies of rotor systems with coupling, the coupling connecting both sides of the rotor are often regarded as a linear stiffness unit. But in actual engineering, the torsional stiffness of the coupling varies with the speed of the system, and the variation of the coupling stiffness will affect the dynamic characteristics of the rotor. Based on the above phenomena, this study establishes the rotor model of driveshaft-Geislinger coupling-driveshaft in diesel engines and obtains the modal, frequency, and transient response analysis results of the rotor system with nonlinear Geislinger coupling. The modal, frequency, and transient response analysis results of the nonlinear model are compared with those of the linear model. This study can provide theoretical support for the vibration analysis of nonlinear rotor systems with connected Geislinger coupling.

Dynamics analysis of the nonlinear rotor system with Geislinger coupling

Highlights

A kind of nonlinear driveshaft-Geislinger coupling-driveshaft model for diesel engines and its geometric parameters are proposed. Deriving the torsional vibration equations for the driveshaft-Geislinger coupling-driveshaft model.
Constructing the linear system that differs only in the coupling stiffness. Calculating the modal and frequency response of the nonlinear driveshaft-Geislinger coupling-driveshaft model and comparing the frequency response result of the nonlinear model frequency response with the linear model result.
Providing two different rotor system working conditions. Calculating the transient response of the nonlinear driveshaft-Geislinger coupling- driveshaft model and the linear model at static, 220 Hz, and 300 Hz rotating speeds. Comparison of the trends and peaks in the transient response curves of the nonlinear and linear models at static, 220 Hz, and 300 Hz rotating speeds.
The article concludes the following, the linear model has an error in natural frequency values of the frequency response as the system speed varies. And the natural frequency values of the nonlinear model are generally higher than the linear model. The transient response torsional angle amplitude and curve trend of the model change at static, 220 Hz, and 300 Hz rotating speeds due to the connected stiffness.

1. Introduction

Rotor systems are widely used in vehicles [1, 2], aero-engines [3, 4] and marine engineering [5, 6], where rotor systems with couplings are more common, usually with two rotors on each side, connected by couplings. The coupling reduces the span of the rotor and transmits the torque of both rotors, which plays a key role in the engine. The main relevant studies on the torsional dynamics of rotor systems are: the turbo generator rotor system was accurately predicted by static and dynamic frequency drift simulation analysis [7]. In [8], the authors investigated the harmonic twisting torques dynamic analysis for the torsional vibration of shafts. In [6], the paper calculated the natural torsional vibration mode of marine power transmission systems by two methods. In [9], the torsional vibration of the single rotor-system model was researched, and three markers were placed on the locations of the left and right shaft bearings. In [10], presenting the frequency and active power control method for the wind turbine and diesel engine systems. In these works on the rotor system dynamics, modal, frequency response, and transient response analytical methods are used, and the coupling connecting the two rotors is treated as a linearly constant stiffness. However, the coupling stiffness of a rotor system with connected coupling is nonlinear and varies with the speed of the system [2, 11]. Changing the coupling stiffness will affect the dynamic performance of the connected rotor on both sides, which may cause nonlinear dynamic behaviors such as jump, bi-stable, and combination resonance [12]. Therefore, it is necessary to analyze the dynamics of a rotor system with nonlinear coupling.

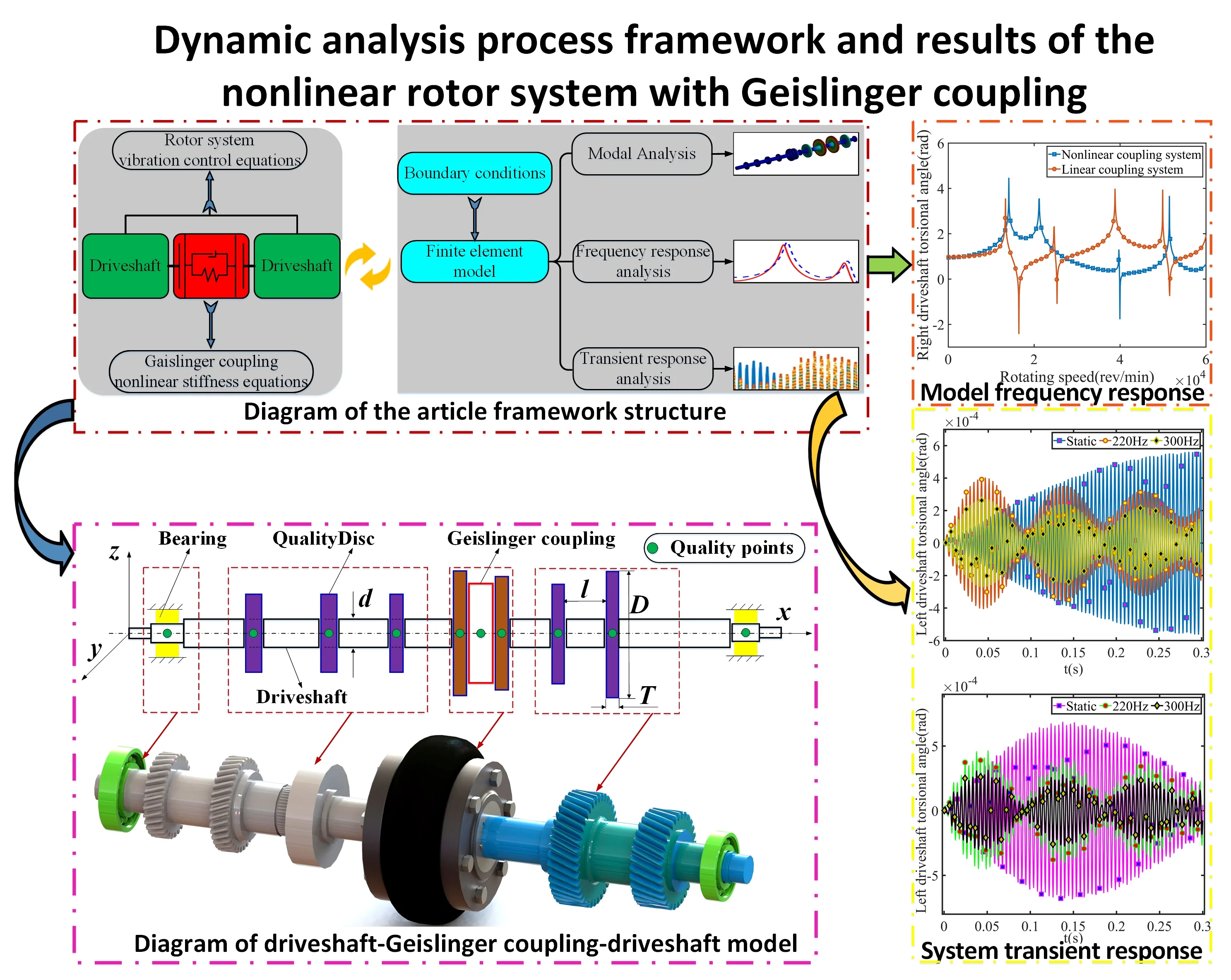
In this study, Section 2 establishes the driveshaft-Geislinger coupling-driveshaft model and provides physical parameters. Section 3 develops the nonlinear coupling stiffness and the torsional vibration equations for the model. In Section 4, the modal, frequency, and transient response analysis results of the model are obtained to compare the differences between the nonlinear and linear results. The effect of the nonlinear stiffness on the transient response is also investigated. Finally, conclusions are given in Section 5. The framework structure of this study is shown in Fig. 1.

Fig. 1Diagram of the article framework structure

2. Driveshaft-Geislinger coupling-driveshaft model

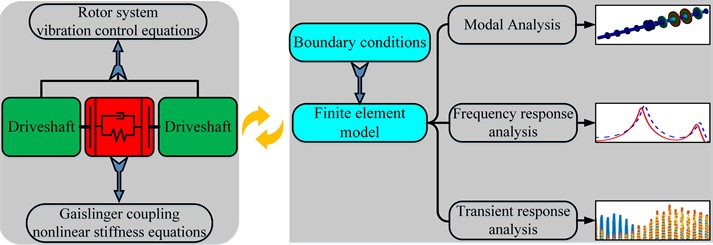
In diesel engines, the commonly used rotor system can be divided into two different driveshaft parts and the Geislinger coupling part, the model is shown in Fig. 2.

Fig. 2Diagram of driveshaft-Geislinger coupling-driveshaft model

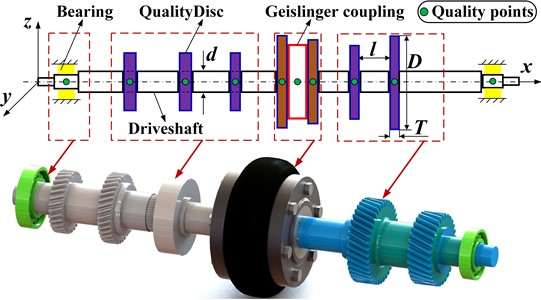
Fig. 2 shows the driveshaft-Geislinger coupling- driveshaft model in the Cartesian coordinate $x y z$ , with the center of the left end of the crankshaft at the origin $o$ . The red frame represents the nonlinear Geislinger coupling, with two driveshafts mounted on both sides. The purple frames represent the quality discs of driveshaft. The yellow frames represent the rolling bearings on the end of the driveshaft. The physical material of the driveshaft-Geislinger coupling-driveshaft model is shown in Table 1.

Table 1Material parameters of the driveshaft-Geislinger coupling-driveshaft system

Parts	Material	Density ( $ρ$ ) kg/m³	Young’s modulus ( $E$ ) 10¹¹MPa	Poisson’s ratio ( $μ$ )
Coupling body	42CrMo	7800	2.06	0.3
Coupling Spring plate	50CrVA	7870	2.09	0.3
Left driveshaft	S275N	7850	2.11	0.3046
Right driveshaft	45#	7850	2.06	0.3

In the analysis, the simplification of nodal torsional stiffness and rotational inertia is necessary, and the equations of torsional stiffness and rotational inertia are as follows [13]:

1

I = \frac{π ρ l d^{4}}{32}, k = \frac{π G d^{4}}{32 l} .

Using Eq. (1), the torsional stiffness and rotational inertia of the system are shown in Table 2.

Table 2Geometric parameters of the driveshaft-Geislinger coupling-driveshaft system

Numbering	Inertia 10^-3kg·m²	Rotational stiffness 10⁶N·m/rad	Length mm	Diameter mm
Driveshaft (1)	20.81	2.94	270	100
Quality disc (2)	76.71	878.01	30	240
Driveshaft (3)	20.03	3.05	260	100
Quality disc (4)	76.71	878.01	30	240
Driveshaft (5)	20.03	3.05	260	100
Quality disc (6)	64.70	740.57	30	230
Driveshaft (7)	24.82	5.28	220	110
Geislinger coupling (8)	40.73	Nonlinear	–	–
Driveshaft (9)	16.18	3.70	210	100
Quality disc (10)	18.22	4612.32	20	330
Driveshaft (11)	11.12	2.32	220	90
Quality disc (12)	23.13	5836.27	20	350
Driveshaft (13)	12.64	2.04	250	90

3. Nonlinear stiffness and system vibration equations

To build the system vibration equation, the Geislinger nonlinear stiffness should be determined:

2

k_{d} = \{\begin{array}{l} k_{s} (1 + 0.37 ω / ω_{0}), & 0 \leq ω \leq ω_{0}, \\ k_{s} (1.1 + 0.27 ω / ω_{0}), & ω_{0} \leq ω, \end{array}

where $ω$ represents system vibration frequency. $k_{s}$ represents the static stiffness of couplings. $ω_{0}$ represents coupling natural frequency [2]. In the oil-filled Geislinger couplings, the damping factor and dynamic damping equation can be expressed as:

3

C_{d} = \frac{κ k_{d}}{ω}, κ = \{\begin{array}{l} (0.02 + 1.1 ω / ω_{0}), & 0 \leq ω / ω_{0} \leq 0.3, \\ (0.2 + 0.5 ω / ω_{0}), & 0.3 \leq ω / ω_{0} \leq 1, \\ 0.7, & ω_{0} \leq ω, \end{array}

where $C_{d}$ represents Geislinger damping. $κ$ represents the damping factor. $ω_{0}$ represents coupling natural frequency.

In this study, the Geislinger coupling type is B41/5/45HC, the coupling static stiffness is $k_{s} =$ 0.329×10⁶ N $∙$ m/rad, coupling natural frequency is $ω_{0} =$ 610 rad/s [14].

For a torsional rotor system with connected coupling, the vibration equation is:

4

I_{x} {\ddot{α}}_{x} + C_{x} {\dot{α}}_{x} + K_{x} α_{x} = T_{x},

where $I$ , $C$ , $K$ , $T$ , and $α$ represent the rotational inertia, nodal damping, torsional stiffness, torsional torque, and torsional angle matrixes respectively.

Taking the components of the nonlinear system into Eq. (4), the equation can be written in:

5

[\begin{array}{l} I_{d l} \\ I_{G} \\ I_{d r} \end{array}] [\begin{matrix} {\ddot{α}}_{d l} \\ {\ddot{α}}_{G} \\ {\ddot{α}}_{d r} \end{matrix}] + [\begin{array}{l} C_{d l} \\ C_{G} \\ C_{d r} \end{array}] [\begin{matrix} {\dot{α}}_{d l} \\ {\dot{α}}_{G} \\ {\dot{α}}_{d r} \end{matrix}] + [\begin{array}{l} K_{d l} \\ K_{G} \\ K_{d l} \end{array}] [\begin{matrix} α_{d l} \\ α_{G} \\ α_{d r} \end{matrix}] = [\begin{matrix} T_{d l} \\ T_{G} \\ T_{d r} \end{matrix}],

where subscript $x$ represents different components of the system, such as $G$ represents Geislinger coupling, $d r$ represents the driveshaft on the right side, and $d l$ represents driveshaft on the left side.

In a rotor system, the magnitude and type of torsional torque to each node subjected differs as the two drive shafts of the system are in different working conditions. This study focuses on harmonic and constant torsional torque, which can be expressed as:

6

T_{i} = \{\begin{array}{l} A_{i} + B_{i} c o s ω_{i} t + C_{i} s i n ω_{i} t, (T o r q u e n o d e s), \\ 0, (N o t o r q u e n o d e s), \end{array}

where $B_{i}$ and $C_{i} =$ 0, $A_{i} \neq$ 0, $T_{i}$ represents the constant torsional torque. When $A_{i}$ , $B_{i}$ and $C_{i} \neq$ 0, $T_{i}$ represents the harmonic torsional torque. When $A_{i}$ , $B_{i}$ and $C_{i} =$ 0, the node is without torque.

In Eqs. (4) and (5), the rotational inertia, nodal damping, and torsional stiffness matrices of the above system are distributed as:

7

I = [\begin{array}{l} I_{n - 1} / 3 & I_{n - 1} / 6 \\ I_{n - 1} / 6 & (I_{n - 1} + I_{n}) / 3 & I_{n} / 6 \\ I_{n} / 6 & (I_{n + 1} + I_{n}) / 3 \end{array}], C = [\begin{array}{l} c_{n - 1} & - c_{n - 1} \\ - c_{n - 1} & c_{n - 1} + c_{n} & - c_{n} \\ - c_{n} & c_{n} \end{array}],

K = [\begin{matrix} k_{n - 1} & - k_{n - 1} \\ - k_{n - 1} & k_{n - 1} + k_{n} & - k_{n} \\ - k_{n} & k_{n} \end{matrix}],

where the rotational inertia is distributed by two energy-distributed inertia matrices. When $n =$ 8, the system torsional stiffness and damping are nonlinear. Taking Eqs. (2), (3), (6) and (7) into Eq. (5) can get a detailed vibration equation for each node of the system.

4. Finite element analysis of the nonlinear model

The finite element model and coordinate in this section use the simplified equivalent model in Fig. 2. According to the material and physical parameters of Table 1 and Table 2, the finite element modal of the driveshaft-Geislinger coupling-driveshaft is established. Modal meshing uses the Cartesian grid, the partition interval size is 0.026 m. The bearing at both ends of the driveshaft is modeled with COMBI214 units, providing the bearing support force in $y$ and $z$ directions. The Geislinger coupling connecting the two drive shafts is simplified with the Torsional Spring function, which inputs the torsional stiffness and torsional damping.

The boundary condition of the driveshaft-Geislinger coupling-driveshaft system is used the Cylindrical Support function, which allows it to only rotate in the $x$ direction, and the remaining five degrees of freedom are restricted. Through the finite element model of the system, the 1st to 8th order natural frequency and modal shapes of the system are calculated, as shown in Table 3.

In Table 3, the 1st and 2nd order modals are integral modal shapes, where the torsional vibration occurs in all mass discs and shaft segments. In the 2nd to 7th order modals, the torsional vibration occurs in the mass discs and shaft segments of the unilateral driveshaft, which is the partial modal shapes. The frequency responses of the nonlinear system and linear system are shown in Fig. 3, and the linear system only differs the connection stiffness, which is $k_{g} =$ 0.25×10⁶ N $∙$ m/rad.

Frequency response analysis of the system speed at 0-2000 Hz (0-12×10⁴rpm), which includes the 1st to 7th order modal shapes. In order to research the transmission effect of the system torsional angle, the sampling point is placed on the first mass disc of the right driveshaft.

Table 3Natural frequencies and Modal shapes of the driveshaft-Geislinger coupling-driveshaft system

Order	Natural frequency (Hz)	Modal shapes	Modal features
1	220.64		Torsional mode of both sides driveshaft
2	302.5		Torsional mode of both sides driveshaft
3	625.31		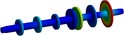Torsional mode of the right-side partial mass disc
4	816.06		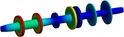Torsional mode of the left-side partial mass disc
5	991.92		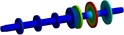Torsional mode of the right-side mass disc
6	1403.1		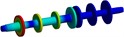Torsional mode of the left-side mass disc
7	1809.7		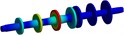Torsional mode of the left-side mass disc
8	5254.8		Torsional mode of the left-side partial shaft

Obviously, the connection stiffness of the nonlinear system increases as the system speed increases, resulting in a change in peak frequencies. In 3rd to 7th order modal shapes, the peak frequencies of nonlinear system (39718 rpm, 51477 rpm, 60360 rpm, 87417 rpm, and 110818 rpm) are higher than linear system (38818 rpm, 49917 rpm, 60960 rpm, 84358 rpm, and 108720 rpm). Such errors in frequency response due to inaccurate connection stiffness are not conducive to understanding the overall vibration characteristics of the system.

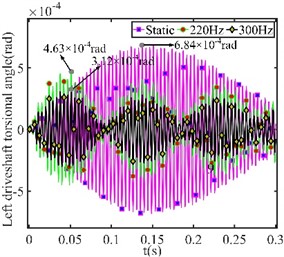
To investigate the effect of nonlinear stiffness on transient response, the transient responses of the system are compared at static, 220 Hz, and 300 Hz rotating speeds. The torsion angle is checked on the mass discs on each side of the system, as shown in Fig. 4.

In the system, the right-side driveshaft has a smaller torsional angle than the left-side driveshaft because the right-side driveshaft needs the connected stiffness for the modal shape transmission. The response peaks of 7.29×10^-4, 5.34×10^-4, and 2.74×10^-4rad on the left-side driveshaft are higher than 5.51×10^-4, 3.96×10^-4, and 2.65×10^-4rad on the right-side. In static state, the connected stiffness is low and the response of the whole system is poorly attenuated. The response amplitude is on the rise in the first 0.3s with no obvious decrease. As the coupling stiffness increases, the torsional transfer effect on both sides is enhanced and the system amplitude fluctuates significantly.

Due to the larger amplitude of the right-side excitation torque, the right-side driveshaft has a larger torsional angle in Fig. 5. The simultaneous application of harmonic torque to both sides driveshaft results the transient response at static showing a significant decrease compared to Fig. 4. In general, the respond trend in the second working condition is consistent with Fig. 4.

Fig. 3Comparison of the linear and nonlinear model frequency response

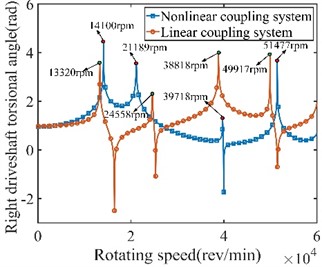
a) Frequency response from 0-6×10⁴rpm

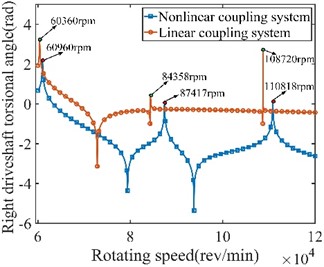
b) Frequency response from 6×10⁴-12×10⁴rpm

Fig. 4System transient response under left-side excitation torque

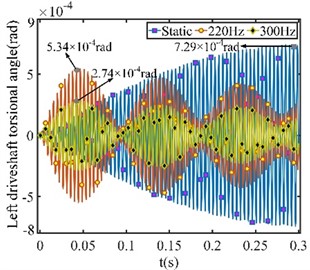
a) Left-side sampling point torsional angle

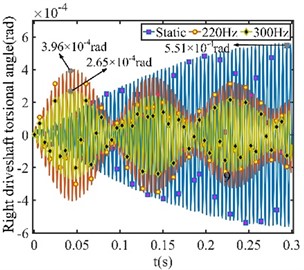
b) Right-side sampling point torsional angle

Fig. 5System transient response under both sides of excitation torque

a) Left-side sampling point torsional angle

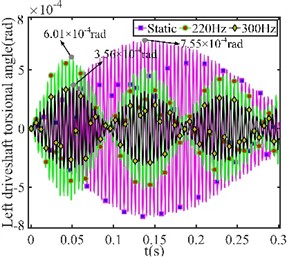
b) Right-side sampling point torsional angle

5. Conclusions

In this study, the torsional vibration equations and finite element analysis of the driveshaft-Geislinger coupling-driveshaft model are provided. Calculating the modalities of the nonlinear model and analyzing the transient response of the nonlinear model at static, 220 Hz, and 300 Hz.

1) The linear model has an error in natural frequency values of the frequency response as the system speed varies. And the natural frequency values of the nonlinear model are generally higher.

2) The transient response amplitude and waveform of the model change at static, 220 Hz, and 300 Hz rotating speeds. The torsional angle of both driveshafts changes due to connected stiffness.

References

H. Zhao, C. Liu, Z. Song, and S. Liu, “Analysis and design considerations of a dual-rotor multiple-winding machine,” IEEE Transactions on Industrial Electronics, Vol. 69, No. 9, pp. 8727–8738, Sep. 2022, https://doi.org/10.1109/tie.2021.3114736

Publisher
S. Fu, N. Luo, H. Huang, Y. Zhou, and W. Ming, “Torsional vibration attenuation characteristics and stiffness identification of flexible coupling in vehicle power train,” Shock and Vibration, Vol. 2020, pp. 1–13, Nov. 2020, https://doi.org/10.1155/2020/8851581

Publisher
L. Hou, Y. Chen, and Y. Chen, “Combination resonances of a dual-rotor system with inter-shaft bearing,” Nonlinear Dynamics, Vol. 111, No. 6, pp. 5197–5219, Mar. 2023, https://doi.org/10.1007/s11071-022-08133-8

Publisher
Y. Li, C. Wen, Z. Luo, and L. Jin, “Dynamic characteristics analysis of a dual-rotor system with bolted-disk joint,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 237, No. 3, pp. 534–548, Feb. 2023, https://doi.org/10.1177/09544062221123988

Publisher
Y. L. Young, “Dynamic hydroelastic scaling of self-adaptive composite marine rotors,” Composite Structures, Vol. 92, No. 1, pp. 97–106, Jan. 2010, https://doi.org/10.1016/j.compstruct.2009.07.001

Publisher
L. Murawski and A. Charchalis, “Simplified method of torsional vibration calculation of marine power transmission system,” Marine Structures, Vol. 39, pp. 335–349, Dec. 2014, https://doi.org/10.1016/j.marstruc.2014.10.004

Publisher
Y. Li, Y. Liu, H. Liu, Q. He, C. Chen, and Y. Yu, “Analysis of torsional dynamic characteristics of turbo-generator rotor based on cross scale modeling method,” Journal of Vibration Engineering and Technologies, Vol. 10, No. 3, pp. 1055–1072, Apr. 2022, https://doi.org/10.1007/s42417-021-00428-1

Publisher
Mohammed Hjaji, Abdurahman Hassen, Hasan Nagiar, and Ezedine Allaboudi, “Exact finite element for torsional vibration of shafts under harmonic torsion,” International Journal of Engineering Research and Technology, Vol. 5, No. 9, Sep. 2016, https://doi.org/10.17577/ijertv5is090300

Publisher
A. I. A. Eisa, L. Shusen, and W. M. K. Helal, “Study on the lateral and torsional vibration of single rotor-system using an integrated multi-body dynamics and finite element analysis,” Advances in Mechanical Engineering, Vol. 12, No. 10, p. 168781402096833, Oct. 2020, https://doi.org/10.1177/1687814020968336

Publisher
M. Shojaee and S. M. Azizi, “Decentralized robust control of a coupled wind turbine and diesel engine generator system,” IEEE Transactions on Power Systems, Vol. 38, No. 1, pp. 807–817, Jan. 2023, https://doi.org/10.1109/tpwrs.2022.3167627

Publisher
Y. Li, “Dynamic analysis of torsional vibration of reed damper of diesel engine,” in Journal of Physics: Conference Series, Vol. 1300, No. 1, p. 012050, Aug. 2019, https://doi.org/10.1088/1742-6596/1300/1/012050

Publisher
Y. Li, Z. Luo, J. Liu, H. Ma, and D. Yang, “Dynamic modeling and stability analysis of a rotor-bearing system with bolted-disk joint,” Mechanical Systems and Signal Processing, Vol. 158, p. 107778, Sep. 2021, https://doi.org/10.1016/j.ymssp.2021.107778

Publisher
Z. Chen et al., “Research on power enhancement of TCD2015V08 diesel engine based on one-dimensional simulation and analysis,” in IOP Conference Series: Earth and Environmental Science, Vol. 208, p. 012009, Dec. 2018, https://doi.org/10.1088/1755-1315/208/1/012009

Publisher
“Geislinger Coupling.”. https://www.geislinger.com

Search CrossRef

About this article

Received

19 April 2023

Accepted

04 May 2023

Published

18 May 2023

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2023.23334

Keywords

nonlinear rotor system

Geislinger coupling

dynamic characteristics

finite element model

modal and harmonic response

Acknowledgements

This work is supported by the National Natural Science Foundation of China under No. 11972222 and the Equipment Pre-research Common Technology Foundation of China under No. 50910050302.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 08 25

Nonlinear dynamic characteristics analysis of a rotor system supported on aerodynamic bearings

Yao Fu, Fei Wang

Research article

2017 05 15

Research on modeling and dynamic characteristics of complex coaxial rotor system

Fei Wang, Gui-Huo Luo, Xi-Guan Yang, Hai-Tao Cui

Research article

2017 02 15

A dynamic modeling method for helical gear systems

Ming Yan, Hong-quan Liu

Research article

2015 12 30

Nonlinear dynamic analysis for high speed gear-rotor-bearing system of the large scale wind turbine

Shihua Zhou, Guiqiu Song, Mengnan Sun, Zhaohui Ren

J. Wang, Z. Li, H. Li, W. Zhang, and K. Bao, “Dynamics analysis of the nonlinear rotor system with Geislinger coupling,” Vibroengineering PROCEDIA, Vol. 49, pp. 73–79, May 2023, https://doi.org/10.21595/vp.2023.23334

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2023.23334
UR  - https://doi.org/10.21595/vp.2023.23334
TI  - Dynamics analysis of the nonlinear rotor system with Geislinger coupling
T2  - Vibroengineering PROCEDIA
AU  - Wang, Jinhong
AU  - Li, Zhenping
AU  - Li, Hongguang
AU  - Zhang, Wendi
AU  - Bao, Ke
PY  - 2023
DA  - 2023/05/18
PB  - JVE International Ltd.
SP  - 73-79
VL  - 49
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Wang_2023,
	doi = {10.21595/vp.2023.23334},
	url = {https://doi.org/10.21595/vp.2023.23334},
	year = 2023,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {49},
	pages = {73--79},
	author = {Jinhong Wang and Zhenping Li and Hongguang Li and Wendi Zhang and Ke Bao},
	title = {Dynamics analysis of the nonlinear rotor system with Geislinger coupling},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]J. Wang, Z. Li, H. Li, W. Zhang, and K. Bao, “Dynamics analysis of the nonlinear rotor system with Geislinger coupling,” Vibroengineering PROCEDIA, vol. 49, pp. 73–79, May 2023, doi: 10.21595/vp.2023.23334.

Copy IEEE

Copied to clipboard!

Wang, Jinhong, Zhenping Li, Hongguang Li, Wendi Zhang, and Ke Bao. “Dynamics Analysis of the Nonlinear Rotor System with Geislinger Coupling.” Vibroengineering PROCEDIA 49 (May 18, 2023): 73–79. https://doi.org/10.21595/vp.2023.23334.

Copy Chicago

Copied to clipboard!

Dynamics analysis of the nonlinear rotor system with Geislinger coupling

Abstract

Highlights

1. Introduction

2. Driveshaft-Geislinger coupling-driveshaft model

3. Nonlinear stiffness and system vibration equations

4. Finite element analysis of the nonlinear model

5. Conclusions

References

About this article

Related Articles