Health diagnosis of marine engine room equipment based on BP and D-S evidence theory

2.1. BP neural network

BP neural network is a kind of multilayer feedforward neural network, including input layer, hidden layer and output layer. There are two kinds of signal, function signal and error signal, in the forward and back propagation of the network. In forward transmission, the input sample is processed layer by layer through each hidden layer until the output layer. When the output does not conform to the expectation, it turns into error backpropagation, which transmits the output back to the input layer layer by layer through the hidden layer and distributes the error to all units of each layer, so as to obtain the error signal of units of each layer and adjust the weight of each unit [2]. The structure of BP neural network is shown in Fig. 1.

Fig. 1Structure of BP neural network

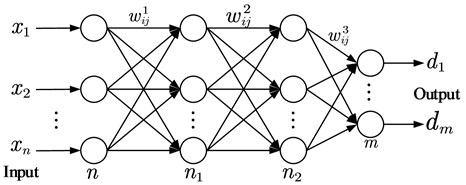
In the BP neural network, assume that the input vector is dimension $n$ vector ${x=[x_1,x_2,\dots ,x_n]}^T$, and the expected output is $D=[d_1,d_2,\dots ,d_n]$, Calculate the output of the network under $x$ input:

Correct the weights with the following formula: ${\omega }_{ij}^l(t+1)={\omega }_{ij}^l\left(t\right)+\mathrm{\Delta }{\omega }_{ij}^l\left(t\right)$, $j=\mathrm{1,2},\cdot \cdot \cdot ,n_{l-1}$ until the output is as expected.

2.2. D-S evidence theory

Evidence theory is a kind of uncertainty reasoning method. It transforms the uncertainty of propositions into the uncertainty of sets, and forms the mathematical theory of evidence deduction. It provides a powerful tool for the representation and fusion of uncertain information at decision level [3]. Under the identification framework $U$, function $m$ is defined, if function $m:2^U\to \left[\mathrm{0,1}\right]$ satisfies:

I call it $A$ function of $m$ defined on $U$. The set function $m\left(A\right)$ is the confidence given to subset $A$ itself. Define confidence function: if function $Bel:2^U\to \left[\mathrm{0,1}\right]$ satisfies:

I call it $A$ confidence function defined on $U$. Set function $Bel\left(\mathrm{A}\right)$ means that confidence is assigned to the subset and all subset $A$, $Bel\left(A\right)$ is the sum of the probability measures of all subsets of $A$. Suppose ${Bel}_1$, ${Bel}_2$ is two trust functions under the same recognition framework, and $m_1$, $m_2$ assigns values to their corresponding basic probabilities respectively, then $m=m_1\oplus m_2$ is:

where, symbol $\oplus$ represents Dempster combination rule; $K$ is the normalization factor, after generating the combined quality function, the corresponding confidence function and likelihood function can be further obtained, so as to obtain the combined confidence interval and complete the reasoning of evidence.

3.1. Construction based on feature vector of time domain parameters

In the fault diagnosis of engine room equipment, the basic digital characteristics of time domain signals and their probability distribution characteristics are generally used for analysis and diagnosis. Through the analysis and recognition of vibration signal time domain waveform, can effectively distinguish the failure of mechanical equipment, Digital filtering is performed on the original vibration time domain signal ${\{x}_i\}$, $i=\mathrm{1,2},3,\dots ,N$ collected, and the calculation formula of the dimensionless characteristic parameters extracted in the time domain is shown in Table 1[4].

Select the dimensional and non dimensional parameters in the time domain information to construct the real-time monitoring eigenvector of vibration acceleration: $T_A=\left[X_{rms},X_P,L,S,I,C,K\right]$.

The feature vector contains rich information on vibration state, which can comprehensively reflect the amplitude and energy of time-domain vibration and the time-series distribution of time-domain signals. When it changes weakly, the vibration state will be greatly different [5].

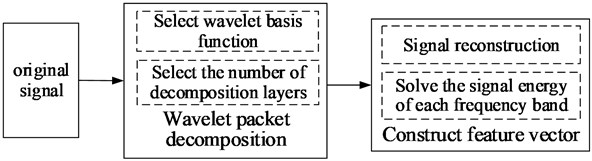
3.2. Feature vector construction based on wavelet packet decomposition

Wavelet packet is an important part of wavelet analysis theory, which is widely used in non-stationary signal feature detection and fault diagnosis. Wavelet packet transform has higher frequency resolution and lower time resolution in the low frequency part, and higher time resolution and lower frequency resolution in the high frequency part. When different faults occur, the wavelet packet energy distribution of the vibration signal of the equipment is different. The corresponding energy at the fault characteristic frequency is large, while the energy at other frequencies is small. Therefore, after the wavelet packet is decomposed into several frequency bands, the energy in each frequency band can represent the failure of the equipment [6].

The wavelet packet in frequency domain is decomposed into three layers and eight bands. eight parameters of energy in each frequency band of wavelet decomposition are calculated to form energy feature vector $E_A$ Energy calculation formula $E_{i,j}$ is as follows:

where, $x_{i,j}^k$ ($j=$1, 2,…, $2^{i-1}$, $k=$1, 2,…, $m$) is the amplitude of discrete points of reconstructed signals in each frequency band, $m$ is the node value of wavelet packet in layer $i$, and the feature vector $E_A$ is constructed based on the relative energy parameters of each frequency band after wavelet decomposition:

where, $E_A$ is the normalized feature vector of $A$ single sample, and $E_j$ is $j$ reconstructed signals of the third layer.

Fig. 2Wavelet decomposition process

4.1. Experimental data set

In order to verify the effectiveness of the fault diagnosis method combined with BP neural network and evidence theory, data collected by the driver accelerometer in the rolling bearing data collection of Western Reserve University bearings DE, he normal reference data of Normal_0, inner ring fault IR007_0, rolling body fault B007_0 and outer ring fault OR007@6_0 of the motor at 1797 rpm were selected [7].

After the data is imported, the vibration data is preprocessed by filtering and denoising, and the data is divided into 4096 data points as an example. 40 feature vectors of normal data and 120 feature vectors of inner ring fault, rolling body fault and outer ring fault were constructed. A total of 400 sample data were collected. Then, the time domain characteristic parameters are extracted to construct the time domain characteristic parameter vector $X_A$; Then, the multilayer wavelet transform is applied to the signal, and the energy value of each frequency band is extracted to construct the energy characteristic parameter vector $E_A$of the wavelet packet. Finally, the samples were randomly divided into 360 training sets and 40 test sets.

After sample division, two BP neural networks are established for fault diagnosis of time domain characteristic parameters and wavelet packet energy respectively. In order to improve the accuracy of diagnosis, D-S is used for decision level fusion diagnosis, and the fault diagnosis model is shown in Fig. 3.

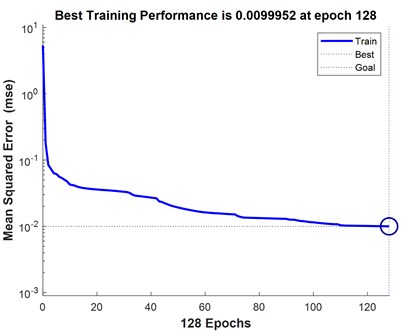
The normalized samples are trained in BP neural network, considering moderate computational complexity and short simulation time. It is very important to choose $n=2\mathrm{*}M-1$ reasonable hidden layer structure. According to the empirical formula A for the number of hidden layer nodes, there are $n=15$ and $n=13\mathrm{}$. Then gradually test the number of nodes in the hidden layer, and find that the performance is the best when the number of nodes is 19 and 16. The neural network error variation diagram is shown in Fig. 4.

Fig. 3Fault diagnosis model

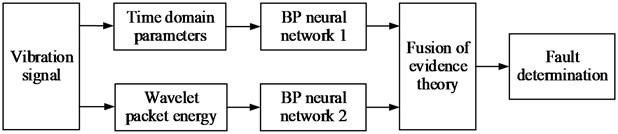
Fig. 4Error variation diagram of networks 1 and 2

4.2. Research and analysis of results

According to the output results of neural network, the identification framework of fault diagnosis is established: $\theta =\{A_1,A_2,A_3,A_4\}$, where $A_1$ is in normal state, $A_2$is the inner ring failure, $A_3$ is the fault of the rolling body, $A_4$ is the outer ring fault, Then the construction of BP neural network evidence body $E=\{E_1,E_2\}$, $E_1$, $E_2$are the evidence bodies constructed by network 1 and Network 2 respectively. Then determine the trust allocation function in identification frame $\theta$ [8]. The basic probability distribution of each evidence body is shown in Table 2. Finally, the diagnosis results are fused according to D-S evidence theory, and the basic probability distribution and diagnosis results obtained are shown in Table 3.

4.3. Accuracy analysis

After obtaining the classification results of time domain characteristic parameters and wavelet packet energy, in order to intuitively display the fusion effect of D-S evidence theory, the prior information is counted and fault classification is made as shown in Figs. 5-6.

Fig. 5Time domain and wavelet statistical classification diagram

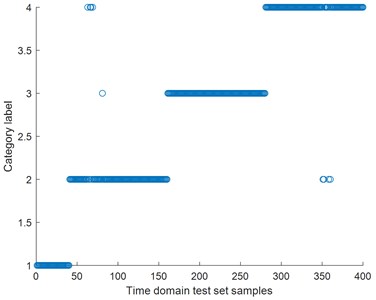
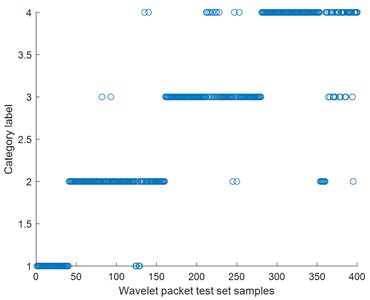
Fig. 6D-S fusion statistical classification diagram

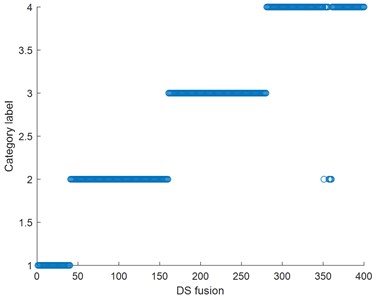
Combining the above classification diagram, calculate the time domain, the wavelet analysis and evidence fusion accuracy, as shown in Table 4, through the data contrast, overall fault diagnosis of bearing, the time domain analysis of accuracy is higher than the accuracy of wavelet analysis, after D-S fusion, fault classification accuracy than single time domain or wavelet analysis to better [9].