Fault diagnosis method of gear based on lifting wavelet packet and combined optimization BP neural network

2.1. Non-sampling lifting wavelet packet decomposition algorithm

Firstly, the initial prediction operator and the update operator are obtained by the Lagrange interpolation subdivision principle. Let the initial prediction operator $P=｛p_m｝$, where $m=$1, 2,…, $N$. Set the initial update operator $U=｛u_n｝$, where $n=$1, 2,…, $\tilde{N}$. The expression of the $s$-layer non-sampling lifting wavelet packet prediction operator $P^{\left[s\right]}$and the update operator $U^{\left[s\right]}$ as follow [7]:

Compared with the traditional lifting wavelet packet decomposition process, the non-sampling lifting wavelet packet removes the segmentation link and performs the operation in a non-sampling manner. Let $X_{sl}$be the first frequency band signal of the original signal $X$ decomposed in the s layer. Each sample of the upper layer signal $X_{s-1}$ is predicted by the adjacent $2^{s}N$ sample signals by the non-sampling predictor $P_i^{\left[s\right]}$, and the predicted difference is the high-frequency detail signal $X_{s\left(l-1\right)}$, such as Eq. (2). The low-frequency approximation signal $X_{sl}$ is obtained by updating the detail signal by the non-sampling prediction operator $u_j^{\left[s\right]}$, as given by Eq. (3):

In the Eqs. (2)-(3), $l=$2, 4, 6, ..., 2$s$, $P_i^{\left[s\right]}$ is the non-sampling boost wavelet packet prediction operator coefficient of detail signal $X_{s\left(l-1\right)}$, and $u_j^{\left[s\right]}$ is the non-sampling boost wavelet packet update operator coefficient of approximating signal $X_{sl}$.

2.2. Non-sampling lifting wavelet packet reconstruction algorithm

The non-sampling lifting wavelet packet reconstruction algorithm is the inverse operation of the above decomposition algorithm, which consists of a recovery update link, a recovery prediction link and a merge link. The recovery update is performed by the signals $X_{sl}$ and $X_{s\left(l-1\right)}$to complete the recovery of the sample sequence $X_{\left(s-1\right)\left(l/2\right)}^{*}$, as shown in the Eq. (4). The recovery prediction link is recovered by the signal $X_{s\left(l-1\right)}$ and the completed sample sequence $X_{\left(s-1\right)\left(l/2\right)}^{**}$, as shown in Eq. (5). The merged link is obtained by averaging the signal $X_{\left(s-1\right)\left(l/2\right)}^{*}$ and $X_{\left(s-1\right)\left(l/2\right)}^{**}$ adding, is given us by Eq. (6), and the result is the non-sampling lifting wavelet packet reconstructed signal $X_{\left(s-1\right)\left(l/2\right)}$:

3.1. GA optimizes the topology and network parameters of BP-NN

GA optimizes the topology and network parameters of BP-NN as follows:

Step 1: Assume the number of hidden layers and nodes between the layers in the BP-NN. The number of layers and nodes are encoded to randomly generate N encoded chromosomes.

Step 2: Decode the $N$ encoded chromosomes into corresponding BP-NNs.

Step 3: Train each network separately with different initial weights.

Step 4: Calculate the error function of BP-NN under each code string separately, and use the error function to determine the fitness function of every individual. GA optimizes the network topology to minimize the sum of squared errors in the network output, but GA can only evolve in the direction of increasing the fitness function value. Therefore, the inverse of the squared sum of the BP-NN output error is chosen as the fitness function, as follows Eq. (7):

where $p$ is the number of training samples, $i$ is the number of network output nodes, $\widehat{y}\left(p\right)$ is the expected output value of the network, the current output value of the network, $E_J$ is called the evolution error, and $Fit$ is the fitness value.

Step 5: Calculate the fitness value according to Eq. (7), and select a plurality of individuals with large fitness values to form a male parent.

Step 6: The current generation of populations are manipulated by genetic operators such as crossover and mutation to produce a new generation of populations.

Step 7: Repeat steps Step 2-Step 6 until an individual in the group can meet the network requirements.

3.2. The improved BP-NN theory of LM algorithm

The LM algorithm applies the approximate second-order derivative information, which is a combination of the descending gradient algorithm and the Gauss-Newton algorithm. It has the local characteristics of Newton’s method, can generate an ideal search direction near the optimal value, and has the global characteristics of the gradient method. That is, the steps that just started the iteration drop faster. Therefore, the convergence rate is faster and more stable than the falling gradient algorithm [9]. The expression of the iteration of the LM algorithm is:

where:

where $x\left(k\right)$ is the vector of the weight and threshold of the $k$th iteration, $e_i\left(x\right)$ is the error of the $i$th network node, $i$ is the identity matrix, $J\left(x\right)$ is called the Jacobian matrix, $\mu$ is one greater than zero adaptive adjustment factor.

When $\mu \to$ 0, $\mu I\approx$0, $∆x=-{\left(J^T\left(x\right)J\left(x\right)\right)}^{-1}{J}^T\left(x\right)e\left(x\right)$, and Eq. (8) becomes Eq. (9), namely, Gauss Newton algorithm:

When $\mu \to \infty$, $J^T\left(x\right)J\left(x\right)\ll \mu I$, $J^T\left(x\right)J\left(x\right)$ are negligible, the LM algorithm is transformed into a gradient descent method. The LM algorithm can better achieve the combination of Gauss-Newton method and gradient descent method by adaptively adjusting $\mu$. Practice has shown that the LM algorithm is dozens or even hundreds of times faster than the falling gradient method. At the same time, the LM algorithm is positively defined, and there is always a solution. However, it is not necessary for the Gauss-Newton method $\left(J^T\right(x\left)J\right(x)+\mu I{)}^{-1}$ to be full rank. The LM algorithm is better than the Gauss-Newton me

4.1. Fault signal acquisition

The hardware involved in the experimental device mainly includes QPZZ-II rotating mechanical vibration analysis and fault diagnosis test platform system, one signal conditioning instrument, two data collectors, and several acceleration sensors. The schematic diagram of the experimental platform in Fig. 1. The pinion of the experimental platform is a driving wheel, which relates to the motor shaft. the large gear is a driven wheel, and is connected to the magnetic powder brake through a coupling. The number of teeth of the pinion gear is 55, and the number of teeth of the large gear is 75. The two accelerometers are installed in the horizontal and vertical directions at the large gear on the outer side of the gearbox. The calibration values of the two sensors are 102 mV/g and 99 mV/g, respectively. The measuring point arrangement as shown in Fig. 2.

Fig. 1The experimental platform

Fig. 2Sensor test point arrangement

4.2. Diagnosis results

Based on obtaining four kinds of vibration signals: normal signal, gear broken tooth, gear crack and wear, the method proposed in this paper is used to realize the diagnosis of various gear fault types. The specific diagnosis steps are as follows:

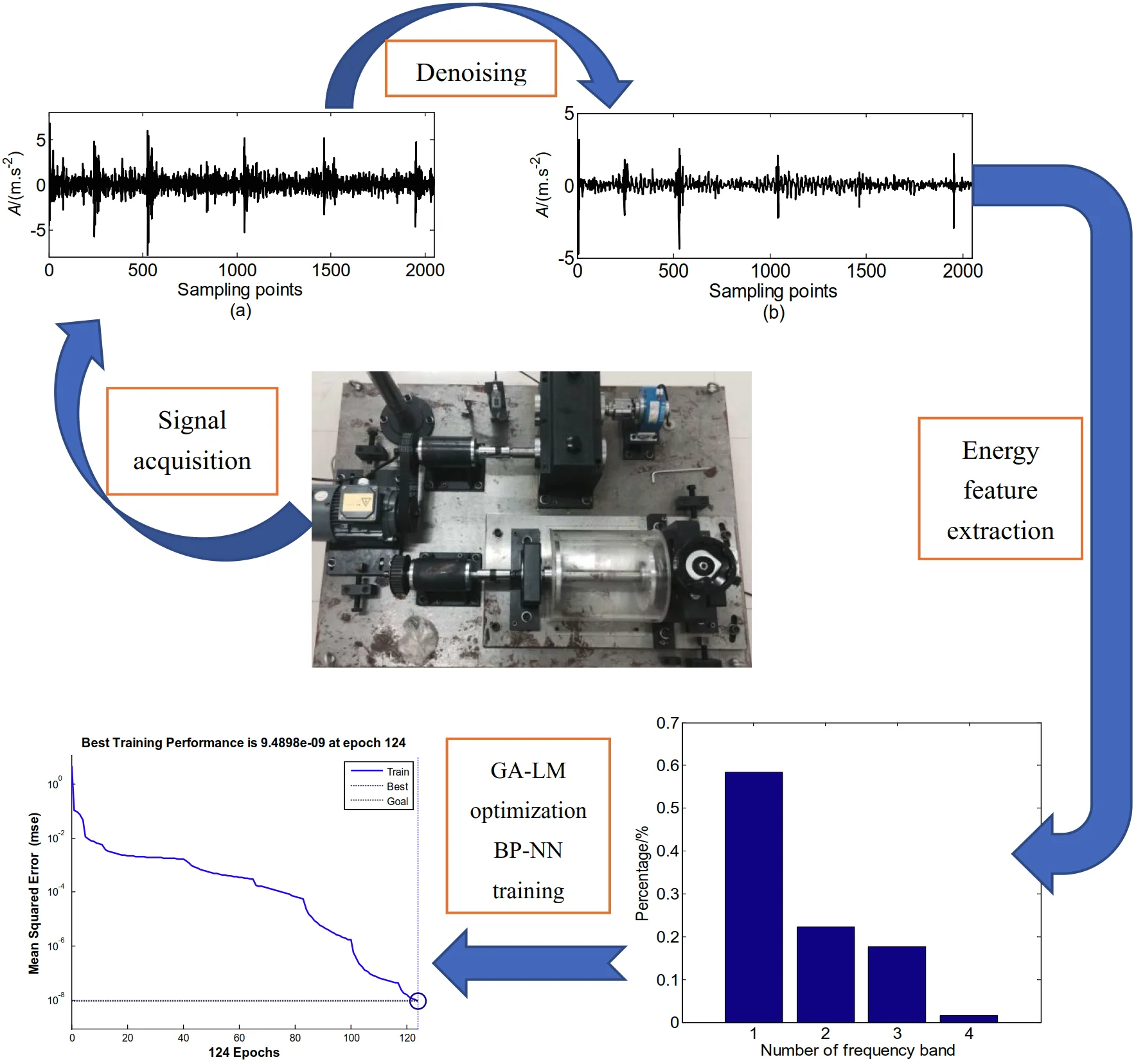
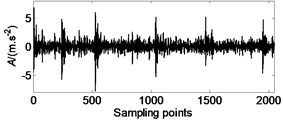
(1) Using the redundant lifting wavelet packet method to denoise the broken gear teeth, gear surface cracks and wear signals, as depicted in Fig. 3.

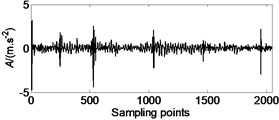
(2) Calculate the energy characteristics of the signals of each frequency band decomposed by the wavelet packet and normalize them. Fig. 4 is the energy spectrum of the broken teeth.

(3) Establish BP-NN network by using GA optimization BP-NN topology and network parameters.

Fig. 3Broken teeth noise reduction effect: a) the original signal of gear fault; b) the signal denoised of gear fault by redundant lifting scheme packet

a)

b)

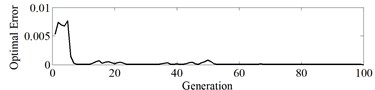
The input sample of BP-NN is the fault energy characteristic vector of the gear, and the output is of four fault types: no fault (1,0,0,0), gear tooth breaking fault (0,1,0,0), gear surface Crack failure (0,0,1,0), gear wear (0,0,0,1). Therefore, there are 8 nodes in the input layer and 4 nodes in the output layer. Set the population number to 50, the maximum running algebra to 100, and the generation gap to 0.9. The error reduction curve of the optimization process is in Fig. 5. After the topology of the neural network is established, the initial weight and threshold parameters of the GA optimization network are continuously used. Fig. 6 is the error reduction curve, the error square curve and the fitness curve of the parameter optimization process.

Fig. 4Signal failure energy spectrum distribution

Fig. 5Error reduction curve

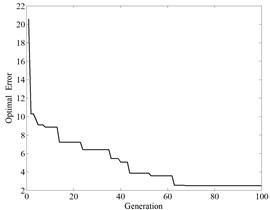
Fig. 6Error and fitness curve

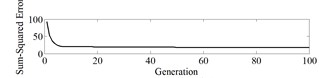
a) Error sum of squares curve

b) Fitness curve

c) Optimization error descent curve

(4) Using LM algorithm to improve the efficiency of BP-NN search target, set the transfer function of hidden layer and output layer to tansig and purelin respectively, and the minimum mean square error index is set to 10^-5.

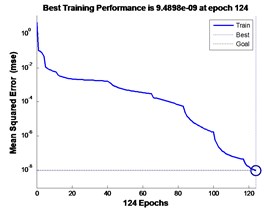
The results show that the GA-optimized BP-NN needs to iterate 199 steps to reach the set mean square error index, as shown in Fig. 7. 45 cases were successfully diagnosed in 50 test samples, and the cumulative error of the four types of faults was 0.0093. After GA-LM combination optimization, BP-NN only needs to iterate 124 steps to reach the set mean square error index, as shown in Fig. 8, successfully diagnosed 47 For example, the cumulative error of the four fault types is 0.0078. Therefore, the combined optimization BP-NN converges faster, namely, the diagnosis time is shorter and the diagnostic accuracy is higher.

Fig. 7GA optimization BP-NN training process

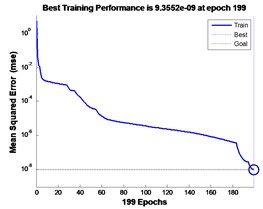
Fig. 8GA-LM optimization BP-NN training process