Bearing fault diagnosis method based on EEMD and adaptive redundant lifting scheme packet

Su, Hongtao; Song, Mengmeng; Xiong, Zicheng

doi:10.21595/vp.2020.21733

Vibroengineering Procedia

Browse Procedia

Published: 05 November 2020

Check for updates

Bearing fault diagnosis method based on EEMD and adaptive redundant lifting scheme packet

Hongtao Su¹

Mengmeng Song²

Zicheng Xiong³

¹Office of the General Manager, Shanghai Jili Transmission Technology Co., Ltd., Shanghai, People’s Republic of China

²College of Information, Mechanical and Electrical Engineering, Ningde Normal University, Ningde, People’s Republic of China

³School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, People’s Republic of China

Corresponding Authors:

Hongtao Su, Mengmeng Song

Cite the article Download PDF

Downloads 837

CrossRef Citations 4

Abstract

In this work, a novel bearing fault diagnosis method based on EEMD and adaptive redundant lifting scheme packet is proposed. Firstly, EEMD method is used to decompose rolling bearing signals of different fault types, and the correlation coefficient criterion method is carried out in order to screen effective IMF components and reconstruct them. Then, the adaptive redundant lifting scheme packet method is used to denoise the reconstructed signal, and the energy characteristics of different fault signals are extracted. Finally, the bearing fault diagnosis system is constructed by BP neural network diagnosis. The results show that the diagnostic method proposed in this paper has better diagnosis efficiency and precision than the traditional wavelet packet.

Highlights

A bearing fault diagnosis method based on EEMD and adaptive redundant lifting scheme packet is proposed.
BP neural network based on redundant lifting scheme packet is built.
The diagnosis results of BP neural network show that the proposed diagnosis method has higher diagnosis accuracy and efficiency than the traditional wavelet packet.

1. Introduction

Rolling bearing is one of the most widely used components and parts in rotating machinery. It has the function of bearing load and relative motion. Its running state is directly related to the performance and life of the whole equipment[1, 2]. Although wavelet packet transform has multi resolution capability to decompose high and low frequency signals in bearing fault diagnosis. However, wavelet packet transform takes a preset single wavelet function as the basis function of signal decomposition, so it can't carry out adaptive analysis according to the characteristics of the signal. Secondly, due to the sampling operation of wavelet packet transform, the length of each frequency band during signal decomposition is only 1/2 of the signal length before decomposition. The more levels of decomposition, the amount of information carried by each frequency band signal is reduced layer by layer, and the time resolution is reduced, thus the signal distortion is easy to occur [3]. In addition, the decomposition result of sampling operation is translational variable, which is easy to cause frequency aliasing.

In response to the above problems, this paper is on the basis of literature [4], based on the EEMD (Ensemble Empirical Mode Decomposition, EEMD) and adaptive redundant lifting scheme packet bearing fault diagnosis method, through non-sampling operation, keeping the signal length of each frequency band consistent with the initial signal length, effectively retaining the impact component information in the bearing signal, make the information redundant, achieve the purpose of accurately extracting the frequency of rolling bearing faults, and successfully realize the diagnosis of such faults.

2. Brief introduction to the principle of the diagnosis plan

2.1. EEMD principle

EEMD is an improved method of EMD, which is based on the decomposition of the data itself and does not need to set the basis function in advance, which makes the instantaneous frequency of each component have physical significance, and also avoids the modal aliasing between components. EEMD makes use of the characteristic of uniform frequency distribution of Gaussian white noise to make the decomposition scale of noisy signal uniformly distributed and suppress impulse interference; meanwhile, it changes the characteristics of signal extreme points to make the signal continuous in different scales.

The process of EEMD decomposition is as follows [5, 6].

Step 1: Add $N$ times of Gaussian white noise $ω_{i} (t)$ with a mean value of zero and a constant standard deviation to the input signal $x (t)$ , construct the initial signal $x_{i} (t)$ , namely:

1

x_{i} (t) = x (t) + ω_{i} (t) .

Step 2: Perform EMD decomposition of the initial signal $x_{i} (t)$ to obtain $l$ intrinsic modal function IMF components and a remaining item $r_{i} (t)$ :

2

x_{i} (t) = \sum_{j = 1}^{l} y_{i j} (t) + r_{i} (t),

where $y_{i j} (t)$ is the $j$ -th IMF component generated by EMD decomposition after adding Gaussian white noise for the $i$ -th times.

Step 3: calculate the mean value of each IMF component $y_{i j} (t)$ to obtain the IMF component $y_{j} (t)$ and remaining items $r (t)$ . This step can reduce or even eliminate the impact of the joined $ω_{i} (t)$ on the IMF:

3

y_{j} (t) = \frac{1}{N} \sum_{i = 1}^{N} y_{i j} (t),

4

r (t) = \frac{1}{N} \sum_{i = 1}^{N} r_{i} (t),

where, $y_{j} (t)$ is the $j$ -th IMF component obtained after EEMD decomposition of signal $x (t)$ .

Therefore, the signal $x (t)$ decomposed by EEMD can be composed of $l$ $y_{j} (t)$ and $a$ $r (t)$ , as shown in Eq. (5):

5

x (t) = \sum_{j = 1}^{l} y_{j} (t) + r (t) .

3. Decomposition and reconstruction algorithm of adaptive redundant lifting scheme packet

Compared with the sampling lifting wavelet packet[7, 8] decomposition process, the method of this paper eliminates the subdivision link and uses non sampling method for operation. Let $X_{s l}$ be the $l$ -th frequency band signal decomposed by the original signal $X$ at the $s$ layer. Each sample of the upper layer signal $X_{s - 1}$ is predicted by adjacent $2^{s} N$ sample signals through the non sampling prediction operator ${p_{i}}^{[s]}$ , and the predicted difference is the high-frequency detail signal $X_{s (l - 1)}$ , as shown in Eq. (6). The low-frequency approximation signal $X_{s l}$ is obtained by updating the detail signal by the nonsampling prediction operator $U_{j}^{[s]}$ . The expression is shown in Eq. (7) [4]:

6

X_{s (l - 1)} (k) = X_{(s - 1) (\frac{l}{2})} (k) - \sum_{i = 1}^{2^{s} N} \{{p_{i}}^{[s]} X_{(s - 1) (\frac{l}{2})} [k - 2^{(s - 1)} (N + 1) + i]\},

7

X_{s l} (k) = X_{(s - 1) (\frac{l}{2})} (k) + \sum_{j = 1}^{2^{s} \tilde{N}} \{{u_{j}}^{[s]} X_{s (l - 1)} [k - 2^{(s - 1)} (\tilde{N} + 1) + j]\} .

In the equation, $l =$ 2, 4, 6,…, $2^{s}$ , ${p_{i}}^{[s]}$ is the adaptive redundant lifting scheme packet prediction operator coefficient of the detail signal $X_{s (l - 1)}$ , and ${u_{j}}^{[s]}$ is the adaptive redundant lifting scheme packet update operator coefficient of the approximation signal $X_{s l}$ .

The reconstruction process of adaptive redundant lifting scheme packet is the inverse operation of the above decomposition process, including updating, predicted recovery and merging. The expressions of these three links are shown in Eq. (8) to Eq. (10):

8

{X^{*}}_{(s - 1) (\frac{l}{2})} (k) = X_{s l} (k) - \sum_{j = 1}^{2^{s} \tilde{N}} \{{u_{j}}^{[s]} X_{s (l - 1)} [k - 2^{(s - 1)} (\tilde{N} + 1) + j]\},

9

{X^{* *}}_{(s - 1) (\frac{l}{2})} (k) = X_{s (l - 1)} (k) + \sum_{i = 1}^{2^{s} N} \{{p_{i}}^{[s]} {X^{*}}_{(s - 1) (\frac{l}{2})} [k - 2^{(s - 1)} (N + 1) + i]\},

10

X_{(s - 1) (\frac{l}{2})} (k) = \frac{1}{2} [{X^{*}}_{(s - 1) (\frac{l}{2})} (k) + {X^{* *}}_{(s - 1) (\frac{l}{2})} (k)] .

4. Experimental results and analysis

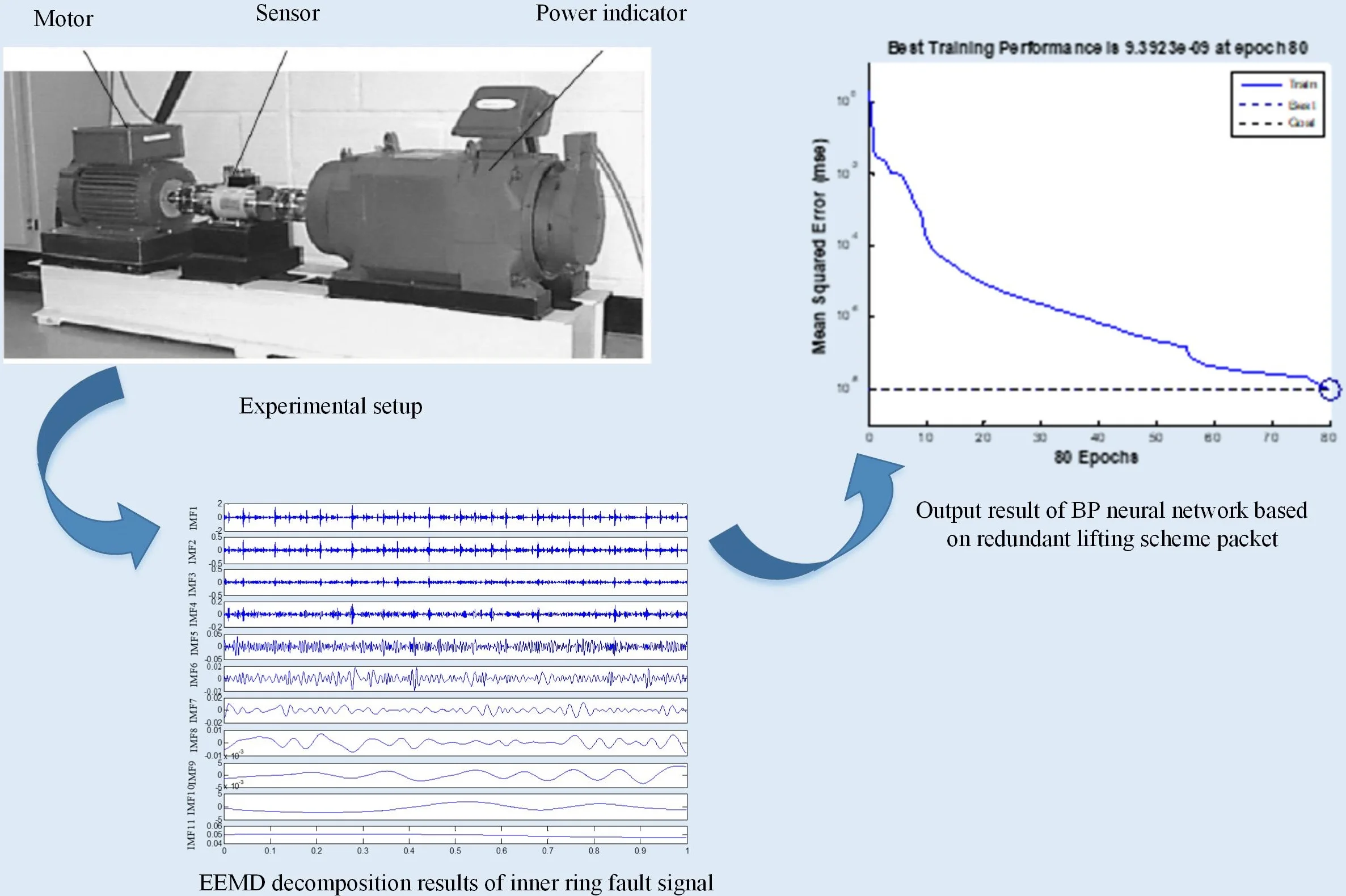
4.1. Experimental setup

The type of fault simulation bearing used in the experiment is fan end deep groove ball bearing SKF-6203, the number of rolling elements is 8, and the specific parameters of bearing are shown in Table 1 [9]. When measuring, the motor speed is 1797 r/min. According to the bearing parameters and motor speed, the bearing fault characteristic frequency is calculated, as shown in Table 2. Slight damage to the rolling bearing at the fan end of the motor, and the vibration signal of the fan end was collected with a sampling frequency of 12 kHz.

Table 1Parameters of bearing SKF-6205 [9]

Inner ring diameter / mm	Outer ring diameter / mm	Thickness / mm	Ball body diameter / mm	Pitch diameter / mm
17	40	12	6.75	28.5

Table 2Fault characteristic frequency of bearing SKF-6203

Parameter	Characteristic frequency of inner ring	Characteristic frequency of outer ring	Characteristic frequency of ball body
Frequency /Hz	148.16	91.44	119.42

4.2. Experimental analysis

The uniform white noise with intensity of 0.2 is added to the inner ring, outer ring and ball body fault signals in turn, and then EEMD decomposition is performed. The screening results of each fault signal are shown in Fig. 1.

Through the correlation coefficient criterion method, the above different fault type signals decomposed by EEMD are effectively screened, and IMF components with correlation coefficient less than the threshold value of 0.1 are removed, and then reconstructed. Next, perform energy feature extraction and normalize it. Input the extracted energy fault features into the established BP neural network diagnosis system, and set the transfer functions of the hidden layer and output layer to logsig and purelin respectively, the number of training sessions is set to 1,000 and the minimum mean square error index is set at 10-8. In this paper, there are four failure modes of rolling bearings: no failure (1, 0, 0, 0), bearing inner ring failure (0, 1, 0, 0), rolling element failure (0, 0, 1, 0), bearing outer ring failure (0, 0, 0, 1).

In order to test the effectiveness of the diagnosis method proposed in this paper, the traditional wavelet packet and redundant lifting scheme packet are respectively used for denoising pre-treatment, and then the same BP neural network is used for training. The output results of the network are shown in Fig. 2 and Fig. 3, respectively. The results show that the running time of BP neural network based on redundant lifting scheme packet is 0.911250 seconds, while that of BP neural network based on traditional wavelet packet is 1.519367 seconds. Obviously, the BP neural network based on the redundant lifting scheme packet is more efficient. In addition, Table 3 shows the network input results of the two methods. It is not difficult to see that the diagnosis method proposed in this paper has higher diagnostic accuracy.

Fig. 1Bearing fault signal EEMD decomposition results

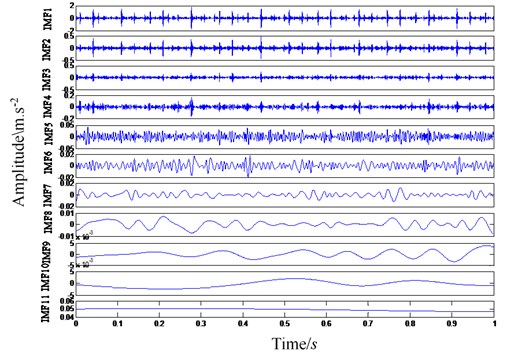
a) EEMD decomposition results of inner ring fault signal

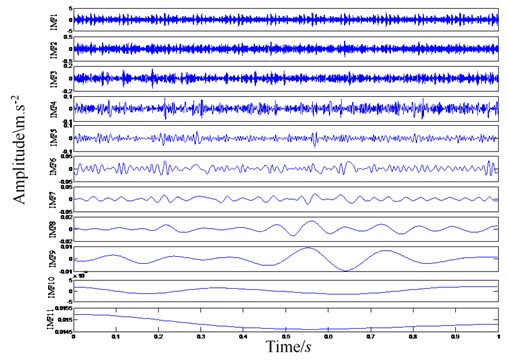
b) EEMD decomposition results of outer ring fault signal

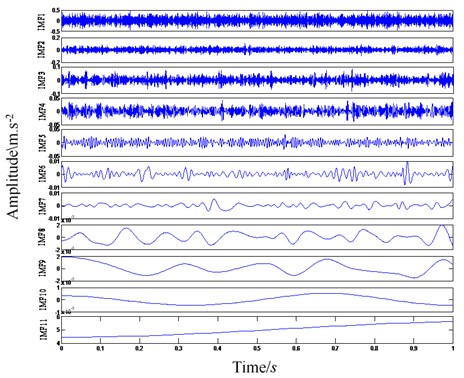
c) EEMD decomposition result of ball body failure signal

Fig. 2Output result of BP neural network based on traditional wavelet packet. Elapsed time is 1.519367 seconds

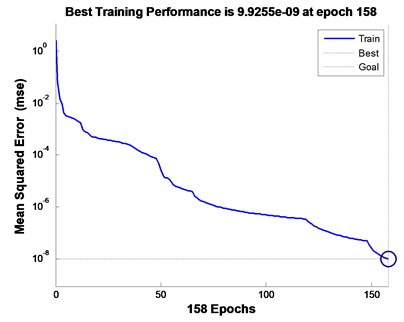
a) Number of iterations

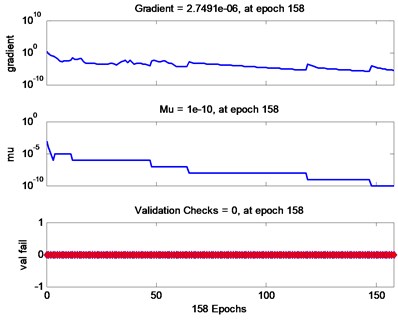
b) Training process

Fig. 3Output result of BP neural network based on traditional wavelet packet. Elapsed time is 0.911250 seconds

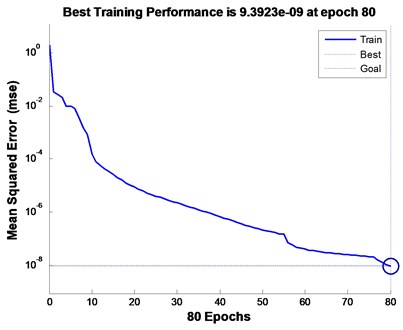
a) Number of iterations

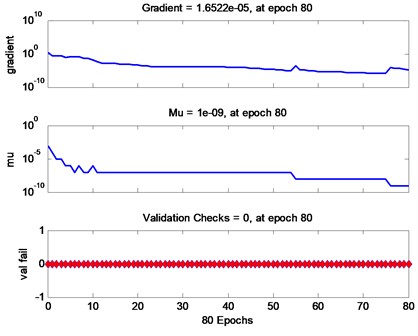
b) Training process

Table 3Network output

Pretreatment method	BP Network output				Error
Traditional wavelet packet	0.9999	0.0003	0.0002	0.0000	0.0000
	0.0001	0.9997	–0.0001	–0.0002	0.2760
	0.0001	0.3715	0.9888	0.0473	0.3381
	–0.0000	–0.3715	0.4111	0.9529	0.0044
Redundant lifting scheme packet	0.9999	-0.0003	0.0002	0.0001	0.0000
	0.0001	1.0244	–0.1708	–0.0690	0.0141
	–0.0006	0.0693	1.0506	0.0357	0.0461
	0.0006	–0.0934	0.1200	1.0333	0.0071

5. Conclusions

In order to effectively extract the vibration signal of early fault of rolling bearing which is easy to be submerged by strong noise, we propose a novel fault diagnosis method by combining EEMD and redundant lifting scheme packet. Using the new method, we first perform signal screening and denoising pretreatment, and then extract more effective fault signal. In order to realize the classification of different rolling bearing faults, the energy feature of the preprocessed fault signal is extracted and used as the input of BP neural network. The diagnosis results of BP neural network show that the proposed diagnosis method has higher diagnosis accuracy and efficiency than the traditional wavelet packet.

References

Xu G., Hou D., Qi H., et al. High-speed train wheel set bearing fault diagnosis and prognostics: A new prognostic model based on extendable useful life. Mechanical Systems and Signal Processing, Vol. 146, 2021, p. 107050.

Publisher
Chen G., Liu M., Chen J. Frequency-temporal-logic-based bearing fault diagnosis and fault interpretation using Bayesian optimization with Bayesian neural networks. Mechanical Systems and Signal Processing, Vol. 145, 2020, p. 106951.

Publisher
Xiao S., Song M., Lai L. Fault diagnosis new method of rolling bearing based on adaptive redundant lifting scheme packet. Journal of Mechanical Strength, Vol. 5, 2015, p. 816-822.

Search CrossRef
Chen J., Zhang L., Duan L., et al. Diagnosis of reciprocating compressor piston-cylinder liner wear fault based on lifting wavelet packet. Journal of China University of Petroleum: Natural Science Edition, Vol. 35, Issue 1, 2011, p. 130-134.

Search CrossRef
Helske J., et al. (R interface). Rlibeemd: Ensemble Empirical Mode Decomposition (EEMD) and Its Complete Variant (CEEMDAN). International Journal of Public Health, Vol. 60, Issue 5, 2016, p. 1-9.

Search CrossRef
Wang T., Zhang M., Yu Q., et al. Comparing the applications of EMD and EEMD on time–frequency analysis of seismic signal. Journal of Applied Geophysics, Vol. 83, 2012, p. 29-34.

Publisher
Li Y., Via B., Li Y. Lifting wavelet transform for Vis-NIR spectral data optimization to predict wood density. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, Vol. 240, 2020, p. 118566.

Publisher
Haghighi B., Taherinia A., Monsefi R. An effective semi-fragile watermarking method for image authentication based on lifting wavelet transform and feed-forward neural network. Cognitive Computation, Vol. 12, 2020, p. 863-890.

Publisher
Bearing Data Center Seeded Fault Test Data. Case Western Reserve University, http://csegroups.case.edu/bearingdatacente, 2008.

Search CrossRef

Cited by

Proceedings of IncoME-VI and TEPEN 2021

Wang Xing-he | Wang Hong-jun | Cui Ying-jie | Liu Ze-rui

(2023)

Method for Denoising the Vibration Signal of Rotating Machinery through VMD and MODWPT

(2023)

A Composite Method of Marine Shafting’s Fault Diagnosis by Ship Hull Vibrations Based on EEMD

Xiaofei Wen | Wenjie Meng | Xiaoxiao Sun | Ruiping Zhou | Liu Jing

(2022)

Improving the sensitivity of early rub detection in rotating machines with an adaptive orthogonal filter

Alejandro Silva | Carlos González-Guillén | Miguel Ruiz-García | María Elena Domínguez-Jiménez

(2022)

About this article

Received

10 October 2020

Accepted

28 October 2020

Published

05 November 2020

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/vp.2020.21733

Keywords

bearing fault

EEMD

redundant lifting scheme packet

traditional wavelet packet

Acknowledgements

This paper was supported by the following research projects: by the Natural Science Foundation of Fujian Province (Grant No. 2020J01432), Special Project of Ningde Normal University (Grant No. 2018ZX401, Grant No. 2019ZX401). These supports are gratefully acknowledged.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 10 09

Extraction and diagnosis of rolling bearing fault signals based on improved wavelet transform

Zhiqing Cheng

Research article

2019 11 15

Novel complete ensemble EMD with adaptive noise-based hybrid filtering for rolling bearing fault diagnosis

Xiaojun Song, Hongwei Sun, Liwei Zhan

Research article

2019 09 30

Bearing fault diagnosis based on feature extraction of empirical wavelet transform (EWT) and fuzzy logic system (FLS) under variable operating conditions

Fawzi Gougam, Chemseddine Rahmoune, Djamel Benazzouz, Boualem Merainani

Research article

2018 09 30

Feature extraction for rolling element bearing weak fault based on MOMEDA and ICEEMDAN

Lei Zhao, Yongxiang Zhang, Danchen Zhu

H. Su, M. Song, and Z. Xiong, “Bearing fault diagnosis method based on EEMD and adaptive redundant lifting scheme packet,” Vibroengineering PROCEDIA, Vol. 34, pp. 14–19, Nov. 2020, https://doi.org/10.21595/vp.2020.21733

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2020.21733
UR  - https://doi.org/10.21595/vp.2020.21733
TI  - Bearing fault diagnosis method based on EEMD and adaptive redundant lifting scheme packet
T2  - Vibroengineering PROCEDIA
AU  - Su, Hongtao
AU  - Song, Mengmeng
AU  - Xiong, Zicheng
PY  - 2020
DA  - 2020/11/05
PB  - JVE International Ltd.
SP  - 14-19
VL  - 34
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Su_2020,
	doi = {10.21595/vp.2020.21733},
	url = {https://doi.org/10.21595/vp.2020.21733},
	year = 2020,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {34},
	pages = {14--19},
	author = {Hongtao Su and Mengmeng Song and Zicheng Xiong},
	title = {Bearing fault diagnosis method based on {EEMD} and adaptive redundant lifting scheme packet},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]H. Su, M. Song, and Z. Xiong, “Bearing fault diagnosis method based on EEMD and adaptive redundant lifting scheme packet,” Vibroengineering PROCEDIA, vol. 34, pp. 14–19, Nov. 2020, doi: 10.21595/vp.2020.21733.

Copy IEEE

Copied to clipboard!

Su, Hongtao, Mengmeng Song, and Zicheng Xiong. “Bearing Fault Diagnosis Method Based on EEMD and Adaptive Redundant Lifting Scheme Packet.” Vibroengineering PROCEDIA 34 (November 5, 2020): 14–19. https://doi.org/10.21595/vp.2020.21733.

Copy Chicago

Copied to clipboard!

Bearing fault diagnosis method based on EEMD and adaptive redundant lifting scheme packet

Abstract

Highlights

1. Introduction

2. Brief introduction to the principle of the diagnosis plan

2.1. EEMD principle

3. Decomposition and reconstruction algorithm of adaptive redundant lifting scheme packet

4. Experimental results and analysis

4.1. Experimental setup

4.2. Experimental analysis

5. Conclusions

References

Cited by

About this article

Related Articles