Bearing fault feature extraction method based on complete ensemble empirical mode decomposition with adaptive noise

Xiao, Maohua; Zhang, Cunyi; Wen, Kai; Xiong, Longfei; Geng, Guosheng; Wu, Dan

doi:10.21595/jve.2018.19562

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 November 2018

Check for updates

Bearing fault feature extraction method based on complete ensemble empirical mode decomposition with adaptive noise

Maohua Xiao¹

Cunyi Zhang²

Kai Wen³

Longfei Xiong⁴

Guosheng Geng⁵

Dan Wu⁶

^{1, 2, 3, 4, 5, 6}College of Engineering, Nanjing Agricultural University, Nanjing, 210031, China

Corresponding Author:

Maohua Xiao

Cite the article Download PDF

Downloads 1499

WoS Core Citations 8

CrossRef Citations 8

Abstract

As an important part of rotating machinery, bearings play an important role in large-scale mechanical equipment. Abnormal bearing conditions may cause the machine to malfunction, or even evolve into a serious accident. Therefore, the accurate and timely fault diagnosis of the bearing is of great significance. Based on EMD, this paper introduces the working principles and characteristics of EEMD and CEEMDAN, respectively. Then the signal was decomposed by EEMD and CEEMDAN respectively. The simulation results show that CEEMDAN has better effect on signal decomposition. Then, comparing the effect of CEEMDAN and EEMD on bearing fault feature frequency extraction, the experiment proves that CEEMDAN has a better ability to preserve original signal and eliminate noise than EEMD method, and can extract bearing fault feature more accurately and timely.

1. Introduction

As an important part of rotating machinery, bearings play an important role in large-scale mechanical equipment. However, due to the harsh working environment of the bearing, including corrosion, poor lubrication and plastic deformation, the bearing becomes one of the most easily broken parts of the machine. In order to diagnose bearing failures in a timely manner and prevent unpredictable accidents, it is particularly important to study bearing fault feature extraction techniques. In engineering applications, the fault characteristic frequency of the bearing is often extracted from the collected vibration signal. Therefore, vibration signal processing technology is widely used in the industrial field as the main analysis technology for bearing fault diagnosis.

EMD is a new time-frequency analysis method proposed by Huang, which can decompose the signal into several intrinsic modal functions (IMFs) [1, 2]. The method can perform adaptive selection of base at the same time when multi-resolution decomposition is completed. This method solves the problem of base selection and is suitable for handling nonlinear and non-stationary signals. However, mode mixing may occur when decomposing the intrinsic mode component (IMC) [3, 4]. In order to reduce the mode mixing, Wu Z. et al. proposed the Ensemble Empirical Mode Decomposition (EEMD), which reduces the effect of mode mixing by adding auxiliary white noise and achieves good results to a certain extent [5, 6]. Zheng J. et al. proposed a partly ensemble EMD (PEEMD) method to solve the problem of mode mixing, which is an improvement on EEMD [7]. However, EEDM also has the problems of low decomposition efficiency, too many pseudo-components, and ineffective extraction of fault features.

In order to solve these problems of the EEMD, Torres M. E. et al. proposed the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) method with adaptive noise [8]. This method adds adaptive white noise in each decomposition stage to reduce the mode mixing. Colominas M. A. et al. used the IMF of Gaussian white noise decomposed by EMD as the unique noise to be added at each decomposition stage to solve the “false” IMFs that may be generated after CEEMDAN decomposes the signal [9]. Lei Y. et al. also applied this method to the fault diagnosis of locomotive rolling bearings [10]. But the diagnostic efficiency of this method was greatly reduced. This paper describes the use of CEEMDAN in bearing feature extraction and uses experiments to compare the accuracy of the proposed method with EEMD, and verifies the feasibility of the proposed method [11, 12].

The rest of this study is organized as follows. Section 2 presents the basic principles of EEMD and CEEMDAN. Section 3 describes and compares the simulation of EEMD and CEEMDAN. Section 4 provides an empirical comparison of the feature extraction between EEMD and CEEMDAN. Section 5 presents a concluding summary.

2. Basic principles of EEMD and CEEMDAN

2.1. EEMD’s principles

EMD is based on the time scale characteristics of complex signal itself without any requirement to setup any basis functions [13]. This method decomposes noise signals into a series of data sequence retaining local feature information, which is called Intrinsic Mode Function (IMF). Based on this characteristic, EMD has a high signal-to-noise ratio while dealing with non-stationary and nonlinear data. EMD method needs to meet the following 3 conditions:

(1) At least one maxima and one minimum must be contained in the signal.

(2) Time characteristic scale is defined by the time interval between adjacent extreme points.

(3) If there is no extreme point in the whole signal, but a turning point is available. Then differential can be done to the signal to obtain the extreme points. Finally, obtain the final decomposition results through the integration of IMFs.

The EEMD method is improved on the basis of the EMD method. The mode mixing phenomenon will frequently appear while using EMD method. The reasons are as the following due to two kinds of circumstances:

(1) A separate IMF signal contains completely different scale.

(2) The same scale appears in different IMFs. The EEMD method used the statistic characteristic that white Gaussian noise has a uniform frequency distribution. After additional Gauss white noise background is added in the signal, signal region at different scales will be automatically mapped to the appropriate scale of background white noise. This makes it possible to have a unified framework for the analysis of time scales which can separate various time scales clearly, enhance the anti-mixing effect and form an effective, adaptive, and dynamic two filter group, solving the mode mixing problem of EMD method.

The specific process of EEMD method:

(1) Add Gauss white noise with zero mean and variance as constant $ω (t)$ on the original signal $γ (t)$ and get a new target signal $Y (t)$ :

1

Υ (t) = γ (t) + ω (t) .

(2) Imply EMD decomposition on the signal $Y (t)$ . Obtained A series of IMF components and residual components $r_{Ν} (t)$ of the target signal:

2

Υ (t) = \sum_{j = 1}^{N} i m f_{j} (t) + r_{N} (t) .

(3) Add $N$ sub different white noise to the target signal, and repeat the steps above:

3

Υ_{i} (t) = \sum_{j = 1}^{N} i m f_{i j} (t) + r_{i N} (t) .

(4) Do overall average operation of the above results to eliminate the influence of the many times adding of Gauss white noise on real IMF. Get the IMF component:

4

i m f_{j} (t) = \frac{1}{n} \sum_{i = 1}^{n} i m f_{i j} (t) .

2.2. CEEMDAN’s principle

EEMD has great significance in solving the problem of mode mixing in EMD. But it has several drawbacks. First, a large amount of computation is needed. Second, many false components will be decomposed and achieved if the parameter chosen is not reasonable. Torres M E and others put forward CEEMDAN method to solve this problem. This method adds adaptive white noise in every decomposing stage and calculates the only left residual signal to achieve every model component [14]. In this way, the problem of EEMD was solved.

The specific process of CEEMDAN method:

(1) Defined operator $Ε_{k} (∙)$ to represents the first $k$ modal component generated by the EMD calculation. $ω (t)$ meet the Gauss white noise of $N$ (0, 1). $\bar{{I M F}_{k}}$ is denoted as the first $k$ modal component of the CEEMDAN algorithm. Let $Y [t]$ be the signal to be processed. CEEMDAN decomposed the signals $Y [t] + E_{0} ω_{i} (t)$ , using EMD, for $I$ times, and obtained:

5

{\bar{I M F}}_{1} = \frac{1}{I} \sum_{i = 1}^{I} {\bar{I M F}}_{i 1} .

(2) Calculate the first margin of the first phase of the ( $k =$ 1):

6

Υ_{1} [t] = Y [t] - {\bar{I M F}}_{1} .

(3) Discompose these signals $Υ_{1} [t] + ε_{1} Ε_{1} (ω_{i} [t])$ ( $i =$ 1, 2, …, $I)$ , till the first EMD mode component is decomposed. Then defined the second modal component as:

7

{\bar{I M F}}_{2} = \frac{1}{I} \sum_{i = 1}^{I} E_{1} (Υ_{1} [t] + ε_{1} E_{1} (ω_{i} [t])) .

(4) While $k =$ 2, …, $K$ , calculate the first $K$ margin:

8

Υ_{k} [t] = Υ_{k - 1} [t] - {\bar{I M F}}_{k} .

(5) Discompose these signals $Υ_{k} [t] + ε_{k} Ε_{k} (ω_{i} [t])$ ( $i =$ 1, 2, …, $I$ ), till the first EMD mode component is decomposed. Then defined the $K +$ 1 modal components as:

9

{\bar{I M F}}_{k + 1} = \frac{1}{I} \sum_{i = 1}^{I} E_{1} (Υ_{k} [t] + ε_{k} E_{k} (ω_{i} [t])) .

(6) Add 1 to $K$ , continue to carry out step 4 till the residual signal achieved can’t be decomposed any more (every residual signal contains on more than one extreme point). Finally, $K$ intrinsic mode functions are obtained. Residual signals meet:

10

\bar{R [t]} = Y [t] - \sum_{k = 1}^{K} {\bar{I M F}}_{k} .

3. Simulation

Harmonics are resonant waves with the same frequency or multiple frequencies as the main wave! They are parasitized with the main wave! It is commonly known as harmonics and higher harmonics! In order to verify CEEMDAN’s better denoising effect, this paper strictly set the same harmonic signals: 50 Hz, 150 Hz, and 300 Hz for simulation experiments. To better compare the decomposition performance of CEEMDAN and EEMD on the signal, set the same input parameters for the two methods, that is, the white noise amplitude is 0.1, the ensemble size is 100, and the sampling frequency is 2000 Hz, to ensure that the simulation verification is more accurate. The sampling time is 2 s and $i (t)$ is the gause white noise signal, as shown in Eq. (11):

11

x (t) = 2 \sin (100 π t) + 3 \cos (300 π t) + \sin (600 π t) + i (t) .

The modal components are obtained by the decomposition of signals. However, some pseudo modal components are often obtained and not associated with original signals. So, these pseudo modal components in modal components need to be identified and eliminated. Calculate the correlation coefficient between each modal component and the original signal and remove the pseudo modal component. The formula of the correlation coefficient is following:

12

r_{X Y} = \frac{\sum_{i = 1}^{N} (X_{i} - \bar{X}) (Y_{i} - \bar{Y})}{\sqrt{\sum_{i = 1}^{N} {(X_{i} - \bar{X})}^{2}} \sqrt{\sum_{i = 1}^{N} {(Y_{i} - \bar{Y})}^{2}}} .

Fig. 1 shows the correlation coefficients between the first 8 modes of EEMD decomposition and the original signal. Obviously, the correlation coefficient of the first four modes is much larger than that of other modes. So, extract the first four modal components and reconstruct them. This eliminates residual modal components in the signal.

Fig. 1The correlation coefficient between the first 8 modes decomposed by EEMD and original signal

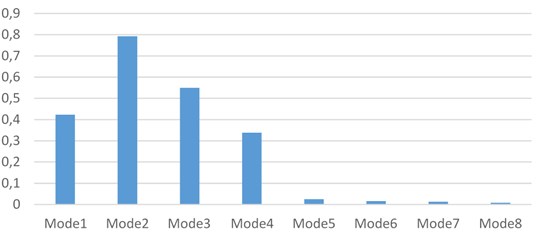
Fig. 2The correlation coefficient between the first 8 modes decomposed by CEEMDAN and original signal

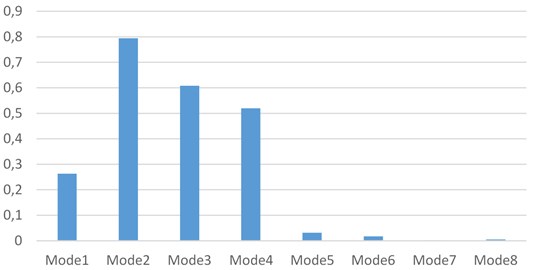
Fig. 2 shows the correlation coefficients between the first 8 modes of the CEEMDAN decomposition and the original signal. In the same way, the first four modal components are extracted and reconstructed to eliminate residual modal components in the signal.

The signals were decomposed using EEMD and CEEMDAN, respectively. Then calculate the correlation coefficient between the reconstructed signal and the original signal. The signal-noise ratio reflects the purity of the signal, the larger the SNR, the stronger the signal purity. The signal-to-noise ratio of the reconstructed signal is calculated by the following equation:

13

S_{N R} = 10 \times \log_{10} \{\sum_{i = 1}^{N} \frac{{S_{i}}^{2}}{\sum_{i = 1}^{N} {(S_{i} - {S_{i}}^{'})}^{2}}\} .

Table 1 shows the correlation coefficient between the original signal and the reconstructed signal processed by the two methods, and also shows the signal-to-noise ratio of the reconstructed signal processed by the two methods.

Table 1The correlation coefficient and signal-to-noise ratio

	Processed by EEMD	Processed by CEEMDAN
Correlation coefficient	0.9769	0.9774
Signal to noise ratio	13.1768	13.2108

Table 1 shows the correlation coefficient between the original signal and the reconstructed signal processed by the two methods.

From Table 1, it can be concluded that the proposed method can effectively remove the interference factors in the signal and the resulting reconstructed signal can better reflect the original signal.

4. Feature extraction

To verify the effectiveness of this method, this paper chooses the rolling bearing as the research object then process the vibration signal of the bearing outer ring and the inner ring fault respectively.

Bearing outer ring fault characteristic frequency expression is:

14

f_{o} = \frac{1}{2} (1 - \frac{d}{D_{m}} c o s α) f_{n} Z .

Bearing inner ring fault characteristic frequency expression is:

15

f_{i} = \frac{1}{2} (1 + \frac{d}{D_{m}} c o s α) f_{n} Z .

In the equation, $Ζ$ represents the number of rolling elements, d presents the diameter of rolling body, a represents the bearing contact angle, $D_{m}$ represents the pitch circle diameter of bearing and $f_{n}$ presents rotating frequency.

This paper uses bearing data measured by fault simulation test platform of rolling bearing in Electrical Engineering Laboratory of Case Western Reserve University.

The platform’s parameters are set as follows:

Bearing type is 6205-2RS JEM SKF, bearing speed is 1797 r/min, the sampling frequency is 12 kHz, the number of data points is 4096, and fault diameter set is 0.021 inches. Measuring points are arranged in the drive motor output of the platform.

The following Table 2 shows the fault frequency of the bearing outer ring and the inner ring calculated by the Eq. (14) and the Eq. (15).

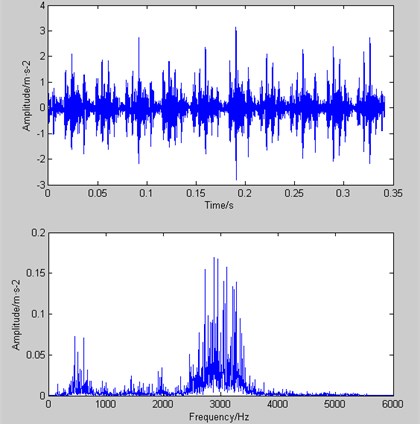
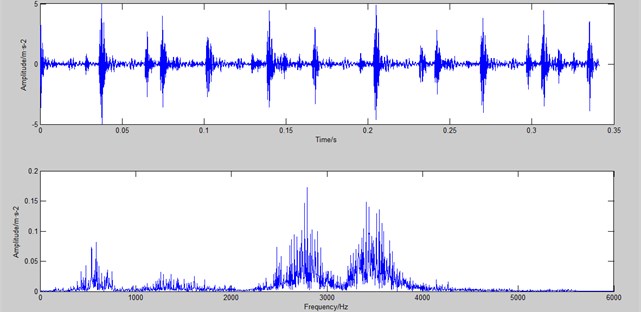
In Fig. 3, the time domain waveform and spectrum of the fault signal of the inner ring are presented, when the bearing’s rotational speed is at 1797 rpm. And from Fig. 3, it is appreciated that the spectrum cannot identify directly the fault frequency mixed with a variety of noise signals.

Table 2Bearing fault characteristic frequency

Rotational frequency $f_{n}$	Outer ring fault frequency $f_{0}$	Inner fault frequency $f_{i}$
29.95 Hz	107.36 Hz	162.18 Hz

Fig. 3The time domain waveform and spectrum of the fault signal of the inner ring at 1797 rpm

In the case of decomposing the inner ring’s fault signal through EEMD and CEEMDAN separately, the total modal number of CEEMDAN, both are 12, doesn’t have any increase compared with EEMD. Usually, the several modes in front, produced by extraction, are chosen as research objects because their correlation coefficients with original signals are high. Therefore, the paper takes the first 4 modes of EEMD and CEEMDAN respectively as the research objects. Which are shown in Fig. 4 and Fig. 5.

Fig. 4The first 4 modes of EEMD (the inner ring)

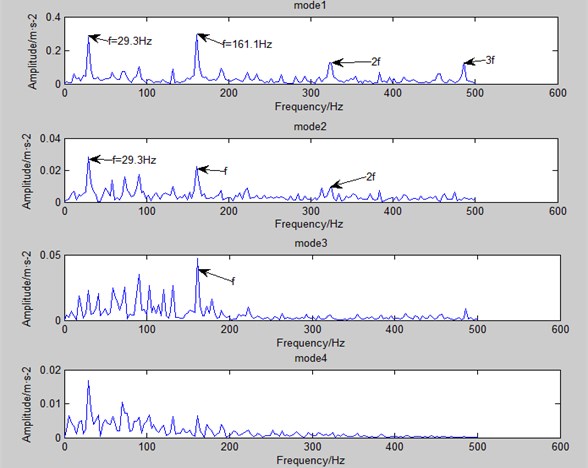
Fig. 5The first 4 modes of CEEMDAN (the inner ring)

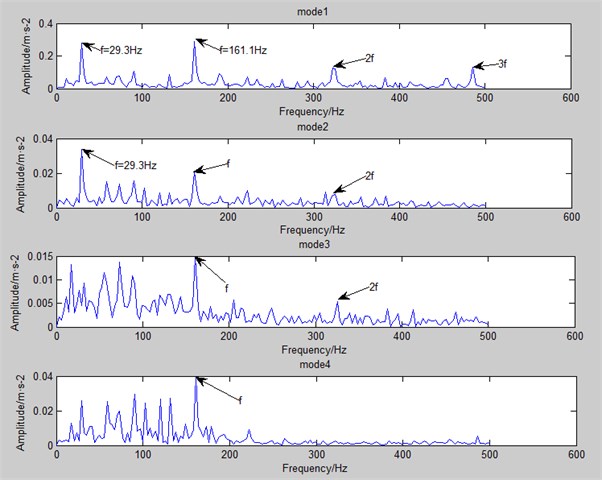
In Fig. 4 and Fig. 5, the frequency around 29.5 Hz is bearing rotational frequency, and that around 162 Hz is of inner ring fault. What’s more, 2 $f$ frequency can also be seen in the figure, which is equal to 2 times the fault frequency, and 3 $f$ etc. it can be found obviously that CEEMDAN can find out more fault frequency and multiple frequency (especially in mode 3 and mode 4).

In addition, the paper uses the decomposed spectrum to analyse the case of outer ring. In Fig. 6, the time domain waveform and spectrum of the fault signal of the outer ring are presented, when the bearing's rotational speed is at 1797 rpm. As it can be seen, the fault frequency mixed with a variety of noise signals cannot be identified directly.

Fig. 6The time domain waveform and spectrum of the fault signal of the outer ring at 1797 rpm

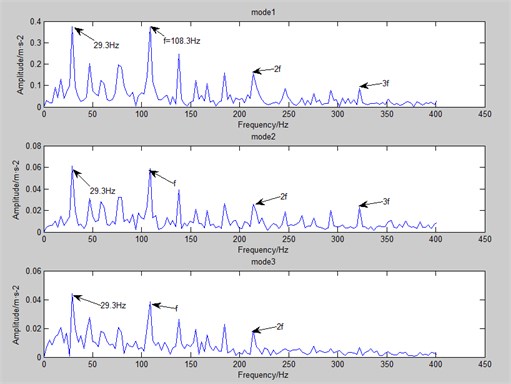
As is shown in Fig. 7 and Fig. 8, EEMD and CEEMDAN is applied to decompose the outer ring fault signal separately. EEMD produces 12 modes, and CEEMDAN produces 13 modes. The total modal number of CEEMDAN is only 8 % more than EEMD and there isn’t any obvious increase. Just like the case in inner ring’s spectrum. The several modes in front have higher correlation coefficient with original signals. Therefore, the paper takes the first 3 modes of CEEMDAN and EEMD respectively as the research objects.

In spectrum above, the frequency around 29.5 Hz is bearing rotational frequency, and that around 108 Hz is of outer ring fault. What’s more, it can be seen 2 $f$ frequency, 3 $f$ frequency etc. It is easy to find that CEEMDAN can find out more fault frequency and multiple frequency (especially in mode 3).

In conclusion, CEEMDAN is more effective than EEMD in extracting the characteristic frequencies of the fault signals inside and outside the bearing. Multiple modal components processed by CEEMDAN can identify the failure frequency of the signal. However, signals processed by EEMD are prone to mode mixing.

Fig. 7The first 3 modes of EEMD (the outer ring)

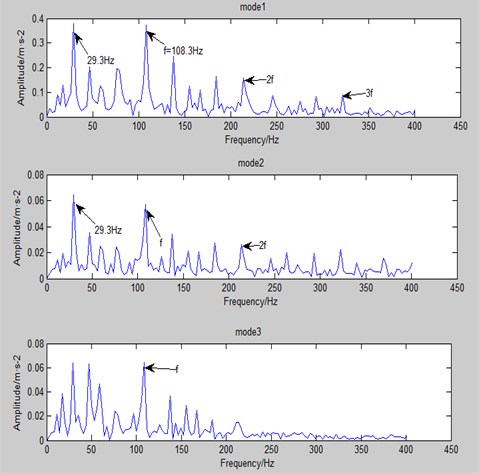
Fig. 8The first 3 modes of CEEMDAN (the outer ring)

5. Conclusions

Based on the EMD, this paper describes in detail the working principles and features of EEMD and CEEMDAN. The feature extraction method in bearing fault diagnosis was analyzed. Through simulation experiments and bearing fault feature extraction experiments, this paper verifies that CEEMDAN has great advantages in retaining original signal information and eliminating signal noise. As a new technology to study bearing fault feature extraction, CEEMDAN has important research value and application prospects.

References

Huang N., Shen Z., Long S., Wu M., Shih H., Zheng Q., Yen N., Tung C., Liu H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of The Royal Society A, Vol. 454, 1998, p. 903-995.

Publisher
Hao F., Xu G., Huang X. Explosive NQR signal processing based on empirical mode decomposition and wavelet transform. Vibration and Shock, Vol. 16, 2014, p. 183-187.

Search CrossRef
Liu Z., Sun W., Zeng J. A new short-term load forecasting method of power system based on EEMD and SS-PSO. Neural Computing and Applications, Vol. 24, Issues 3-4, 2014, p. 973-983.

Publisher
Singh D. S., Zhao Q. Pseudo-fault signal assisted EMD for fault detection and isolation in rotating machines. Mechanical Systems and Signal Processing, Vol. 81, 2016, p. 202-218.

Publisher
Wu Z., Huang N. E. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, 2009, https://doi.org/10.1142/S1793536909000047.

Publisher
Wu Z., Huang N. E., Chen X. The multi-dimensional ensemble empirical mode decomposition method. Advances in Adaptive Data Analysis, Vol. 1, Issue 3, 2009, p. 339-372.

Publisher
Zheng J., Cheng J., Yang Y. Partly ensemble empirical mode decomposition: an improved noise-assisted method for eliminating mode mixing. Signal Processing, Vol. 96, 2014, p. 362-374.

Publisher
Torres M. E., Colominas M. A., Schlotthauer G., et al. A complete ensemble empirical mode decomposition with adaptive noise. IEEE International Conference on Acoustics, Speech and Signal Processing, 2011, p. 4144-4147.

Publisher
Colominas M. A., Schlotthauer G., Torres M. E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomedical Signal Processing and Control, Vol. 14, 2014, p. 19-29.

Publisher
Lei Y., Liu Z., Ouazri J., et al. A fault diagnosis method of rolling element bearings based on CEEMDAN. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 231, Issue 10, 2017, p. 1804-1815.

Publisher
Xu X., Jiang Y., Pueh L. Multi-objective optimal design of sandwich panels using a genetic algorithm. Engineering Optimization, Vol. 49, Issue 10, 2017, p. 1665-1684.

Publisher
Xu X., Jiang Y., Pueh L., Chen N. Sound insulation performance optimization of lightweight sandwich panels. Journal of Vibroengineering, Vol. 18, Issue 4, 2016, p. 2574-2586.

Publisher
Satish M., Karunesh K., Kota S. Vibro-acoustic fault analysis of bearing using FFT, EMD, EEMD and CEEMDAN and their implications. Advances in Machine Learning and Signal Processing, Vol. 387, 2016, p. 281-292.

Publisher
Bouhalais M., Djebala A., Ouelaa N., et al. CEEMDAN and OWMRA as a hybrid method for rolling bearing fault diagnosis under variable speed. International Journal of Advanced Manufacturing Technology, Vol. 94, Issues 5-8, 2018, p. 2475-2489.

Publisher

Cited by

Intelligent Cavitation Recognition of a Canned Motor Pump Based on a CEEMDAN-KPCA and PSO-SVM Method

Xiaojun Li | Haitao Yang | Jie Ge | Shuai Zhu | Zuchao Zhu

(2024)

Study on the Effect of Oil Supply on the Sound Field Characteristics of Full Ceramic Ball Bearings under Oil Lubrication

(2023)

A new adaptive WVS based denoising method on GNSS vertical time series

Zhengkai Huang

(2023)

Multi-scale and multi-layer perceptron hybrid method for bearings fault diagnosis

Suchao Xie | Yaxin Li | Hongchuang Tan | Runda Liu | Fengyi Zhang

(2022)

Automatic Transmission Bearing Fault Diagnosis Based on Comprehensive Index Method and Convolutional Neural Network

Guangxin Li | Yong Chen | Wenqing Wang | Yimin Wu | Rui Liu

(2022)

Transient Fault Detection and Location in Power Distribution Network: A Review of Current Practices and Challenges in Malaysia

Saidatul Habsah Asman | Nur Fadilah Ab Aziz | Ungku Anisa Ungku Amirulddin | Mohd Zainal Abidin Ab Kadir

(2021)

Improved Butterfly Optimizer‐Configured Extreme Learning Machine for Fault Diagnosis

(2021)

2020 IEEE 16th International Conference on Control & Automation (ICCA)

Zhenjin Shi | Yueyang Li | Shuai Liu

(2020)

About this article

Received

22 December 2017

Accepted

15 June 2018

Published

15 November 2018

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2018.19562

Keywords

CEEMDAN

EEMD

denoising

fault diagnosis

feature extraction

bearings

Acknowledgements

The research is funded partially by the National Key Research and Development Program of China (2016YFD0701103) and the China Postdoctoral Science Foundation (2016M601800).

Author Contributions

Maohua Xiao contributed to the design and optimization of the algorithm. Cunyi Zhang, Kai Wen·and Longfei Xiong performed the processing and analysis of experimental data and the completion of the manuscript. Guosheng Geng and Da Wu performed the revision of the manuscript.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 11 24

Fault diagnosis of bearing vibration signals based on a reconstruction algorithm with multiple side Information and CEEMDAN method

Bo Wu, Yangde Gao, Na Ma, Theerasak Chanwimalueang, Xiaobing Yuan, Jianpo Liu

Research article

2019 11 15

Novel complete ensemble EMD with adaptive noise-based hybrid filtering for rolling bearing fault diagnosis

Xiaojun Song, Hongwei Sun, Liwei Zhan

Research article

2018 09 30

Feature extraction for rolling element bearing weak fault based on MOMEDA and ICEEMDAN

Lei Zhao, Yongxiang Zhang, Danchen Zhu

Research article

2018 02 15

Rolling bearing fault diagnosis based on improved complete ensemble empirical mode of decomposition with adaptive noise combined with minimum entropy deconvolution

Abdelkader Rabah, Kaddour Abdelhafid

M. Xiao, C. Zhang, K. Wen, L. Xiong, G. Geng, and D. Wu, “Bearing fault feature extraction method based on complete ensemble empirical mode decomposition with adaptive noise,” Journal of Vibroengineering, Vol. 20, No. 7, pp. 2622–2631, Nov. 2018, https://doi.org/10.21595/jve.2018.19562

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2018.19562
UR  - https://doi.org/10.21595/jve.2018.19562
TI  - Bearing fault feature extraction method based on complete ensemble empirical mode decomposition with adaptive noise
T2  - Journal of Vibroengineering
AU  - Xiao, Maohua
AU  - Zhang, Cunyi
AU  - Wen, Kai
AU  - Xiong, Longfei
AU  - Geng, Guosheng
AU  - Wu, Dan
PY  - 2018
DA  - 2018/11/15
PB  - JVE International Ltd.
SP  - 2622-2631
IS  - 7
VL  - 20
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Xiao_2018,
	doi = {10.21595/jve.2018.19562},
	url = {https://doi.org/10.21595/jve.2018.19562},
	year = 2018,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {20},
	number = {7},
	pages = {2622--2631},
	author = {Maohua Xiao and Cunyi Zhang and Kai Wen and Longfei Xiong and Guosheng Geng and Dan Wu},
	title = {Bearing fault feature extraction method based on complete ensemble empirical mode decomposition with adaptive noise},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]M. Xiao, C. Zhang, K. Wen, L. Xiong, G. Geng, and D. Wu, “Bearing fault feature extraction method based on complete ensemble empirical mode decomposition with adaptive noise,” Journal of Vibroengineering, vol. 20, no. 7, pp. 2622–2631, Nov. 2018, doi: 10.21595/jve.2018.19562.

Copy IEEE

Copied to clipboard!

Xiao, Maohua, Cunyi Zhang, Kai Wen, Longfei Xiong, Guosheng Geng, and Dan Wu. “Bearing Fault Feature Extraction Method Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise.” Journal of Vibroengineering 20, no. 7 (November 15, 2018): 2622–31. https://doi.org/10.21595/jve.2018.19562.

Copy Chicago

Copied to clipboard!

Bearing fault feature extraction method based on complete ensemble empirical mode decomposition with adaptive noise

Abstract

1. Introduction

2. Basic principles of EEMD and CEEMDAN

2.1. EEMD’s principles

2.2. CEEMDAN’s principle

3. Simulation

4. Feature extraction

5. Conclusions

References

Cited by

About this article

Related Articles