Abstract
There are always the nonlinear and non-stationary characteristics and periodic pulse in vibration signals of rolling element bearings when there are partial faults in those bearings. Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN) overcomes the presence of spurious modes and residual noise in Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN), but it cannot clearly and accurately extract the weak fault feature of rolling element bearings under the strong background noise. Here, Multipoint Optimal Minimum Entropy Deconvolution Adjusted (MOMEDA) was proposed. A bearing simulator was used to collect vibration signals of bearing inner and outer race, which was enhanced by MOMEDA, decomposed into several Intrinsic Mode Functions(IMFs) by ICEEMDAN, and analyzed by the envelope demodulation, finally gaining the frequency of shaft speed, BPFI (ball pass frequency, inner race) and harmonics, sidebands spaced, BPFO (ball pass frequency, outer race) and harmonics. The results show that this method can be used to accurately extract different frequency components of bearing fault vibration signals and diagnose bearing different fault location.
1. Introduction
Rolling element bearings are one of the most common components that are widely used in rotating machinery, and their failure is one of the most frequent reasons for machine breakdown. There are always the nonlinear and non-stationary characteristics and periodic pulse in vibration signals of rolling element bearings when there are partial faults in those bearings. But this faulty pulse has a large period, a low energy proportion and it is susceptible to the background noise. It is difficult to extract the fault characteristic frequency and to diagnose the bearing fault location effectively. Moreover, the traditional signal analysis technology is difficult to achieve good results. Therefore, the fault feature extraction of bearings based on multiplex methods has become a hot spot of research.
Empirical mode decomposition (EMD) is an adaptive approach to the decomposition of nonlinear and non-stationary signal presented originally by Huang et al. [1] and has been widely applied to bearing failures detection [2-4]. However, there are still some problems to be studied, such as mode-mixing and boundary effect. A novel signal processing method, called ensemble EMD (EEMD), was proposed by Wu and Huang [5] in 2009 on the basis of EMD. In order to solve mode-mixing problem of EMD, EEMD based on assistant Gaussian white noise remains the continuity under different scale [6]. Because the reconstructed signal includes residual noise, it increases the reconstruction error and reduces the completeness of signal decomposition significantly. In order to overcome it, Torres et al [7] proposed CEEMDAN. An adaptive noise is added at each stage of the decomposition and a unique residue is computed to obtain each mode. As an adaptive signal processing method, it remains the completeness of EMD, overcomes mode-mixing phenomenon of EMD and suppresses the reconstruction error [8]. But it still has two drawbacks: the existence of spurious modes and the presence of residual noise in the modes. Taking these into account, Colominas et al. [9] proposed a new algorithm called Improved CEEMDAN (ICEEMDAN), which calculates the local means of original signal to obtain each mode. Not only can the noise in the modes be reduced, but also the spurious modes caused by overlap of components can be decreased.
However, as a practical matter, the fault feature is weak in the early fault period of bearings, and susceptible to random noise. The periodic pulse is often buried in the background noise, and is not easy to identify and extract. In order to enhance the periodic impact component in the vibration signal of bearing fault, and reduce the noise interference, MOMEDA was proposed [10]. As a non-iterative deconvolution approach, MOMEDA settles a deconvolution problem by an infinite impulse train as the goal and the optimal filter solution can be given directly.
2. The Principle of the MOMEDA
Given a simple bearing vibration signal:
where is the measured bearing vibration, is transmission path, is an impulse signal, and is the white noise. Due to the influence of external context and transmission path, is attenuated to and loses the properties of original signal. It makes the frequency components complex and the energy distribution odd, which increases the entropy. The objective of the deconvolution is to find the inverse filter , which recovers the properties of signal :
Given definition of the Multi Kurtosis-Norm (MKN):
Select the corresponding to the maximum MKN:
where the target vector, , is a constant vector that defines the location and weightings of the goal impulses to be deconvolved. is filter coefficients, . is a filter length.
The above optimization problem is equivalent to solving the equation:
Given :
Since , and assuming exists:
Or in matrix form:
On account of space limitations, no specific deduction is given. Please refer to reference [10,11] for details.
3. ICEEMDAN
3.1. The principle of the ICEEMDAN
ICEEMDAN algorithm can be described as follows:
Step 1. Calculate by EMD the local means of realizations to obtain the first residue:
where is a realization of white Gaussian noise with zero mean and unit variance, is a selection of the signal-to-noise ratio (SNR).
Calculate the first mode:
Step 2. Calculate the second residue:
where is the second mode by EMD.
Then define :
Step 3. For 3, …, calculate the th residue:
Then define :
Step 4. Continue to sift until the obtained residue cannot be further decomposed (residue has less than three local extremes):
where is the final residue, is the total number of . Therefore, the signal of can be expressed as:
3.2. Comparison analysis of simulation signals
In order to demonstrate the advantages of ICEEMDAN, The EMD, EEMD, CEEMDAN, and ICEEMDAN are compared by simulation signal. The simulation signal in Fig. 1 contains a simple harmonic wave of 25 Hz, and a 110 Hz wavelet that is overlain at 0.4 s to 0.6 s. The simulation signal is decomposed by EMD, EEMD, CEEMDAN and ICEEMDAN respectively.
Fig. 2 is the result of EMD. It can be seen from the diagram that there exists mode mixing in EMD. The high frequency component is not sifted alone in IMF1, which contains low frequency component. Similarly, there is different mode-mixing in other IMFs. This complicates signal analysis and makes it difficult to identify the exact components of each IMF.
Fig. 1The waveform of simulated signal
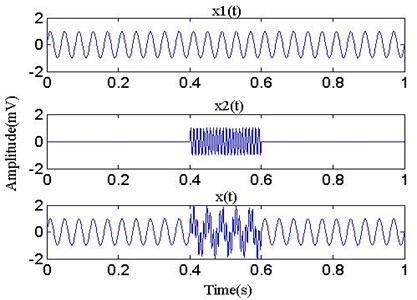
Fig. 2The waveform of EMD
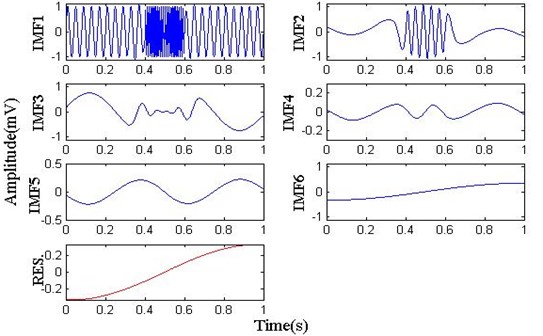
Fig. 3 is the result of EEMD with standard deviation 0.1 of the added Gauss white noise. As can be seen from the diagram, the high frequency wavelets of 110 Hz between 0.4 s and 0.6 s are fully recovered in IMF1, but there is different mode-mixing in other IMFs.
Fig. 4 is the result of CEEMD, where its parameters are the same as EEMD. It is observed from Fig. 4 that the IMF1 is similar to EEMD’s, IMF2 and IMF3 are mixed up with the residual noise and compared with EMD(IMF3-IMF6) and EEMD(IMF4-IMF9), the spurious mode appears in CEEMDAN (IMF6-IMF11), which has nothing to do with the original signal.
Fig. 3The waveform of EEMD
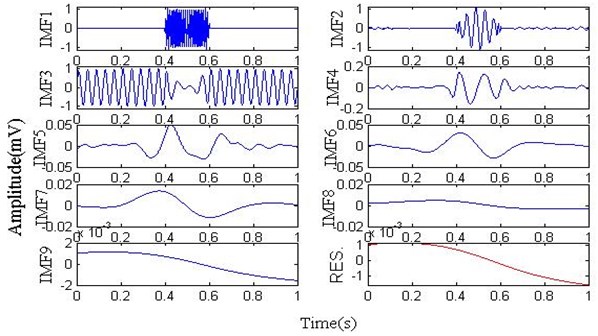
Fig. 4The waveform of CEEMDAN
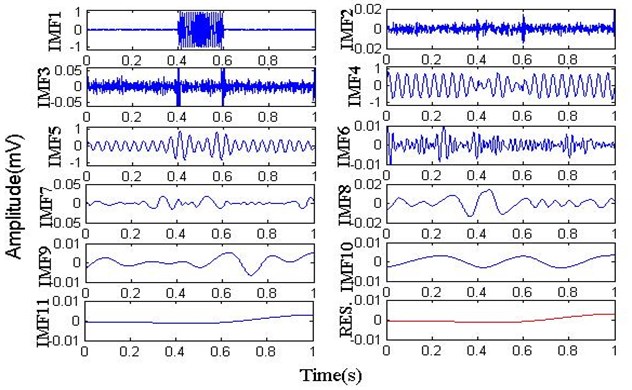
Fig. 5 is the result of ICEEMD, which is set with the same parameters as above. As can be seen from the graph, the high frequency component 110 Hz between 0.4 s and 0.6 s are fully recovered in IMF1; a simple harmonic wave 25 Hz is extracted in IMF2. The two signal components in the simulation signal are recovered, and there are no spurious modes. In conclusion, compared with EMD, EEMD and CEEMDAN, ICEEMDAN has obvious advantages in suppressing mode mixing, spurious mode, and mixing residual noise in modes.
4. Bearing fault simulation signals
In order to verify the validity of the method combining MOMEDA with ICEEMDAN, a simple fault model is used to simulate the periodic impact signal produced by the bearing fault, and the white noise is added to simulate the early fault signal of the bearing [12]:
where 3000 Hz is carrier frequency, 5 is displacement constant, 0.1 is damping coefficient, 0.01 s is the period of impact fault, 20 kHz is the sampling frequency, 4096 is the sampling number, is the sampling time, and is white noise.
Fig. 5The waveform of ICEEMDAN
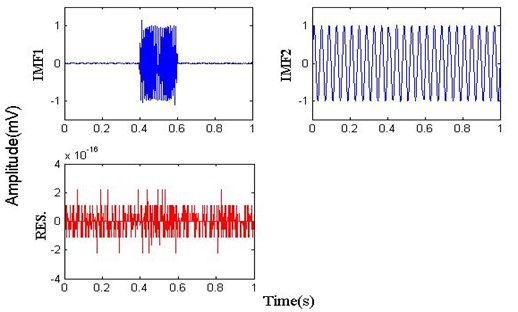
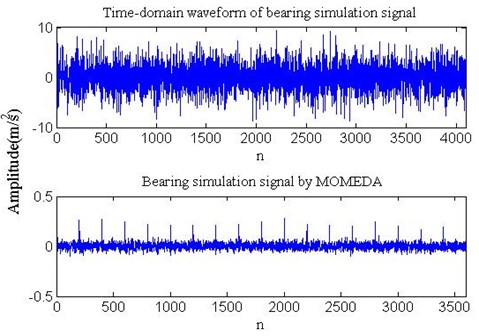
Fig. 6 is the time-domain waveform of bearing simulation signal and by MOMEDA. Because the bearing fault impact signal is affected by noise, it is unable to recognize the fault information. The bearing simulation signal is processed by MOMEDA, and its kurtosis has a sharp rise, which increases from 3.15 to 12.87. What’s more, the impact signal in the time-domain waveform is more obvious.
Fig. 6Time-domain waveform of bearing simulation signal
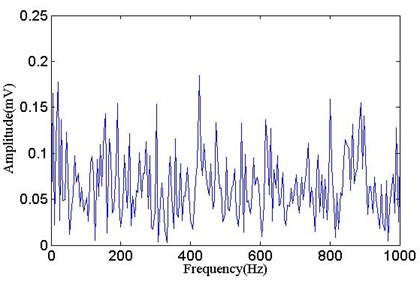
The signal after MOMEDA is decomposed into several IMFs by ICEEMDAN, and then the first IMF is analyzed using the envelope demodulation. As shown in Fig. 7, it is obvious that the periodic impact frequency (100 Hz) and its harmonic (200 Hz, 300 Hz, 400 Hz, 500 Hz, etc.) of bearing fault can be seen. In order to verify the necessity of combining the two methods, the bearing simulation signals are not processed by MOMEDA, and the first IMF is obtained by applying ICEEMDAN directly. The envelope spectrum is shown in Fig. 8. The strong noise makes great difficulty in identifying the bearing fault periodic impact frequency clearly and accurately. Simulation analysis shows that the method is effective and suitable for early fault feature extraction of bearings under strong noise.
Fig. 7Envelope spectrum of IMF1 (processed with MOMEDA)
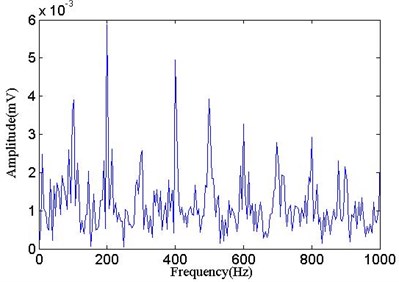
Fig. 8The envelope spectrum of IMF1 (not processed with MOMEDA)
5. Experimental verification
As shown in Fig. 9, the test stand consists of a 2 hp motor (left), a torque transducer and encoder (center), a dynamometer (right), and control electronics (not shown). The experimental bearings type is SKF 6205-2RS [13]. The bearing specifications are shown in Tables 1, 2. Single point faults were introduced to the test bearings using electro-discharge machining with fault diameters of 0.18 mm (depths 0.28 mm) at the inner raceway and outer raceway. The motor speed is 1730 r/min, and the sampling frequency is 12 kHz.
Fig. 9The schematic diagram of experimental device
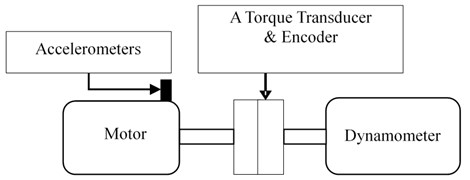
Table 1The bearing size
Ball diameter ( / mm) | Pitch diameter (/ mm) | Inside diameter ( / mm) | Outside diameter ( / mm) | Rolling element () | Contact angle ( / °) |
8 | 39 | 25 | 52 | 9 | 0 |
Table 2The bearing defect frequencies
Rotation frequency ( / Hz) | Ball pass frequency, inner race (BPFI / Hz) | Ball pass frequency, outer race (BPFO / Hz) |
28.83 | 156.12 | 103.35 |
The time-domain waveform of vibration signals of bearing inner and outer race and one enhanced by MOMEDA are shown in Fig. 10. After being enhanced the bearing vibration signals with MOMEDA, the inner race fault vibration signals’ kurtosis increases from 4.48 to 11.25, and the outer race fault vibration signals’ kurtosis increases from 3.06 to 11.81. Impact components are found in the time- domain waveform, but the bearing fault feature is still not clearly identified under the noise.
Then signals are decomposed by ICEEMDAN, and the result is shown in Fig. 11. Finally, IMF1 is demodulated to obtain the envelope spectrum, as shown in Fig. 12.
Fig. 10Time-domain waveform of bearing vibration signal
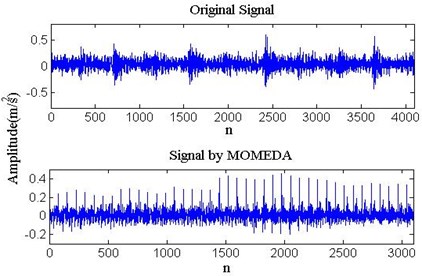
a) Inner race fault
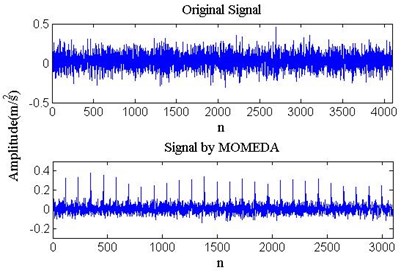
b) Outer race fault
Fig. 11Time-domain waveform of ICEEMDAN
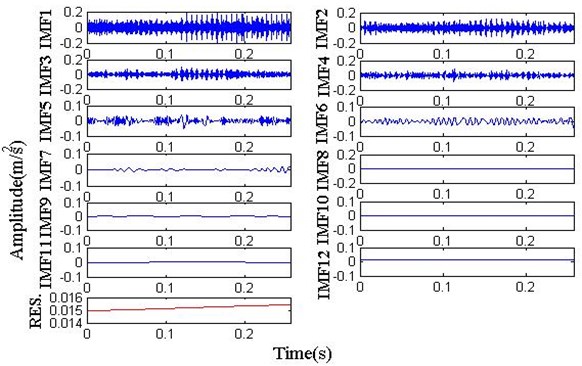
a) Inner race fault
b) Outer race fault
As can be seen from Fig. 12, the vibration signals of the bearing inner race fault include the BPFI and harmonics, sidebands spaced at , and the vibration signals of the bearing outer race fault include BPFO and harmonics. On account of speed fluctuation and rolling element rotation, the actual fault characteristic frequency is slightly lower than the theoretical one, which is normal. By comprehensive analysis, this method can be used for accurate diagnosis of bearing inner race fault and outer race fault, and the analysis results accord with the fact. To test the advantages of this method, three different methods in reference [14] (square envelope spectrum, cepstrum prewhitening, benchmark method) using the same bearing data, were unable to identify the bearing fault characteristic frequency (Without getting into repeating the description owing to space constraints). Therefore, the method based on MOMEDA and ICEEMDAN can accurately extract the weak fault feature of bearing and is of creativity and practical value.
Fig. 12The envelope spectrum of IMF1
a) Inner race fault
b) Outer race fault
6. Conclusions
Bearing impact feature is weak in the early fault period, and especially vulnerable to other signals. MOMEDA using a non-iterative process can deconvolve the signal, enhance the periodic pulse under strong noise, improve the kurtosis and SNR, and apply to enhancing the impact of bearing early fault period.
ICEEMDAN is a new adaptive approach to the decomposition of nonlinear and non-stationary signal. It can overcome the presence of spurious modes and residual noise in modes compared with the traditional mode decomposition (EMD, EEMD, CEEMDAN), and can accurately extract different frequency components of bearing fault vibration signals
References
-
Huang N. E., Shen Z., Long S. R., et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London. A, Vol. 454, Issue 1971, 1998, p. 903-995.
-
Chen J. X., Cheng L. S., Hu S. L., et al. Fault diagnosis for rolling bearings using modified Mahalanobis-Taguchi system. Journal of Vibration and Shock, Vol. 36, Issue 5, 2017, p. 151-156.
-
Zhao D. Z., Li J. Y., Cheng W. D. The method of rolling element bearing fault diagnosis based on IDMM and EMD under time-varing rotational speed and gear noise. Journal of Vibration and Shock, Vol. 35, Issue 10, 2016, p. 101-107.
-
Ma X. N., Yang S. P. Study of adaptive compound fault diagnosis of rolling bearing. Journal of Vibration and Shock, Vol. 35, Issue 10, 2016, p. 145-150.
-
Wu Z., Huang N. E. Ensemble empirical mode decomposition: a noise assisted data analysis method. Advances in Adaptive Data Analysis, Vol. 1, Issue 1, 2009, p. 1-41.
-
Liu Y. Q., Li C. X., Liao Y. Y. Fault diagnosis method of bearings based on EEMD and autocorrelation function kurtosis. Journal of Vibration and Shock, Vol. 36, Issue 2, 2017, p. 111-116.
-
Torres M. E., Colominas M. A., Schlotthauer G., et al. A complete ensemble empirical mode decomposition with adaptive noise. IEEE International Conference on Acoustics, Speech and Signal Processing, 2011.
-
Mohanty S., Gupta K. K., Raju K. S. Vibro-Acoustic Fault Analysis of Bearing Using FFT, EMD, EEMD and CEEMDAN and Their Implication. Springer-Verlag, New York, USA, 2016.
-
Colominas M. A., Schlotthauer G., Torres M. E. Improved complete ensemble EMD: a suitable tool for biomedical signal processing. Biomedical Signal Processing and Control, Vol. 14, Issue 2, 2014, p. 19-29.
-
Mcdonald G. L., Zhao Q. Multipoint optimal minimum entropy deconvolution and convolution fix: application to vibration fault detection. Mechanical Systems and Signal Processing, Vol. 82, 2017, p. 461-477.
-
Cabrelli C. A. Minimum entropy deconvolution and simplicity: a noniterative algorithm. Geophysics Vol. 50, Issue 3, 1985, p. 394-413.
-
Wang X. D., Zi Y. Y., He Z. J. Multiwavelet construction via an adaptive symmetric lifting scheme and its applications for rotating machinery fault diagnosis. Measurement Science and Technology, Vol. 20, Issue 4, 2009, p. 045103.
-
Case Western Reserve University Bearing Data Center Website, http://csegroups.case.edu/bearingdatacenter/home.
-
Smith W. A., Randall R. B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mechanical Systems and Signal Processing, Vol. 64, 2015, p. 100-131.
