Gearbox fault diagnosis method based on the fusion of EEMD and improved Elman-NN

1. Introduction

As the core component of mechanical transmission system, gearbox is widely used in various mechanical equipment [1]. Because the working environment of the gearbox is usually more complicated, long-term operation, coupled with the influence of various factors such as temperature and lubrication, the gears of gearbox are prone to pitting, broken teeth, and wear failures, and the gearbox bearings are prone to failures such as wear and bending. If the abnormality cannot be detected in time, long-term operation will cause damage or abnormal accumulation gradually, causing irreversible consequences. Therefore, it is necessary to monitor the status of the gearbox in real time, accurately determine the type and location of the fault, and maintain it in time to achieve the goal of minimizing the expected loss.

The empirical mode decomposition (EMD) method is a new time-frequency analysis method proposed by Huang, and it is an adaptive time-frequency localization analysis method [2]. EMD is superior to the Fourier transform method, yet the more important disadvantage of EMD is modal aliasing. In order to solve this problem better, Huang also proposed an improved EMD method, namely EEMD (Ensemble Empirical Mode Decomposition) method [3]. Because the gear fault signal is nonlinear and non-stationary, and the Elman-NN has strong nonlinear mapping and fault tolerance, it is especially suitable for nonlinear pattern recognition and classification, so it is introduced into fault diagnosis. Ayodeji [4] introduced an Elman-NN to perform nuclear power plant fault diagnosis, and the results show that the diagnosis method is feasible. Chemseddine [5] proposed a novel fault diagnosis method for gearbox system based on the fusion of HEWT-SVD and Elman-NN. The results show that the diagnostic performance of this method is better than (HHT)-SVD, (LMD)-SVD and (WPT)-PCA methods. Baraldi [6] developed a fault diagnosis method based on Auto-Associative Kernel Regression, Fuzzy Similarity and Elman Recurrent NN. This combined method can overcome the limitations of these three independent methods. Considering that the standard Elman-NN can only identify the first-order dynamic model, as the hidden layer or the order of the system increases, its dynamic memory and association capabilities are significantly weaker. Based on the advantages of the EEMD method and the shortcomings of the standard Elman-NN, this paper puts forward a gearbox fault diagnosis means based on the fusion of EEMD and the improved Elman-NN.

2. Extraction of effective IMF components based on EEMD method

EEMD is an improved algorithm of EMD, which can overcome the modal aliasing phenomenon caused by non-white noise interference generated by EMD algorithm [3]. After the initial signal is decomposed by EEMD, due to multiple factors such as decomposition error and interpolation error, the IMF component in the decomposition result is prone to false components. If the false component exists in the feature domain, it will obviously cause a large error in the extracted degradation performance index. Therefore, it is very necessary to remove the false component. Considering that the correlation between the false component and the initial signal is small, the false component can be distinguished by introducing a correlation coefficient. We can make the mathematical expression of the correlation coefficient be described as follows:

where ${\lambda }_j$ ($j=$1, ..., $l$) are the correlation coefficients between all IMF components and the original signals; $x$ and $\stackrel{-}{x}$ represent respectively the initial signal and its average value; $y$ and $\stackrel{-}{y}$ represent respectively the IMF component signal and its average value; $n$ represents the number of acquisition data samples of vibration signal.

Then, set the threshold value $\mu$ for distinguishing false components. If the correlation coefficient between the IMF component and the initial signal is less than the $\mu$, it will be removed. Finally, the IMF components larger than the $\mu$ will be retained and reconstructed, so as to obtain an effective initial signal to achieve a reduction of noise.

3. The improved algorithm of Elman-NN

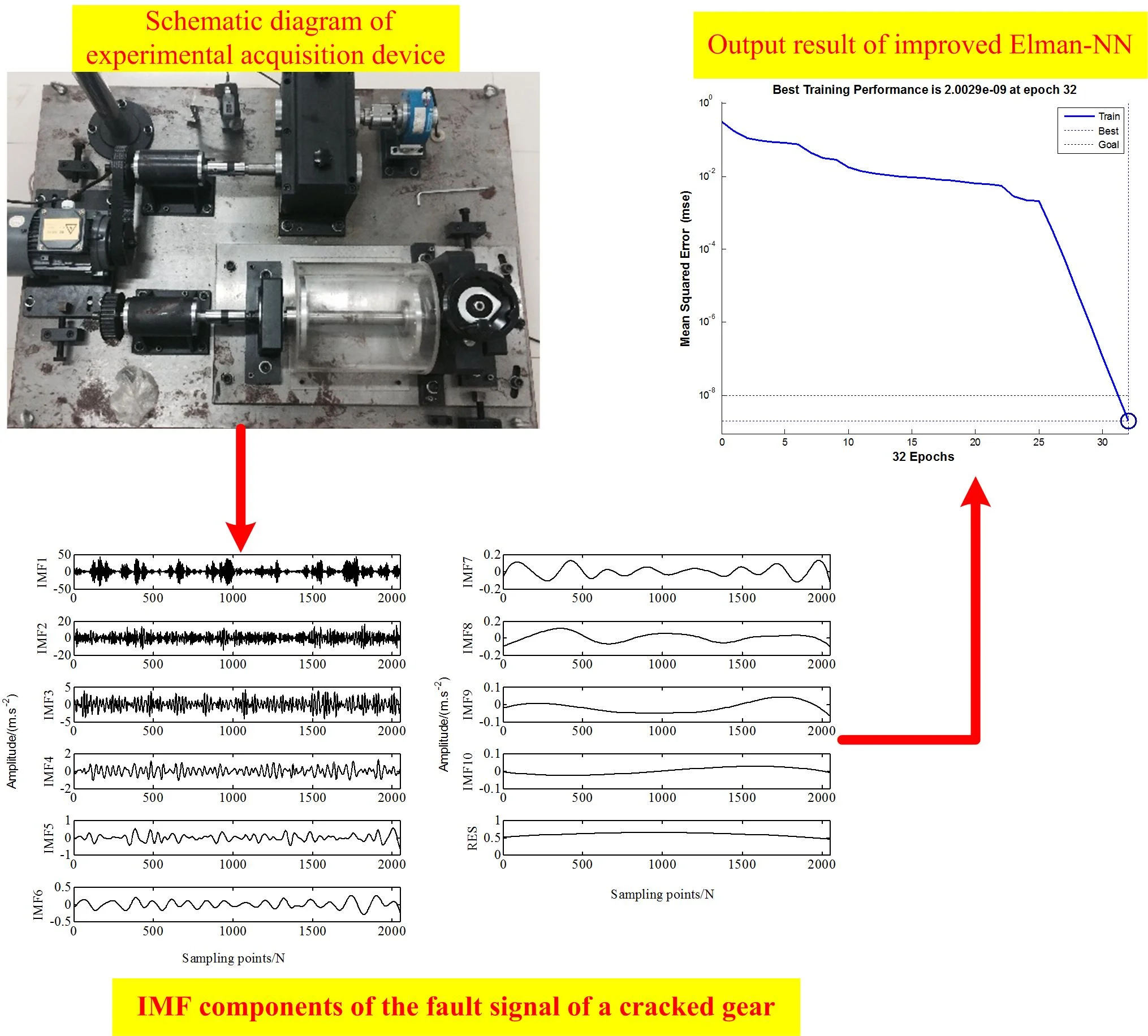
Elman-NN is a feedback neural network (NN), a typical localized regression network, a forward NN which is provided with localized memory units and localized feedback connections. The standardized Elman-NN uses the BP algorithm, which can only identify first-order dynamic models. When the hidden layer or the order of the system increases, its dynamic memory and association capabilities are limited. To this end, this paper uses a reformed Elman-NN to analyze and diagnose multiple failure modes of asynchronous motor rolling bearings. The improved Elman-NN adds a self-feedback factor $\beta$ ($\beta \in$[0, 1]) on the basis of the standard network. That is, mutual feedback and self-feedback are introduced between nodes in the same layer of feedforward network, which makes this network better achieve the recognition of non-linear mapping pattern, while the self-feedback link of correlated nodes also largely streamlines the network scale and improves the learning speed. The structure of improved Elman-NN structure is shown in Fig. 1. When $\beta$ is close to 1, it indicates that it can contain more distant info. When $\beta$ is equal to 0, this reformed Elman-NN degenerates into a standardized Elman-NN.

Suppose that $X$ which is the input vector of the whole network is $r$-dimensional, $Y$ which is the output vector is $m$-dimensional, $Y_J$ which is the output vector of the hidden layer and $Y_L$ which is the output vector of the successor layer are $s$-dimensional. The mathematical model which belongs to the improved Elman-NN [7] is described as follows:

Eq. (4) is used to obtain partial derivatives of $w_{oj}$, $w_{ji}$, and $w_{jl}$ and set them to 0. Finally, the learning algorithm which belongs to the reformed Elman-NN is obtained:

where $w_{oj}$, $w_{ji}$, and $w_{jl}$ respectively denote the $j$th node in the hidden-layer to the $o$th node in the output-layer, the $i$th node in the input-layer to the $j$th node in the hidden-layer, and the $l$th node in the inheriting layer to the $j$th node in the hidden-layer. While $g(•)$ and $f(•)$ respectively represent activation functions of the output-layer neurons and the hidden-layer neurons. $out\left(\right)$ represents the output of input-layer; $net\left(\right)$ represents the net input of a certain layer; $I$ represents the input-layer; $J$ represents the hidden-layer; $L$ represents the receiving layer; $O$ represents the output-layer; $y\left(k\right)$ represents the real output of network; $y_d\left(k\right)$ is the expected output; $E$ represents the error objective function; $k$ is the iteration order. ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$ respectively represent the learning steps of $w_{jl}$, $w_{ji}$, and $w_{oj}$, ${\delta }_i$ and ${\delta }_j$ are respectively denoted as the deviation values of the $i$th node in output-layer and the $j$th node in hidden-layer.

Fig. 1The improved structure of Elman-NN

4. Experiment analysis

4.1. The collection of experiment data

The experiment device is shown in Fig. 2(a). The included hardware mainly includes the QPZZ-II fault diagnosis test platform system, several acceleration sensors, two data collectors, and one signal conditioner. The small gear of this experiment platform is the driving wheel, which the motor shaft is connected to; the big gear is the driven wheel, which the magnetic powder brake is connected to through a coupling. Paste a circle of black tape on the driving shaft (leaving a slit of about 2 mm to reflect light), and use an infrared speedometer to measure the shaft speed. The number of teeth of the pinion is 55; the number of teeth of the big gear is 75. And two acceleration sensors are respectively installed in vertical and horizontal directions of the big gear outside the gearbox. The calibration values of these two sensors are respectively 99 mV/g and 102 mV/g. The layout of measuring point is shown in Fig. 2(b).

A dual-channel data collector is used to collect normal signals and three typical fault signals of cracks, broken teeth and wear. To ensure that enough data samples are collected, the sampling frequency must be 2.56 or more times of the analysis frequency.

Fig. 2Schematic diagram of experimental acquisition device

a) Schematic diagram of experimental platform

b) Schematic diagram of measuring point layout

4.2. Signal denoising and effective signal screening

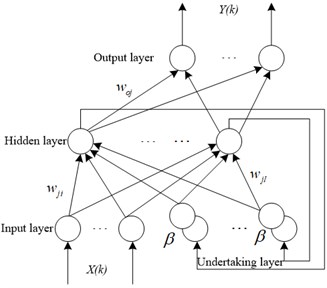
The wavelet packet method is utilized to denoise the normal signal and the three typical fault signals of cracks, broken teeth, and wear. Then use EEMD to decompose the signals, and set the Nstd in the EEMD algorithm to 0.2, and add 1000 times of Gaussian white noise, then we get 1 margin and 10 IMF components, as shown in Fig. 3. Finally, use the correlation coefficient criterion shown in Eq. (1) to screen the effective IMF components. In the screening, set the correlation coefficient threshold $\mu =$0.15, and the correlation coefficients of IMF1, IMF2, and RES are all less than 0.15, so they are eliminated. The remaining components are reconstructed to obtain the effective signal after screening.

Fig. 3IMF components of the fault signal of a cracked gear

4.4. The analysis of diagnosis result

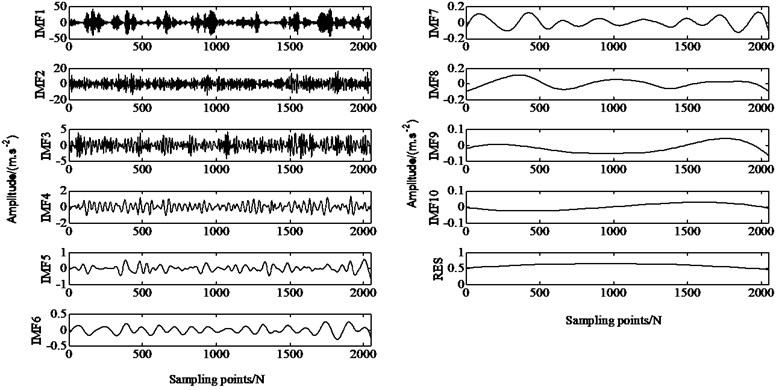
There are 4 types of gearbox faults studied in this paper: broken gear tooth fault (1, 0, 0, 0), crack fault (0, 1, 0, 0), wear fault (0, 0, 1, 0), no fault (0, 0, 0, 1). In order to facilitate comparison, the structural parameters of the Elman-NN before and after the improvement are basically the same. The selection is as follows: the number of input neurons is 4 (energy characteristics of 4 frequency bands), and the output neurons are 4 (4 failure types). The transfer functions belonging to hidden layer and output layer are respectively set as tansig and logsig functions, the number of training is set to 1000, the index minimum mean square error is set to 10^-10, and $\beta =$0.38. Fig. 4 and Fig. 5 are the training conditions of Elman-NN before and after improvement. The standard Elman-NN needs to be trained for 83 steps to achieve the set average square error, the diagnosis time is 0.4038 seconds, and the diagnosis error is 1.0e-07×[0.0038, 0.0025, 0.5413, 0.0040]. The informed Elman-NN just needs to train 32 steps to achieve the set average square error, the diagnosis time is 0.3204 seconds, and the diagnosis error is 1.0e-07×[0.0002, 0.0517, 0.1469, 0.0039]. From the result, it is not difficult to see that the improved Elman-NN can effectively diagnose different types of gear faults, but the improved Elman-NN has shorter diagnosis time and higher diagnosis accuracy.

Fig. 4Output result of standard Elman-NN

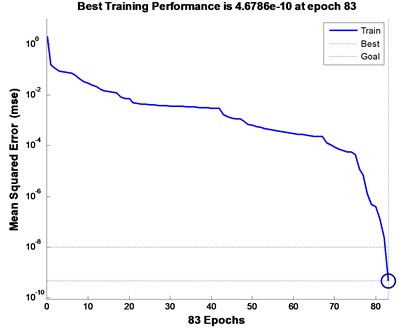
a) Number of iterations

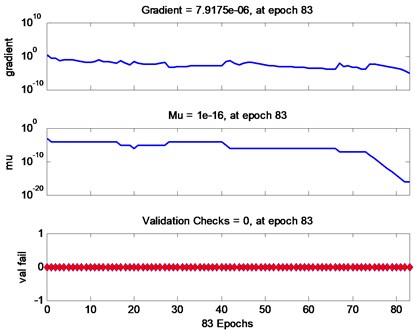
b) Training process

Fig. 5Improved Elman-NN

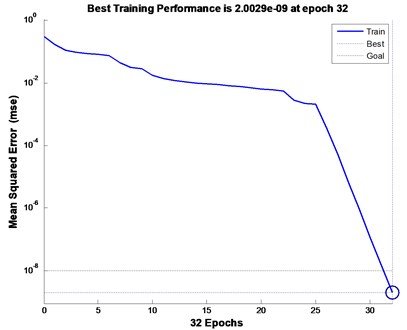
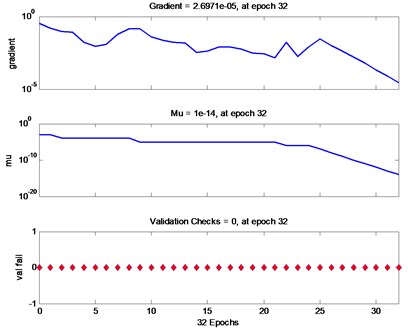
5. Conclusions

In this work, in order to more efficiently and accurately identify broken teeth, cracks, wear and normal gear conditions involved in the gearbox, a fault diagnosis method based on the fusion of EEMD and improved Elman-NN is introduced. Through the EEMD decomposition of gear vibration signals of different types of failures, the correlation coefficient criterion method is utilized to implement effective IMF component screening, to obtain more pure vibration information. In order to build the Elman-NN with faster learning speed, I add a feedback factor to the standardized Elman-NN to make the network realize the pattern recognition of nonlinear mapping better. And to a large extent, the self-feedback connection of the correlated nodes simplifies the scale of the network. Therefore, the learning speed of the network is improved. The analysis results of experiment indicate the improved Elman-NN diagnosis system has the characteristics of higher accuracy and shorter diagnosis time.