Prediction of dynamic deformation development of soil using Gompertz curve

2.1. Gompertz curve

Gompertz curve is originally used to describe the prediction of species number in nature and it is widely applied to the analysis of population growth control. Till now, its application scope is not limited to biological models. Practices show that Gompertz curve has been widely used in market forecasting [8], settlement in engineering [9, 10] and even traffic prediction.

Gompertz curve initially describes the relationship between population size and time; its basic form is, $\frac{d_y}{d_t}=-Ty\mathrm{l}\mathrm{n}\frac{y}{k}$. It can be solved from above equation, $y=K{\left(\frac{y_0}{K}\right)}^{e^{-Tt}}$. Generally, the end of the curve is written as $y=K{a}^{b^t}$.

Where, $a=\frac{y_0}{K}$, $b=\mathrm{e}\mathrm{x}\mathrm{p}(-T)$, a and b are model parameters; $y$ is the population size; $K$ is the environmental capacity; $y_0$ is thinitial population number, $T$ is the growth coefficient of population, and e is natural constant.

2.2. Establishment and deduction of Gompertz model

The dynamic deformation curve of soil and Gompertz curve have similar development law. According to the practical significance of the dynamic deformation curve of soil and Gompertz curve, the Gompertz model applied to the dynamic deformation curve is derived as follows:

The relationship between the dynamic strain and cycle number (vibration times) of the soil was established by Gompertz model. Among them, ${\epsilon }_p$ is the dynamic strain of soil; $K$ is the maximum dynamic strain of soil; $N$ is the cycle number (vibration times), a and b are model parameters.

3.1. Test instrument

The test instrument adopts SDT-10 microcomputer controlled electro-hydraulic servo of soil dynamic triaxial test machine, and the instrument is composed of load control system, loading system and data acquisition system, detailed as axial loading mechanism and frame, confining pressure imposing mechanism, pressure chamber, pressure chamber lifting mechanism, hydraulic oil source, electrical control, microcomputer display, control and data processing.

Fig. 1SDT-10soil dynamic triaxial test machine with microcomputer control

3.2. Sample preparation and test scheme

The soil sample was taken from the excavation of the back edge of a landslide in the reservoir area of a hydropower station (shortened as Badong soil). The soil samples were yellowish and slightly expansive, and the main physical properties of the soil samples are shown in Table 1. Its plastic limit index $I_p=$16.88, silty clay, liquid limit index $I_L<$ 0, the soil in the natural state is a hard state.

The sample takes three valves as mould and divided into four layers, and triaxial test samples are prepared using layered compaction method. The diameter is 61.8 mm and the height is 120 mm. After the sample is prepared, it is put into vacuum saturated cylinder and saturated by vacuum saturation method. Relevant studies have shown that the soil properties would experience irreversible changes after dry-wet cycles, reaching stable after five dry-wet cycles [12, 13]. The soil would experience several dry-wet cycles with the rise and fall of reservoir water level and climatic factors. In order to simulate the state, the saturated solid samples including saturated frame are dried in a constant temperature drying box, and the natural state temperature is set to 35 centigrade in order to simulate the natural state; control its water content change at about 10 % and then immerse in distilled water till to close to saturation. This process is a dry-wet cycle. For each sample, 0, 1, 3 and 6 dry-wet cycles were carried out respectively.

The prepared samples are used for isotropic consolidation test. Firstly, 10 kPa lateral pressure is added to the samples, and then equal lateral pressure ${\sigma }_{3c}$ and axial pressure ${\sigma }_{1c}$, till equal lateral pressure ${\sigma }_{3c}$ and axial pressure ${\sigma }_{1c}$ are equal and reach setting pressure. Undrained dynamic test is carried out after consolidation test, the applied confining pressure of the test is 300 kPa; amplitude of dynamic stress is 150 kPa and 50 thousand cycle vibrations in all.

3.3. Test results and analysis

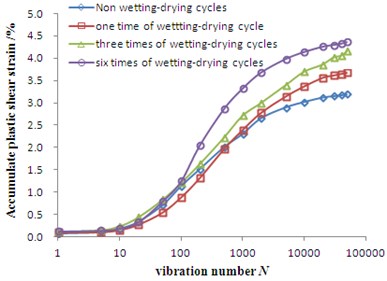
Fig. 2 is the dynamic deformation curve of Badong soil test. It is found that the dynamic deformation curve of Badong soil is stable under the conditions of 300 kPa confining pressure, 150 kPa amplitude of dynamic stress and different dry-wet cycles. When the loading and unloading cycles are less than 50 times, the soil dynamic strain changes little. When the loading and unloading times reach 50 times, the dynamic strain of soil increases sharply to about ten thousand times and then tends to be stable again. And then the increase of loading and unloading times has little effect on the dynamic strain of soil. At the same time, compared with the experimental curves under different dry-wet cycles, it is found that the dynamic strain has increasing trend with the increase of dry-wet cycles.

Fig. 2Relationship between accumulative plastic strain and vibration amplitude of Badong soil under different drying-wetting cycles

4.1. Study on the dynamic deformation of Badongsilty clay using Gompertz model

It can be seen from Fig. 2 that the test curves of Badongsilty clay are all stable curves under the conditions of 300 kPa confining pressure, 150 kPa dynamic stress amplitude, 0, 1, 3 and 6 times of dry-wet cycle. Gompertz model can be used to fit the dynamic strain, and the confidence band range of the model at 95% confidence level is given. The results are shown in Fig. 3.

Fig. 3Fitting curves of measured data and predicted data under different dry-wet cycles in Badong soil

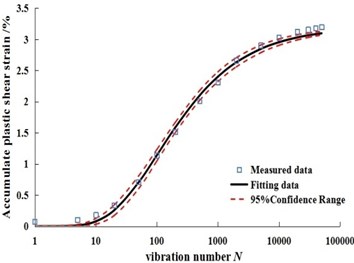
a) Zero time of dry-wet cycle sample

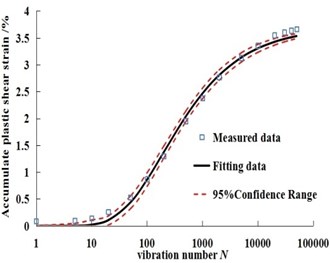
b) One time of dry-wet cycle sample

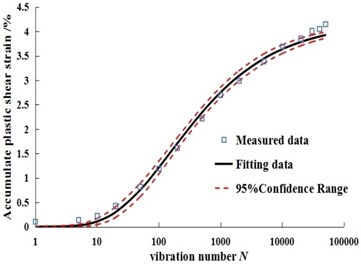
c) Three times of dry-wet cycle sample

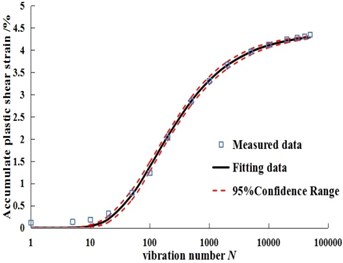
d) Six times of dry-wet cycle sample

4.2. Study on dynamic deformation of silty clay in Dalian using Gompertz model

Liu Wenhua et al. [14] made soil dynamic test to the silty clay in Dalian. The confining pressure of saturated samples during the test was 50 kPa; the samples experienced zero and six time(s) of dry-wet cycle respectively and comparison test was carried out. The sample with zero time of dry-wet cycle selects the dynamic deformation curve with 100 kPa dynamic stress amplitude, and the sample with six times of dry-wet cycles selects the dynamic deformation curve with 110 kPa dynamic stress amplitude, and the two curves are both stable shown as Fig. 4. From the experimental data, it is found that the cumulative plastic strain of Dalian soil increases with the increase of loading and unloading times, and the cumulative plastic strain decreases with the increase of the number of dry-wet cycles.

Gompertz model is used to calculate the dynamic strain, and the confidence band range of the model at 95 % confidence level is given. The results are shown in Fig. 5.

Fig. 4Relation curves between cumulative plastic strain and vibration amplitude under different dry-wet cycles in Dalian soil

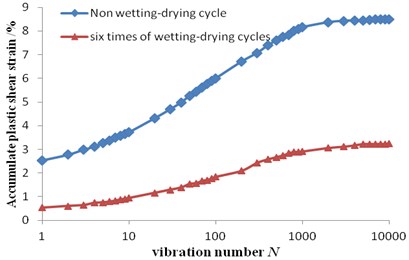
Fig. 5Fitting curves of measured data and predicted data under different dry-wet cycles in Dalian soil

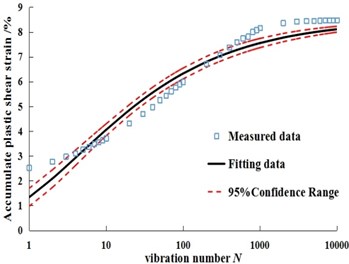
a) Original samples

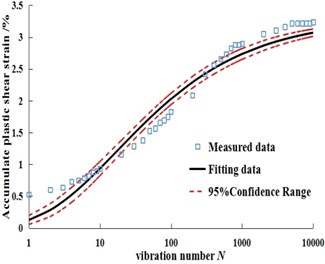
b) Six times of dry-wet cycles samples

4.3. Application results and analysis of Gompertz model

The traditional dynamic strain curve is displayed in a constant coordinate. The commonly used model is found to be fitted by exponential function shown as [15]:

Comparatively, Gompertz model adds the factor of maximum dynamic strain, not only from the curve shape, but also from logarithmic coordinates to analyze the dynamic strain curve of soil, which can better reflect the relationship between dynamic strain and loading and unloading times. From the fitting results of Gompertz model for dynamic strain and the distribution state of confidence band in Fig. 3 and Fig. 5, the real value is basically within the 95 % confidence band of the fitting curve, which indicates that Gompertz model can better describe the evolution characteristics of dynamic strain and loading and unloading times under different dry wet cycles; At the same time, combined with the average absolute error (MAE) and mean square error(RMSE) of the two soils in Table 2, the two error indexes are less than 0.5, and Badong soil has the lowest error result. It shows that the discreteness of the model curve is low, the degree of deviation from the real value is very small, and the accuracy of the model is high. The curve fitting parameters and fitting degree are shown in Table 2.