Acoustic vibration analysis of high-temperature thin-walled structures

2.1. Governing equations of thin plate under thermal-acoustic loads

The well-known von Karman large deflection equation with thermal and acoustic loads can be derived by the analysis of forces and moments in the plate:

where $D$ is bending stiffness, $h$ is the thickness of the plate, $\mu$ is Poisson ratio, $\theta$ is the temperature gradient along $h$, $p\left(x,y,t\right)$ is the random pressure used to simulate acoustic load, $\mathrm{\Phi }$ is Airy stress function, $w$ is transverse deflection of the middle plane.

The corresponding strain compatibility equation can be represented as:

where $E$ is Young’s modulus, ${\nabla }^4$ is bi-harmonic operator, $\stackrel{-}{T}\left(x,y\right)$ is average temperature along the plate thickness $h$.

2.2. FEM equation of thin plate under thermal-acoustic loads

It’s very difficult to directly solve Eq. (1) and Eq. (2), which can be discretized into dynamic FEM equation as:

where, $\mathbf{M}$ is the mass matrix, $\mathbf{C}$ is the damping matrix, ${\mathbf{K}}_L$ is the linear stiffness matrix, ${\mathbf{N}}_1$ and ${\mathbf{N}}_2$ are first-order and second-order nonlinear stiffness matrices respectively, $\mathbf{X}$ is the displacement vector, ${\mathbf{F}}_p$ is the acoustic load vector, The influence of thermal load is reflected on both sides of Eq. (3), i.e. ${\mathbf{K}}_T$ represents the stiffness term induced by thermal stress, and ${\mathbf{F}}_T$ is the thermal load vector.

The above stiffness terms can be combined into one term, and the same applies to the load terms, so Eq. (3) takes the simplified form as:

By employing the Newmark-Beta integration method, the dynamic response of the thin plate under the combined thermal-acoustic loads can be simulated.

2.3. Determination of thermal-acoustic loads

This paper assumes that the thermal load on the thin plate is a uniformly distributed temperature field, and there is no temperature gradient considered. The buckling coefficient can be prescribed as:

where $T_{ref}$ is the ambient temperature, $T_{cr}$ is the critical buckling temperature.

The acoustic load is a band-limited Gaussian white noise excitation, with its amplitude following the zero-mean Gaussian distribution and its power spectral density (PSD) that is uniformly distribution. The effective value of the sound pressure is:

The PSD can be given by:

where $\mathrm{\Delta }\omega ={\omega }_u-{\omega }_l$ is band-width represented by angular frequency.

3.1. Analysis model

This paper adopts the sequentially coupling method to address the thermal-acoustic vibration problem. A typical aluminum alloy thin plate is selected as the research model, which had clamped boundary conditions at both short edges. The length, width, and height of the plate are 457 mm, 25 mm and 2.3 mm, respectively. The material parameters are Young’s modulus $E=$7.3×10¹⁰ Pa, density $\rho =$2763 kg/m³, Poisson’s ratio $\mu =$0.3, and linear expansion coefficient $\alpha =$22.3×10^-6 °C.

3.2. Thermal buckling analysis of thin plate

Using Galerkin’s approach, the large deflection equation Eq. (1) can be reduced to a second-order ordinary differential equation in modal coordinates. In order to illustrate the basic characteristic and explain the mechanism of snap-through, the non-dimensional single-mode plate equation can be derived as:

where, $q$ is the generalized coordinate of displacement in $w(x,y,t)=q\left(t\right)h\mathrm{s}\mathrm{i}\mathrm{n}\pi x\mathrm{s}\mathrm{i}\mathrm{n}\pi y$, $k=4A$, $A=\frac{3}{4}\left[\right(1-{\mu }^2\left)\right(1+{\beta }^4)+2({\beta }^4+2\mu {\beta }^2+1\left)\right]$, $\beta$ is the aspect ratio of the plate, i.e. the ratio of length to width of the plate, $\xi$ is the damping ratio, and $p^d\left(t\right)$ is the acoustic load.

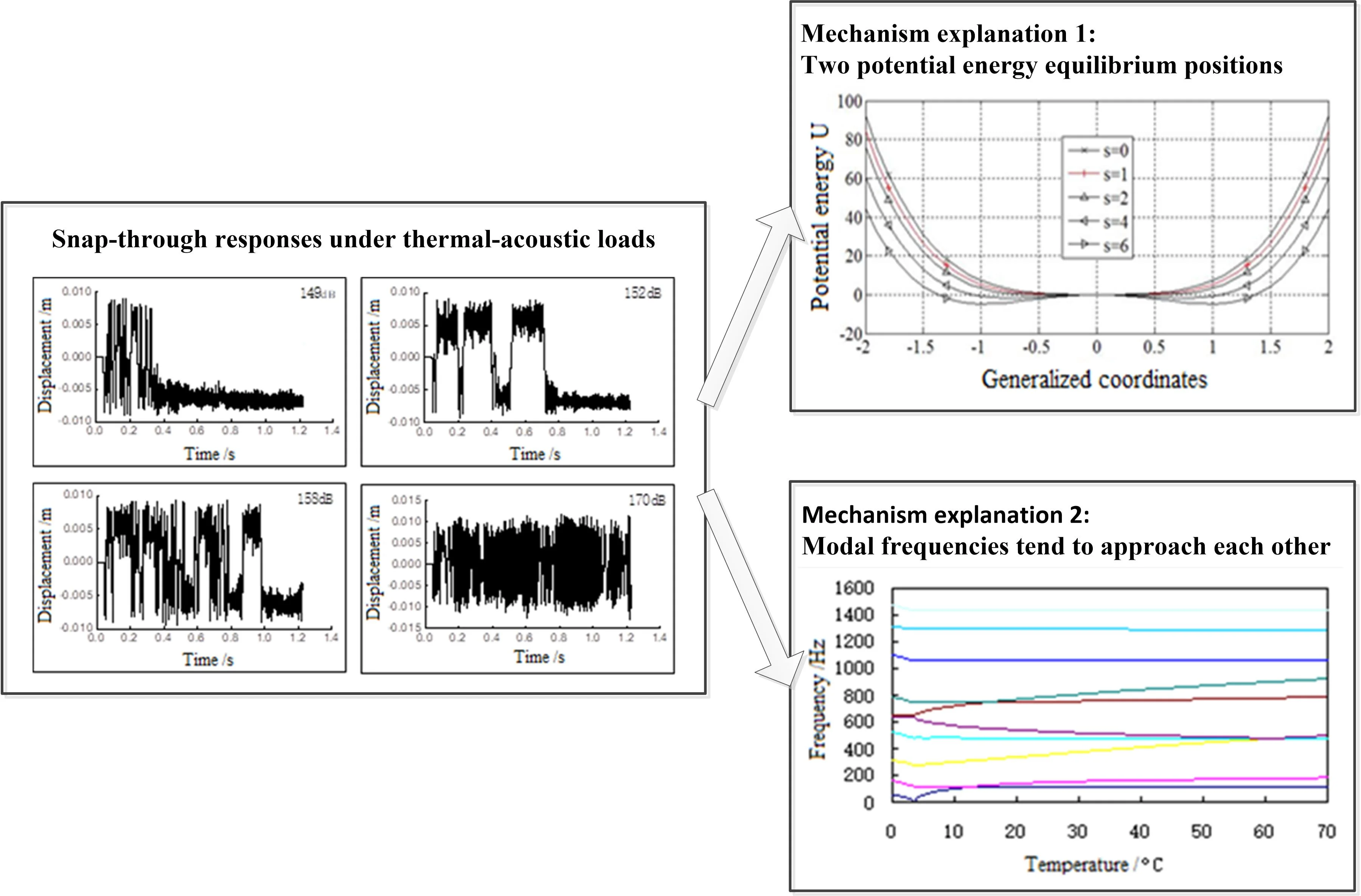
The potential energy of Eq. (8) can be given by:

When $\mu =\text{0.3}$, $\beta =\text{1.4}$, and $s=$1, 2, 4, 6, the potential energy changes as shown in Fig. 1. According to Eq. (9) and Fig. 1, when $0<s<1$, the potential energy curve has a single minimum position, indicating that the thin plate has only one stable equilibrium position. However, when $s>1$, the thin plate enters thermal buckling state, and the potential energy curve has two lowest positions, implying that the thin plate has two stable equilibrium positions. These two equilibrium positions are symmetric about the initial geometrical configuration. This means that when the SPL of external acoustic load excitation is small, the thin plate may keep a small vibration near one of the two equilibrium positions. As the SPL of acoustic load increases to a certain level, vibration of the thin plate would shuttle back and forth between the two equilibrium positions, resulting in snap through phenomenon.

When the SPL exceeds the level required for snap-through, but is not too high, there are some random and intermittent short time periods due to the randomness of the acoustic load. At this time, the SPL is not sufficient to drive the vibration of the plate to jump to another equilibrium position without snap-through happened, which means the plate can only vibrate at one equilibrium position with small amplitude. Conversely, there are also some random and intermittent short time periods, during which the SPL has ability to drive the large amplitude vibration of the plate to jump to the other equilibrium position with snap-through happened. We call the above vibration as intermittent snap-through.

If the SPL is high enough, high-intensity acoustic load has sufficient ability to drive the plate to vibrate significantly between two equilibrium positions at any time. In this case, the vibration response is called continuous snap-through.

Fig. 1Potential energy

3.3. Thermal modal analysis of thin plate

In pre-buckling state of the plate, the in-plane thermal stress caused by the temperature rise decreases the stiffness of the structure. Thermal buckling occurs at the critical buckling temperature $T_{cr}$, which leads to a decrease in structural stiffness to zero. Then, as the temperature continues to rise, unrecoverable buckling deflection will be arised, and the plate will enter post-buckling state. In post-buckling stage, the structural stiffness will increase to a certain extent.

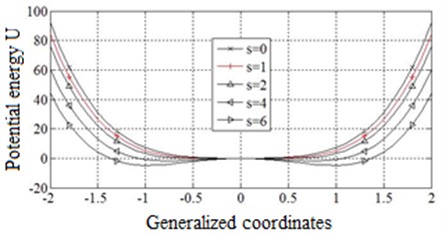
The critical buckling temperature of the thin plate has been calculated to be $T_{cr}=$3.76 °C with setting the reference temperature $T_{ref}=$0 °C. The first 3 modal shapes for pre-buckling with $s=$0, post-buckling with $s=$5.45 and 19.07 are shown in Fig. 2. The modal shapes are significantly different between pre-buckling and post-buckling, especially in higher order modal shapes at more serious post-buckling state. The 3rd modal shape has become a bending-torsion coupling mode, which means higher order modes would impact the dynamic thermal-acoustic response.

The first 10 modal frequencies are shown in Fig. 3. In general, the modal frequencies decrease with the increasing temperature before thermal buckling, and reach their minimum values at critical buckling temperature (the 1st frequency is 0). After thermal buckling, due to the influence of thermal hardening effect, the frequencies increase with the temperature further rising. Moreover, the modal frequencies tend to approach each other as the temperature rising in post-buckling, which implies resonance would be induced at the concentrative frequencies and the dynamic snap-through response may be occurred.

Fig. 2First three modal shapes of thin plates under different buckling coefficients

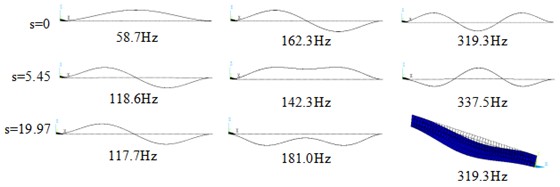
Fig. 3Changes in the first ten modal frequencies of the thin plate

3.4. Thermal-acoustic vibration response of thin plate

In simulated condition settings, taking the reference temperature and the structural temperature as 0 °C and 19.44 °C respectively, the structural temperature, corresponding $s=$5.17, is loaded linearly on the plate within 0.3 seconds, and the acoustic load is loaded on the plate in the whole simulated time period of 1.224 seconds. Dynamic responses of the thermal plate are obtained under SPLs of 149 dB, 152 dB, 158 dB, and 170 dB in the time domain. The transverse displacements of the midpoint in plate under different SPLs are shown in Fig. 4.

Fig. 4Time history displacements of the thin plate under different sound pressures

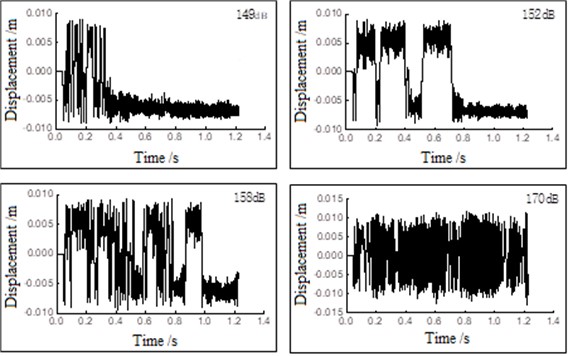
It can be seen that the vibration of the plate takes place only around a single equilibrium position with the SPL of 149 dB and there is no snap-through. When the SPL increases to 152 dB, the plate not only vibrates slightly around each equilibrium position, but also shuttles back and forth intermittently between the two balanced positions. The intermittent snap-through response occurs in this case, resulting in the reversed stress that weakens the fatigue life of the structure. When the SPL rises to 158 dB, although it’s still intermittent snap-through at this time, the frequency of snap-through significantly increases. At last, a continuous snap-through response occurs when the SPL is up to 170 dB.