Dynamic response of long-span continuous curved box girder bridge under seismic excitation

2.1. Fundamental assumption

In order to simplify the spatial mechanical model of a curved box girder, the following assumptions are to be made:

(1) Material is of linear elastic.

(2) Distortion and warping of box girder are not considered.

(3) The size of curved box girder cross section is of small magnitude compared with its length and curvature radius.

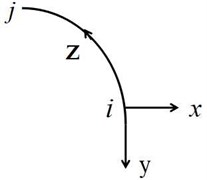
Curved box girder is shown as Fig. 1, $x$, $y$, $z$ are respectively represent transverse, vertical and longitudinal direction, element node displacement is shown as follows:

where $i$, $j$ are node serial numbers, $u$, $v$, $w$ are respectively longitudinal, vertical and transverse displacement, $\varphi$, $v\text{'}$, $w\text{'}$ are respectively torsion angle, vertical angle and transverse angle, $w\mathrm{\text{'}}\mathrm{\text{'}}$ is transverse curvature, $\beta$ is restricted distortion displacement, $\zeta$ is maximum shear displacement, this parameter is necessary for considering shear lag effects.

Fig. 1Curved box girder

2.2. Stiffness matrix

According to the geometric equation of elastic mechanic, generalized strain$\mathrm{\epsilon }$is given by:

The matrix form is shown as follows:

where the first matrix-vector in the right side is differential operator $\left[P\right]$, the second matrix-vector is generalized displacement vector $\left[\delta \right]$, therefore, it can be denoted as $\epsilon =\left[P\right]\left[\delta \right]$.

Transverse displacement is interpolated by fifth polynomial, vertical displacement and torsion angle are interpolated by third polynomial, longitudinal displacement is interpolated by linear interpolation [21], therefore, the form function matrix $\left[N\right]$ can be obtained.

The displacement of the element can be obtained from the following equation:

where ${\left[\mathrm{\delta }\right]}^e$is the element node displacement. Subsequently, Eq. (3) is substituted into Eq. (4), the following equations can be obtained:

here, $\left[P\right]\left[N\right]=\left[B\right]$, $\left[B\right]$ is strain matrix, elastic matrix $\left[D\right]$ is given by:

where $E$, $G$ are elastic modulus and shear modulus, $I_x$, $I_y$ are vertical and transverse inertial moment, $I_d$, $I_w$ are free torsion and restraint torsion inertial moment. The stress in the element is shown as follows:

The virtual strain of element is given by:

The work done by the stress for the virtual strain is shown as follows:

Meanwhile, the work done by the nodal force for a virtual displacement is shown as follows:

According to the virtual work principle [22], the nodal force column matrix $F^e$ can be obtained when the equation $\delta W_1=\delta W_2$ is substituted into Eq. (9) and Eq. (10):

The element matrix is obtained from Eq. (11) and it is shown as follows:

2.3. Mass matrix

Considered that the mass center does not coincide with the torsion center in the box girder cross section, the transverse inertial force of box girder is given by:

where $\rho$ is the density of box girder, $e$ is the distance from the mass center to the torsion center. The transverse inertial force will also contribute to an additional torsion moment, which is given by:

here, $I_{\rho }$ is the polar inertia moment, all inertia forces of box girder are shown as follows:

The corresponding matrix form is shown as follows:

where the first matrix-vector in the right side is denoted as matrix $\left[Q\right]$. Substituting the equation $\left[\ddot{\delta }\right]=\left[N\right]{\left[\ddot{\delta }\right]}^e$into Eq. (16) results in:

The equivalent nodal force is given by:

Substituting Eq. (18) into Eq. (17) results in:

The mass matrix $\left[M\right]$ can be obtained from Eq. (19) and it is shown as following equations:

2.4. Earthquake mass matrix

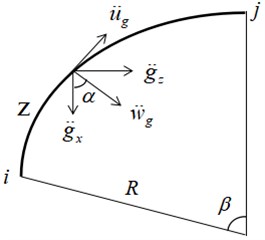
As is shown in Fig. 2, the ground acceleration is decomposed in 3 directions and it is given by:

Seismic action of curved box girder is given by:

Fig. 2Decomposition of ground acceleration

Substituting Eq. (22) into Eq. (23) results in:

where the third term of the right side is denoted as matrix $\left[J\right]$, therefore equivalent seismic action of the element is given by:

According to Newton’ second law, earthquake mass matrix is shown as follows:

There is a geometrical relationship in Fig. 2:

Then, the following equations can be obtained:

Eq. (28) is expanded based on Taylor series (only the first two entries are used), the earthquake mass matrix can be obtained when substituting Eq. (28) into Eq. (26):

3.1. Free vibration characteristics

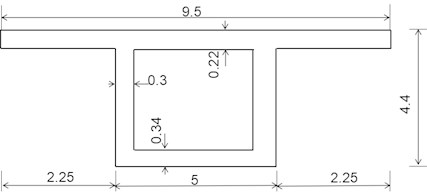
A PC continuous curved box girder bridge with three spans is shown as Fig. 3. The longitudinal span is of 210 m, curvature radius $R=$ 300 m, elasticity modulus $E=$ 3.4×10⁶ MPa, density $\rho =$ 2500 kg/m³. The cross section size of box girder is shown as Fig. 4.

Fig. 3Three-span curved box girder bridge (Unit: m)

Fig. 4Cross section size of box girder (Unit: m)

Vibration equation of curved box girder bridge is shown as follows:

where $\omega$ is vibration frequency, Eq. (30) has a nonzero solution when the curved box girder bridge vibrates freely, the following equations can be obtained:

The vibration frequency can be acquired when introducing corresponding boundary conditions according to Eq. (31). Attention should be paid that flow cylindrical coordinate system is adopted in the present work, therefore it is unnecessary to transform the element matrix.

The mesh of the curved box girder bridge along the longitudinal direction at each span contains 2, 3 and 4 elements, respectively and the eigenvalue equation is solved through MATLAB. Meanwhile, a finite element model is established by ANSYS, the primary beam is simulated by SHELL 63 element and the piers are simulated by SOLID 45 element, TARGE170 3D element and CONTA175 element are used to simulate the supports. There are totally 9660 elements and 9706 nodes in the finite element model. According to Chinese code JTG D60-2015 [23], estimation formulas of the natural vibration frequency of continuous beam bridge are shown as following equations:

where $l$ is the span $E$, $I_c$ are elastic modulus and inertia moment $m_c$ is linear mass $f_1$, $f_2$ are the first 2th order frequencies. Theoretical value and ANSYS results are shown in Table 1 and Fig. 5.

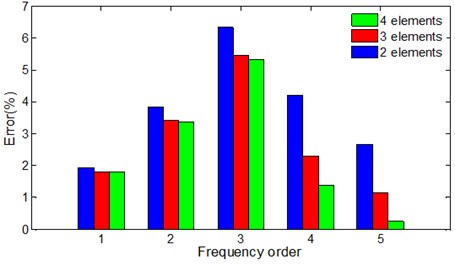
Fig. 5Influence of element number on error

From Table 1, the theoretical values present a good agreement with the ANSYS numerical results, satisfied results can be obtained when each span of the whole bridge is meshed with 3-4 elements, the computing time is greatly reduced compared with ANSYS. However, the first 2th order frequency calculated by JTG D60-2015 [23] are 3.184 Hz, 5.531 Hz respectively, giving a respective discrepancy of 63.4 % and 127.5 % in comparison to the numerical results from ANSYS, which will lead to a larger positive bending moment at mid-span and make larger negative bending moment at support when the vehicle impact effects are considered. Besides, the first 2th order vibration models of the bridge are vertical vibration, the 3th and 4th order models are transverse vibration. It means vertical stiffness of long-span curved box girder bridge is smaller compared with its transverse stiffness. The torsional vibration is firstly occurred in the 5th order vibration model, which means the bridge has good torsion resistance.

In Fig. 5, the errors between theoretical values and ANSYS are smaller and smaller with the increasing of element numbers, this trend is more obvious for high order frequencies.

3.2. Seismic responses calculation

Rayleigh linear damping is adopted in present work, therefore D’ Alembert vibration differential equation of the bridge structure is given by:

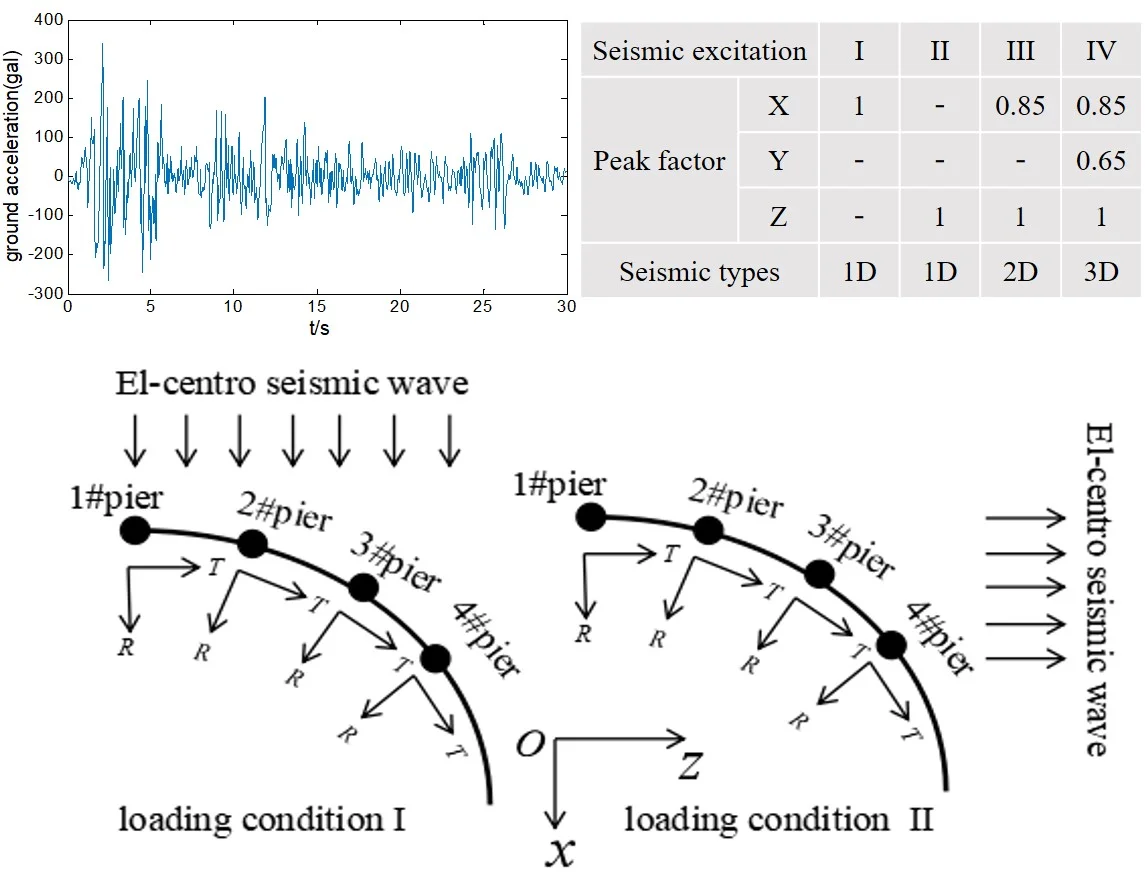
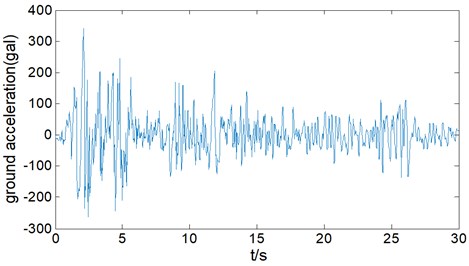
The Newmark-β method [24] is adopted to obtain the seismic response. El-Centro seismic waves (north-south component) is chosen as earthquake excitation in present work as shown in Fig. 6.

Fig. 6El-Centro seismic waves (north-south component)

Generally, 1D horizontal seismic action (longitudinal direction or transverse direction) and 2D horizontal seismic action are mainly considered in bridge seismic resistance. However, vertical seismic action should be also considered for the long-span curved box girder bridge. 4 loading conditions are set in present work as shown in Table 2, peak factor in different directions are set up as 1 (horizontal direction1), 0.85 (horizontal direction 2) and 0.65 (vertical direction).

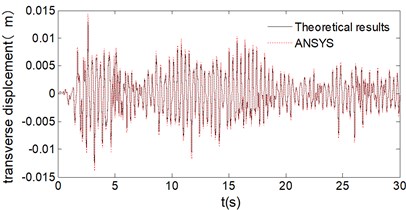
Dynamic responses at 1# pier top under loading condition I are shown as Fig. 7. It can be seen from Fig. 7 that the theoretical results agree well with the finite element results of ANSYS. Based on it, peak dynamic response of all piers under 4 loading conditions are also calculated and the results are shown as Fig. 8, Fig. 9 and Fig. 10.

In Fig. 8(c), Radial acceleration of 1# pier and 4# are 906 gal and 816 gal respectively under transverse horizontal seismic action (loading condition I), while they are 919 gal and 1063 gal respectively under longitudinal horizontal seismic action (working condition II), it indicates that continuous curved box girder bridge is likely to be damaged by transverse girder-falling at both ends under 1D horizontal seismic action. In Fig. 8(a) and Fig. 8(c), radial displacement and acceleration of 4# pier are 18.5 mm and 1063 gal under longitudinal horizontal seismic action, while they are 28.9 mm and 1640 gal under 2D horizontal loading(working condition III), the increasing rates are 56.2 % and 54.3 %, which means peak dynamic response under 2D coupling horizontal seismic action is greater than that under 1D horizontal seismic action. In addition to the 1D horizontal seismic action (transverse or longitudinal direction) during bridge seismic design, an adverse effect of 2D coupling horizontal seismic action should also be considered. Furthermore, peak dynamic response of the curved box girder bridge under 3D seismic action (working condition IV) is almost the same as that under 2D horizontal seismic action, which indicates that vertical seismic action isn’t coupled with horizontal seismic action.

Fig. 7Dynamic response of 1# pier

a) Displacement

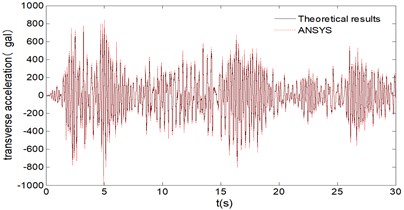
b) Acceleration

Fig. 8Dynamic responses under different loading conditions

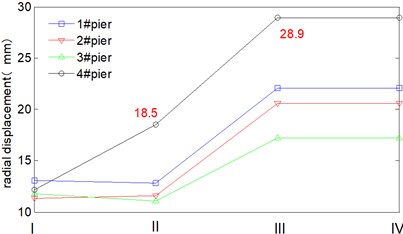
a) Radial displacement

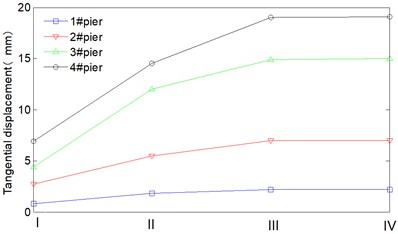
b) Tangential displacement

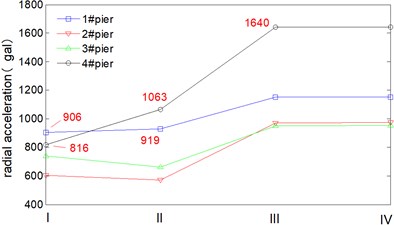
c) Radial acceleration

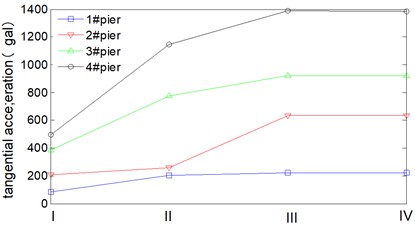
d) Tangential acceleration

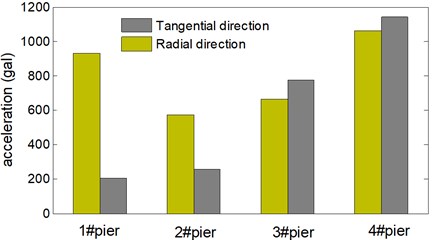
In Fig. 9, radial dynamic responses of all piers are greater than tangential dynamic responses under transverse horizontal seismic action. In Fig. 10, radial dynamic responses of 1# and 2# pier are also greater than tangential dynamic responses under longitudinal seismic action, whilst for 3# pier and 4# pier, their radial dynamic responses are basically equal to their tangential dynamic responses, it indicates that the continuous curved box girder bridge mainly vibrates along transverse direction together with in-plane rotation around 3# pier and 4# pier.

Seismic wave direction of loading condition I and II are shown as Fig. 11, $R$ and $T$ represents the radial direction and tangential direction respectively. Flow cylindrical coordinate system is adopted in the present work, therefore seismic wave direction of loading condition I is exactly coincident with the radial direction of 1# pier, the angle between them is denoted as $\alpha =$ 0°. Seismic wave direction of loading condition II is also exactly coincident with the tangential direction of 1# pier, the angle between them is denoted as $\alpha =$ 90°. There is a certain angle between seismic wave direction and radial direction (or tangential direction) for the rest piers. Under loading condition I, radial responses of each pier are basically equal. Whilst the tangential responses of each pier differ greatly and present obvious spatiality under loading condition II. Besides, the peak displacement doesn’t occur at 1# pier but 4# pier, the radial and tangential displacement are respectively 18.5 mm, 14.5 mm. It indicates that mechanics behavior of the continuous curved box girder bridge is so complicated, and the peak responses may not occur along seismic wave direction.

Fig. 9Dynamic response of the bridge under loading condition I

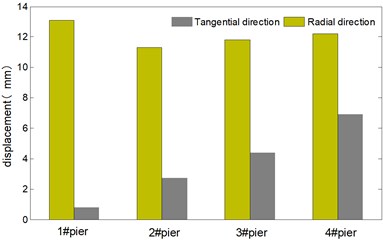
a) Displacement

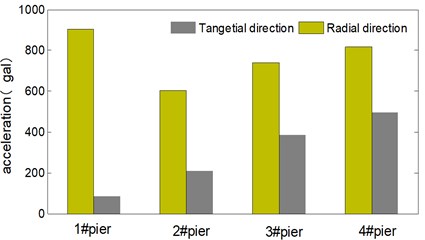
b) Acceleration

Fig. 10Dynamic responses of the bridge under loading condition II

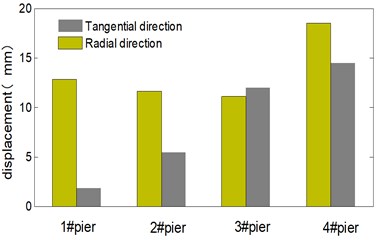
a) Displacement

b) Acceleration

Fig. 11Seismic wave direction of loading condition I and II

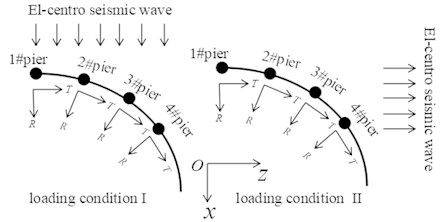
Seismic waves at any direction in the horizontal plane can be decomposed along $x$ and $z$ direction, so there is certainly a critical angle that make the curved box girder bridge reach its peak displacement responses. In order to investigate the critical angle of seismic wave and acquire the peak dynamic response in the range of 0° to 180°, $\mathrm{\Delta }\alpha =$ 5° is set as the increment in present work.

The critical angle of seismic wave is shown as Fig. 12, the peak displacement response of all piers roughly change in sine wave form in the range of 0° to 180°. Both the radial and tangential peak displacements appeared for all the 4 piers as the seismic wave angle reached at 50° and 70°. The radial peak displacements are 16.8 mm, 15.7 mm, 13.2 mm, 22.1 mm respectively, and the tangential peak displacements are 1.9 mm, 5.7 mm, 12.5 mm, 15.5 mm respectively.

Fig. 12Critical angle of seismic wave

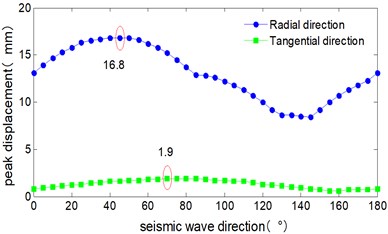
a) 1# pier

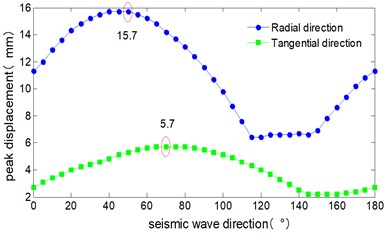
b) 2# pier

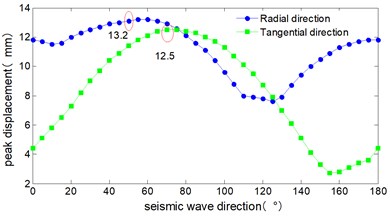
c) 3# pier

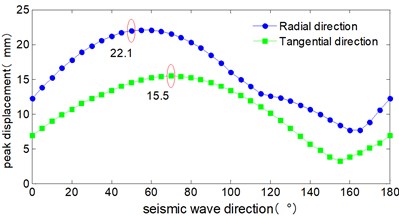
d) 4# pier