Anti-overturning stability coefficient of curved girder bridges considering seismic action

2.1. Calculation formula of anti-overturning stability of curved girder bridge under static force

Specifications for Highway Bridges [20, 21] stipulates the lateral stability and adopts monolithic section of the simply-supported beams and continuous beams to check the anti-overturning according to Eq. (1):

where ${\gamma }_{qf}$ is the anti-overturning stability coefficient, $S_{bk}$ is the effect design value to make the superstructure stable, $S_{sk}$ is the effect design value of capsizing and instability of superstructure, $l_i$ is the vertical spacing between ineffective bearings and overturning axis at the $i$th pier, $R_{Gki}$ is the bearing reaction of the failed bearing at the $i$th pier under permanent action, which is calculated by the effective bearing system of all bearings, $R_{Qki}$ is the bearing reaction of the failed bearing at the $i$th pier under variable action, which is calculated by the effective bearing system of all bearings and valued by combination of standard values, and the value of vehicle load (including impact effect) should be valued according to the most adverse load distribution.

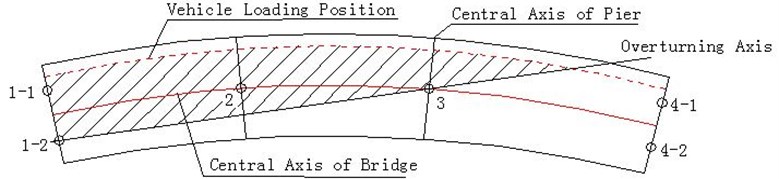
The overturning axis of curved girder bridge is shown in Fig. 1. The determination of the safety coefficient of the bridge anti-overturning is given in literature [21]:

where, $\mathrm{\Omega }$ is the acreage enclosed by the overturning axis and lateral loading lane, and $e$ is the maximum vertical distance between the loading lane and the overturning axis.

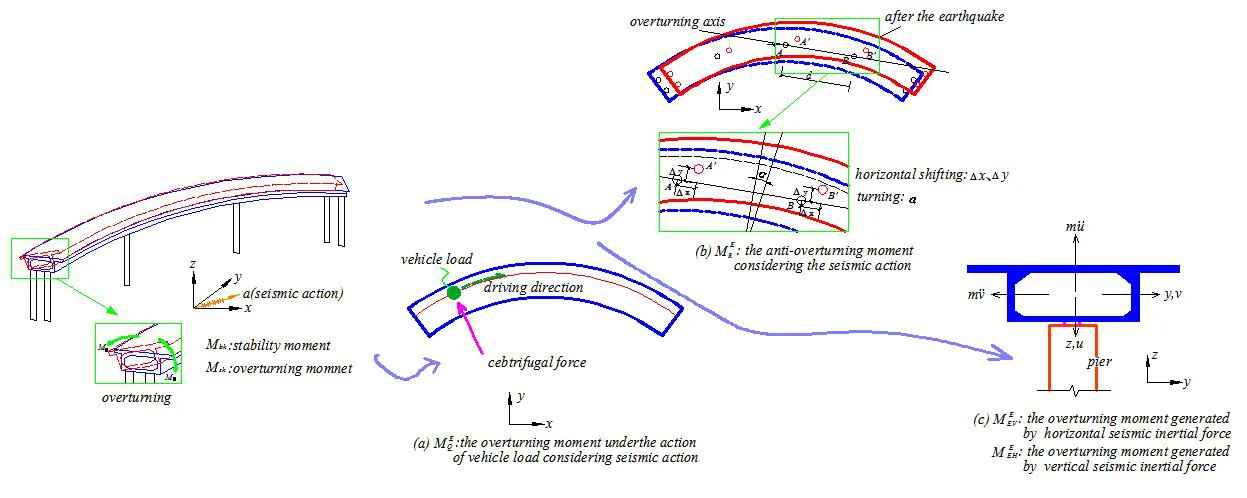
Fig. 1Schematic diagram of curved girder bridge overturning

For curved girder bridges, the paper holds that due to the centrifugal force component of vehicle load, the overturning moment increases, and the anti-overturning safety coefficient decreases accordingly. Therefore, the formula for calculating the anti-overturning safety coefficient of curved girder bridges under static load considering the influence of vehicle centrifugal force is given as below:

where $c=v^2/127R$ is the centrifugal force coefficient, $R$ is the radius of curve, $e_h$ is the distance between the center of gravity of the vehicle and the overturning axis, taking the height 1.2 m above from the bridge deck to the overturning axle, and $s$ is the loading arc length.

2.2. Influence of centrifugal force on anti-overturning stability coefficient of curved girder bridges under static force

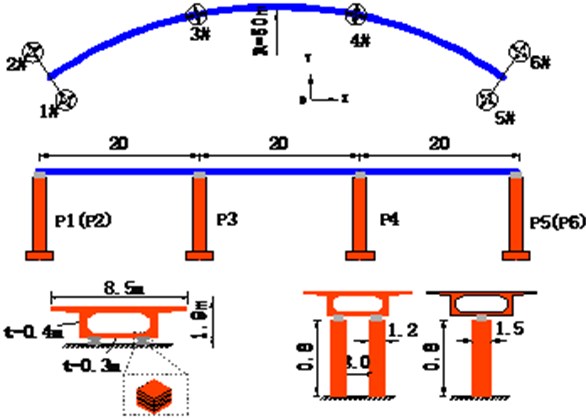
The overall layout of the curved girder bridge and the section size of the main components are shown in Fig. 2. The curve radius of the bridge is 50 m and the span 20 m; The superstructure is single-box and single-cell box girder made of C50 concrete. The main girder is 8.5 m wide and 1.9 m high; both sides of the bridge substructure are designed with double column piers, while the center of the substructure with single column piers of C40 concrete, and piers are 8 m high, both ends of pier 1.2 m in diameter, the middle pier 1.5 m in diameter, the whole bridge adopts the laminated rubber bearings, vertical stiffness of the bearing considered to be with infinite stiffness, and the lateral stiffness is 3000 kN/m.

The software package SAP2000 is used to build the finite element model of the curved girder bridge, where the girder adopts shell elements simulation, the pier adopts stretch beam element simulation, the bearing adopts linear link elements simulation, and the pier foundation adopts the method of consolidation regardless of the pile-soil interaction to the structure.

Fig. 2Overall layout and section of curved girder bridge (in m)

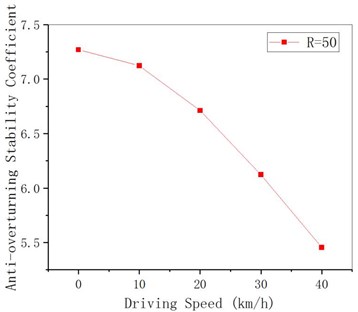
The overturning axis of the bridge is the connecting line of the middle two pier bearings. In combination with the limit requirements of vehicle driving speed in highway route design specification, it is assumed that the speed is 0 km/h (ignoring centrifugal force), 10 km/h, 20 km/h, 30 km/h and 40 km/h. Since the driving speed of the vehicle does not affect anti-overturning moment, the calculated results are all 15860 KN.m. As can be seen from Fig. 3 and Fig. 4, with the growth of vehicle driving speed, the overturning moment changes from 2,181 KN.m when centrifugal force is not considered to 2,907 KN.m when the speed is 40 km/h, and then the anti-overturning stability coefficient decreases from 7.3 to 5.4, with a variation range of 33 % and 26 %, respectively. The results show that it is not safe to calculate the anti-overturning stability coefficient when ignoring the influence of the centrifugal force in the current standard, and the relationship between the anti-overturning stability coefficient and the driving speed can be approximately linear.

Fig. 3Overturning moment of curved girder under different driving speeds

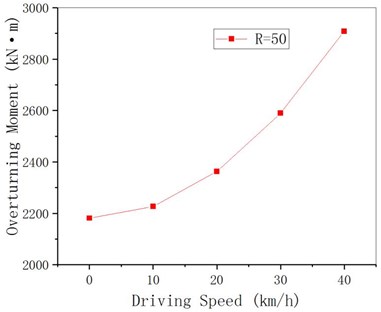
Fig. 4Anti-overturning stability coefficient of curved girder under different driving speeds

3.1. Overturning moment caused by seismic inertial force

Under horizontal seismic action, the inertia forces of the curved girder and vehicle increase the overturning moment of the curved girder bridge, and the overturning moment $M_{EH}^E$ caused by the horizontal seismic inertia forces of curved girder and vehicle on the overturning axis can be expressed as:

where $m_i$ is the mass of girder and each mass point of vehicles (for vehicles, combination coefficient can be valued according to actual situation), $a_{txi}$ is the horizontal acceleration response of the $i$th mass point along the vertical direction of overturning axis to the ground, $a_{txg}$ is the horizontal seismic acceleration of the ground along the vertical direction of overturning axis, $h_i$ is the height of center of mass of the $i$th mass point from the overturning axis (i.e., the height from center of mass to bearing).

Due to the mass of the outer edge of curved girder is larger, the vertical acceleration produces the overturning moment to make the curved girder flip outward. Due to near-field earthquake is close to the zone of fracture, the vertical seismic acceleration attenuation is reduced [23-25], overturning moment caused by the vertical seismic acceleration effect should not be neglected; for near-field earthquake, the influence of the inertia force of vertical vibration on the anti-overturning stability should be considered.

The overturning moment $M_{EV}^E$ caused by the vertical seismic inertial force of curved beam and vehicle on the overturning axis can be expressed as:

where $m_i$ is the mass of each mass point of girder and the vehicle (for vehicles, combination coefficient can be valued according to actual situation), $a_{tyi}$ is the vertical acceleration response of the $i$th mass point relative to the ground, $a_{tyg}$ is the vertical seismic acceleration of the ground, and $e_i$ is the horizontal distance between center of mass of the $i$th mass point and the overturning axis.

3.2. Influence of relative displacement of pier beam on overturning moment and stabilizing moment

Under the horizontal seismic action, translation and turn relative to the pier occur in the curved girder. Translation includes vertical movement along $x$ direction and horizontal movement along $y$direction. With the position change during the curved girder movement, the bearing reaction force under dead load and variant load of bridge changes accordingly, while the overturning axis stays unchanged. The stability moment caused by the dead load, and the overturning moment caused by the variant load change. The larger the displacement is away from the overturning axis, the more unfavorable it is to the anti-overturning of the structure. Therefore, the stability moment considering the horizontal seismic action can be written as:

The overturning moment caused by the vehicle gravity considering influence of horizontal seismic action is:

where $R_{Gki}^E$ is the bearing reaction force of the failure bearing at the $i$th pier after the position of the curved girder changes considering the horizontal seismic action under the dead load, to be calculated according to the effective bearing system of all bearings, ${\mathrm{\Omega }}_E$ is the acreage enclosed by the overturning axis and lateral loading lane after position change of curved girder under horizontal seismic action, $s_E$ is the loading arc length after position change of curved girder under horizontal seismic action, and $e_E$ is the maximum vertical distance between loading lane and overturning axis after position change of curved girder under horizontal seismic action.

Therefore, the anti-overturning stability formula of curved girder bridge under horizontal seismic action is obtained as:

Actually, the seismic action is a dynamic process varying with time, and Eq. (9) is also time-history. When calculating ${\gamma }_{qf}^E$ the minimum value on the time history should be valued.

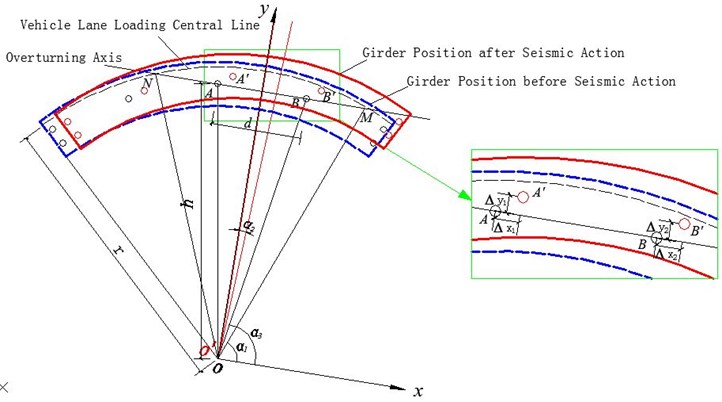
The plane coordinate system in Fig. 5 is established by taking the center point of the curved beam as the origin of coordinates and the direction parallel to the overturning axis as $x$ axial direction. $A$ and $B$ are two points corresponding to bearing centers on overturning axis of curved beam before horizontal movement. It is assumed that under seismic action, the curved girder will have a planar motion as shown in Fig. 5, where $A\mathrm{\text{'}}$ and $B\mathrm{\text{'}}$ are two points after $A$ and $B$ move through the planar motion, $\mathrm{\Delta }{x}_1$ and $\mathrm{\Delta }{y}_1$ are displacements of point $A$ along $x$ and $y$directions of the movement, $\mathrm{\Delta }{x}_2$and $\mathrm{\Delta }{y}_2$ are displacements of point $B$ along $x$ and $y$directions of the movement. The distance between $A$ and $B$ is d, the distance between original point and the two points are both $h$, let the distance between the original point and the center line of loading lane be $r$, the overturning axis and the center line of loading lane intersect at point $M$ and $N$, the angle between $OM$ and $x$ axis is ${\alpha }_1$, and the angle between $OB$ and $x$ axis is ${\alpha }_3$.

Fig. 5Position change of curved beam during horizontal seismic action

Based on the above assumptions, the motion of Fig. 5 can be decomposed into: the curved girder moves along $x$ and $y$ directions first with certain displacements of $e_x$ and $e_y$ by translational motion, and then rotates along the center of the curved girder by a certain angle ${\alpha }_2$. Assume on the curved girder, points $A$ and $B$ move respectively to position $A\text{'}\text{'}$ and $B\text{'}\text{'}$ by translational motion, curved girder center point $O$ to point $O\mathrm{\text{'}}$, curved girder rotates around point $O\mathrm{\text{'}}$ again, point $A$ and $B$, respectively, finally move to point $A\mathrm{\text{'}}$ and $B\mathrm{\text{'}}$. Take the relative displacement of the pier and girder as the premise, the curved girder overturning axis has not changed in the process of horizontal movement, the intersection point of lane loading center line and overturning axis are marked as $M\mathrm{\text{'}}$ and $N\mathrm{\text{'}}$ as shown in Fig. 6.

From the geometric relationship in Fig. 6, it can be seen that: ${\alpha }_2=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}(\mathrm{\Delta }{y}_1-\mathrm{\Delta }{y}_2)/d$, and from Fig. 6, it can be seen that under the rotation angle ${\alpha }_2$, $A\mathrm{\text{'}}\mathrm{\text{'}}$ moves a displacement $l_y$ in $y$ direction to $A\mathrm{\text{'}}$, a displacement of $\mathrm{\Delta }{y}_1$ is made from $A$ to $A\mathrm{\text{'}}$ in $y$ direction:

Obtain $l_y$ to get $e_y$.

Fig. 6Schematic diagram of position change of curved beam lane loading line during horizontal seismic action

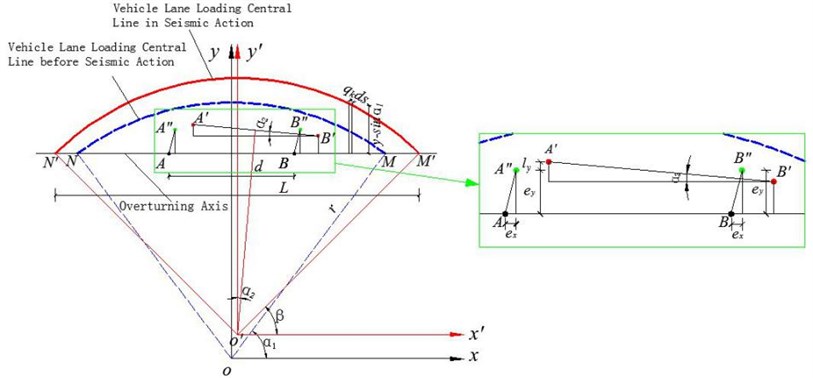
Fig. 7Schematic diagram of rotational displacement change of curved bridge during horizontal seismic action

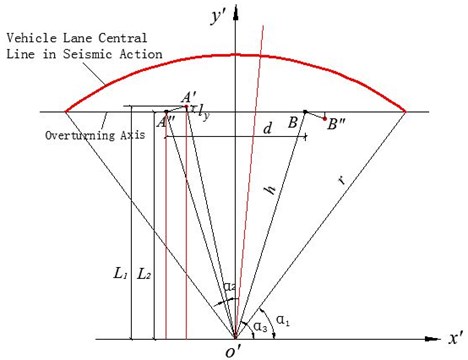
For a curved girder, whether it is first shifted and then rotated, or first rotated and then shifted, the value $l_y$ derived from the rotation of the curved beam stays the same. And it can be seen from Fig. 7, $l_y=L_1-L_2$, $OA=OA\text{'}\text{'}=h$, $L_1=h\cdot \mathrm{s}\mathrm{i}\mathrm{n}({\alpha }_2+{\alpha }_3)$, $L_2=h\cdot \mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_3$, then:

Substitute Eq. (11) into Eq. (10) we obtain:

In Fig. 6, the point on the lane loading center line in the earthquake process in $xoy$ coordinate system satisfies $(x-e_x{)}^2+(y-e_y{)}^2=r^2$, the coordinate value of point $M\mathrm{\text{'}}$ is the same as that on $y$ axis of point $M$, the coordinate of point $M\mathrm{\text{'}}$ obtained is $\left(e_x+\sqrt{r^2-(r\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_1-e_y{)}^2,}r\mathrm{s}\mathrm{i}\mathrm{n}{\alpha }_1\right)$, and the coordinate of $O\mathrm{\text{'}}$ in the $xoy$ coordinate system is ($e_x$, $e_y$), then:

In the $x\mathrm{\text{'}}o\mathrm{\text{'}}y\mathrm{\text{'}}$ coordinate system, the overturning moment $M_q$ caused by the uniformly distributed load on the driveway is calculated as below:

The arc length of the loading line $s_E=\beta r$, therefore, $(q_k\beta r+p_k)$ is the weight of the vehicle load, and the overturning moment provided by the vehicle gravity considering horizontal seismic action is:

where ${\mathrm{\Omega }}_E=r^2(2\mathrm{c}\mathrm{o}\mathrm{s}\beta +2\beta \mathrm{s}\mathrm{i}\mathrm{n}\beta -\pi \mathrm{s}\mathrm{i}\mathrm{n}\beta )$, $e$ is the maximum value of the vertical distance between the loading lane and the overturning axis before the earthquake, $e_y$ and $\beta$ can be obtained from Eq. (12) and Eq. (13), respectively.

4.1. Radius of curvature

Assuming that other structural parameters remain unchanged and the radius of curvature is changed, the anti-overturning stability of curved girder bridge under static and seismic action is analyzed. It can be seen from Figs. 9-11 that: (1) the stability moment under seismic action is slightly lower than that without considering the seismic action, which is consistent with the change law of curved girder radius with and without considering the seismic action. With the increase of curvature radius, it first decreases sharply, then slowly decreases and then slowly increases. (2) considering and not considering the impact of the earthquake overturning moment with the increase of the radius of curvature first sharply reduced, then slowly reduced, and then slowly increased; For girder bridges with a small curvature radius, the overturning moment considering the seismic action is obviously larger than that without considering the earthquake. (3) considering and not considering the seismic action, the anti-overturning stability coefficient is consistent with the change law of the curvature radius.

Fig. 9MRE changes with radius of curvature

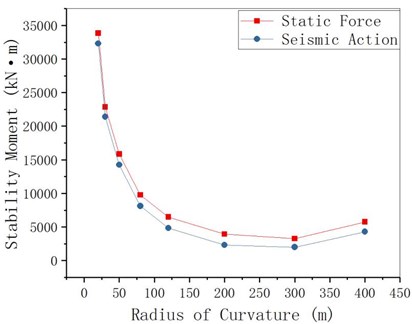
Fig. 10MEE changes with radius of curvature

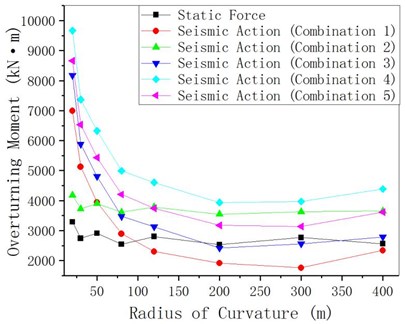
Fig. 11γqfE changes with radius of curvature

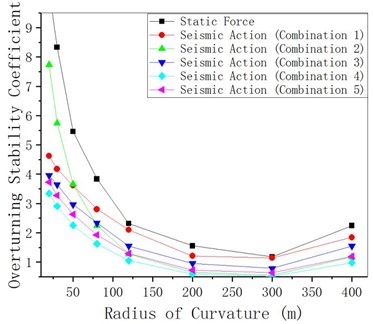
With the increase of the curvature radius, the anti-overturning stability coefficient first decreases sharply, then slowly decreases and then slowly increases. The inflection point is at the location with the curvature radius of 200 m-300 m. The anti-overturning stability coefficient of combinations under different load combinations varies, and the anti-overturning stability coefficient that considers the earthquake effect is smaller than the anti-overturning stability coefficient that does not consider the earthquake effect. The smaller the radius of curvature is, the greater the difference will be. Take combination 1 as an example, the difference is 100 % for $R=$ 20 m and 30 % for $R=$ 200 m.

4.2. Bridge deck width

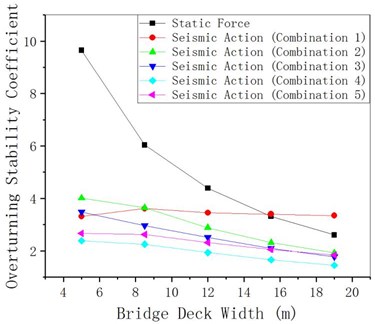
Assuming that structural parameters except the width of bridge deck remain unchanged the anti-overturning stability of curved girder bridges under static and seismic actions is analyzed. From Fig. 12 to Fig. 14, it can be seen that both the overturning moment and the stability moment increase with the growth of the bridge deck width, and the overturning moment under seismic action is smaller than the overturning moment under the action of static force. The anti-overturning stability coefficient under seismic action decreases slightly with the growth of the bridge deck width (the change is minor), while the anti-overturning stability coefficient under static action decreases significantly with the growth of the bridge deck width.

Fig. 12MRE changing with bridge deck width

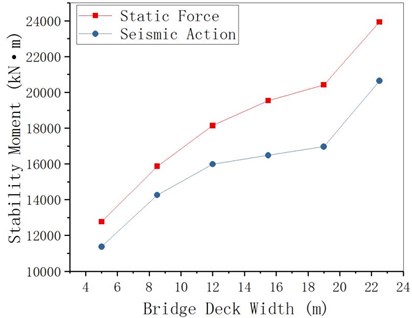
Fig. 13MEE changing with bridge deck width

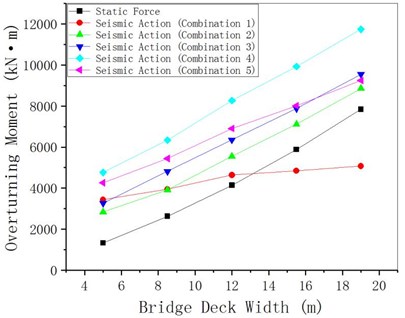
Fig. 14γqfE changing with bridge deck width

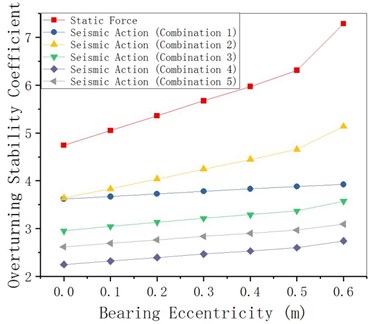
4.3. Bearing eccentricity

The pre-eccentricity of the bearing to the outside of the curve can be set on the middle pier of the curved girder bridge to reduce the torsion of the main girder, improve the in-homogeneity of the force on the inner and outer bearing, and prevent the inner bearing from disengaging. Provided that other parameters remain unchanged, change the bearing eccentricity of the pier bearing in the bearing to analyze the overturning stability of the curved girder bridge under static action and seismic action. From Fig. 15 to Fig. 17, it can be seen that the stability moment under seismic action increases with the bearing eccentricity, the overturning moment changes little with the bearing eccentricity, and the anti-overturning stability coefficient slightly increases with the bearing eccentricity value (changes little).

Fig. 15MRE changes with bearing eccentricity

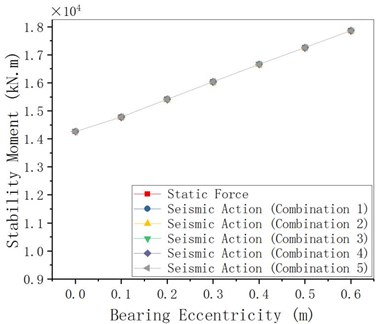
Fig. 16MEE changes with bearing eccentricity

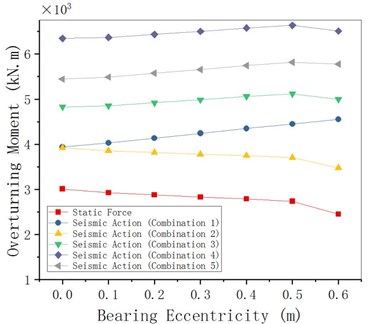
Fig. 17Coefficient changing with bearing eccentricity

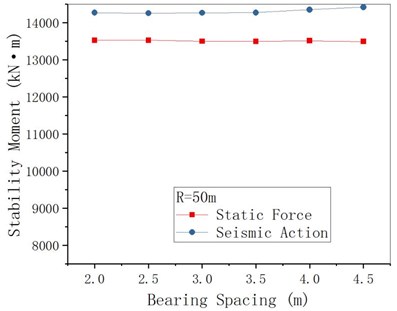
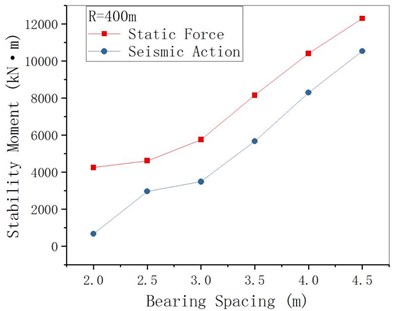
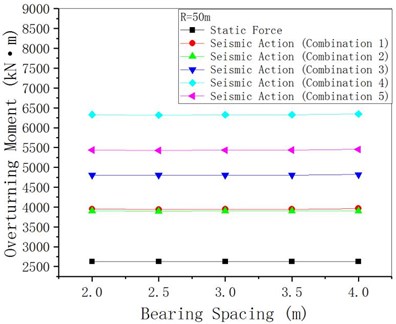
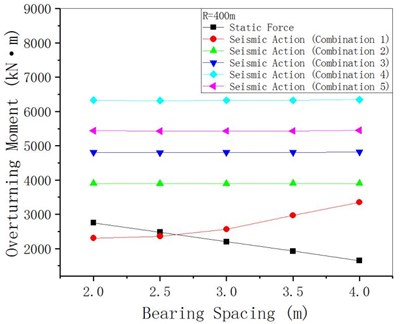
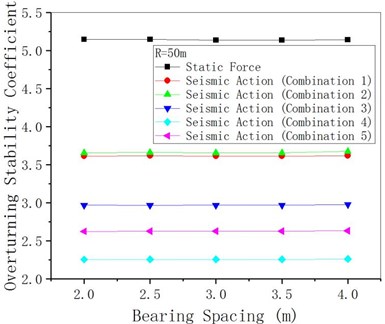
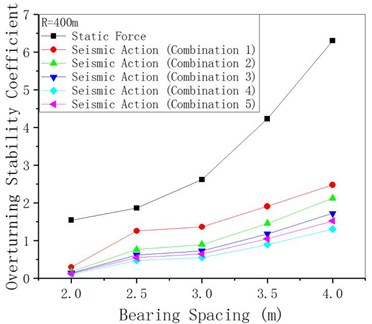
4.4. Bearing spacing

Take $R=$ 50 m and $R=$ 400 m respectively, and change the bearing spacing assuming other structural parameters remain unchanged. The anti-overturning stability analytical results are shown in Figs. 18-20. Because when $R=$ 50 m, the overturning axis of the bridge is the connecting line of two middle pier bearings, the change of abutment distance of joint end (abutments) has little effect on the overturning moment, stability moment and anti-overturning stability coefficient. For $R=$ 400 m when the bridge axis for the league side lateral (outboard bearings at the abutments) bridge pier bearing attachment, under seismic action overturning moment as united end bearing spacing increases, the stability against overturning coefficient end bearing spacing increases, its amplitude is smaller than the static under the action of an increase margin. It shows that for curved girder bridges with a small radius of curvature, the change of the junction bearing spacing has little effect on the stability against overturning, while the increase of the junction bearing spacing in the case of large curvature is helpful to the stability against overturning.

Fig. 18MRE changing with bearing spacing

a)

b)

Fig. 19MEE changing with bearing spacing

a)

b)

Fig. 20γqfE changing with bearing spacing

a)

b)