Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM

Kiryu, Shota; Alisjahbana, Sofia W.; Alisjahbana, Irene; Nagao, Mitsuo; Gan, Buntara S.

doi:10.21595/jve.2018.20431

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2019

Check for updates

Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM

Shota Kiryu¹

Sofia W. Alisjahbana²

Irene Alisjahbana³

Mitsuo Nagao⁴

Buntara S. Gan⁵

¹Department of Architecture, Graduate School of Engineering, Nihon University, Koriyama, Japan

²Faculty of Engineering and Informatics, Bakrie University, Jakarta, Indonesia

³Department of Civil and Environmental Engineering, Master Program Student, Stanford University, California, USA

⁴Department of Mechanical Engineering, College of Engineering, Nihon University, Koriyama, Japan

⁵Department of Architecture, College of Engineering, Nihon University, Koriyama, Japan

Corresponding Author:

Buntara S. Gan

Cite the article Download PDF

Downloads 1799

WoS Core Citations 1

CrossRef Citations 1

Abstract

The exact solution of structural dynamic related problems can be achieved by using the frequency-dependent spectral method. The exact solution is thought to be accurate while reducing the number of degree-of-freedom to resolve the cost and computational drawbacks. This paper investigates the vibrational characteristics of a Levy-type solution of thick plates considering shear deformation based on the two-variable Refined Plate Theory (RPT). The plates, which are modeled by an isotropic Levy-type rectangular plate, were solved by using the Spectral Element Method (SEM). The SEM for RPT Levy-type in the frequency domain is derived to formulate the free vibration problems of the plates. Transcendental stiffness matrices are well established in vibration, formulated from the exact solutions of the differential equations of the RPT Levy-type plate element. The present spectral element model has four line-type degree-of-freedoms (DOF) on each edge of the Levy-type rectangular plate. Natural frequencies of the plate are computed by means of the Wittrick-Williams algorithm. Numerical comparisons are given to show the effectiveness, efficiency, and accuracy of the SEM by using one element. Unlike the FEM, the SEM gives exact solutions of the natural frequencies of plates without element discretization procedures.

1. Introduction

Plates are broadly used in engineering applications due to their valuable features, such as the high strength and stiffness to the weight ratios. Thus, the understanding of the free vibration of plates is indispensable to the engineers across disciplines [1-4]. A reliable and accurate free vibration analysis of plates is required to get safe and reliable designs.

Based on the theory of plates, the effects of shear deformation, particularly in thick plates, are not negligible. Even for thin plates that vibrate in high modes, the effects also need to be considered in the analysis. The Classical Plate Theory (CPT) does not consider the shear effects in the formulations. Hence, some plate theories have been developed to take the effects of shear deformation into the analyses of plates. Reissner [5], Mindlin [6] and Wang [7] developed theory of plates to consider the effect of shear based on the displacement functions assuming constant transverse shear stress through the thickness of the plates. A correction factor is needed to approximate the real shear stress in the plates. Librescu [8], Donnell [9] and Levinson [10] made necessary modifications to the classical plate theory to consider the effects of shear deformation in plates. There are many higher-order theories of plates proposed which are available in the literature. One such example is the two-variable Refined Plate Theory (RPT) [11] which uses two constituents for representing transversal displacement consisting of bending and shear displacements. It is worth noting that the RPT does not use a shear correction factor.

Finite Element Method (FEM) is one of the major and common computational methods available in many fields of science and engineering. The vibration modes of a plate vary depending on the vibration frequencies and its wavelengths. To obtain a sufficiently accurate dynamic response, all necessary high-frequency wave modes have to be considered in the analysis. The size of meshes must be sufficiently small to be used in the modeling. Because the conventional FEM is formulated based on the frequency of independent polynomial shape functions, thus the FEM cannot accommodate all essential high-frequency wave modes without fine discretization. Hence, the FEM solution becomes less accurate, particularly at high frequencies, where the frequencies are related with short wavelengths.

To improve the accuracy of the solution is by using the shape functions, which depend on the natural frequency of the plate. Hence, the shape functions depend on the frequency which are known as the dynamic shape functions. The dynamic shape functions can be considered as necessary in high-frequency wave modes, exceptionally highly accurate solutions can be obtained, and it is not necessary to refine the meshes. This sophisticated concept has directed to the so-called Dynamic Stiffness Method (DSM) [12, 13]. Because the dynamic shape functions are formulated by using exact dynamic stiffness matrix, they treat the mass in a structure member implicitly. Therefore, a regular shape of rigid plate model can be modelled by a single element, irrespective of its length between any two continuous structural or material discontinuities, to obtain exact solutions. The need to refine a regular part of a structure into multiple fine meshes is not necessary. The size of the problem will significantly be reduced by using the least number of meshes and DOFs. As a result, this will significantly reduce the computational time and cost and improving the accuracy of solution by decreasing the errors of computer round-off. Also, the DSM produces infinite number of Eigen solutions by using the exact dynamic stiffness matrix represented by the least number of DOFs. Alike with the formulation of the conventional finite element stiffness matrices, the stiffness of the exact dynamic matrices can be assembled in a similar way as in the FEM. Therefore, in the DSM, the procedures of elements meshing and assembling are very similar with the way in the FEM.

In Spectral Analysis Method (SAM) [14], the solution to the governing differential equations can be achieved by adding infinite number of wave modes with different frequencies. The scheme is very similar with finding the solutions of continuous Fourier transform. To obtain the time histories of the solutions, the Inverse Fourier transform is applied to the infinite set of spectral components in the frequency domain. Only in the mathematically simple problems, the continuous Fourier transform is feasible. In practice, the Discrete Fourier Transform (DFT) is widely used for discontinuous Fourier transform.

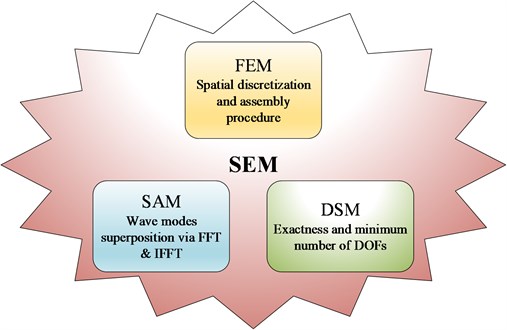
Narayanan and Beskos [15] combined the features of the SAM with those of the DSM by introducing the new concept of the Spectral Element Method (SEM). As illustrated in Fig. 1, the SEM can be considered as the mixture of the main features of the FEM, SAM, and DSM.

Kiryu and Gan [16] have derived and implemented the free vibration problems of isotropic Levy-type plate theory by using SEM. The results show excellent agreement compared with the CPT values reported in the literature.

In this study, the free vibrations of rectangular plates are analyzed. The Levy-type plate theory is based on the first order shear deformation plate theory and the governing equations which can be obtained from both the Hamilton principle and Maxwell equation. The exact natural frequencies of the free vibration plate are investigated. Comparison studies are performed to validate the SEM results. Moreover, the closed-form solutions of isotropic plate based on the RPT [11] is also referred for verification purposes. The effects of plate size aspect ratio on the natural frequencies of the isotropic Levy-type plates are studied and discussed.

Fig. 1A schematic diagram of the spectral element method

2. Levy-type plate

The levy-type plate is defined by a rectangular plate with at least two parallel sides are simply supported and arbitrary at the other edge boundary conditions. The governing equations yield to the coupled partial differential equations which can be decoupled by introducing supplementary functions. The equations that decoupled can be analytically solved by using SEM.

2.1. The equation of motion of a Levy-type plate

Fig. 2 shows a rectangular Levy-type plate with two simply supported sides parallel to the $x$ -axis and the other two arbitrary boundary conditions at the opposite parallel sides to the $y$ -axis.

Fig. 2Levy-type rectangular plate in the FEM scheme

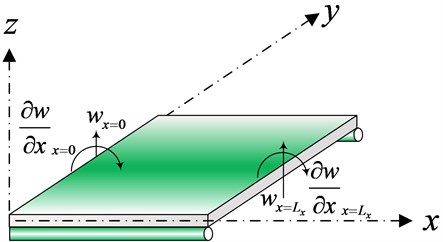
The Levy-type plate has the size of $L_{x}$ and $L_{y}$ in the $x$ and $y$ -directions, respectively. The homogeneous partial differential equations of free vibration considering shear deformation, the transverse displacement $w (x, y, t)$ of the plate is given by the two-variable RPT as:

1

\begin{array}{l} D (\frac{\partial^{4} w_{b}}{\partial x^{4}} + 2 \frac{\partial^{4} w_{b}}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} w_{b}}{\partial y^{4}}) - \frac{ρ h^{3}}{12} (\frac{\partial^{2} {\ddot{w}}_{b}}{\partial x^{2}} + \frac{\partial^{2} {\ddot{w}}_{b}}{\partial y^{2}}) + ρ h ({\ddot{w}}_{b} + {\ddot{w}}_{s}) = 0, \\ \frac{D}{84} (\frac{\partial^{4} w_{s}}{\partial x^{4}} + 2 \frac{\partial^{4} w_{s}}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} w_{s}}{\partial y^{4}}) - \frac{5 E h}{12 (1 + μ)} (\frac{\partial^{2} w_{s}}{\partial x^{2}} + \frac{\partial^{2} w_{s}}{\partial y^{2}}) - \frac{ρ h^{3}}{1008} (\frac{\partial^{2} {\ddot{w}}_{s}}{\partial x^{2}} + \frac{\partial^{2} {\ddot{w}}_{s}}{\partial y^{2}}) \\ + ρ h ({\ddot{w}}_{b} + {\ddot{w}}_{s}) = 0 . \end{array}

The governing equations of the bending moment and transverse shearing force of the plate along the $x$ -direction boundary can be given as:

2

\begin{array}{l} M_{x x b n} (x, y; ω_{n m}) = - D [\frac{\partial^{2} w_{b}}{\partial x^{2}} + μ \frac{\partial^{2} w_{b}}{\partial y^{2}}], \\ Q_{x z b n} (x, y; ω_{n m}) = - D [\frac{\partial^{3} w_{b}}{\partial x^{3}} + (2 - μ) \frac{\partial^{3} w_{b}}{\partial x \partial y^{2}}] + \frac{ρ h^{3}}{12} \frac{\partial {\ddot{w}}_{b}}{\partial x}, \\ M_{x x s n} (x, y; ω_{n m}) = - D [\frac{\partial^{2} w_{s}}{\partial x^{2}} + μ \frac{\partial^{2} w_{s}}{\partial y^{2}}], \\ Q_{x z s n} (x, y; ω_{n m}) = \frac{5 E h}{12 (1 + μ)} \frac{\partial w_{s}}{\partial x} - \frac{D}{84} [\frac{\partial^{3} w_{s}}{\partial x^{3}} + (2 - μ) \frac{\partial^{3} w_{s}}{\partial x \partial y^{2}}] + \frac{ρ h^{3}}{1008} \frac{\partial \ddot{w}}{\partial x}, \end{array}

where, $ρ$ is the mass density, $h$ is the thickness and $D$ is the bending rigidity which is defined by $D = \frac{E h^{3}}{12 (1 - ν^{2})}$ , $ν$ is the Poisson’s ratio and $E$ is the elastic modulus of the plate. The first and second terms in Eq. (1) stand for the shear and bending vertical displacements of the plate.

2.2. Spectral element method (SEM)

Assuming the displacement of the plate in $n$ -domain spectral in the following form:

3

w (x, y, t) = w_{s} (x, y, t) + w_{b} (x, y, t),

where, $w_{s} (x, y, t)$ and $w_{b} (x, y, t)$ are the assumed shear and bending $z$ -direction displacement functions which are expressed by exponential series as follow:

4

\begin{matrix} w_{s} (x, y, t) = \frac{1}{N} \sum_{n = 1}^{N} W_{s n} (x, y; ω_{n}) e^{i ω_{n} t}, w_{b} (x, y, t) = \frac{1}{N} \sum_{n = 1}^{N} W_{b n} (x, y; ω_{n}) e^{i ω_{n} t}, \end{matrix}

with:

5

\begin{matrix} W_{s n} (x, y; ω_{n}) = X_{s n} (x) Y_{s n} (y), W_{b n} (x, y; ω_{n}) = X_{b n} (x) Y_{b n} (y), \end{matrix}

where $W_{s n} (x, y; ω_{n})$ and $W_{b n} (x, y; ω_{n})$ are the spectral components of the $w_{s} (x, y, t)$ and $w_{b} (x, y, t)$ , $N$ is the sampling number and $ω_{n}$ is the $n$ th natural frequency. The spectral component $W_{s n} (x, y; ω_{n})$ and $W_{b n} (x, y; ω_{n})$ are obtained from the multiplications of $X_{s n} (x)$ , $X_{b n} (x)$ and $Y_{s n} (y)$ , $Y_{b n} (y)$ which are the shear and bending parts of the displacement functions in $x$ and $y$ -directions, respectively.

By assuming the $Y_{s n} (y)$ and $Y_{b n} (y)$ solutions in $m$ -domain spectral form as:

6

\begin{matrix} Y_{s n} (y) = \frac{1}{M} \sum_{m = 1}^{M} Y_{s n m} e^{i k_{y n m} y}, Y_{b n} (y) = \frac{1}{M} \sum_{m = 1}^{M} Y_{b n m} e^{i k_{y n m} y}, \end{matrix}

where $k_{y n m}$ is the sampling number and the wavenumbers in $y$ -direction which is given by:

7

k_{y n m} = \frac{m π}{L_{y}}, (m = 1,2, 3, . . .) .

Substitutions of Eq. (6) into Eq. (5), results in:

8

\begin{array}{l} W_{s n m} (x; k_{y n m}, ω_{n m}) = X_{s n} (x; k_{y n m}, ω_{n m}) Y_{s n m}, \\ W_{b n m} (x; k_{y n m}, ω_{n m}) = X_{b n} (x; k_{y n m}, ω_{n m}) Y_{b n m} . \end{array}

After some derivations and substitutions, Eq. (1) can be written as:

9

[D k_{x n m}^{4} + (2 D k_{y n m}^{2} - \frac{ρ h^{3}}{12} ω_{n m}^{2}) k_{x n m}^{2} + D k_{y n m}^{4} - \frac{ρ h^{3}}{12} ω_{n m}^{2} k_{y n m}^{2} - ω_{n m}^{2} ρ h] W_{b n m}

- ω_{n m}^{2} ρ h W_{s n m} = 0,

\begin{matrix} [\frac{D}{84} k_{x n m}^{4} + (\frac{2 D}{84} k_{y n m}^{2} + \frac{5 E h}{12 (1 + μ)} - \frac{ρ h^{3}}{1008} ω_{n m}^{2}) k_{x n m}^{2} + \frac{D}{84} k_{y n m}^{4} \end{matrix}

+ \frac{5 E h}{12 (1 + μ)} k_{y n m}^{2} - \frac{ρ h^{3}}{1008} ω_{n m}^{2} k_{y n m}^{2} - ω_{n m}^{2} ρ h] W_{s n m} - ω_{n m}^{2} ρ h W_{b n m} = 0 .

The general solution of Eq. (9) can be assumed as:

10

\begin{matrix} W_{s n m}^{} (x; k_{y n m}, ω_{n m}) = c_{s n m} e^{- i k_{x n m} x}, W_{b n m}^{} (x; k_{y n m}, ω_{n m}) = c_{b n m} e^{- i k_{x n m} x} . \end{matrix}

Substituting Eq. (10) into the spectral governing equations of Eq. (9), results in:

11

[D k_{x n m}^{4} + (2 D k_{y n m}^{2} - \frac{ρ h^{3}}{12} ω_{n m}^{2}) k_{x n m}^{2} + D k_{y n m}^{4} - \frac{ρ h^{3}}{12} ω_{n m}^{2} k_{y n m}^{2} - ω_{n m}^{2} ρ h]

\cdot [\begin{array}{l} \frac{D}{84} k_{x n m}^{4} + (\frac{2 D}{84} k_{y n m}^{2} + \frac{5 E h}{12 (1 + μ)} - \frac{ρ h^{3}}{1008} ω_{n m}^{2}) k_{x n m}^{2} \\ + \frac{D}{84} k_{y n m}^{4} + \frac{5 E h}{12 (1 + μ)} k_{y n m}^{2} - \frac{ρ h^{3}}{1008} ω_{n m}^{2} k_{y n m}^{2} - ω_{n m}^{2} ρ h \end{array}] - ω_{n m}^{4} ρ h = 0 .

In the matrix form, Eq. (8) can be written as:

12

W_{n m}^{} (x; k_{y n m}, ω_{n m}) = W_{s n m}^{} (x; k_{y n m}, ω_{n m})

+ W_{b n m}^{} (x; k_{y n m}, ω_{n m}) = E_{n m} (x; k_{y n m}, ω_{n m}) c_{n m},

where:

E_{n m} (x; k_{y n m}, ω_{n m}) = [\begin{matrix} e^{- i k_{x n m 1} x} & e^{- i k_{x n m 2} x} & e^{- i k_{x n m 3} x} & e^{- i k_{x n m 4} x} \\ e^{- i k_{x n m 5} x} & e^{- i k_{x n m 6} x} & e^{- i k_{x n m 7} x} & e^{- i k_{x n m 8} x} \end{matrix}],

c_{n m} = {[\begin{array}{l} c_{n m 1} & c_{n m 2} & c_{n m 3} & c_{n m 4} & c_{n m 5} & c_{n m 6} & c_{n m 7} & c_{n m 8} \end{array}]}^{T} .

2.3. Simply supported Levy-type plate

Per definition, the Levy-type plate is defined by a rectangular plate with at least two parallel sides simply supported and arbitrary at the other edges boundary conditions.

The spectral DOF of a simply supported condition of the plate with the boundary conditions at $x =$ 0 and $x = L_{x}$ ; is given by:

13

d_{n} (ω_{n}) \equiv \{\begin{array}{l} W_{1 s n} (y; ω_{n}) \\ Θ_{1 s n} (y; ω_{n}) \\ W_{1 b n} (y; ω_{n}) \\ Θ_{1 b n} (y; ω_{n}) \\ W_{2 s n} (y; ω_{n}) \\ Θ_{2 s n} (y; ω_{n}) \\ W_{2 b n} (y; ω_{n}) \\ Θ_{2 b n} (y; ω_{n}) \end{array}\} = \{\begin{matrix} W_{s n}^{} (0, y; ω_{n}) \\ W_{s n}^{'} (0, y; ω_{n}) \\ W_{b n}^{} (0, y; ω_{n}) \\ W_{b n}^{'} (0, y; ω_{n}) \\ W_{s n}^{} (L_{x}, y; ω_{n}) \\ W_{s n}^{'} (L_{x}, y; ω_{n}) \\ W_{b n}^{} (L_{x}, y; ω_{n}) \\ W_{b n}^{'} (L_{x}, y; ω_{n}) \end{matrix}\} .

Substituting Eq. (12) into Eq. (13), results in:

14

d_{n m} (k_{y n m}, ω_{n}) = Φ_{n m} (k_{y n m}, ω_{n m}) c_{n m} .

In the matrix form, by applying the boundary conditions, the resultant transverse shearing force and bending moment of the plate in Eq. (2) along the $x$ -direction boundary can be given as:

15

f_{n} (ω_{n}) \equiv \{\begin{array}{l} Q_{1 s n m} (k_{y n m}, ω_{n}) \\ M_{1 s n m} (k_{y n m}, ω_{n}) \\ Q_{1 b n m} (k_{y n m}, ω_{n}) \\ M_{1 b n m} (k_{y n m}, ω_{n}) \\ Q_{2 s n m} (k_{y n m}, ω_{n}) \\ M_{2 s n m} (k_{y n m}, ω_{n}) \\ Q_{2 b n m} (k_{y n m}, ω_{n}) \\ M_{2 b n m} (k_{y n m}, ω_{n}) \end{array}\} = \{\begin{matrix} - Q_{x z s n} (0; k_{y n m}, ω_{n}) \\ M_{x x s n} (0; k_{y n m}, ω_{n}) \\ - Q_{x z b n} (0; k_{y n m}, ω_{n}) \\ M_{x x b n} (0; k_{y n m}, ω_{n}) \\ - Q_{x z s n} (L_{x}; k_{y n m}, ω_{n}) \\ M_{x x s n} (L_{x}; k_{y n m}, ω_{n}) \\ - Q_{x z b n} (L_{x}; k_{y n m}, ω_{n}) \\ M_{x x b n} (L_{x}; k_{y n m}, ω_{n}) \end{matrix}\} .

Substituting Eq. (12) into Eq. (2), results in:

16

\begin{array}{l} M_{x x n} (x, y; ω_{n m}) = - D [E_{b n m}^{''} (x) - μ k_{y n m}^{2} E_{b n m} (x)] c_{n m}, \\ Q_{x z n} (x, y; ω_{n m}) = - D [E_{b n m}^{'''} (x) - (2 - μ) k_{y n m}^{2} E_{b n m}^{'} (x)] c_{n m} - ω_{n m}^{2} \frac{ρ h^{3}}{12} E_{b n m}^{'} (x) c_{n m}, \\ M_{x x s n} (x; k_{y n m}, ω_{n m}) = - D [E_{s n m}^{''} (x) - μ k_{y n m}^{2} E_{s n m} (x)] c_{n m}, \\ Q_{x z s n} (x; k_{y n m}, ω_{n m}) = \frac{5 E h}{12 (1 + μ)} E_{s n m}^{'} (x) c_{n m} - \frac{D}{84} [E_{s n m}^{'''} (x) - (2 - μ) k_{y n m}^{2} E_{s n m}^{'} (x)] \\ \cdot c_{n m} - ω_{n m}^{2} \frac{ρ h^{3}}{1008} E_{s n m}^{'} (x) c_{n m} . \end{array}

By substitution of Eq. (15), Eq. (16) can be written as:

17

f_{n m} (k_{y n m}, ω_{n m}) = G_{n m} (k_{y n m}, ω_{n m}) c_{n m} .

The constant vector $c_{n m}$ can be eliminated by taking the inverse of Eq. (14) and substituting into Eq. (17) to obtain the force-displacement relationship of spectral element governing equation for the Levy-type plate element as follow:

18

\begin{array}{l} f_{n m} (k_{y n m}, ω_{n m}) = G_{n m} (k_{y n m}, ω_{n m}) Φ_{n m}^{- 1} (k_{y n m}, ω_{n m}) \cdot d_{n m} (k_{y n m}, ω_{n m}) \\ = S (k_{y n m}, ω_{n m}) d_{n m} (k_{y n m}, ω_{n m}), \end{array}

where, $S (k_{y n m}, ω_{n m}) = G_{n m} (k_{y n m}, ω_{n m}) Φ_{n m}^{- 1} (k_{y n m}, ω_{n m})$ .

The size of the matrix $S (k_{y n m}, ω_{n m})$ is 8×8 which is the function of natural frequency $ω_{n m}$ and wavenumber $k_{y n m}$ .

3. Numerical examples

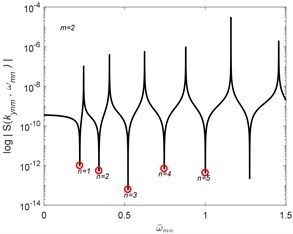
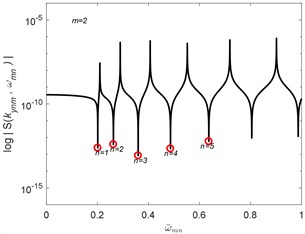
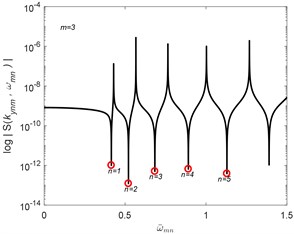
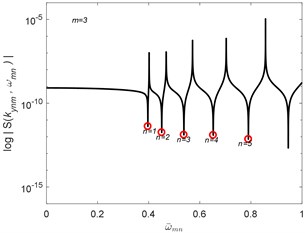
Consider the geometry of two different aspect ratio of width and length of Levy-type plates as shown in Fig. 3. The following material properties of the isotropic plate are used in the calculation: mass density $ρ =$ 1.0; elastic modulus $E =$ 1 and Poisson’s ratio $ν =$ 0.3. The shear modulus is computed from $G = E / 2 (1 + ν)$ . The plates are restrained at both opposite parallel sides by simply supported boundary conditions. Non-dimensional natural frequencies ${\bar{ω}}_{m n} = ω_{m n} h \sqrt{ρ / G}$ of simply-supported SEM plate with $h / L_{y} =$ 0.1 for $n =$ 1 to 5 are computed.

Fig. 3Numerical examples of free vibration of the Levy-type plate using SEM

The natural frequencies of the plates are found by solving the homogeneous equation of the spectral element model of Eq. (18):

19

f_{n m} (k_{y n m}, ω_{n m}) = S (k_{y n m}, ω_{n m}) d_{n m} (k_{y n m}, ω_{n m}) = 0 .

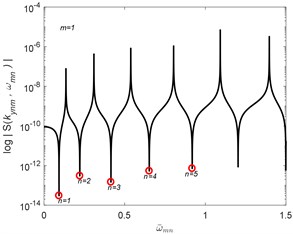
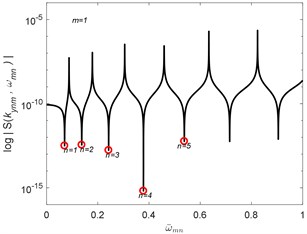
The natural frequencies $ω_{n m}$ , $(m = 1,2, 3 . . .; n = 1,2, 3 . . .)$ are solved by using the condition that the determinant of $S (k_{y n m}, ω_{n m})$ is zero at $ω = ω_{n m}$ , that is:

20

|S (k_{y n m}, ω_{n m})| = 0 .

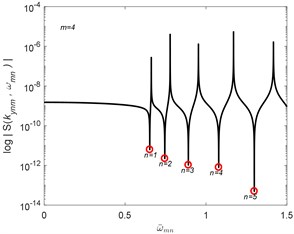
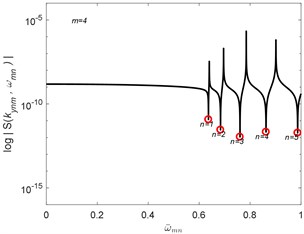
The algorithm of Wittrick-Williams [17] is implemented to compute the natural frequencies of the plates. The results of the normalized natural frequencies of the plates are compared with the RPT solutions [11] as shown in Tables 1, 2 for the square and rectangular Levy-type plates. The present results obtained by using the SEM are found to give accurate and complete natural frequencies values compared with the RPT and exact solutions reported.

Table 1Comparison of normalized natural frequencies ω-mn of Levy-type plates

$m$	$n$	$L_{x} / L_{y} =$ 1.0			$L_{x} / L_{y} = \sqrt{2}$
$m$	$n$	Exact [18]	RPT [11]	Present	Exact [18]	RPT [11]	Present
1	1	0.0932	0.0930	0.0930	0.0704	0.0704	0.0704
1	2	0.2226	0.2220	0.2220	0.1376	0.1373	0.1373
2	1	0.2226	0.2220	0.2220	0.2018	0.2012	0.2012
2	2	0.3421	0.3406	0.3406	0.2634	0.2625	0.2625
1	3	0.4171	0.4151	0.4151	0.2431	0.2424	0.2424
3	1	0.4171	0.4151	0.4151	0.3987	0.3968	0.3968
2	3	0.5239	0.5208	0.5208	0.3612	0.3596	0.3596
3	2	0.5239	0.5208	0.5208	0.4535	0.4511	0.4511
1	4	−	0.6525	0.6525	0.3800	0.3783	0.3783
4	1	−	0.6525	0.6525	−	−	0.6365
3	3	0.6889	0.6840	0.6840	0.5411	0.5378	0.5378
2	4	0.7511	0.7454	0.7454	0.4890	0.4863	0.4863
4	2	0.7511	0.7454	0.7454	−	−	0.6840
3	4	−	0.8908	0.8908	−	−	0.6525
4	3	−	0.8908	0.8908	−	−	0.7604
1	5	0.9268	0.9187	0.9187	0.5411	0.5378	0.5378
5	1	0.9268	0.9187	0.9187	−	−	0.9048
2	5	−	1.0001	1.0001	0.6409	0.6365	0.6365
5	2	−	1.0001	1.0001	−	−	0.9462
4	4	1.0889	1.0785	1.0785	−	−	0.8626
3	5	−	1.1292	1.1292	−	−	0.7901
5	3	−	1.1292	1.1292	−	−	1.1013
4	5	−	−	1.2982	−	−	0.9867
5	4	−	−	1.2982	−	−	1.1040
5	5	−	−	1.4991	−	−	1.2152

Table 2Normalized natural frequencies ω-mn of simply-supported SEM plates

RPT, $L_{x} / L_{y} = 1.0$	RPT, $L_{x} / L_{y} = \sqrt{2}$

4. Conclusions

The present method using SEM featured with the FEM meshing and assembling capabilities was proved to be effective and efficient to solve free vibration problems of two-variable RPT plates. The present SEM gives a good accuracy of the natural frequencies of plates without element discretization procedures necessary. The present SEM has shown that the transcendental stiffness matrices which are well established in free vibration problems can be derived from any theories provided with the governing differential equations of the plate element. The effectiveness of the Wittrick-Williams algorithm also has been found suitable for use in the SEM formulation, as opposed to the approximation method by using the FEM.

References

Alisjahbana S. W., Alisjahbana I., Kiryu S., Gan B. S. Semi analytical solution of a rigid pavement under a moving load on a Kerr foundation model. Journal of Vibroengineering, Vol. 20, Issue 5, 2018, p. 2165-2174.

Publisher
Choi D., Ahn S., Ryu J., Nagao M., Kim Y. Knee acoustic emission characteristics of the healthy and the patients with osteoarthritis using piezoelectric sensor. Sensors and Materials, Vol. 30, Issue 8, 2018, p. 1629-1641.

Publisher
Hong C. C. The GDQ Method of thermal vibration laminated shell with actuating magnetostrictive layers. International Journal of Engineering and Technology Innovation, Vol. 7, Issue 3, 2017, p. 188-200.

Search CrossRef
Kumar R., Vohra R., Gorla M. G. Vibration analysis of thermo elastic micro beam with double porosity structure. International Journal of Engineering and Technology Innovation, Vol. 7, Issue 2, 2017, p. 130-141.

Search CrossRef
Reissner E. The effect of transverse shear deformation on the bending of elastic plates. Journal of Applied Mechanics, Vol. 12, 1945, p. 69-77.

Publisher
Mindlin R. D. Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates. Journal of Applied Mechanics, Vol. 18, 1951, p. 31-38.

Publisher
Wang C. M., Reddy J. N., Lee K. H. Shear Deformable Beams and Plates: Relationships with Classical Solutions. Elsevier Science Ltd., Oxford, 2000.

Search CrossRef
Librescu L. Elastostatics and Kinetics of Anisotropic and Heterogeneous Shell-Type Structures. Noordhoff International, Leyden, The Netherlands, 1975.

Search CrossRef
Donnel L. H. Beams, Plates and Shells. Noordhoff International, Leyden, The Netherlands, 1976.

Search CrossRef
Levinson M. An accurate, simple theory of the statics and dynamics of elastic plates. Mechanics Research Communications, Vol. 7, 1980, p. 343-350.

Publisher
Shimpi R. P., Patel H. G. Free vibrations of plate using two variable refined plate theory. Journal of Sound and Vibration, Vol. 296, 2006, p. 979-999.

Publisher
Banerjee J. R. Dynamic stiffness formulation for structural elements: a general approach. Computers and Structures, Vol. 63, Issue 1, 1977, p. 101-103.

Publisher
Leung A. Y. T. Dynamic Stiffness and Substructures. Springer-Verlag, London, 1993.

Publisher
Doyle J. F. Wave Propagation in Structures: Spectral Analysis Using Fast Discrete Fourier Transforms. Springer, New York, 1997.

Search CrossRef
Narayanan G. V., Beskos D. E. Use of dynamic influence coefficients in forced vibration problems with the aid of fast Fourier transform. Computers and Structures, Vol. 9, Issue 2, 1978, p. 145-150.

Publisher
Kiryu S., Gan B. S. Vibrational analysis of levy-type plates by using SEM. Journal of Advanced Civil and Environmental Engineering, Vol. 1, Issue 1, 2018, p. 18-29.

Publisher
Wittrick W. H., Williams F. W. A general algorithm for computing natural frequencies of elastic structures. Quarterly Journal of Mechanics and Applied Mathematics, Vol. 24, Issue 3, 1971, p. 263-284.

Publisher
Reddy G. V., Phan N. D. Stability and vibration of isotropic, orthotropic and laminated plates according to a higher-order shear deformation theory. Journal of Sound and Vibration, Vol. 98, Issue 2, 1985, p. 157-170.

Publisher

Cited by

A general electroelastic analysis of piezoelectric shells based on levy-type solution and eigenvalue-eigenvector method

Ji Qi | Ran Teng | H. Elhosiny Ali | Mohammad Arefi

(2023)

About this article

Received

17 April 2018

Accepted

01 December 2018

Published

15 May 2019

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/jve.2018.20431

Keywords

free vibration

frequency domain

levy-type plate

two-variable refined plate theory

spectral element method

Acknowledgements

The fund supported this work was granted by Kanda Package Co., Ltd. through the Emergency Operation Room (ER) Honeyrial Panel Assembly Project.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 11 27

Vibrational analysis of orthotropic rectangular plate having combination of circular thickness and parabolic temperature

Neeraj Lather, Ankit Kumar, Madhu Gupta, Pawan Joshi, Amit Sharma

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2019 11 28

Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

Manish Chauhan, Vinayak Ranjan, Prabhakar Sathujoda

Research article

2019 03 15

Free vibrational characteristics determination of plates with various cutouts

M. L. Pavan Kishore, Ch. Rajesh, Ram Komawar

S. Kiryu, S. W. Alisjahbana, I. Alisjahbana, M. Nagao, and B. S. Gan, “Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM,” Journal of Vibroengineering, Vol. 21, No. 3, pp. 726–735, May 2019, https://doi.org/10.21595/jve.2018.20431

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2018.20431
UR  - https://doi.org/10.21595/jve.2018.20431
TI  - Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM
T2  - Journal of Vibroengineering
AU  - Gan, Buntara S.
AU  - Kiryu, Shota
AU  - Alisjahbana, Sofia W.
AU  - Alisjahbana, Irene
AU  - Nagao, Mitsuo
PY  - 2019
DA  - 2019/05/15
PB  - JVE International Ltd.
SP  - 726-735
IS  - 3
VL  - 21
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Gan_2019,
	doi = {10.21595/jve.2018.20431},
	url = {https://doi.org/10.21595/jve.2018.20431},
	year = 2019,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	number = {3},
	pages = {726--735},
	author = {Buntara S. Gan and Shota Kiryu and Sofia W. Alisjahbana and Irene Alisjahbana and Mitsuo Nagao},
	title = {Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using {SEM}},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]B. S. Gan, S. Kiryu, S. W. Alisjahbana, I. Alisjahbana, and M. Nagao, “Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM,” Journal of Vibroengineering, vol. 21, no. 3, pp. 726–735, May 2019, doi: 10.21595/jve.2018.20431.

Copy IEEE

Copied to clipboard!

Gan, Buntara S., Shota Kiryu, Sofia W. Alisjahbana, Irene Alisjahbana, and Mitsuo Nagao. “Free Vibration of a Levy-Type Solution for Plates Based on Two-Variable Refined Plate Theory by Using SEM.” Journal of Vibroengineering 21, no. 3 (May 15, 2019): 726–35. https://doi.org/10.21595/jve.2018.20431.

Copy Chicago

Copied to clipboard!

Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM

Abstract

1. Introduction

2. Levy-type plate

2.1. The equation of motion of a Levy-type plate

2.2. Spectral element method (SEM)

2.3. Simply supported Levy-type plate

3. Numerical examples

4. Conclusions

References

Cited by

About this article

Related Articles