Abstract
The shaking table model test mainly focuses on the study of seismic response law, aseismic performance and seismic damping and isolation effect of bridges with a single or multi-platform shaking table. Basically, the plane principal axis direction is adopted for the seismic input of structural models. Little research effort considering multi-angle seismic input has been reported in the structural model test. In this paper we designed and conducted a small-scale shaking table model test to study the seismic response law of the curved girder bridges with seismic input at different angles, and provided experimental verification for the theoretical method of the most unfavorable angle of seismic input. The experimental results show that the variation trend of component response to variation of the seismic input direction is consistent with that of the numerical analysis, which indicates that the designed device is effective.
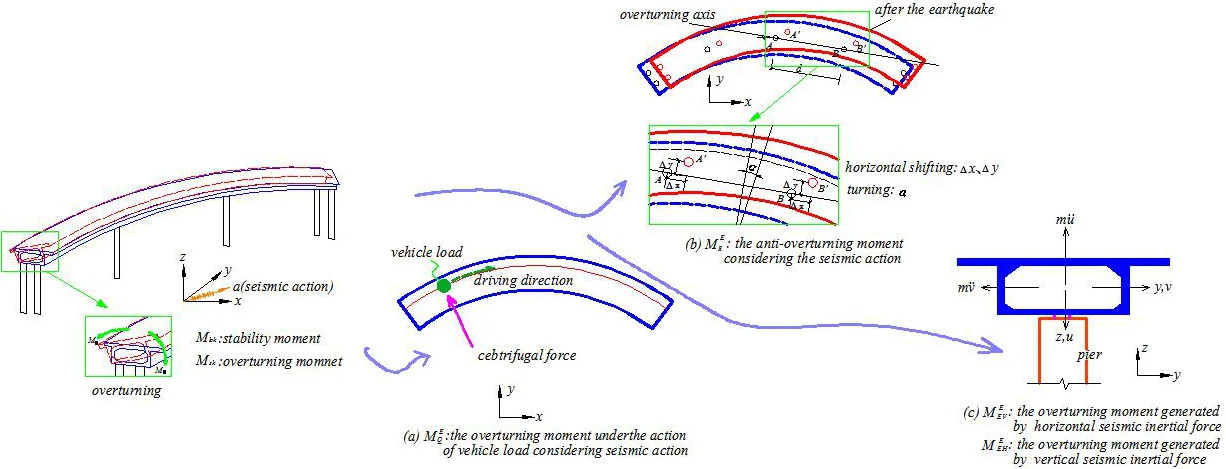
Highlights
- Design and carry out a small vibration table model test to study the seismic response law of seismic input to curved beam bridges under different angles
- Experimental verification of theoretical methods for the most unfavorable input directions
- The calculating equation of anti-overturning stability coefficient under static action is modified
1. Introduction
Shaking table simulation is one of the important means to study the dynamic response of bridge structures. Li Zhongxian and Zhang Yong et al. (2007) [1] studied the collision reaction of seismic isolation and simply supported beam bridge under earthquake using a single-dimensional shaking table. Wang Lei (2010) [2] studied the dynamic response of long-span curved bridge structure under various seismic conditions using a 9-platform shaking table array system. Yan Xiaoyu (2013) [3] studied the seismic response characteristics of long-span bridges under multi-point excitation through multi-platform shaking table array equipment. Yin Junhong et al. (2015) [4] used a one-way excitation shaking table to explore the failure rule of continuous beam bridges with C-shaped, S-shaped and herringbone curves. Liu Yanhui and Tan Ping et al. (2015) [5] used a three-way six-degree-of-freedom shaking table to study the anti-seismic and damping performance of the with high pier isolated continuous beam bridge. Using a single dimensional shaking table, Wen Jianian and Li Hongying et al. (2016) [6] studied the response characteristics and isolation effect of three kinds of isolation bridges with single spherical friction pendulum bearing, double concave friction pendulum bearing and multi-spherical sliding friction bearing. He Lixiang and Ren Weixin et al. (2016) [7] used two shaking tables with three-way six-degree- of-freedom to investigate the impact response of adjacent bridge structures under multi-dimensional multi-point earthquake. Jia Junfeng and Zhao Jianyu et al. (2017) [8] used the shaking table to study the seismic response and 3-D isolation effect of 3-D isolated continuous girder bridges. The sliding phenomenon of plate rubber bearing subjected to earthquake was studied by experiment on a single-dimensional shaking table by Wang Kairui and Xu Xiuli (2017) [9] et al. Xiang Nailiang and Li Jianzhong (2018) [10] carried out a series of research on the aseismic performance of different pier-beam horizontal restraint system by using the large scale model test of multi-function shaking table of Tongji University. Wudi and Dai Longhua, et al. (2018) [11] used a three-way six-degree-of-freedom shaking table to study the seismic reduction and isolation performance of high-speed railway bridges supported by friction pendulum bearings.
Currently, most shaking table model tests focus on the study of seismic response law, aseismic performance, seismic reduction and isolation effect and failure laws of bridges with single or multi-sub-table shaking table. The seismic input of structural models basically adopts plane principal axis direction, while the study of structural model tests with multi-angle seismic input is rarely found. Therefore, this paper designs and conducts a small-scale shaking table model test to study the seismic response rule of curved girder bridge with seismic input at different angles.
2. Modeling
2.1. Model parameters
A typical three-span curved continuous beam bridge is selected as the prototype structure; the concrete mark of main beam and pier column is C40, and the full bridge bearing is plate rubber bearing.
The similarity relation between model structure and prototype structure is deduced by dimensional analysis, and the similarity coefficient is calculated.
2.2. Implementation of multi-angle rotation
Rigid base shall be designed to ensure the reliable connection between the model and the shaking table, enabling the seismic wave to transfer into the structure effectively. The purpose of this experiment is to verify the critical angle of seismic incidence by exploring the seismic response of curved girder bridge with multi-direction input. Since the actuator can only input one-way along the shaking table, the multi-angle seismic input should be realized by rotating the model. Therefore, a rigid base with rotatable function should be devised. The base design and rotation diagram are shown in Fig. 1.
Fig. 1Input in the direction of 45°

3. Shaking table test system
3.1. Seismic simulation drive system
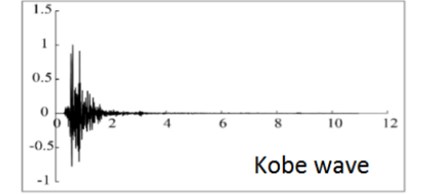
The model test was driven by YJS-HJ-I small shaking table test rig produced by Yantai Xintiandi Test Technology Co., Ltd. In this experiment, Kobe seismic wave and ground motion record were scaled according to the time similarity ratio (original wave: test wave = 1: 0.07303). Meanwhile, adjust the peak value of acceleration to 1.5 g. The time history and response spectrum curves of vibrations of different places selected after scaling are shown in Fig. 2.
The purpose of this experiment is to realize the seismic response of curved bridge with multi-angle input and to obtain the critical angle of seismic incidence. Since the model is symmetrical with horizontal direction of the bridge, the variation range of the ground motion input angle theta can be taken as = 0°-180°, the angle changes every 15°. In Fig. 2, define clockwise rotation of the model as positive.
Fig. 2Time history curve of input seismic wave
3.2. Sensor arrangements
According to the purpose of the test, the bending moment of the pier and the displacement at both ends of the main beam are selected as the engineering demand parameters. In order to accurately measure the actual values of the engineering demand parameters mentioned above, on the local tangential and normal bending moments of the pier section at 1 cm away from the bottom of the pier were pasted with strain gauges respectively to obtain the shear and normal bending moments of the pier. The mid-span and end-point of each span of the main beam and the end of the side pier cover beam are arranged with displacement measuring points.
3.3. Signal testing and data acquisition
In this test, the strain data are collected using a 32-channel DH5923 dynamic signal test and analysis system with sampling frequencies ranging from 10 to 100 k (Hz). The displacement of the model measurement points along the tangential and radial directions should be collected, so a non-contact dynamic displacement measurement system based on Optotrok Certus developed by NDI Corporation is adopted.
4. Test model and analysis
4.1. Performance test of model materials
To compare with the finite element model, the actual elastic modulus of each plexiglass member was tested. The objective of this study is to simulate the structural response under the seismic action, and it is essential to test its dynamic elastic modulus. Test result shows that the dynamic elastic modulus under the dynamic action of 5 mm thin plate is 1.62 GPa, and the dynamic elastic modulus under the diameter of 30 mm 3.11 GPa.
4.2. Structural dynamic response under seismic excitation with different input directions
Fig. 3 indicates that the dynamic response is roughly consistent with the input seismic fluctuation characteristics.
Fig. 3Time history of displacement at left end of main beam and bottom tangential moment of 2# pier under Kobe wave (a= 1.5 g, θ= 0°)
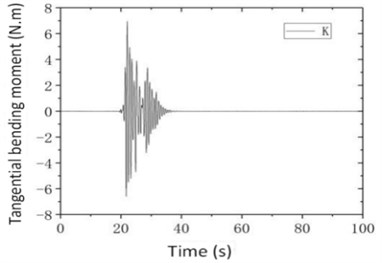
a) 2# pier bottom tangential moment time history
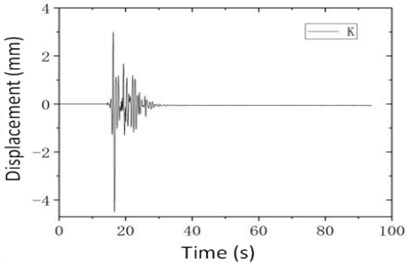
b)-direction displacement time history of the left end of the main beam
4.3. Test results analysis
To verify the coincidence of seismic response and theoretical calculation of curved bridge with multi-angle input, the finite element model of curved bridge was built. The numerical model of the test sample is generated in the large-scale finite element software Sap2000. The elastic beam element is used to simulate the main beam, cover beam and bridge pier, and the linear connection element is used to simulate the rubber, the horizontal stiffness of the support is 7.126 kN/m, and the bottom of the pier is treated by the consolidation method. According to the test results, the responses of the bending moment and the displacement at the end of each pier can be obtained with the change of the seismic input direction. Meanwhile, the time-history analysis is conducted from angle to angle based on the finite element model the experimental and numerical results are compared and shown in Fig. 4. As shown in the graph, the variation trend of bending moment and displacement along with the seismic input direction is basically consistent with the numerical results, which proves the rationality of the design of the experimental model and the accuracy of the finite element model. The critical angle of seismic incidence of the structure in practical engineering can be determined effectively with a high compatibility.
Fig. 4The responses of the bending moment and the displacement at the end of each pier under 1.5 g Kobe wave with the change of vibration excitation direction
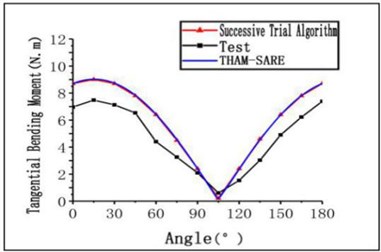
a) The peak value of the moment component response of each pier
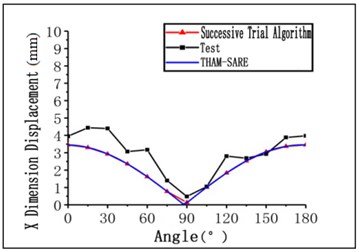
b) The change of peak value of beam end displacement
5. Conclusions
Through the proposed shaking table test of the seismic response of curved girder bridge with multi-angle input and the critical angle of seismic incidence, the finite element model is built. By comparing the numerical simulation with the test results, main conclusions are drawn as follows.
1) This design of the experimental device can realize the seismic excitation of different input directions by rotating model base and provide the technical support for the research of the critical angle of seismic incidence of the structure.
2) Basically, the numerical simulation of the variation of the bending moment and displacement peak value with the seismic input direction agrees with the experimental results, indicating that the device designed in this paper is effective.
References
-
Li Z. X., Zhang Y., Yue F. Q. Shaking table test on pounding response of simply supported isolated bridges under earthquake excitation. Earthquake Engineering and Engineering Vibration, Vol. 27, Issue 2, 2007, p. 152-157.
-
Wang L. Seismic Response Analysis of Long-Span Rigid-Frame Bridge and the Shaking Table Model Test. Beijing Jiaotong University, 2010.
-
Yan X. Y. Shaking Tables Test on Seismic Responses of Long-Span Reinforced Concrete Bridges under Multi-Support Excitations. Tianjin University, 2013.
-
Yin J. H. Shaking Table Test of Irregular Bridge and Study on Impact Response Spectrum. Xi’an University of Architecture and Technology, 2015.
-
Liu Y. H., Tan P., Zhou F. L., et al. Shaking table test for seismic girder bridge simulation of continuous isolation with high piers. China Journal of Highway and Transport, Vol. 28, Issue 2, 2015, p. 61-94.
-
Wen J. N., Li H. Y., Han Q., et al. Shaking table tests of bridge model with sliding friction isolation bearings. Earthquake Engineering and Engineering Vibration, Vol. 36, Issue 2, 2016, p. 102-110.
-
He L. X., Ren W. X., Wang N. B., et al. Experimental study on seismic pounding response of bridge structures subjected to spatially varying ground motions by shake table test. Earthquake Engineering and Engineering Vibration, Vol. 36, Issue 1, 2016, p. 24-34.
-
Jia J. F., Zhao J. Y., Guo Y., et al. Shaking table tests on seismic simulation of three-dimensional isolated continuous girder bridges. China Journal of Highway and Transport, Vol. 30, Issue 12, 2017, p. 290-298.
-
Wang K. R., Xu X. L., Li X. H., et al. A study of the concrete continuous girder bridge shaking table test considering the sliding of laminated rubber bearings. Journal of Vibration and Shock, Vol. 36, Issue 12, 2017, p. 68-74.
-
Xiang N. L., Li J. Z. Shaking table tests of a short to medium-span girder bridge considering the sliding of laminated-rubber bearings. China Civil Engineering Journal, Vol. 51, Issue 7, 2018, p. 104-111.
-
Wu D., Dai L. H., Yan X. Q., et al. Simulated seismic shaking table test of high-speed railway isolated bridges. Railway Construction, Vol. 58, Issue 4, 2018, p. 29-33.
About this article
This work was financially supported by The Key R&D Project of Jiangxi Science and Technology Department No. 20192BBH80021, Scientific Project of Education Department of Jiangxi Province GJJ160620, Science and Technology Project of Communications Department of Jiangxi Province 2016C0006.
