Seismic response analysis of single-pylon suspension bridge under random ground motion

1. Introduction

In earthquake engineering, the reasonable description and modeling of the stochastic process of ground motion is an important basis for the analysis of the structural stochastic seismic response. Since Housner [1] first regarded ground motion as a random process in 1947, the research on random ground motion has been extensively and deeply developed. However, for nonlinear stochastic seismic response analysis of structures, the simulation of stochastic earthquake excitation also requires the conversion process from frequency domain to time domain. For this reason, scholars have carried out extensive research on stochastic process simulation. Spectral representation method is widely used due to its perfect theory and simple algorithm [2]-[4], but its computational workload is large, and it often requires the simulation of hundreds or thousands of random variables to meet the required accuracy. In order to reduce the application difficulty of spectral representation, in recent years, Liu et al. [5] proposed the ground motion modeling method of orthogonal random variables based on Priestley evolutionary spectrum theory. This method can use two basic random variables to describe the random process of ground motion, which greatly reduces the difficulty of structural random dynamic response analysis. Firstly, the finite element model of suspension bridge is established according to the actual bridge engineering in Southwest China. The random ground motion is simulated based on the stochastic function method, and the simulated ground motion samples are input into the finite element model. Finally, the bridge pylon bearing and pylon section response are analyzed, so as to promote the practical application of the dimension reduction simulation theory of seismic random excitation.

2. Finite element modeling of suspension bridges

This paper selects the asymmetric long-span single pylon suspension bridge located in Yunnan Province is employed in this research. The main span of the bridge is 780 m, and the rise span ratio of the main cable is 1/11. The main beam adopts a streamlined flat steel box girder with a width of 31.4 m. The pylon beam separation structure is adopted on Chuxiong bank, and the 156 m main pylon near Yuxi bank adopts reinforced concrete portal rigid frame structure. The main pylon beam adopts a rectangular hollow box section. A pile group foundation is used under the main pylon to ensure sufficient stability and strength of the foundation.

Fig. 1Finite element model of the bridge

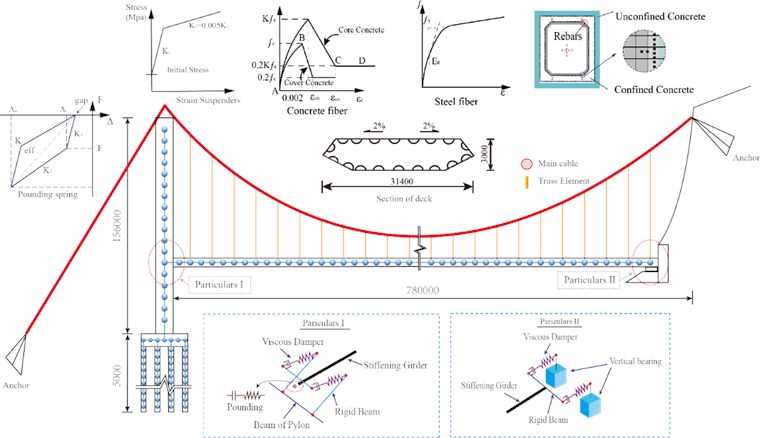
Based on OpenSees nonlinear finite element software, a three-dimensional finite element model is established, as shown in Fig. 1. In which, displacement-based Beam-Column element is used to model girder of suspension bridge. To account for the variable section of the main beam, a smaller element length is selected and the variable section properties are assigned to the two end nodes of the model element. As the main vulnerable component of suspension bridge under earthquake, the Non-linear Beam-column Element based on flexibility method and fiber section is used to simulate the elastic-plastic behavior of bridge pylon under strong ground motion. At the same time, the constrained concrete in the core area is simulated by the concrete material Concrete02 in OpenSees, and the nonlinear characteristics of the unconstrained concrete are reflected by the Kent-Scott-Park constitutive model [6]. The reinforcement material is simulated by Steel02, and the Giuffr-Menegoto-Pinto constitutive model is used to characterize the reinforcement properties [7]. Due to the large-span and flexible characteristics of suspension bridges, the nonlinear effects of main cables and suspension cables (including prestressing effects and stress-stiffening effects) are particularly obvious, and Truss Elements are used for simulation here. The bearing capacity of vertical compression bearing is simulated by using materials of Zero-Length Element and Hardening Elements. The soil- pile interaction (SPI) cannot be ignored in the seismic action analysis of long-span suspension bridges. In this study, the p-y method is used to simulate the SPI, and the Zero-Length Element is used to simulate the p-y nonlinear behavior in the finite element model. Table 1 summarizes the materials and elements used for finite element modeling of each member of the suspension bridge.

3. Finite element modeling of suspension bridges

3.1. Stochastic earthquake dimensionality reduction simulation

According to Priestley’s evolution spectrum representation theory, the random ground motion $X\left(t\right)$ can be approximated by the following finite series [8]:

1

$\widehat{X}\left(t\right)={\sum }_{k=1}^N\sqrt{2S_X\left({\omega }_k,t\right)\mathrm{\Delta }\omega }\left[\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{k}t\right){\alpha }_k+\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_{k}t\right){\beta }_k\right],$

where $\left\{{\alpha }_k,{\beta }_k\right\}$ represents a set of standard orthogonal random variables that satisfy the following conditions [9]:

2

$E\left[{\alpha }_k\right]=E\left[{\beta }_k\right]=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}E\left[{\alpha }_j{\beta }_k\right]=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}E\left[{\alpha }_j{\alpha }_k\right]=E\left[{\beta }_j{\beta }_k\right]={\delta }_{jk}.$

For the construction of orthogonal random variables, first generate representative sample points of random variables $\left\{{\theta }_1,{\theta }_2\right\}\in \left[\mathrm{0,2}\pi \right)$ satisfying uniform distribution and independent of each other, and construct the independent orthogonal random variables as follows:

3

${\widehat{\alpha }}_k=\mathrm{c}\mathrm{a}\mathrm{s}\left(k{\theta }_1\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{\widehat{\beta }}_k=\mathrm{c}\mathrm{a}\mathrm{s}\left(k{\theta }_2\right),\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}k=\mathrm{1,2},\cdots ,N,$

where $cas=\mathrm{s}\mathrm{i}\mathrm{n}(\cdot )+\mathrm{c}\mathrm{o}\mathrm{s}(\cdot )$ is the Hartley function; $\left\{{\widehat{\alpha }}_k,{\widehat{\beta }}_k\right\}$ satisfies the orthogonality condition of Eq. (2), for which the mapping process of $\left\{{\widehat{\alpha }}_k,{\widehat{\beta }}_k\right\}\Rightarrow \left\{{\alpha }_k,{\beta }_k\right\}$ is expanded and the stochastic nonsmooth process $\widehat{X}\left(t\right)$ is generated by Eq. (1). Up to this point, the dimensionality of the random variables has been reduced to 2 dimensions, and the uncertainty characteristics of the earthquake ground motion can be represented by ${\theta }_1$ and ${\theta }_2$.

The seismic intensity of the fortification at the location of the bridge is grade VIII, the site grade is grade II, and the seismic peak acceleration is ${\stackrel{-}{a}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=$ 392 cm/s². For the time-frequency conversion of non-smooth random ground vibrations, the bilateral evolving power spectral density (EPSD) model proposed in the Ref. [10] is used here to generate the EPSD function as follows:

4

$S\left(\omega ,t\right)=A(t{)}^2\frac{{\omega }_e(t{)}^4+4{\omega }_e(t{)}^2{\xi }_e(t{)}^2{\omega }^2}{{\left[{\omega }^2-{\omega }_e(t{)}^2\right]}^2+4{\omega }_e\left(t{)}^2{\xi }_e\right(t{)}^2{\omega }^2}$
$\cdot \frac{{\omega }^4}{{\left[{\omega }^2-{\omega }_f(t{)}^2\right]}^2+4{\omega }_f\left(t{)}^2{\xi }_f\right(t{)}^2{\omega }^2}\cdot S_0\left(t\right),$

where $S_0\left(t\right)$ is the seismic intensity factor and $A\left(t\right)$ is the time modulation function. The values are as follows:

5

$S_0\left(t\right)=\frac{{\stackrel{-}{a}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{{\stackrel{-}{\gamma }}^2\left[\pi {\omega }_e\left(t\right)\left(2{\xi }_e\left(t\right)\right)+\frac{1}{2{\xi }_e\left(t\right)}\right]},$

6

$A\left(t\right)={\left[\frac{t}{c}\mathrm{e}\mathrm{x}\mathrm{p}\left(1-\frac{t}{c}\right)\right]}^d,$

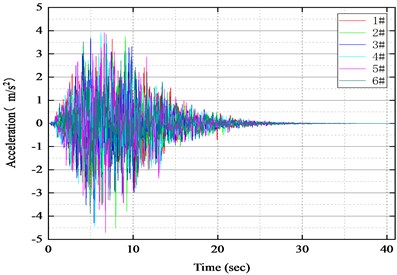
where $T$ is the duration of ground motion, ${\stackrel{-}{a}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{}}$ is the peak acceleration of ground motion. ${\omega }_0$, ${\xi }_0$, $a$ and $b$ are site conditions and design seismic characteristic parameters. In this study, EPSD parameters were selected as: $T=\mathrm{}$20.96 s, $a=\mathrm{}$3, $b=\mathrm{}$0.35, $c=\mathrm{}$6, $d=\mathrm{}$2, $\stackrel{-}{\gamma }=$ 2.75. According to the above conditions, 100 ground motion samples were randomly generated, and 6 representative ground motion samples were selected as shown in Fig. 2, from which the peak value and non-stationary characteristics of ground motion can be seen.

Fig. 2Representative earthquake samples

3.2. Bearing response

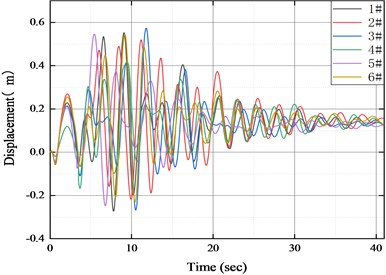
The suspension bridge pylon and the main beam are connected by double bearings. The bearing response in the finite element model is determined by the relative displacement of the main girder node connected to the bearing and the bridge node. Because the displacement response of the double bearings is the same, as a representative, the longitudinal displacement response of only one of the bearings is given here, as shown in Fig. 3. It can be seen from the figure that the response trend of the bearings under different ground shaking is relatively consistent, and the extreme values of the response are 0.55 m, 0.52 m, 0.57 m, 0.42 m, 0.55 m and 0.54 m. After the earthquake, the bearing displacement did not return to the zero line, indicating that the main beam had an irreversible overall longitudinal drift under the earthquake.

Fig. 3Displacement of suspension bridge bearing

3.3. Bridge pylon response

Fig. 4 draws the cross-section layout of the bridge pylon. Here, section 1-1 and section 2-2 are selected as representatives for response analysis. Fig. 5 show the longitudinal bending moment-curvature hysteresis curves of the 1-1 and 2-2 sections under the action of the 1# ground motion sample, from which the obvious nonlinear characteristics of the bridge pylon can be observed. The maximum curvature of section 1-1 in the longitudinal direction is 1.75×10^-4 m^-1 and the corresponding bending moment is 3.83×10⁸ N∙m, which is larger than the corresponding curvature of section 2-2 of 2.58×10^-4 m^-1 and bending moment of 3.73×10⁸ N∙m.

Fig. 6 shows the longitudinal curvature responses of the two sections of the bridge tower under the action of six representative ground motion samples. It can be seen that under the excitation of three-dimensional ground motions, the curvatures of Sec 1-1 and 2-2 in the longitudinal bridge direction have consistent fluctuation laws, and the curvature response of Sec 1-1 is slightly larger than that of Sec 2-2. The maximum curvature value of the bridge tower appears in the first 15 s of the ground motion, which is consistent with the spectral characteristics of random ground motion generated by the simulation.

Fig. 4Bridge pylon layout

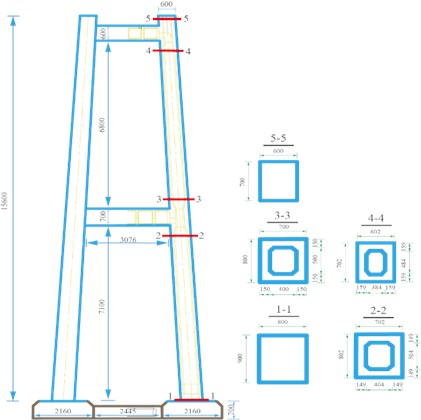
Fig. 5Longitudinal hysteresis curves of pylons Sec1-1 and Sec2-2

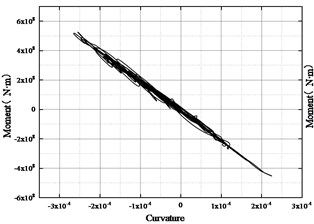
a) Sec1-1

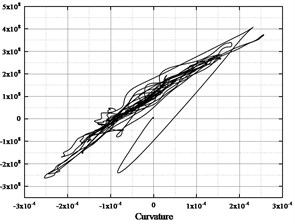
b) Sec2-2

Fig. 6Longitudinal section curvature of bridge pylon under sample ground motion

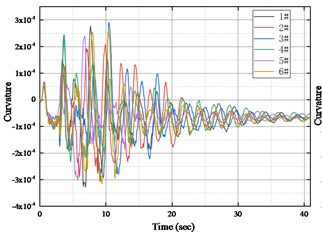
a) Sec1-1

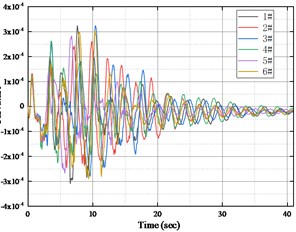
b) Sec2-2

4. Conclusions

In this paper, a finite element model is first established by taking an actual large-span single-pylon suspension bridge in Southwest China as an example. Then, the stochastic function method based on Priestley's evolution spectrum theory is used to simulate the ground motion with dimensionality reduction, and the obtained ground motion samples are input into the finite element model of the suspension bridge. Finally, the pylon bearing displacement and the pylon section curvature of the suspension bridge are analyzed. The results show that:

1) The random ground motion samples of dimension reduction simulation are efficient and accurate, and can be better suitable for the seismic response analysis of structures. Under the ground motion with PGA 0.4 g, the seismic response of the bearing and pylon showed obvious nonlinear characteristics.

2) The extreme value of the relative displacement of the pylon bearing is too large, and an irreversible drift occurs between the main girder and the pylon; the curvature of the longitudinal section of the pylon mainly shows a decreasing trend along the height, while the curvature of the transverse section shows an increasing trend.

3) The longitudinal curvature disturbance of the 1-1 and 2-2 sections of the bridge tower is relatively consistent, the maximum curvature of the 1-1 section is slightly larger than that of the 2-2 section; the transverse section 1-1 has a larger curvature in the first 5s. Disturbance, the peak value of the response under the action of vibration in various places is also significantly higher than that of section 2-2.