Prediction of structural dynamic response based on transfer function

1. Introduction

Because the dynamic response of a structure under earthquake action is an important foundation for studying and evaluating the structure's seismic performance, obtaining the dynamic response of the structure is essential. For structural seismic response, although it can also be analyzed based on finite element numerical simulation, we need to establish a complex finite element model according to the relevant design drawings of the building, and then input simulation analysis for each ground motion to get the corresponding results. In the process of analysis, not only strict theoretical support is needed, but also the selection and establishment of finite element model, processing of boundary conditions, selection of ground motion input and analysis methods need to be solved one by one. For structures with detailed design data, finite element numerical simulation can be used to obtain the structural dynamic response of the target building. However, the finite element model cannot be established for the structure without detailed design data. Therefore, this paper will calculate the transfer function [1-3] of the target building based on the strong ground motions. Then a structural response prediction model is established based on the transfer function, and the structural response is analyzed. The obtained results are accurate to the numerical simulation results, which provides a new analysis method for predicting the structural response of buildings without design data information.

2. Transfer function

Generally, the motion equation of a multi-degree-of-freedom system can be expressed as:

where, $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$ and are respectively the mass matrix, damping matrix and stiffness matrix of the structure. $\left\{f\right(t\left)\right\}$ and $\left\{y\right(t\left)\right\}$ respectively represent the excitation force vector and the displacement response vector of the structure.

According to Eq. (1), the transfer function of the structure can be obtained by the ratio of Fourier spectrum [4] amplitudes of the reaction (output) and excitation (input) of the structure, expressed as follows:

where, $F\left(\omega \right)$ and$Y\left(\omega \right)$ is the Fourier transform, $\left[F_2\right(\omega \left)\mathrm{*}H\right(\omega ){]}^{-1}$ is the inverse Fourier transform, and $y_2$ is the time series of the predicted structural reaction. For buildings with rich strong earthquake records, even though we cannot know the specific information of the actual structure, we can use the transfer function to solve the cycle iteration and establish the prediction model of the structural response to predict the structural response. This paper is based on such ideas to predict the seismic response of building structures.

Fig. 1Schematic diagram of TKD architecture

3. Structural response prediction based on transfer function

With the increasing number of strong earthquake observation stations in buildings, a sea of strong ground motions accumulated. The transfer function of the building can be calculated based on strong ground motions at two locations (one considered as input and the other as output). In this paper, a high-rise Building (TKD [5-6]) with rich strong earthquake records in Japan Building Research Institute Strong Motion Network (BRI Strong Motion Network: https://smo.kenken.go.jp/ [7]) is selected as an example to illustrate. TKD is a high-rise building located in Tokyo, Japan, with a 20-year strong ground motion (as shown in Fig. 1). Its dynamic characteristics changed significantly before and after the Great East Japan Earthquake [8], so it is very important to accurately obtain the structural response for the evaluation of its structural performance. First, we divided the strong earthquake records of TKD of the selected target building into many groups according to the earthquake onset time, and each group included a certain number of ground motions. Then we constructed a transfer function model based on the ground motions of each group. Choosing the ground for the input of strong earthquake records, the structure is at the top of strong earthquake records for the output (as shown in Fig. 2), transfer function is obtained by input-output algorithm, in order to improve the stability of the model, we set up the loop iteration solving input - output on average transfer function, construct the prediction model of transfer function is stable. After the training of the model, the new ground motion (artificial wave or natural wave) is input, and then the Fourier transform is carried out, and the corresponding structural acceleration response and structural displacement response under the ground motion can be obtained by inverse calculation of the transfer function.

Fig. 2A strong ground motion of TKD building

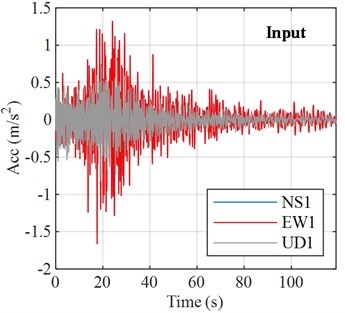
a) Input signals

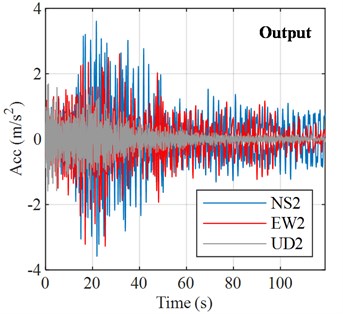
b) Output signals

Fig. 3Schematic diagram of predicting structural response based on transfer function

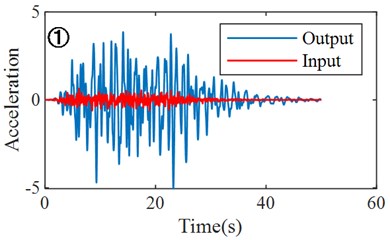
a) Input-Output acceleration

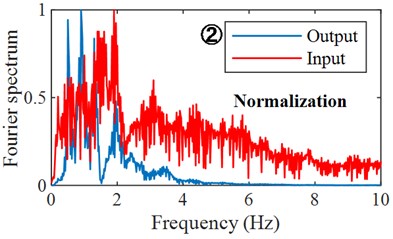
b) Input-Output Fourier spectrum ratio

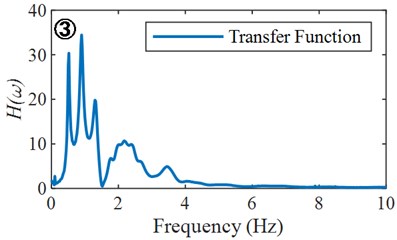
c) Transfer function

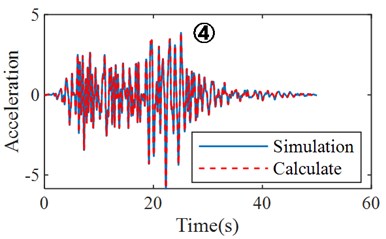
d) Results of calculation and simulation

Fig. 3 clearly shows the prediction steps and results of a structural response of ground motion. By comparing the prediction results with the actual numerical values, the PGA and frequency domain characteristics of the time-history curve are basically consistent, indicating the effectiveness and reliability of structural response prediction based on the transfer function. Fig. 4 shows the structural acceleration response and displacement response predicted based on the transfer function model with an input acceleration time-history curve. Fig. 5 shows the Fourier spectrum and response spectrum curves obtained from the predicted acceleration response. According to the predicted structural response, the performance of the structure can be analyzed, and the dynamic characteristics and reaction spectrum of the structure can be obtained, which provides a reference for the performance evaluation of the structure.

Fig. 4The acceleration and displacement responses of structures are predicted based on transfer function

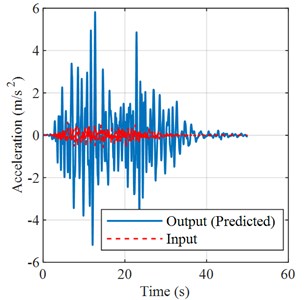
a) Acceleration response

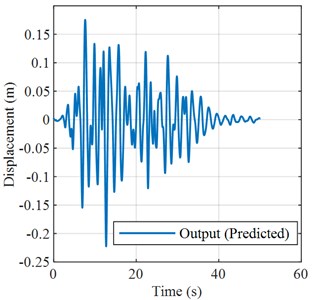
b) Displacement response

Fig. 5Fourier and response spectra of predicted structural response

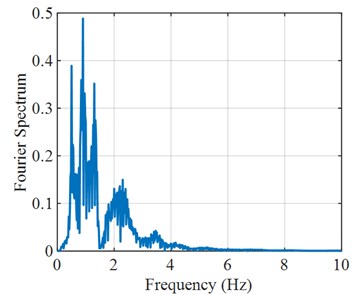
a) Fourier spectrum of prediction result

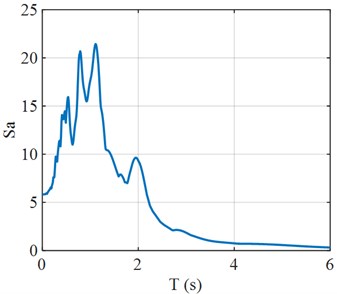
b) Response spectrum of prediction result

4. Conclusions

In this paper, based on the transfer function to establish the structural response prediction model, the dynamic response of the structure, and the prediction results are excellent. The proposed method for predicting structural response based on transfer function provides a new analytical method for predicting structural response of buildings without design information.