Abstract
Imbalanced faults are common and highly harmful faults in the rotating machinery, and the causes of imbalance are various. To better establish a unified cognitive form of imbalance fault health states, a series of experiments are designed to explore the signal changes of the rotating system under different imbalance states, and a Mahalanobis distance (MD) metric learning method based on feature extraction in the time domain and frequency domain is proposed. Finally, the mapping relations between unbalance moments and confidence values (CV) are constructed, which the proposed equivalent health assessment (EHA). The verification results prove that the proposed EHA is effective for accurately knowing the health degree of the given rotating system under imbalance states.
1. Introduction
With the rapid development of industrial technology, high-speed rotating machinery has also emerged. As the core component of rotating machinery, the rotor is one of the most prone to failure. Several factors can cause the rotor’ s central inertial major axis to deviate from its axis of rotation. Field statistics show that 95 % of the exciting force causing excessive vibration is the imbalance force of the rotor [1]. It is the main excitation source of the rotating machinery and the triggering factor of various self-excited vibrations.
In terms of the imbalance faults detection, Antonino et al. [2]. used multi-regime current to diagnose the cage pump in both steady-state and startup states. Guo et al. [3]. established a 3D finite element model for the fatigue simulation experiment of a breathing cracked rotor and obtained results of the residual life assessment. Carbajal-Hern et al. [4]. used transient current to analyze the fault characteristics of induction motor with multiple features, and obtained the diagnosis results of different faults with mechanical origin. Sarmah et al. [5]. developed a method based on complex frequency domain EOMs to estimate some fault parameters of rotors. Shrivastava et al. [6]. experimentally verified a Kalman filter-based methodology utilizing frequency domain parameter estimation. Li Zhao et al. [7]. facilitated researches on dynamic features of rotors with axial imbalance mass distribution, offering theoretical basis including the lumped mass means for fault diagnosis.
In terms of the health assessment in rotating machinery, some research has been done all over the world on the state assessment. Qiu and Lee et al. [8]. established a rolling bearings performance degradation assessment method based on optimal wavelet filter and self-organizing feature map. Ben Ali et al. [9] combined EMD with an artificial neural network to realize the classification of rolling bearing defects and the evaluation of whole life performance degradation. Soualhi et al. [10]. achieved the bearing degradation detection utilizing the combination of support vector machine and support vector regression, combined with data-driven and experience-driven methods. Tiwari et al. [11]. used a new technique of self-adaptive signal decomposition, namely concealed component decomposition, together with a proposed mode selection criterion. Kumar et al. [12]. facilitated remaining life assessment utilizing Kullback-Leibler divergence with Gaussian processes regression. Xu et al. [13]. presented ensemble empirical mode decomposition as well as affinity propagation clustering in order to assess the health status of bearings. Cui et al [14]. defined multidimensional frequency-domain health characteristics to propose a learning-based health model quantitatively evaluating bearing health. In the rotor imbalance fault, X Shen et al. [15]. studied the vibration characteristics of a friction-impact rotor-bearing system excited by mass imbalance.
Combined with previous works, in the rotating system, imbalance faults can be expressed by a variety of signals, and the health assessment of the rotating system in the imbalance state still needs further research. Especially, it is costly to diagnose specific patterns of imbalance only from vibration signals, so we should better establish a unified cognitive form of imbalance fault health states. The essence of imbalance is the imbalance of moment, which is the basis of the proposed EHA.
Therefore, we design a variety of imbalance state experiments in this paper, collect the vibration signals in two directions, extract the deviation characteristics in the signal, use the distance metric learning algorithm to obtain the deviation degree of each fault state compared to the normal state, and calibration the deviation degree under given imbalance states. The mapping relations between unbalance moments and confidence values (CV) are constructed finally, which the proposed EHA. When a certain imbalance fault occurs, we can perceive the actual health degree only by calculating the imbalance moment, and provide information support for device health management.
The organizational structure of this paper is as follows: the second chapter introduces the health assessment approach, the third chapter introduces the process of experimental design and signal processing, and in the fourth chapter, the conclusions are summarized.
Fig. 1The flow chart of health assessment approach
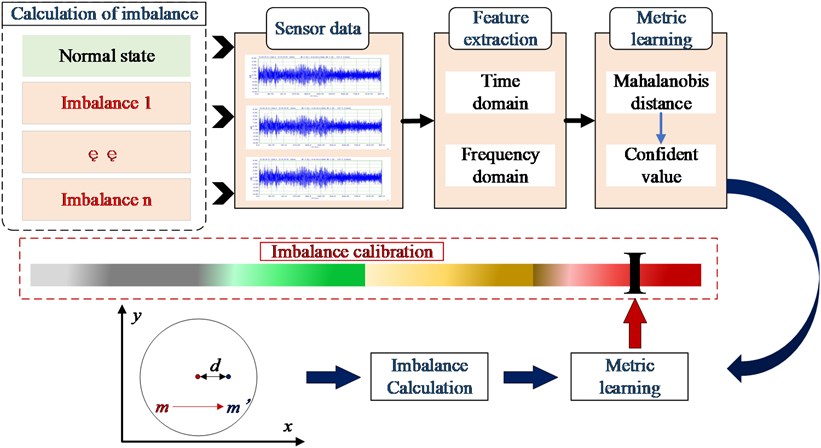
2. Health assessment approach
The flow chart of the method proposed in this paper is shown in Fig. 1, which mainly includes three parts, feature extraction, imbalance calculation, and metric learning. Feature extraction needs to filter out features that can distinguish different states. Imbalance calculation is the acquisition of an unbalanced moment. In addition, features should be considered from multiple dimensions to ensure the utilization of favorable information. Metric learning requires algorithms that can be used to characterize the degree of deviation of each fault state.
2.1. Feature extraction
Three features in time domain and frequency domain are utilized in the proposed approach.
2.1.1. Root-mean-square
Effective value is also known as vibration intensity, which used to reflect the vibration level of mechanical equipment.
2.1.2. Margin factor
The non-coaxial rotor may cause the change of signal margin factor, which is sensitive to mechanical wear failure:
2.1.3. Single-sided amplitude
In this paper, the vibration signal is processed by Fast Fourier Transform Algorithm, and the single-sided amplitude of working frequency is taken as the measurement feature.
2.2. Metric learning
According to the characteristics of vibration signal and the extracted features, we choose Mahalanobis distance as the main algorithm of metric learning.
Then calculate the Mahalanobis distance as follows:
– Calculate the average of each characteristic vector:
– Calculate the standard deviation of each feature vector:
The feature vector is orthogonal to get, then transpose 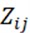 :
:
– Calculate the correlation matrix :
The Mahalanobis distance is:
After the sensor vibration signal is obtained and the features are extracted, we took the feature points of the bearing under normal conditions.
Calculate the distance between each state point and the normal state in turn.
The larger the MD distance, the farther the current characteristic point is from the normal space, demonstrating the worse degradation of performance. The smaller the MD, the closer the current characteristic point is to the normal space, indicating a healthier bearing. In order to more intuitively represent the current health status of the bearing, the MD is normalized to the Confidence Value (CV), i.e. the bearing health assessment results are represented by CV. The higher the CV value, the better the bearing performance. When the CV value is close to 1, it is generally considered that the bearing operates in a completely normal state. The smaller the CV value is, the worse the bearing performance is degraded. If the CV value is close to 0, the bearing failure is generally considered to have a relatively high degree and cannot continue to work.
The normalized algorithm in this paper is as follows:
where is the normalized parameter, and is set to a different parameter value, then the sensitivity of the corresponding CV value to the fault trend of different failure stages will change, so the evaluation model can be adjusted according to the actual situation and needs.
2.3. Imbalance calculation
In this paper, we use a classical formula for the calculation of imbalance moment, as shown in Eq. (11). In Eq. (11), stands for imbalance moment, stands for the original rotor mass, stands for the mass of the imbalanced rotor, and stands for the offset distance of the mass center:
3. Experimental design
The experiment is carried out on the Machinery Fault Simulator (MFS) test-bed in the PHM lab, Beihang University. In the experiment, 8 kinds of non-coaxial faults are injected respectively, and a normal state is a regarded as the reference, and the fault injection position and the reception position of the bearing vibration signal are indicated in Fig. 2.
18 threaded holes distributed on the rotor uniformly, with the rotor centroid as the origin point, so the angles between every two threaded holes is 20°. Different non-coaxial rotor faults can be injected by installing screws.
The working frequency is set as 30 Hz, and the sampling frequency is 40 kHz, and 4 s vibration signal is acquired in each state.
3.1. Fault injection
All injected faults in this experiment are shown in Table 1. The red dots represent the screw locations of fault injection, and their imbalance moment values can be seen in Table 1.
Table 1Fault injection and imbalance moment
Fault injection | 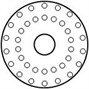 | 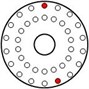 | 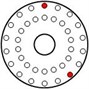 |
Imbalance moment (g·mm) | 0 | 94.7 | 183.6 |
Fault injection | 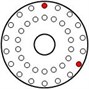 | 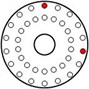 | 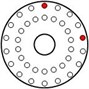 |
Imbalance moment (g·mm) | 268.5 | 345.1 | 411.3 |
Fault injection |  |  |  |
Imbalance moment (g·mm) | 465.0 | 504.5 | 528.7 |
Fig. 2Schematic diagram of experimental design

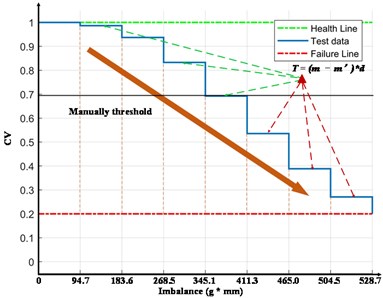
Fig. 3CV vs. different imbalance states
3.2. Signal processing and results
In signal processing, we consider the vibration signals in two dimensions (-axis and -axis) at the same time. We can achieve the Mahalanobis distances in two dimensions under different states after constructing the feature vectors. The distribution of MD in two directions is similar, which proves that the influence and change of different imbalance state on two directions are similar. Significantly, as the Angle between the two screws decreases, the MD increases in both directions. In order to exhibit the changes in the health state better, we calculate the distance from the origin of each point in Fig. 3 and normalized it to the health degree, namely CV.
In Fig. 3, in order to intuitively present the decline of health, we set the health line and the failure line, both of which are relative values and can be changed according to the actual situation.
The relationship between the given unbalanced moment and CV can be obtained by metric learning. When a certain imbalance fault occurs, we can perceive the actual health degree only by calculating the imbalance moment, and that is how EHA works.
Similar with Fig. 3, the health degree presents a decline like a linear state, and its trend is consistent with the actual fault situation, which indicates that the method proposed in this paper is effective for the identification and evaluation of rotor imbalance faults.
4. Conclusions
Imbalance faults are one of the most common faults in a rotating system and can trigger multiple coupling faults. In order to better establish a unified cognitive form of imbalance fault health states, we propose EHA based on metric learning to construct the mapping relations between imbalance moment and CV. Through the mechanical fault simulation test bench design of 9 different states of the comparative experiment, the vibration signals are obtained respectively by different degrees of rotor centroid migration fault injection. Then, the method proposed in this paper is used to analyze the collected vibration signals in the time domain and frequency domain. Then, the deviation degree of each state from the normal state is measured by using the MD algorithm, that is, the confidence value. After imbalance calculation, imbalance calibration, and metric learning, we can get the EHA results. The results show that the deviation degree of the rotor’s centroid will reduce the health of the rotating system. At the same time, the method proposed in this paper is effective for the identification and evaluation of rotor imbalance faults.
References
-
Wen Xudong et al., Nonlinear Dynamics Theory and Experiment of Fault Rotating Machinery. (in Chinese), Beijing: Science Press.
-
J. Antonino-Daviu, V. Climente-Alarcon, A. Quijano-Lopez, and V. Fuster-Roig, “Multi-regime current analysis for the rotor health assessment in cage pump motors: case stories,” in 2016 XXII International Conference on Electrical Machines (ICEM), pp. 2924–2930, Sep. 2016, https://doi.org/10.1109/icelmach.2016.7732939
-
Guo C. et al., “A combined mode-based fatigue life assessment method for a breathing cracked rotor,” in Prognostics and System Health Management Conference, 2017.
-
J. Juan Carbajal-Hernández, L. P. Sánchez-Fernández, I. Hernández-Bautista, J. J. Medel-Juárez, and L. A. Sánchez-Pérez, “Classification of unbalance and misalignment in induction motors using orbital analysis and associative memories,” Neurocomputing, Vol. 175, pp. 838–850, Jan. 2016, https://doi.org/10.1016/j.neucom.2015.06.094
-
N. Sarmah and R. Tiwari, “Analysis and identification of the additive and multiplicative fault parameters in a cracked-bowed-unbalanced rotor system integrated with an auxiliary active magnetic bearing,” Mechanism and Machine Theory, Vol. 146, p. 103744, Apr. 2020, https://doi.org/10.1016/j.mechmachtheory.2019.103744
-
A. Shrivastava and A. Mohanty, “Identification of unbalance in a rotor-bearing system using Kalman filter-based input estimation technique,” Journal of Vibration and Control, pp. 1081–1091, 2019.
-
L. Zhao, H. Zhang, Y. Liu, and C. Zhou, “Nonlinear dynamic characteristics of multidisk rod fastening rotor with axial unbalance mass distribution,” Shock and Vibration, Vol. 2022, pp. 1–14, Mar. 2022, https://doi.org/10.1155/2022/8094476
-
H. Qiu, J. Lee, J. Lin, and G. Yu, “Robust performance degradation assessment methods for enhanced rolling element bearing prognostics,” Advanced Engineering Informatics, Vol. 17, No. 3-4, pp. 127–140, Jul. 2003, https://doi.org/10.1016/j.aei.2004.08.001
-
J. Ben Ali, N. Fnaiech, L. Saidi, B. Chebel-Morello, and F. Fnaiech, “Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals,” Applied Acoustics, Vol. 89, pp. 16–27, Mar. 2015, https://doi.org/10.1016/j.apacoust.2014.08.016
-
A. Soualhi, K. Medjaher, and N. Zerhouni, “Bearing health monitoring based on Hilbert-Huang transform, support vector machine, and regression,” IEEE Transactions on Instrumentation and Measurement, Vol. 64, No. 1, pp. 52–62, Jan. 2015, https://doi.org/10.1109/tim.2014.2330494
-
P. Tiwari and S. H. Upadhyay, “Novel self-adaptive vibration signal analysis: concealed component decomposition and its application in bearing fault diagnosis,” Journal of Sound and Vibration, Vol. 502, p. 116079, Jun. 2021, https://doi.org/10.1016/j.jsv.2021.116079
-
P. Shankar Kumar, L. A. Kumaraswamidhas, and S. K. Laha, “Bearing Degradation Assessment and Remaining Useful Life Estimation Based on Kullback-Leibler Divergence and Gaussian Processes Regression,” Measurement, Vol. 174, p. 108948, Apr. 2021, https://doi.org/10.1016/j.measurement.2020.108948
-
F. Xu, X. Song, K.-L. Tsui, F. Yang, and Z. Huang, “Bearing performance degradation assessment based on ensemble empirical mode decomposition and affinity propagation clustering,” IEEE Access, Vol. 7, No. 99, pp. 54623–54637, 2019, https://doi.org/10.1109/access.2019.2913186
-
J. Cui, L. Ren, X. Wang, and L. Zhang, “Pairwise comparison learning based bearing health quantitative modeling and its application in service life prediction,” Future Generation Computer Systems, Vol. 97, pp. 578–586, Aug. 2019, https://doi.org/10.1016/j.future.2019.03.026
-
Xiaoyao Shen, Jiuhong Jia, and Mein Zhao, “Numerical analysis of a rub-impact rotor-bearing system with mass unbalance,” Journal of Vibration and Control, Vol. 13, No. 12, pp. 1819–1834, Dec. 2007, https://doi.org/10.1177/1077546307080029
