Rolling bearing health status assessment based on ITD-GMM method

1. Introduction

In the field of mechanical transmission, rolling bearing is one of the most widely used parts, and its operating condition can directly affect the reliability and service life of the system [1]. Rolling often has the characteristics of easy failure, and the bearing degradation is one of the main reasons for its failure. Therefore, quantitative analysis of the bearing's health status plays an important role in monitoring bearing performance, providing repair and maintenance strategies. At present, the vibration signal becomes mostly used for the performance monitoring of rolling bearings, because it implies useful information reflecting the location and extent of the fault [2-4]. Analyzing and mining the vibration signal can help to understand the bearing status and predict the effective residual life so as to lay a foundation for health management.

The assessment of performance degradation of rolling bearing by using the bearing current and prior information to quantify the severity of its performance degradation has aroused widespread concern in scholars. Different scholars have made some corresponding researches according to the feature extraction, pattern recognition, distance metric learning of the vibration signals of the bearing. Based on the non-stationary characteristics of the vibration signal, Chen Lu et al. [5] used EMD (Empirical Mode Decomposition) to decompose a set of intrinsic mode function and used SOM (Self-organizing Maps) to evaluate and forecast the performance degradation of the bearing. Chao Lu et al. [6] used LSSVM (Least squares support vector machine) and other methods to predict the trend of performance degradation for small sample data of slewing bearing. He Yu et al. [7] adopted the method of LCD (Local feature scale decomposition) instead of EMD to make feature extraction more efficient and restrain the end effect.

Although the researches mentioned above have laid a certain foundation for the assessment and prediction of performance degradation of rolling bearing, there are still some problems, such as the large amount of calculation of LS-SVM and the low convergence speed of SOM network and so on. In recent years, with the further development of machine learning algorithm, many new algorithms provided a new way about the performance degradation assessment of rolling bearings.

In order to solve the above problems and enhance the accuracy of the performance degradation assessment, in this paper, a new method is proposed as follows. Combined with the intrinsic time-scale decomposition and Gaussian mixture model, the bearing characteristics were extracted. Based on the statistical theory, the quantitative analysis of the bearing degeneration state was further carried out. ITD has the advantage of fewer iterations and less edge effects, which makes it can accurately extract the dynamic characteristics of non-stationary signals [8]. As a result, it is suitable for real-time on-line processing of data. The GMM model is used to fit the probability distribution of the characteristic signal of the vibration signal in the early stage of fault-free phase [9]. Based on this, the probability of the following vibration signal eigenvector belong to the model is obtained, and the coincidence degree is used as a quantitative evaluation indicator of the bearing performance degradation.

2. Methodology

2.2. Gaussian mixture model

For a random variable $Y={[Y_1,\dots ,Y_d]}^T$, $y={[y_1,\dots ,y_d]}^T$ is a case of it. If the probability density function of $Y$ can be written as follows:

5

$p\left(y|\mathrm{\Theta }\right)=\sum _{m=1}^k{a}_{m}p\left(y|{\theta }_m\right).$

Then $Y$ is object to finite mixture distribution and the model of $Y$ is the finite mixture model. For ($a_1$, …, $a_m$) is the probability of every component distribution. ${\theta }_m$ is the parameter of the m component distribution. At the same time, $a_m$ must fit the demand:

6

$a_m\ge 0,m=1,\dots ,k,\sum _{m=1}^k{a}_m=1.$

If all the components are Gaussian distributions, then the corresponding model is the Gaussian Mixture Model (GMM).

Fig. 1The procedure of the proposed methodology

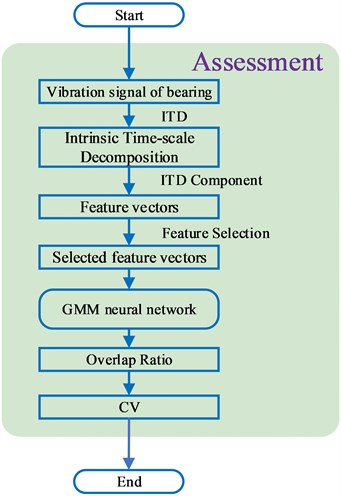
3. Case study

In this paper, the Bearing Prognostics Simulator produced by Spectra Quest was used to verify the effectiveness of the algorithm, and the data experiment table was shown in Fig. 2. The working condition of bearing was set at constant speed of 2000 rpm. The vibration sensor was set in both the horizontal and vertical direction of the bearing to collect its vibration signal, and the sampling frequency was set to 10 kHz. After data preprocessing, the data of normal non-degradation trend and the data of degradation trend of 200,000 points were obtained.

Fig. 2Bearing prognostics simulator

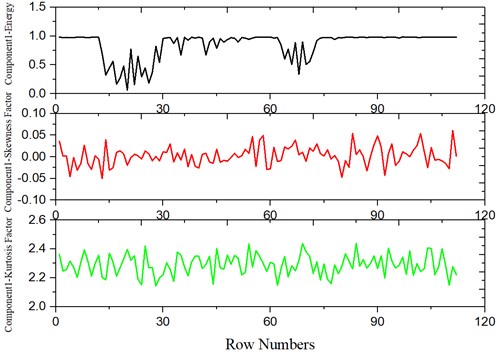
For bearing health assessment, every 200000 points was taken as a group. The original vibration signal was decomposed by the ITD method. The time domain features were extracted from every 2000 points for the obtained decomposition amount, and the characteristic vector was obtained. The features extracted included energy, kurtosis, and skewness. The time domain characteristics of Component1 without degradation trend obtained by ITD decomposition were shown in Fig. 3.

Fig. 3The features of Component1

The GMM model was trained by using normal non-degenerate data, and then the data of degenerative trend was fed into the data model to compute the matching degree between the data and the model through the method of mathematical statistics. Finally, the results obtained were normalized to a CV value of 0-1 to express the bearing health status intuitively. The normalized health curve was shown in Fig. 4.

Fig. 4The normalized health curve of bearing

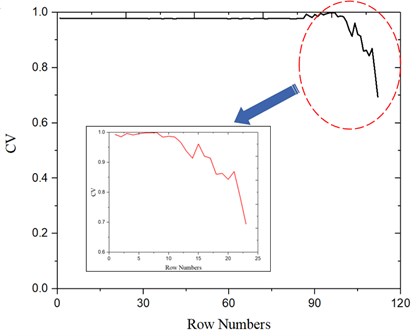
As can be seen from Fig. 4, the closer the CV value is to 1, the better the health of the bearing. In the early stage, the CV value of the bearing stabilized at a state of about 0.98. With the passage of time, the CV value of the bearing showed a downward trend. Moreover, the CV value decreased from 0.98 to 0.7 in the interval of only 10 points, indicating that the performance of the bearing experienced a sharp decline in a short period of time, which may be related to the accumulation of internal damage in the bearing. The experimental results showed that using ITD-GMM can be a good assessment of the health status.

4. Conclusions

This work presented a method for performance degradation assessment and fault diagnosis of bearing by using ITD and GMM. The advantage of the proposed method lies in the feature extraction which enables fully exploit the information in the signal. Moreover, GMM was introduced to assess the health state of bearing, and the mass data was evaluated by means of statistical method. The feasibility and effectiveness of the proposed method were verified by an experiment.