Vehicle-bridge coupling dynamic response of a box bridge after reinforcement with prestressed CFRP

1. Introduction

Because of the complex environment of the current transportation industry, the overloading of large trucks has become a common phenomenon. The movements of these large vehicles cause large vibrations and shocks on bridges, leading to large deflection and stress that seriously impact the safety of the bridge. Therefore, it is necessary to analyze the vehicle-bridge coupled dynamic response before and after reinforcement with prestressed CFRP, and much progress has been achieved in the study of bridge reinforcement.

Scholars, such as Ai et al. [1], have derived the quantitative relationship between the natural frequencies of pretension and the damage of RC beams theoretically. Omar [2] studied the shear fatigue behavior of reinforced concrete (RC) T-beams strengthened with carbon fiber reinforced polymer (CFRP) composite materials and obtained the effectiveness of a CFRP strengthening system for prolonging the fatigue life of structures via experiments. Yang et al.[3] used the Hertz elastic contact model to calculate the dynamic equation of the moving wheel-track-bridge coupling element that considers track irregularity. Lu et al. [4] tested the dynamic characteristics of intact RC beams strengthened with prestressed CFRP. Zhao and Chen [5] conducted a reliability performance test along with theoretical and finite element analysis of the anchorage system to study the reliability and effectiveness of a prestressed CFRP plate anchoring system. Guo and Wang [6] conducted precision analysis regarding the technical difficulties of CFRP carbon fiber plate tension and prestressed damage based on long-term monitoring. Zhang et al. [7] analyzed the beam deflection and stress in fibers to determine the working condition of a prestressed CFRP/GFRP fiber reinforced structure. Khelifa et al. [8] tested and analyzed the bending behavior of finger-jointed timber (spruce) beams reinforced with CFRP material. Baikaiyi[9] participated in analyzing CFRP alms plus special prestressed tensioning equipment research and development with prestressed CFRP cloth in concrete bridge reinforcement technology as the main research object and proposed the construction technology, construction procedure and key construction technology of a prestressed CFRP reinforced concrete bridge. Li [10] studied the properties of FRP materials and prestress application methods and conducted a prestressed CFRP reinforced concrete beam bending test; based on the results, the mechanical characteristics of beam reinforcement were discussed. Davood et al. [11] studied the influence of the EBRIG method and EBR method on the shear strengthening of structural members under different installation techniques of CFRP plates via experiments. Wang and Zhao [12] used train-bridge coupling vibration relationships to establish a single-beam vehicle differential equation of bridge motion, through the deformation coordination and interaction force coordination, realized the coupling relation between vehicles and bridges.

In the research of vehicle-bridge coupling model, Nguyen et al. [13] proposed the wind-vehicle-bridge interaction model, the vehicle is modeled as a multi-body system. Through the interaction between the moving contact and the bridge, the road irregularity is also simulated. A general user element is proposed and implemented by a general finite element software. Li et al. [14] thought that a single software is not enough for vehicle bridge coupling analysis, so they proposed an interactive analysis method combining commercial finite element software ANSYS and multi-body system software SIMPACK. Yao et al. [15] gave an idea of building road roughness model in vehicle bridge interaction (VBI) system, which is equivalent to two external forces acting on vehicle bridge subsystem. Miguel et al. [16] gave a new method to apply TMD and MTMD robust design optimization method to vehicle-bridge coupled vibration problem.

In summary, the existing literature has provided a considerable amount of theoretical analysis and experimental data regarding the dynamic response of vehicle-bridge coupling and prestressed CFRP reinforced beams and bridge piers. Nevertheless, at present, the prestressed CFRP reinforcement test is mainly applied using small-size beams and columns, especially for prestressed reinforcement technology; regarding the pre-tensioning method or post-tensioning method, research on long-span bridges and large-size piers is lacking. The study of the dynamic response under a vehicle moving load after bridge reinforcement of vehicle-bridge coupling is also very rare. Therefore, in this paper, the dynamic response of vehicle-bridge coupling of a prestressed concrete box bridge before and after reinforcement is analyzed. By using finite element software in combination with the data of an actual bridge, a numerical vehicle-bridge coupled model before and after reinforcement with CFRP is established, and the influence of different speeds of heavy vehicles on the dynamic response of vehicle-bridge vibration coupling before and after reinforcement with post-tensioned prestressed CFRP is studied.

2. Vehicle moving loads

2.1. Theory of moving constant force

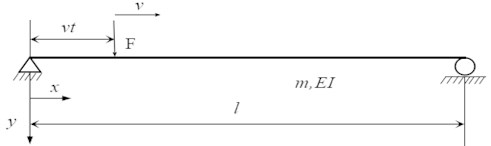
Under the action of a moving load, the stress and strain of the bridge structure produces a corresponding dynamic response; thus, in the process of bridge reinforcement, the moving load of the vehicle should also be considered. Bridge dynamic load action includes the function of moving at a constant speed constant force [17], moving at a constant speed harmonic force, the action of uniform quality of rolling, etc., according to the actual situation of the box bridge; the method of moving constant force is used to apply the dynamic load because this method is relatively simple and is easier to achieve in the FEM. Taking a simply supported beam as an example, the function of moving constant force is shown in Fig. 1, where $F$ is the constant force that moves at a constant velocity v to the right, ignoring the mass of moving load in the process of analysis. The vibration equation is given as follows:

1

$EI\frac{{\partial }^{4}y(x,t)}{\partial x^4}+m\frac{{\partial }^{2}y(x,t)}{\partial x^2}=F\left(x,t\right),$

2

$y\left(x,t\right)=\sum _{n=1}^N{A}_n\left(t\right){\mathrm{\Phi }}_n\left(x\right),$

where $F\left(x,t\right)$ is the moving load, y is the series of the vibration mode, $EI$ is the flexural rigidity, $m$ is the mass, and $y\left(x,t\right)$ is the displacement of the forced vibration.

Fig. 1Constant force through a simple beam

The forced vibration equation is obtained by substituting Eq. (2) into Eq. (1). After using the orthogonality of vibration mode, the decoupled forced vibration Eq. (3) is obtained:

3

${\ddot{A}}_n\left(t\right)+{{\omega }_n}^2{A}_n\left(t\right)=\sum _{n=1}^N{B}_n\left(t\right),$

where:

${{\omega }_n}^2=\frac{EI{\int }_0^l{\left[\frac{d^2{\mathrm{\Phi }}_n\left(x\right)}{d{x}^2}\right]}^{2}dx}{m{\int }_0^l{\mathrm{\Phi }}_n^2\left(x\right)dx},B_n\left(t\right)=\frac{{\int }_0^{l}F\left(x,t\right){\mathrm{\Phi }}_n\left(x\right)dx}{m{\int }_0^l{\mathrm{\Phi }}_n^2\left(x\right)dx}.$

In a simply supported beam, ${\varphi }_n=\mathrm{s}\mathrm{i}\mathrm{n}\frac{n\pi x}{l}$, for a constant force $F$ moving at a constant speed, and the generalized excitation force is given in Eq. (4):

4

$B_n（t）=\frac{{\int }_0^{l}F\delta \left(x-vt\right){\mathrm{\Phi }}_n\left(x\right)dx}{m{\int }_0^l{\mathrm{\Phi }}_n^2\left(x\right)dx}=\frac{2F}{ml}\mathrm{s}\mathrm{i}\mathrm{n}\frac{n\pi vt}{l},\left(n=\mathrm{1,2},\cdots ,N\right),$

where $\delta \left(\eta \right)$ is the Dirac function, which is defined as: $\delta \left(\eta \right)=\left\{\begin{array}{ll}1,& \eta =0,\\ 0,& \eta \ne 0,\end{array}\right.$ so Eq. (4) can be written as Eq. (5):

5

${\ddot{A}}_n+{\omega }_n^2{A}_n=\frac{2F}{ml}\mathrm{s}\mathrm{i}\mathrm{n}\frac{n\pi vt}{l},\left(n=\mathrm{1,2},\cdots ,N\right).$

When the initial condition is static, solve Eq. (5) and input the result into Eq. (5); the dynamic response expressions are given in Eq. (6):

6

$y\left(x,t\right)=\frac{2F}{ml}\sum _{N=1}^N\frac{1}{{\omega }_n^2-{\mathrm{\Omega }}_n^2}\left(\mathrm{s}\mathrm{i}\mathrm{n}{\mathrm{\Omega }}_{n}t-\frac{{\mathrm{\Omega }}_n}{{\omega }_n}\mathrm{s}\mathrm{i}\mathrm{n}{\omega }_{n}t\right)\mathrm{s}\mathrm{i}\mathrm{n}\frac{n\pi x}{l},$

where ${\mathrm{\Omega }}_n=\frac{n\pi v}{l}$ is the generalized perturbation frequency of a moving constant force, ${\omega }_n=(\frac{n\pi }{l}{)}^2\sqrt{\frac{EI}{m}}$ is the natural frequency of the prestressed box bridge, $\mathrm{s}\mathrm{i}\mathrm{n}{\mathrm{\Omega }}_{n}t$ in the brackets represents the forced vibration, and $\frac{{\mathrm{\Omega }}_n}{{\omega }_n}\mathrm{s}\mathrm{i}\mathrm{n}{\omega }_{n}t$ represents the free vibration [18].

2.2. Transformation of vehicle moving load

The load in FEM is divided into boundary excitation and external forces, which include the structure self-gravity, the two-period constant load, the prestressing stress and the vehicle live load. For the lateral arrangement of the vehicle's live load, considering the contact area of the wheel and the bridge surface, the load of the wheel is applied to the unit of the living load position [19]. The bridge is designed as a dual-lane bridge. The specific parameters of the overloaded vehicle load are given in Table 1.

Table 1Specific parameters of the vehicle load

Project	Unit	Numerical value	Project	Unit	Numerical value
Vehicle gravity	kN	600	Distance between the wheels	m	1.8
Front axle gravity	kN	40	Width and length of the front wheel landing	m	0.3×0.2
Axial gravity	kN	2×120	Middle, rear wheel landing width and length	m	0.6×0.2
Rear axle Gravity	kN	2×160	Vehicle dimensions (length and width)	m	15×2.5
Wheel base	m	3+1.4+7+1.4

For this bridge, to better simulate the process of a vehicle entering the beam to the tail leaving the bridge (Fig. 2), the vehicle can be simulated as a dynamic load. Dynamic loads can be divided into 65 load steps because the bridge has two-way lanes. Assuming two cars move at a certain speed relative to one another at the same time through the bridge, in the process of choosing which side of the lane uses FEM to analyze the dynamic response of the bridge, the mobile vehicle is simplified by a constant force moving at a constant speed. Thus, with the more accurate simulation of the vehicle driving conditions, according to an analysis of the good properties of the bridge, it is concluded that the structure is in line with the actual situation [20].

The vehicle load is distributed on the entire bridge structure according to the principle of equivalent uniform distribution. Each time forward can be regarded as the overall advance from the last unit to the next unit and is simplified according to the principle of constant moving constant force. The whole process of the operation is shown in Fig. 2 as the vehicle moves from the beginning of the bridge to the end.

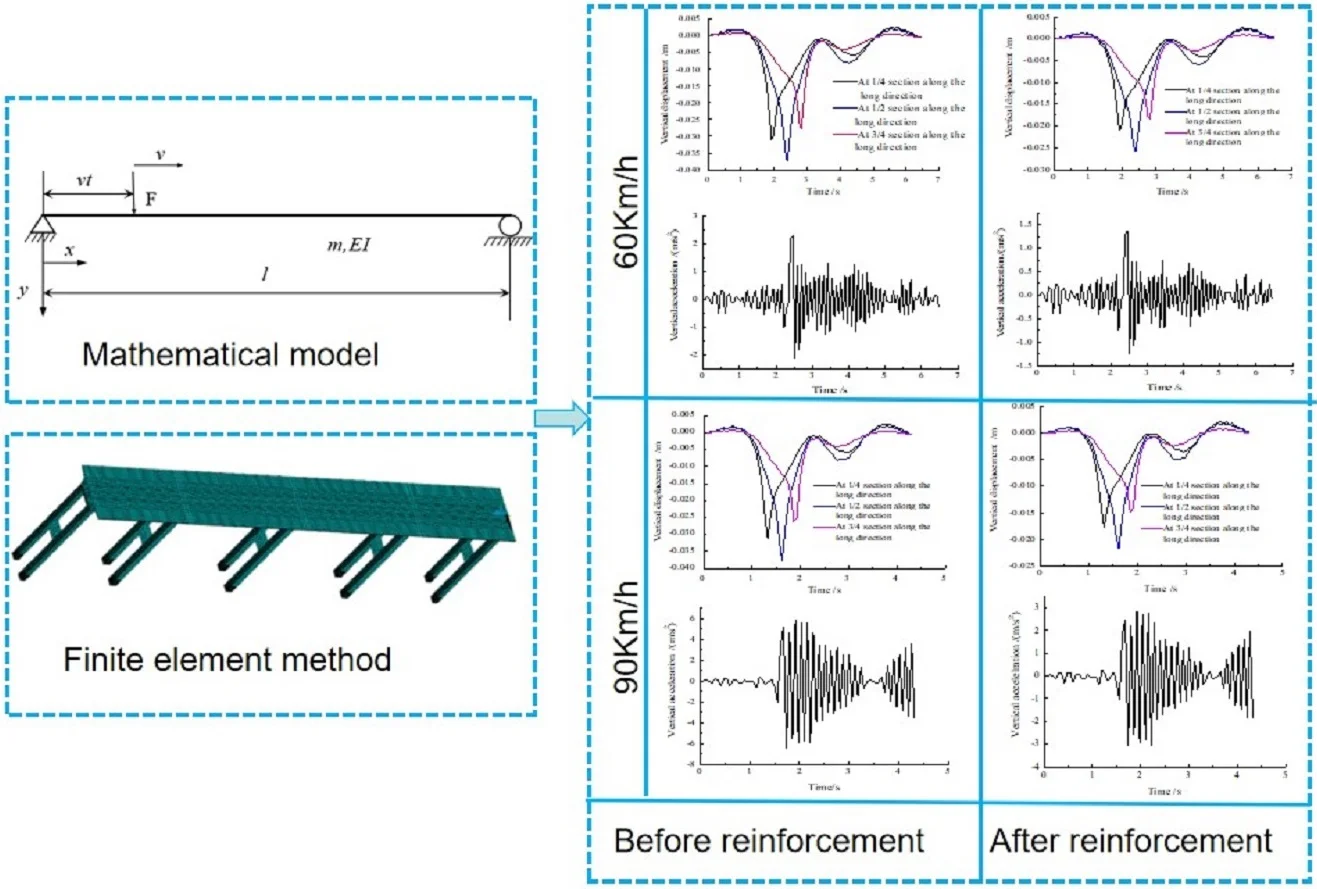
The dynamic coupling of the bridge over the overloaded vehicle is influenced by various factors, and the analysis is quite complicated. This paper only considers the influence of speed on the dynamic response of the bridge and selects a speed of 60 km/h and a speed limit of 90 km/h. In this section, with an overloaded vehicle moving at a speed of 60 km/h, the dynamic performance of the bridge is studied, and the dynamic response of the bridge before and after the reinforcement is determined.

Fig. 2Constant force through the side lane of a simple beam

3. Finite element analysis model

3.1. Pre-reinforcement model

According to the existing data, the superstructure of the main bridge has a single box with two sections, where the span arrangement is 25 m + 30 m + 30 m + 25 m and the lower structure consists of five 15-m-tall rectangular bridge piers. The box bridge is cast with 40-MPa concrete, and the pier adopts 30-MPa concrete pouring with a prestressed reinforcement strength value of $f_{pk}=$ 1860 MPa. Through observation of the bridge, it is found that some of the concrete cracked because of the long period of service and traffic due to an overload of vehicles; this cracking affects the continuous use of the bridge, with the bridge being in urgent need of reinforcement repair.

To ensure the accuracy of the numerical calculation of the whole bridge reinforced by CFRP, in this paper, FEM is used to establish the reinforced bridge model and the normal reinforcement in the box bridge; moreover, the overall layout simulation is applied uniformly in the unit, and the pier can reflect the actual reinforcement situation. The concrete unit uses the Solid65 unit, the prestressed reinforcement uses the Link8 space unit, and the carbon fiber cloth thickness is very small. Therefore, the model must use the anti-curved ability unit, and the carbon fiber cloth is simulated by shell unit Shell41. In this paper, the solid model element uses the regular hexahedral form. The box bridges are simplified as a whole; the former box bridge after meshing is shown in Fig. 3. Using the link unit to simulate prestressed reinforcement, the cooling method is used in this paper to apply the prestressed reinforcement; the prestressed reinforcement arrangement is shown in Fig. 4.

Fig. 3Box bridge model before reinforcement

Fig. 4Prestressed reinforcement arrangement

3.2. Post-tensioned reinforcement model

The carbon fiber was prestressed by post-tensioning and then anchored to the bottom of the box bridge. The prestressed carbon fiber cloth was anchored with a height of 2.5 m from the bottom of the pier. The carbon fiber cloth parameters are shown in Table 2.

Table 2Parameters of the carbon fiber cloth

Carbon fiber cloth per unit weight /(g/m2)	Design thickness /mm	Tensile strength /MPa	Modulus of elasticity /MPa	Width /mm	Spacing /mm
300	0.167	3400	2.45	150	200

Carbon fiber cloth uses the post-tensioned prestressing method because the cooling simulation in the process of tensioning structure will have a corresponding change; thus, a cooling simulation process does not well simulate the actual effect of the post-tensioning method, and the cooling iteration method must be used. In the post-tensioning process, the slip and anchor deformation between the CFRP and the anchor causes the prestress loss. According to the existing test and theoretical calculation results, the prestress loss takes up 15 % of the initial prestress; the arrangement of the CFRP is shown in Fig. 5.

Fig. 5Arrangement of the prestressed CFRP

4. Dynamic response of the vehicle-bridge coupling system

4.1. Dynamic response of the overloaded 60-km/h vehicle-bridge coupling system

4.1.1. Coupling dynamic response of the box bridge before reinforcement

(1) The side span.

Considering one overload vehicle speed of 60 km/h, based on the FEM calculation, the displacement time-history curves of the wing plate on the top section across the 1/4, 1/2, and 3/4 sections of the bridge are obtained. The curve of vertical displacement change for each section over time is shown in Fig. 6.

Fig. 6Vertical displacement time-history curves at the side spans

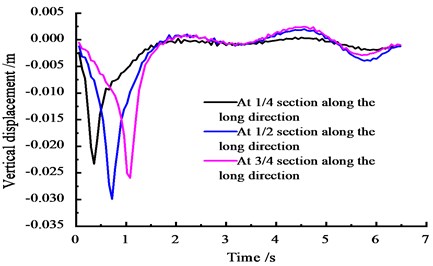
According to Fig. 6, under moving load, the vertical displacement at the 1/4 section on the side span first comes to a peak, with subsequent peaks occurring in a sequence. The vertical displacement peak of the cross section reaches a maximum peak of 0.030 m and then gradually decreases before finally ending near 7 s, which indicates that the vehicle leaves the bridge at approximately 7 s. The peak of the vertical displacement in the 1/4 section is 0.023 m, and the vertical displacement peak of the 3/4 section is 0.026 m; thus, the vertical displacement of each section is stable at 0-0.003 m and finally ends.

The acceleration time-history curves for the 1/4, 1/2, and 3/4 sections are shown in Fig. 7.

Fig. 7Vertical acceleration time-history curves at the side span

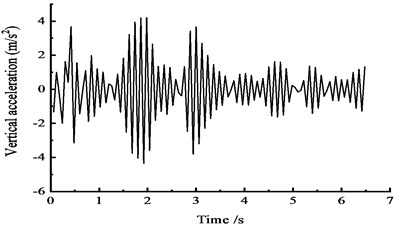
a) At the 1/4 section along the long direction

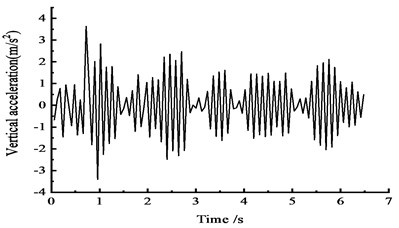
b) At the 1/2 section along the long direction

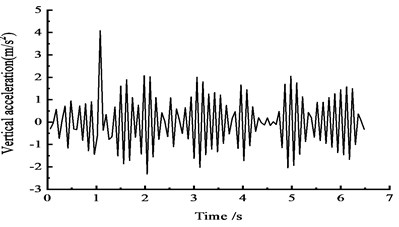
c) At the 3/4 section along the long direction

Fig. 7 shows that under the effect of vehicle moving load, the peak vertical acceleration at the 1/4 side span section reaches 4.3 m/s² at approximately 2 s, the peak vertical acceleration at the 1/2 section reaches 3.5 m/s² at approximately 1 s, and the peak vertical acceleration of 4 m/s² at the 3/4 section appears at approximately 1 s. The results show that, under moving load, the peak acceleration is smaller and closer to the cross section.

(2) The middle span.

Considering that the overload vehicle is moving at a speed of 60 km/h, based on the FEM calculation, the displacement time-history curves of the wing plate on the top section across the bridge at the 1/4, 1/2 and 3/4 sections are determined. The vertical displacement curve of each section across the bridge as the vehicle moves across with the change in time is shown in Fig. 8.

Fig. 8Vertical displacement time-history curves at the middle span

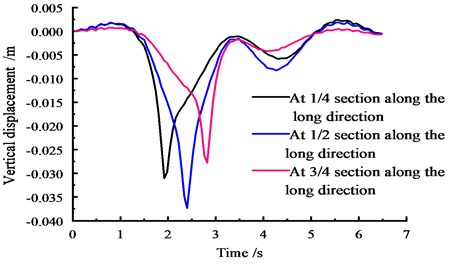
According to Fig. 8, under the moving load, the vertical displacement of the 1/4 section on the middle span first reaches a peak, and then subsequent peaks occur in sequence. The vertical displacement peak of the cross section reaches a maximum peak of 0.037 m and then gradually decreases towards both ends. The peak of the vertical displacement in the 1/4 section is 0.031 m, and the vertical displacement peak of the 3/4 section is 0.028 m. After the vertical displacement of each section reaches a peak, the trend shows large fluctuation, and the maximum vertical displacement reaches 0.010 m.

The acceleration time-history curves at the 1/4, 1/2, and 3/4 cross sections of the middle span are shown in Fig. 9.

Fig. 9Vertical acceleration time-history curves at the middle span

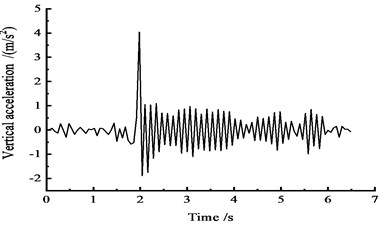
a) At the 1/4 section along the long direction

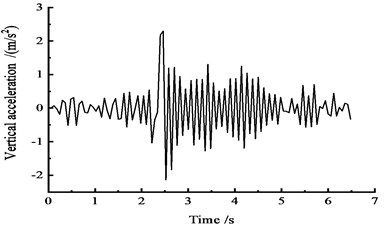
b) At the 1/2 section along the long direction

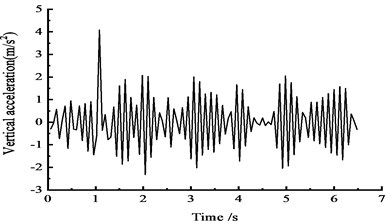
c) At the 3/4 section along the long direction

Fig. 9 shows that under the effect of vehicle moving load, the vertical acceleration of the cross section reaches a peak: the peak vertical acceleration at the 1/4 section reaches 4.0 m/s² at approximately 2 s, the peak vertical acceleration at the 1/2 section reaches 2.3 m/s² at approximately 2.5 s, and the peak vertical acceleration at the 3/4 section reaches 2.6 m/s² at approximately 3 s. In addition, the trends of the vertical acceleration time-history curves at the 1/4, 1/2 and 3/4 sections are approximately the same.

4.1.2. Coupling dynamic response of the post-tensioning box bridge after reinforcement

(1) The side span.

After reinforcement using the post-tensioning method, considering the overload vehicle moving at a speed of 60 km/h, based on the FEM calculation, the displacement time-history curves of the wing plate on the top section across the bridge of the 1/4, 1/2, and 3/4 sections are determined. The curve of vertical displacement change for each section over time is shown in Fig. 10.

Fig. 10Vertical displacement time-history curves at the side span

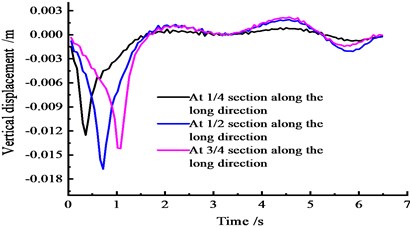
According to Fig. 10, under a moving load, the vertical displacement at the 1/4 section on the side span first reaches a peak, and then the subsequent peaks occur in sequence. The vertical displacement peak of the cross section reaches a maximum peak of 0.017 m. The peak of the vertical displacement in the 1/4 section is 0.012 m, and the vertical displacement peak of the 3/4 section is 0.014 m.

The acceleration time-history curves at the cross sections of 1/4, 1/2, and 3/4 are shown in Fig. 11.

Fig. 11Vertical acceleration time-history curves at the middle span

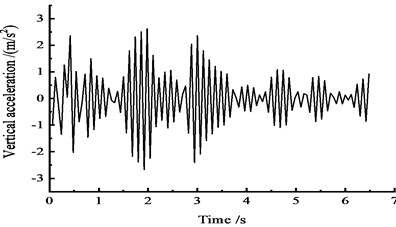
a) At the 1/4 section along the long direction

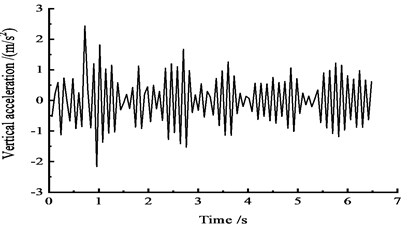
b) At the 1/2 section along the long direction

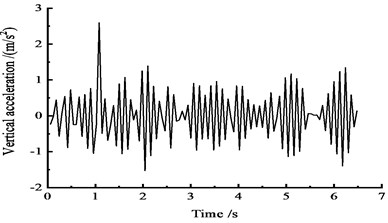
c) At the 3/4 section along the long direction

Fig. 11 shows that under the effect of a vehicle moving load, the peak vertical acceleration at the 1/4 section reaches 2.2 m/s² at approximately 2 s, the peak vertical acceleration at the 1/2 section reaches 2.0 m/s² at approximately 1 s, and the peak vertical acceleration at the 3/4 section reaches 2.3 m/s² at approximately 1 s.

(2) The middle span.

After reinforcement using the post-tensioning method, considering the overload vehicle moving at a speed of 60 km/h, based on the FEM calculation, the displacement time-history curves of the wing plate on the top section cross the bridge at the 1/4, 1/2, and 3/4 sections are determined. The vertical displacement curve of each section across the bridge when the vehicle moves across with the change in time is shown in Fig. 12.

Fig. 12Vertical displacement time-history curves at the middle span

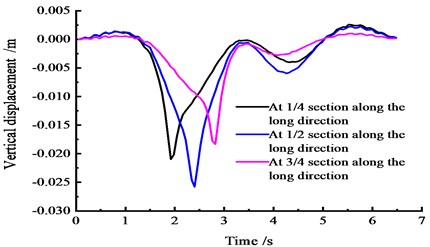
Fig. 12 shows that under a moving load, the vertical displacement at the 1/4 section on the side span first reaches a peak, and then the subsequent peaks arrive in sequence. The vertical displacement peak of the cross section reaches a maximum peak of 0.023 m. The peak of the vertical displacement in the 1/4 section is 0.017 m, the vertical displacement peak of the 3/4 section is 0.015 m, and the vertical displacement of each section is stable at 0-0.002 m.

The acceleration time-history curves at the 1/4, 1/2, and 3/4 cross sections of the middle span are shown in Fig. 13.

Fig. 13Vertical acceleration time-history curves at the middle span

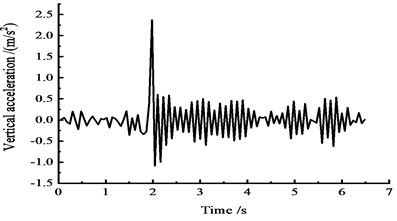
a) At the 1/4 section along the long direction

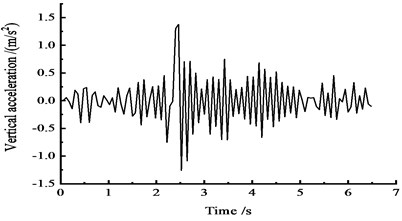
b) At the 1/2 section along the long direction

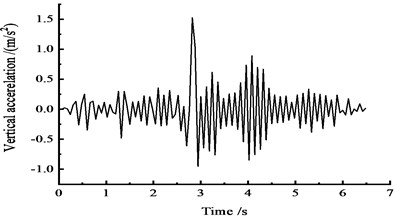
c) At the 3/4 section along the long direction

Fig. 13 shows that under the effect of a vehicle moving load, the vertical acceleration of the cross section reaches a peak: the peak vertical acceleration at the 1/4 section reaches 2.0 m/s² at approximately 2 s, the peak vertical acceleration at the 1/2 section reaches 1.3 m/s² at approximately 2.5 s, and the peak vertical acceleration at the 3/4 section reaches 1.4 m/s² at approximately 3 s.

4.2. Dynamic response of the overload 90-km/h vehicle-bridge coupling system

4.2.1. Coupled dynamic response of the box bridge before reinforcement

(1) The side span.

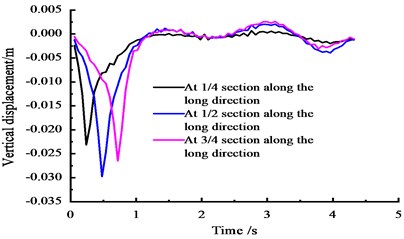
Considering the overload vehicle at a speed of 90 km/h, based on the FEM calculation, the displacement time-history curves of the wing plate on the top section across the bridge of the 1/4, 1/2, and 3/4 sections are obtained. The curve of the vertical displacement change of each section over time is shown in Fig. 14.

According to Fig. 14, under a moving load, the vertical displacement peak of the cross section reaches a maximum peak of 0.030 m and then gradually decreases forwards both ends. The peak of the vertical displacement in the 1/4 section is 0.023 m, the vertical displacement peak of the 3/4 section is 0.027 m, and the vertical displacement of each section is stable at 0-0.002 m.

Fig. 14Vertical displacement time-history curves at the middle span

The acceleration time-history curves at the 1/4, 1/2, and 3/4 sections are shown in Fig. 15.

Fig. 15Vertical acceleration time-history curves at the middle span

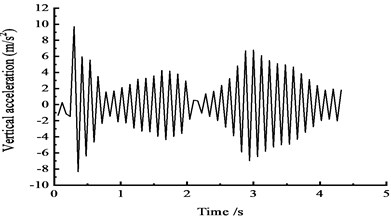
a) At the 1/4 section along the long direction

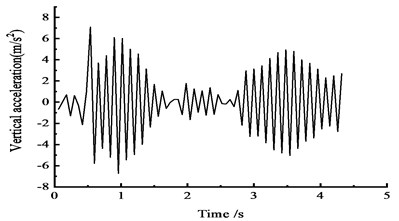
b) At the 1/2 section along the long direction

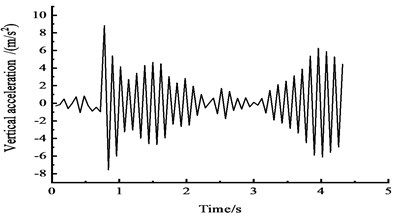
c) At the 3/4 section along the long direction

Fig. 15 shows that under the effect of a vehicle moving load, the peak vertical acceleration at the 1/4 section reaches 9.5 m/s² at approximately 0.5 s, the peak vertical acceleration at the 1/2 section reaches 7 m/s² at approximately 0.5 s, and the peak vertical acceleration at the 3/4 section reaches 9 m/s² at approximately 1 s.

(2) The middle span.

Considering the overload vehicle at a speed of 90 km/h, based on the FEM calculation, the displacement time-history curves of the wing plate on the top section across the bridge at the 1/4, 1/2, and 3/4 sections are obtained. The vertical displacement curve of each section across the bridge when the vehicle moves across with the change in time is shown in Fig. 16.

Fig. 16 shows that under a moving load, the vertical displacement peak of the cross section reaches the maximum peak of 0.037 m and gradually decreases forwards at both ends. The peak of the vertical displacement in the 1/4 section is 0.032 m, and the vertical displacement peak of the 3/4 section is 0.027 m.

The acceleration time-history curves at the 1/4, 1/2, and 3/4 cross sections of the middle span are shown in Fig. 17.

Fig. 16Vertical displacement time-history curves at the middle span

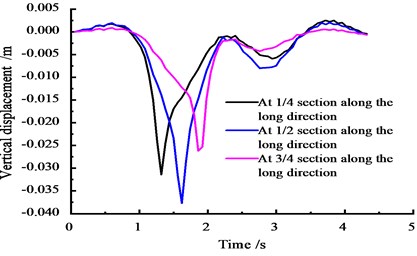
Fig. 17Vertical acceleration time-history curves at the middle span

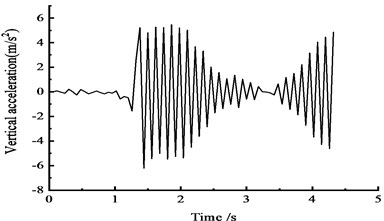
a) At the 1/4 section along the long direction

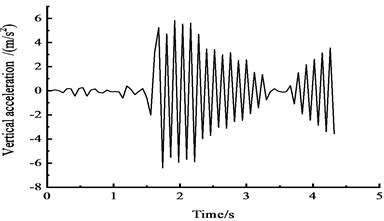
b) At the 1/2 section along the long direction

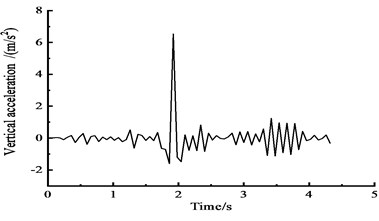
c) At the 3/4 section along the long direction

Fig. 17 shows that under the effect of a vehicle moving load, the peak vertical acceleration at the 1/4 section reaches 6.2 m/s² at approximately 1.5 s, the peak vertical acceleration at the 1/2 section reaches 6.5 m/s² at approximately 2 s, and the peak vertical acceleration at the 3/4 section reaches 6.8 m/s² at approximately 2 s.

4.2.2. Coupling dynamic response of the post-tensioning box bridge after reinforcement

(1) The side span.

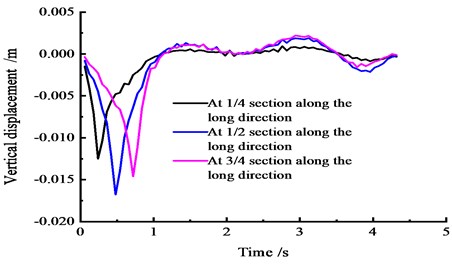
After the reinforcement of the post-tensioning method and the overloading of vehicles at a speed of 90 km/h and based on the FEM calculation, the curves of the side span at the 1/4, 1/2, and 3/4 sections on the top section of the wing plate displacement are obtained; the curve of each section in the vehicle bridge vertical displacement variation with time is shown in Fig. 18.

Fig. 18 shows that under a vehicle moving load, the vertical displacement peak at the cross section reaches 0.017 m and gradually decreases to both ends, where the vertical displacement of the 1/4 section is 0.013 m, and the peak vertical displacement of the 3/4 section is 0.015 m.

Fig. 18Vertical displacement time-history curves at the side span

The acceleration time-history curves at the cross sections of 1/4, 1/2, and 3/4 are shown in Fig. 19.

Fig. 19Vertical acceleration time-history curves at the side span

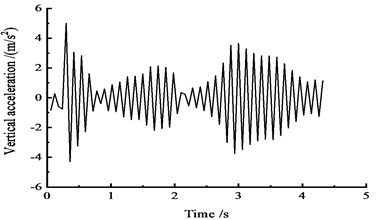
a) At the 1/4 section along the long direction

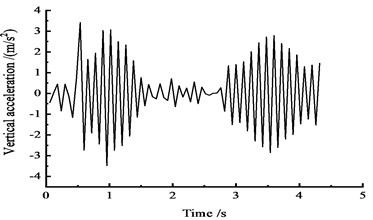
b) At the 1/2 section along the long direction

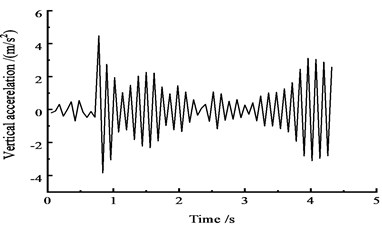
c) At the 3/4 section along the long direction

Fig. 19 shows that under the effect of a vehicle moving load, the peak vertical acceleration of the cross section at the edge of the 1/4 section reaches 5 m/s² at approximately 0.5 s, the peak vertical acceleration at the 1/2 section reaches 3.6 m/s² at approximately 0.5 s, and the vertical acceleration peak reaches 4.2 m/s² at the 3/4 section at approximately 1 s.

(2) The middle span.

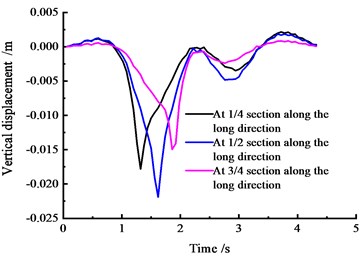
After the reinforcement of the post-tensioning method, according to the FEM curves of the 1/4, 1/2, and 3/4 sections, at the cross section of the top wing plate displacement, the vertical sections in the vehicle bridge displacement time curves are calculated, as shown in Fig. 20.

According to Fig. 20, under the moving vehicle load, the mid-span cross section vertical displacement peak value is achieved at 0.022 m and gradually decreases to both sides; in the 1/4 section, the vertical displacement peak value is 0.017 m, and in the 3/4 section, the vertical displacement peak value is 0.015 m.

Fig. 20Vertical displacement time-history curves at the middle span

The acceleration time history curves at the 1/4, 1/2, and 3/4 cross sections of the middle span are selected, as shown in Fig. 21.

Fig. 21Vertical acceleration time-history curves at the middle span

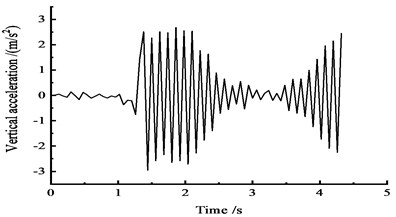
a) At the 1/4 section along the long direction

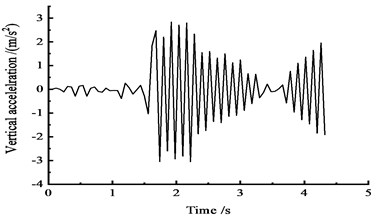
b) At the 1/2 section along the long direction

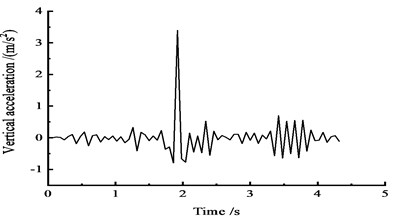
c) At the 3/4 section along the long direction

Fig. 21. shows that, under the effect of a vehicle moving load, the peak vertical acceleration is 2.9 m/s² in the 1/4 cross section at approximately 1.5 s, the peak vertical acceleration of the 1/2 section is 3.1 m/s² at approximately 2 s, and the vertical acceleration peak value appeared in the 3/4 section is 3.5 m/s² at approximately 2 s.

5. Conclusions

With the increase in vehicle speed, the vertical displacement of the bridge has almost no change, but the increase in the peak value of vertical acceleration is obvious, which results in a faster arrival of the vertical displacement and the vertical acceleration peak value and also causes the amplitude of the vertical acceleration of the bridge to increase greatly. Through comparative analysis, it is found that the vertical acceleration increase in the side span is significantly larger than that in the middle span.

Through the comparative analysis of the dynamic response of a bridge under the same moving load before and after reinforcement, it is found that the post-tensioned CFRP reinforcement method can effectively reduce the vertical displacement and acceleration of the bridge, but the vertical displacement increment of the post-tensioned CFRP reinforcement method is almost the same with different vehicle speeds, and the vertical acceleration increment of the bridge decreases with speed. The increase shows that the post-tensioned prestressed CFRP reinforcement has some shortcomings in reducing the vertical displacement of the bridge.

From the point of view of the amplitude of the acceleration time history analysis curves, with the increase in velocity, the amplitude increment of vertical acceleration of the middle span is significantly smaller than that of the side span. With the increase in speed, the effect of the post-tensioned method is better.

As the carbon fiber cloth is exposed to the outside for a long time, it is easy to be damaged, but this paper does not mention the treatment of carbon fiber cloth fire-proof and anti-corrosion, so it is necessary to further study the fire-proof and anti-corrosion of carbon fiber cloth. At the same time, the effect of the number and spacing of CFRP sheets on post-tensioned reinforcement is not considered in this reinforcement project, which also needs to be studied.